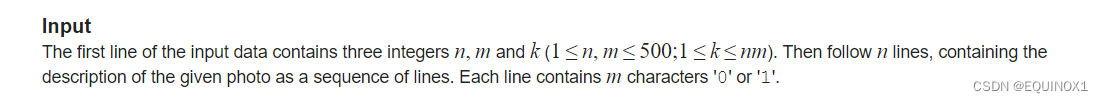前缀和+双指针,CF 131F - Present to Mom
一、题目
1、题目描述
2、输入输出
2.1输入
2.2输出
3、原题链接
131F - Present to Mom
二、解题报告
1、思路分析
很经典的一种把列看作cell 来进行双指针/递推的题型
我们考虑,可以预处理出原矩阵中的所有star
然后我们去枚举矩形的上下边界,把边界内的每列当成一个格子的话,问题就变成了求和至少大于等于k的子数组的数目
这个经典问题我们双指针可以搞定
而快速计算列和可以预处理前缀和
2、复杂度
时间复杂度: O(n^2m)空间复杂度:O(nm)
3、代码详解
#include <bits/stdc++.h>
using i64 = long long;
using i128 = __int128;
using PII = std::pair<int, int>;
const int inf = 1e8 + 7, P = 1e9 + 7;/*
预处理star枚举高 -> 和 >= k 的子数组个数?
two pointers
*/void solve() {int n, m, k;std::cin >> n >> m >> k;std::vector<std::string> g(n);for (int i = 0; i < n; i ++ ) std::cin >> g[i];std::vector<std::vector<int>> f(n, std::vector<int> (m));std::array<int, 5> dir { 1, 0, -1, 0, 1 };for (int i = 1; i + 1 < n; i ++ )for (int j = 1; j + 1 < m; j ++ ) {if (g[i][j] == '1') {bool flag = true;for (int k = 0; k < 4; k ++ )if (g[i + dir[k]][j + dir[k + 1]] == '0')flag = false;f[i][j] = flag; }}std::vector<std::vector<int>> pre(f);for (int i = 1; i < n; i ++ )for (int j = 0; j < m; j ++ )pre[i][j] += pre[i - 1][j];i64 res = 0;for (int lo = 0; lo < n; lo ++ ) {for (int hi = lo + 2; hi < n; hi ++ ) {int l = 1, r = 1, cur = 0;while (l + 1 < m) {while (r + 1 < m && cur < k)cur += pre[hi - 1][r] - pre[lo][r], ++ r;if (cur < k) break;res += (m - r);cur -= pre[hi - 1][l] - pre[lo][l];++ l;}}}std::cout << res;
}int main(int argc, char** argv) {std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);int _ = 1;// std::cin >> _;while (_ --)solve();return 0;
}相关文章:

前缀和+双指针,CF 131F - Present to Mom
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 131F - Present to Mom 二、解题报告 1、思路分析 很经典的一种把列看作cell 来进行双指针/递推的题型 我们考虑,可以预处理出原矩阵中的所有star 然后我们去枚举矩形的上下边界,把…...
HCIA-速查-ENSP模拟器2步清空配置
需求:清空模拟器配置 清空当前图中配置 步骤1:reset saved-configuration 后输入y确认 步骤2:reboot后输入n否认再输入y确认 验证已经清空配置...

优选算法刷题笔记 2024.6.10-24.6.20
一、双指针算法(快慢指针,对撞指针) 艹,CSDN吞了我是十三题笔记!!! 二、滑动窗口(滑动窗口) 1、找到字符串中所有字母异位词 class Solution {public List<Integer> findAnagrams(String s, String p) {int[] hash1 new in…...
无需科学上网:轻松实现国内使用Coze.com平台自己创建的Bot(如何实现国内免费使用GPT-4o/Gemini等最新大模型)
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 如何在国内使用 Coze.com 创建的 Bot 📒📝 创建Bot📝 实现国内使用📝 测试⚓️ 相关链接 ⚓️📖 介绍 📖 Coze.com 是一个强大的平台,允许用户创建各种类型的 Bot。然而,许多国内用户可能会遇到访问问题,导致无法…...
【车载开发系列】CAN通信总线再理解(中篇)
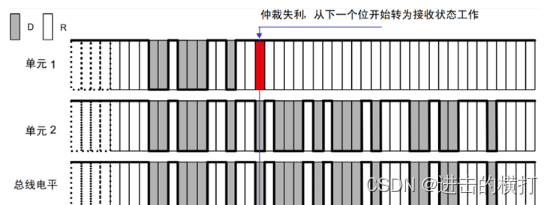
【车载开发系列】CAN通信总线再理解(中篇) 九. CAN总线标准十. CAN物理层十一. CAN数据链路层1)CAN的通信帧类型2)CAN的标准帧格式1. CAN ID2. 数据场 3)CAN总线仲裁 十二. CAN应用层1)CANopen2)…...

系统编程:互斥锁,条件变量
互斥锁 使用过程: 1,声明锁: pthread_mutex_t lock; 2,初始化锁:pthread_mutex_init(&lock,NULL); 3,在线程的方法函数中上锁和解锁:(成对出现) pthread_mutex_lock(&lock); pthread_mutex_unlock(&lock); 4,销毁锁:pthread_mutex_destroy(&lock); 代码示例:…...

蓝鹏测控公司全长直线度算法项目多部门现场组织验收
关键字:全场直线度算法,直线度测量仪,直线度检测,直线度测量设备, 6月18日上午,蓝鹏测控公司全长直线度算法项目顺利通过多部门现场验收。该项目由公司技术部、开发部、生产部等多个部门共同参与,旨在提高直线度测量精度,满足高精度制造领域需…...

使用Python进行音频处理
通常会使用wave模块。但是,如果您想要处理其他类型的音频文件,或者需要更高级的音频处理功能,您可能需要安装第三方库,如pydub、soundfile、numpy等。 import wave # 读取WAV文件 with wave.open(input.wav, rb) as wav_file: …...

家有老人小孩,室内灰尘危害大!资深家政教你选对除尘空气净化器
哈喽,各位亲爱的朋友们!今天我们来聊聊每次大扫除时最让人头疼的问题——灰尘。你有没有发现,两天不打扫,桌子上就能积上一层灰;阳光一照,地板上的灰尘都在跳舞;整理被子的时候,空气…...

AI在创造与毁灭之间摇摆:音乐产业的机遇与挑战并存
AI到底在创造还是毁掉音乐? 最近一个月,轮番上线的音乐大模型,一举将素人生产音乐的门槛降到了最低,并掀起了音乐圈会不会被AI彻底颠覆的讨论。短暂的兴奋后,AI产品的版权归属于谁,创意产业要如何在AI的阴…...

Spring Boot集成 Spring Retry 实现容错重试机制并附源码
😄 19年之后由于某些原因断更了三年,23年重新扬帆起航,推出更多优质博文,希望大家多多支持~ 🌷 古之立大事者,不惟有超世之才,亦必有坚忍不拔之志 🎐 个人CSND主页——Mi…...
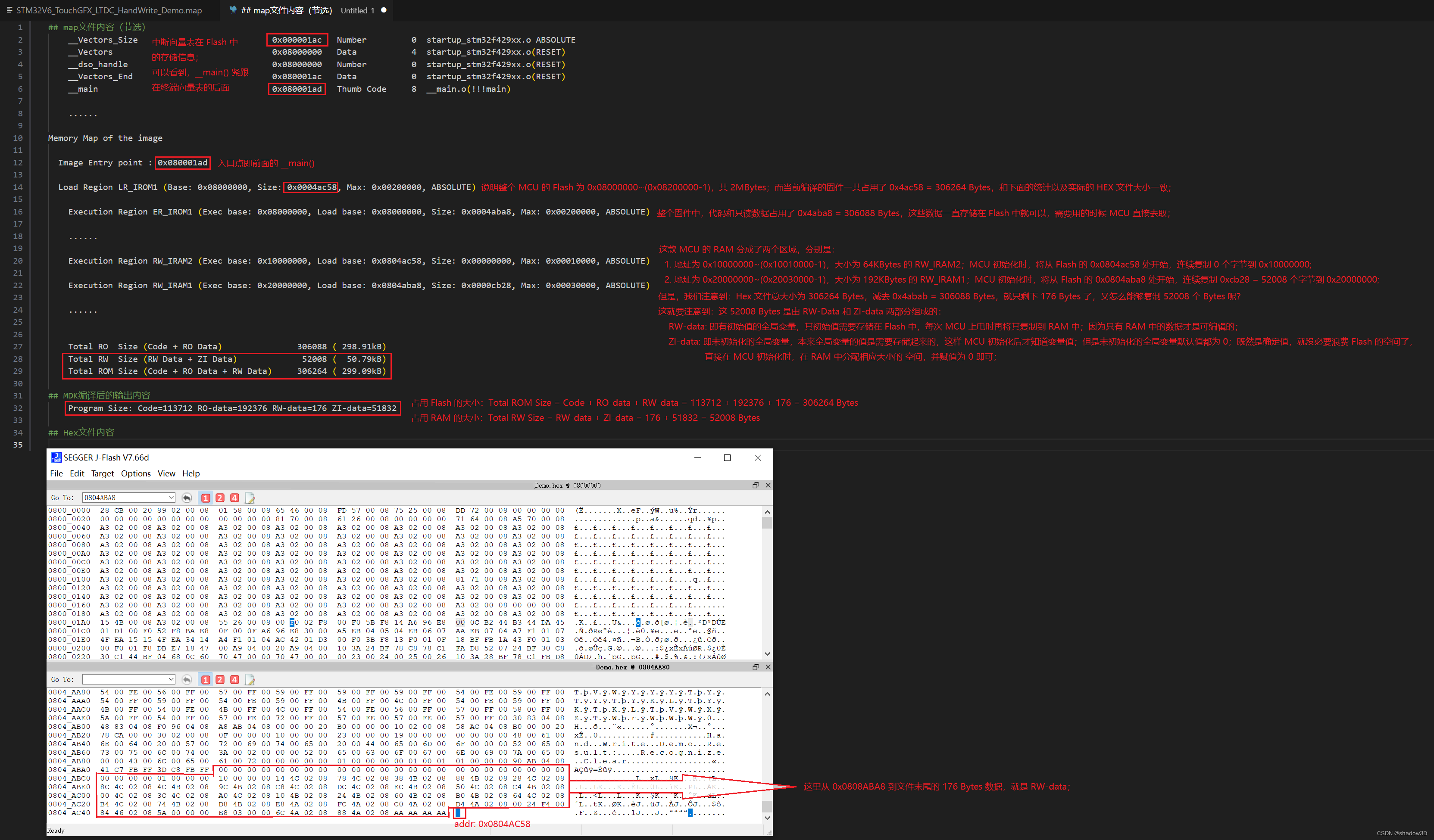
MDK-ARM 编译后 MAP 文件分析
本文配合 STM32 堆栈空间分布 食用更佳! 一图胜千言。。。...

antv g6实现系统拓扑图
1 背景 为例描述各个服务、redis、mysql等之间的联系及其健康状态,构建系统拓扑图,考虑 g6 更适合处理大量数据之间的关系,所以我们采用g6来绘制前端的图形。 g6提供的支持: 节点/边类型多样,同样支持自定义对于节点…...

因路径规划异常导致导航停止 Failed to pass global plan to the controller
因路径规划异常导致导航停止 Failed to pass global plan to the controller 控制台错误信息: [ WARN] [1718875656.343893537, 93.698000000]: Transformed plan is empty. Aborting local planner! [ERROR] [1718875656.343922719, 93.698000000]: move_base.cpp:854 Faile…...

AOSP开发环境搭建
目录 一、安装虚拟机 二、安装Ubuntu 三、安装VMware tools 3.1、通用安装 3.2、Ubuntu22.04 中Drag and drop is not supported问题 四、安装依赖环境 4.1、安装git 4.2、下载Python3 4.3、解压Python3 4.4、编译与安装Python3 3.sudo make install 4.5、安装Pyth…...

React native新架构组成
React Native 的新架构(New Architecture)引入了一些新的组件和概念,旨在提高性能、增强灵活性和简化跨平台开发。主要组成部分包括: Fabric: Fabric Renderer: Fabric 是新的渲染引擎,它旨在取代现有的渲染引擎。与…...

Spring Security+Spring Boot实现登录认证以及权限认证
基本概念 “Authentication(认证)”是spring security框架中最重要的功能之一,所谓认证,就是对当前访问系统的用户给予一个合法的身份标识,用户只有通过认证才可以进入系统,在物理世界里,有点类似于“拿工卡刷门禁”的…...

5款堪称变态的AI神器,焊死在电脑上永不删除!
一 、AI视频合成工具——Runway: 第一款RunWay,你只需要轻轻一抹,视频中的元素就会被擦除,再来轻轻一抹,直接擦除,不喜欢这个人直接擦除,一点痕迹都看不出来。 除了视频擦除功能外,…...

Python和OpenCV图像分块之图像边长缩小比率是2
import cv2 import numpy as npimg cv2.imread("F:\\mytupian\\xihuduanqiao.jpg") # 低反光 cv2.imshow(image, img) # # 图像分块 # dst np.zeros(img.shape, img.dtype) ratio 2 #图像边长缩小比率是2,也就是一张图片被分割成四份 height, wi…...
是什么,以及它的用途和优缺点)
C语言中的位域(bit-field)是什么,以及它的用途和优缺点
在C语言中,位域(bit-field)是一种特殊的数据结构,它允许在结构体(struct)中定义其成员所占用的位数,而不是使用整个字节或更大的内存空间。位域通常用于存储布尔值、状态标志、硬件控制位等&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...