云服务器部署Neo4j
文章目录
- 导读
- 安装Neo4j
- 先去官网看看
- 下载安装包
- 如果真的下载了rpm安装包
- 插件
导读
大模型,他终于来了。
不过呢,大模型相关,现在也就跟着热点去尝试一下multi-agent的RAG方向,看看能做到什么地步。总之我们先从安装neo4j开始。
安装Neo4j
先去官网看看
要说到知识图谱的话,那就必然是Neo4j了。我们直接点击这里跳转到官方下载页。
P.S.:比较好玩的是,人家的官网下载中心并不是什么
download,而是deployment center。
看起来很正常。
下载安装包
如果说要下载什么,我相信你第一眼看到的绝对是这个。

当然啦,如果是Windows的话,你当然没得选,只能点击这个。
那么,Linux呢?也是选择rpm嘛?
也可以。但是呢,如果使用rpm或者deb包的话,后续安装过程中解决依赖是一个相当麻烦的事情。如果说,有这么一个能够完美解决所有依赖的源,那就太棒了。
所以,我们其实还有更方便的选择:

点击Visit,人家就已经清晰地告诉你要怎么做了:
首先,我们需要导入签名密钥:
$ sudo rpm --import https://debian.neo4j.com/neotechnology.gpg.key
就跟apt一样,导入key,才能够验证包。
然后呢,为了避免升级,我们需要指定一个yum源。人家也非常贴心地给了我们一些例子,这里我就不全部放出来了。我使用的是第5代的产品,所以这里给出第5代的案例:
# Neo4j 5
cat <<EOF> /etc/yum.repos.d/neo4j.repo
[neo4j]
name=Neo4j Yum Repo
baseurl=https://yum.neo4j.com/stable/5
enabled=1
gpgcheck=1
EOF
这一段怎么使用呢?如果你熟悉Linux命令,那就是直接从cat开始复制,到第二个EOF为止。如果你并不太熟悉cat有这样的作用,那就用echo老实处理:
echo "[neo4j]
name=Neo4j Yum Repo
baseurl=https://yum.neo4j.com/stable/5
enabled=1
gpgcheck=1
EOF" > /etc/yum.repos.d/neo4j.repo
P.S.:如果直接复制上面这一段,是会默认加上换行,所以不需要额外加上
\n。而如果你运气不太好,只能使用手打,就需要加\n了。
完事儿了,我们更新一下:
$ sudo yum update
然后呢,我们来安装一下:
$ sudo yum install neo4j
这个时候,linux就会很贴心的帮我们解决依赖问题。
如果真的下载了rpm安装包
而如果在最开始的时候,你选择了rpm或者deb包,那么安装就会报错,要求你优先安装java-17、cypher-shell这俩玩意。
如果你不小心下载了rpm包(假设你是AlmaLinux9),该怎么办呢?
首先,java-17很好找。
$ sudo dnf install java-17-openjdk
需要注意的是,这个还不能使用我们寻常配置jdk环境变量一样的过程,因为neo4j依赖了jdk以及jre。jre是我们在配置环境过程中基本不会去考虑的一个小东西,不太熟悉的话也千万不要乱安装,容易把各种东西弄得乱七八糟。
然后,在官方下载页,我们还需要额外下载cypher-shell,也是下载rpm包到本地。
然后,一步步来:
$ sudo rpm -ivh cypher-shell-${你下载的版本}.noarch.rpm
$ sudo rpm -ivh neo4j-${你下载的版本}.noarch.rpm
然后,就可以看看是不是成了:
$ neo4j version
或者直接启动一下:
$ neo4j console
因为我目前发现fedora安装第4代neo4j的时候会崩溃,所以需要使用console运行大约15秒左右,才能够保证没什么问题。
插件
Neo4j的插件已经算是相当友好的了。我们只需要找到neo4j的插件,然后放入插件保存位置就好了。
P.S.:插件的默认保存位置在/var/lib/neo4j/plugins。
然而,插件并不是这么好找。我们最终在这个地方找到了插件,点击这里就能跳转到下载页
需要注意的是,官网里面提到,需要neo4j的版本号的前两位数字与apoc的版本号的前两位数字严格一致。也就是说,我下载的最新版是5.20.0,那么apoc的版本号应该是5.20.0。如果neo4j的版本更新到了5.20.1,那么apoc的版本可以不做更改,因为5跟20都是一样的。但是如果neo4j更新到了5.21.0,那么apoc的版本号应该改为5.21.0。
github的东西并不能非常方便地用wget请求到,所以只能手动下载后scp传上去。
插件放在/var/lib/neo4j/plugins下,然后重启一下neo4j:
$ neo4j restart
就可以访问了。
相关文章:

云服务器部署Neo4j
文章目录 导读安装Neo4j先去官网看看下载安装包如果真的下载了rpm安装包 插件 导读 大模型,他终于来了。 不过呢,大模型相关,现在也就跟着热点去尝试一下multi-agent的RAG方向,看看能做到什么地步。总之我们先从安装neo4j开始。…...

day64 图论 图论理论基础 深搜 广搜 98. 所有可达路径
图论理论基础 图的种类 整体上一般分为 有向图 和 无向图。 度 无向图中有几条边连接该节点,该节点就有几度。 在有向图中,每个节点有出度和入度。 出度:从该节点出发的边的个数。 入度:指向该节点边的个数。 连通性 在图…...
从0进入微服务需要了解的基础知识
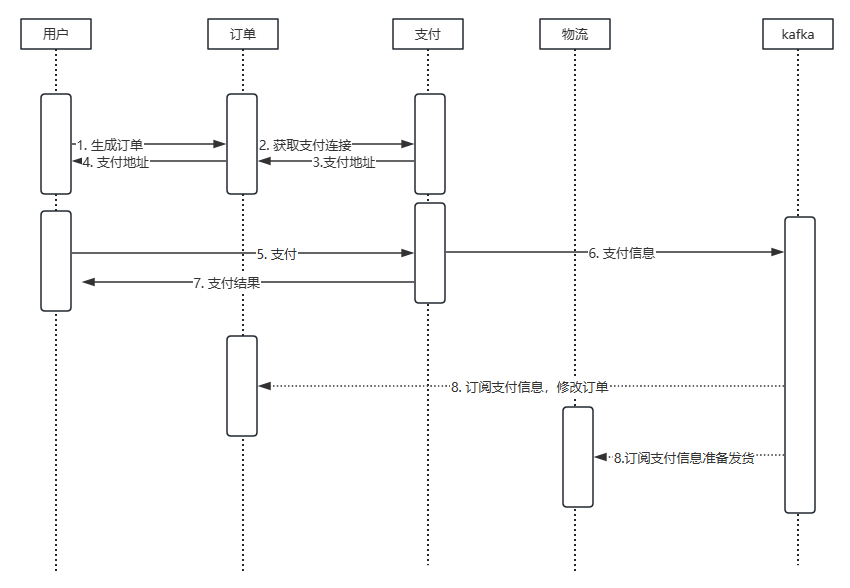
文章目录 系统架构演化过程为什么要了解系统架构的演化过程技术发展认知技术选型与创新 演变过程单体架构分层-分布式集群微服务 分布式\集群\微服务 微服务中的核心要素-拆分原则项目拆分与复杂度微服务的拆分维度有哪些小结 微服务中的核心要素服务化进行拆分后一定是微服务&…...

MySQL之复制(七)
复制 定制的复制方案 分离功能 许多应用都混合了在线事务处理(OLTP)和在线数据分析(OLAP)的查询。OLTP查询比较短并且是事务型的。OLAP查询则通常很大,也很慢,并且不要求绝对最新的数据。这两种查询给服务器带来的负担完全不同,因此它们需…...

Redis分片集群搭建
主从模式可以解决高可用、高并发读的问题。但依然有两个问题没有解决: 海量数据存储高并发写 要解决这两个问题就需要用到分片集群了。分片的意思,就是把数据拆分存储到不同节点,这样整个集群的存储数据量就更大了。 Redis分片集群的结构如…...

请解释Java中的策略模式,并举例说明其应用场景和实现方式。请解释Java中的模板方法模式,并讨论其在实际项目中的应用。
请解释Java中的策略模式,并举例说明其应用场景和实现方式。 策略模式(Strategy Pattern) 策略模式是一种行为设计模式,它使你能够定义一系列算法,并将每一个算法封装起来,使它们可以互相替换。策略模式使…...
Vim基础操作:常用命令、安装插件、在VS Code中使用Vim及解决Vim编辑键盘错乱
Vim模式 普通模式(Normal Mode): 这是 Vim 的默认模式,用于执行文本编辑命令,如复制、粘贴、删除等。在此模式下,你可以使用各种 Vim 命令来操作文本。插入模式(Insert Mode)&#…...

基于Windows API DialogBox的对话框
在C中,DialogBox函数是Windows API的一部分,它用于在Win32应用程序中创建并显示一个模态对话框。DialogBox函数是USER32.DLL中的一个导出函数,因此你需要在你的C Win32应用程序中链接到这个库。 #include "framework.h" #include …...

五十一、openlayers官网示例Layer Min/Max Resolution解析——设置图层最大分辨率,超过最大值换另一个图层显示
使用minResolution、maxResolution分辨率来设置图层显示最大分辨率。 <template><div class"box"><h1>Layer Min/Max Resolution</h1><div id"map" class"map"></div></div> </template><…...

24年计算机等级考试22个常见问题解答❗
24年9月计算机等级考试即将开始,整理了报名中容易遇到的22个问题,大家对照入座,避免遇到了不知道怎么办? 1、报名条件 2、报名入口 3、考生报名之后后悔了,不想考了,能否退费? 4、最多能够报多少…...

obsidian制作自己的主题一文入门
制作自己的主题 我最近发现一款插件,直接把obsidian的文章格式复制到公众号中。 我非常喜欢这个功能,这将减少公众号排版的时间,同时保持公众号文章格式的一致性。 但是这个插件提供的模板不能满足我的需求,所以,需要…...

游戏心理学Day20
扩展的8种玩家 完成主义者 此类玩家关心的是成就和进展,其主要目的是完成游戏的主要目标,其次是完成游戏的次要目标之后才是游戏中的其他内容,在多人游戏中完成主义者会致力于炫耀自己的状态和财富。如果游戏以胜负为目标,那么此…...

Serverless如何赋能餐饮行业数字化?乐凯撒思变之道
导语 | 在数字化浪潮席卷全球的今天,每一个行业都在经历着前所未有的变革。餐饮行业作为人们日常生活中不可或缺的一部分,更是面临着巨大的转型压力。如何完成数字化转型,打破传统经营模式的限制,成为摆在众多餐饮商家面前的一道难…...

css系列:音频播放效果-波纹律动
介绍 语音播放的律动效果,通俗来说就是一个带动画的特殊样式的进度条,播放的部分带有上下律动的动画,未播放的部分是普通的灰色竖状条。 实现中夹带了less变量、继承和循环遍历,可以顺带学习一下。 结果展示 大致效果如图所示…...

WPF学习(1)--类与类的继承
在面向对象编程中,继承是一种机制,允许一个类(称为子类或派生类)从另一个类(称为父类或基类)继承属性和方法。继承使我们能够创建一个通用类,然后根据需要扩展或修改它以创建更具体的类。以下是…...
)
Spring Boot框架的原理及应用详解(六)
本系列文章简介: 在当今的软件开发世界中,快速迭代、高效开发以及易于维护成为了开发者们不断追求的目标。Spring Boot作为Spring框架的一个子项目,自其诞生以来就凭借其“约定大于配置”的理念和自动配置的特性,迅速在Java开发社…...
)
密码学与信息安全面试题及参考答案(2万字长文)
目录 什么是密码学?它的主要目标是什么? 请解释明文、密文、加密和解密的概念。 密码系统的安全性通常基于哪三种假设? 什么是Kerckhoffs原则?它对现代密码学设计有何意义? 简述密码学中的“混淆”和“扩散”概念。 什么是AES(高级加密标准)?AES有几种常见的密钥…...
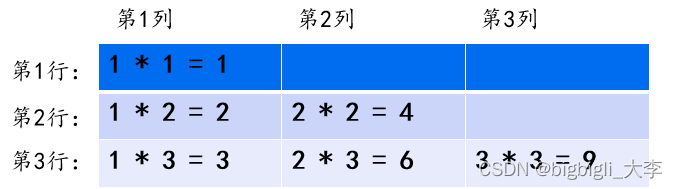
C++语法19 循环嵌套结构(for/while循环)
语法阶段已经更新到第18章了,前面的知识你都学会了吗?如果还没有学习前面的知识,请点击👉语法专栏进行学习哦! 目录 循环嵌套 训练:数字矩形 解析 参考代码 训练:星号三角形 解析 参考代码 …...

AtomicInteger原理和CAS与Synchronized(juc编程)
AtomicInteger原理 4.6.1 原理介绍 AtomicInteger的本质:自旋锁 CAS算法 CAS的全成是: Compare And Swap(比较再交换); 是现代CPU广泛支持的一种对内存中的共享数据进行操作的一种特殊指令。CAS可以将read-modify-write转换为原子操作,这…...

抖音a_bogus,mstoken全参数爬虫逆向补环境2024-06-15最新版
抖音a_bogus,mstoken全参数爬虫逆向补环境2024-06-15最新版 接口及参数 打开网页版抖音,右键视频进入详情页。F12打开控制台筛选detail,然后刷新网页,找到请求。可以发现我们本次的参数目标a_bogus。a_bogus有时长度为168有时为172…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement
Cilium动手实验室: 精通之旅---13.Cilium LoadBalancer IPAM and L2 Service Announcement 1. LAB环境2. L2公告策略2.1 部署Death Star2.2 访问服务2.3 部署L2公告策略2.4 服务宣告 3. 可视化 ARP 流量3.1 部署新服务3.2 准备可视化3.3 再次请求 4. 自动IPAM4.1 IPAM Pool4.2 …...

使用SSE解决获取状态不一致问题
使用SSE解决获取状态不一致问题 1. 问题描述2. SSE介绍2.1 SSE 的工作原理2.2 SSE 的事件格式规范2.3 SSE与其他技术对比2.4 SSE 的优缺点 3. 实战代码 1. 问题描述 目前做的一个功能是上传多个文件,这个上传文件是整体功能的一部分,文件在上传的过程中…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...
