LeetCode-面试题 17.05. 字母与数字【前缀和,哈希表】
LeetCode-面试题 17.05. 字母与数字【前缀和,哈希表】
- 题目描述:
- 解题思路一:前缀和。数字为-1,字母为1。我们需要找到的子数组是前缀和之差为0的,例如s[right]-s[left]=0,那么s[right]=s[left],变为找前缀和相同的了。我们用一个字典记录前缀和的最早出现下标。
- 解题思路二:用一个整数替换前缀和列表,在遍历array过程中计算前缀和。其值在[-n,n]之间故数组长设为2n+1。具体看注释。
- 解题思路三:0
题目描述:
给定一个放有字母和数字的数组,找到最长的子数组,且包含的字母和数字的个数相同。
返回该子数组,若存在多个最长子数组,返回左端点下标值最小的子数组。若不存在这样的数组,返回一个空数组。
示例 1:
输入: [“A”,“1”,“B”,“C”,“D”,“2”,“3”,“4”,“E”,“5”,“F”,“G”,“6”,“7”,“H”,“I”,“J”,“K”,“L”,“M”]
输出: [“A”,“1”,“B”,“C”,“D”,“2”,“3”,“4”,“E”,“5”,“F”,“G”,“6”,“7”]
示例 2:
输入: [“A”,“A”]
输出: []
提示:
array.length <= 100000
https://leetcode.cn/problems/find-longest-subarray-lcci/description/
解题思路一:前缀和。数字为-1,字母为1。我们需要找到的子数组是前缀和之差为0的,例如s[right]-s[left]=0,那么s[right]=s[left],变为找前缀和相同的了。我们用一个字典记录前缀和的最早出现下标。
array.length 非常大,常规暴力算法难以不超时。
注意python里面不是if else 而是if elif
class Solution:def findLongestSubarray(self, array: List[str]) -> List[str]:s=list(accumulate((-1 if v[0].isdigit() else 1 for v in array),initial=0))left=right=0#前缀和一般是左闭右开[left,right)first={}#记录前缀和最早出现的下标for i,v in enumerate(s):j=first.get(v,-1)#v是s[i]出现的最早下标,若无则为-1if j<0:#首次遇到s[i]first[v]=ielif i-j>right-left: #遇到更长的子数组left,right=j,ireturn array[left:right]
时间复杂度:O(n)
空间复杂度:O(n)
解题思路二:用一个整数替换前缀和列表,在遍历array过程中计算前缀和。其值在[-n,n]之间故数组长设为2n+1。具体看注释。
class Solution:def findLongestSubarray(self, array: List[str]) -> List[str]:left=right=0#前缀和一般是左闭右开[left,right)s=n=len(array)#s初始化为n防止出现负数下标first=[-1]*(2*n+1)#记录前缀和最早出现的下标,初始化为-1长为2n+1的数组first[s]=0#s[0]=0for i,v in enumerate(array,1):#表示i从1开始计数s+=-1 if v[0].isdigit() else 1j=first[s] #first[s]是s[i]出现的最早下标,若无则为-1if j<0:#首次遇到s[i]first[s]=ielif i-j>right-left: #遇到更长的子数组left,right=j,ireturn array[left:right]
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
相关文章:

LeetCode-面试题 17.05. 字母与数字【前缀和,哈希表】
LeetCode-面试题 17.05. 字母与数字【前缀和,哈希表】题目描述:解题思路一:前缀和。数字为-1,字母为1。我们需要找到的子数组是前缀和之差为0的,例如s[right]-s[left]0,那么s[right]s[left],变为…...
| 机考必刷)
华为OD机试题 - 叠放书籍(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:叠放书籍题目输入输出示例一输入输出Code解题思路版权说明华为O…...

【数据库概论】第十一章 数据库并发控制
第十一章 并发控制 在多处理机系统中,每个处理机可以运行一个事务,多个处理机可以同时运行多个事务,实现多个事务并行运行,这就是同时并发方式。当多个用户并发存取数据库时会产生多个事务同时存取同一事务的情况,如果…...
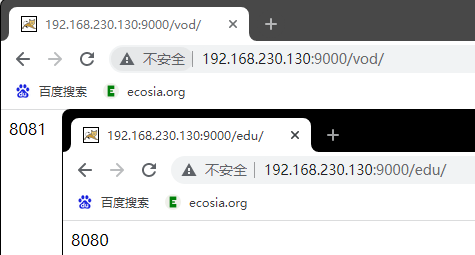
Nginx配置实例-反向代理案例二
实现效果:使用nginx反向代理,根据访问的路径跳转到不同端口服务 nginx监听端口为9000, 访问 http://127.0.0.1:9000/edu/ 直接跳转到127.0.0.1:8080 访问 http://127.0.0.1:9000/vod/ 直接跳转到127.0.0.1:8081 一、准备工作 1. 准备两个tom…...

HTML 字符集
为了正确显示 HTML 页面,Web 浏览器必须知道要使用哪个字符集。 从 ASCII 到 UTF-8 ASCII 是第一个字符编码标准。ASCII 定义了 128 种可以在互联网上使用的字符:数字(0-9)、英文字母(A-Z)和一些特殊字符…...

【C语言】每日刷题 —— 牛客语法篇(3)
前言 大家好,继续更新专栏c_牛客,不出意外的话每天更新十道题,难度也是从易到难,自己复习的同时也希望能帮助到大家,题目答案会根据我所学到的知识提供最优解。 🏡个人主页:悲伤的猪大肠9的博客…...
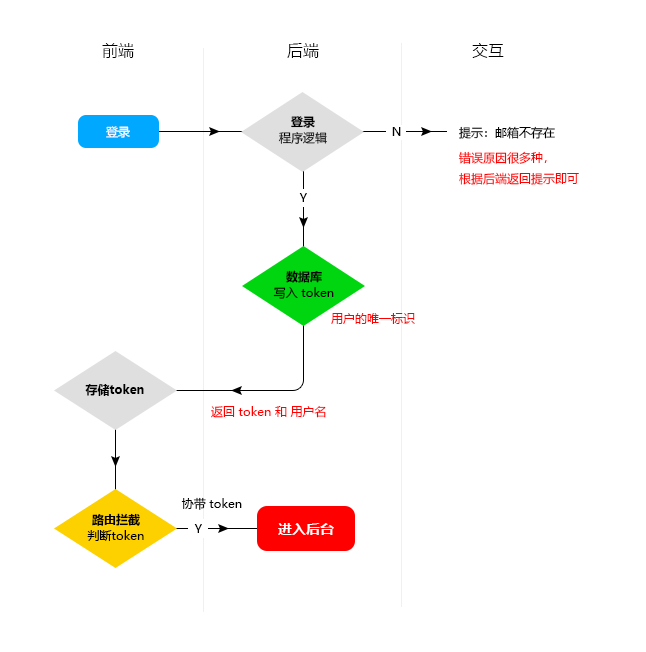
基于Vue3和element-plus实现一个完整的登录功能
先看一下最终要实现的效果:登录页面:注册页面:(1)引入element-plus组件库引入组件库的方式有好多种,在这里我就在main.js全局引入了.npm i element-plus -Smain.js中代码:import { createApp } from "vue"; //element-plus import ElementPlus from "element-pl…...

【java】Java 中泛型的实现原理
文章目录前序1. 泛型1.1 泛型方法1.2 泛型类1.3 泛型接口2. 泛型的基本原理3. 小结前序 泛型是 Java 开发中常用的技术,了解泛型的几种形式和实现泛型的基本原理,有助于写出更优质的代码。本文总结了 Java 泛型的三种形式以及泛型实现原理。 1. 泛型 …...
)
【C++提高编程】C++全栈体系(二十七)
C提高编程 第五章 STL- 常用算法 三、常用排序算法 算法简介: sort //对容器内元素进行排序random_shuffle //洗牌 指定范围内的元素随机调整次序merge // 容器元素合并,并存储到另一容器中reverse // 反转指定范围的元素 1. sort 功能描述&#…...

软考高级信息系统项目管理师系列之三十九:项目集管理
软考高级信息系统项目管理师系列之三十九:项目集管理 一、项目集管理内容二、项目集管理基础概述1.项目集定义2.项目集活动3.项目集管理三、项目集的管理过程四、项目集治理1.项目集治理概述2.项目集指导委员会的职责3.项目集治理功能五、项目集生命周期1.项目集生命周期三个阶…...
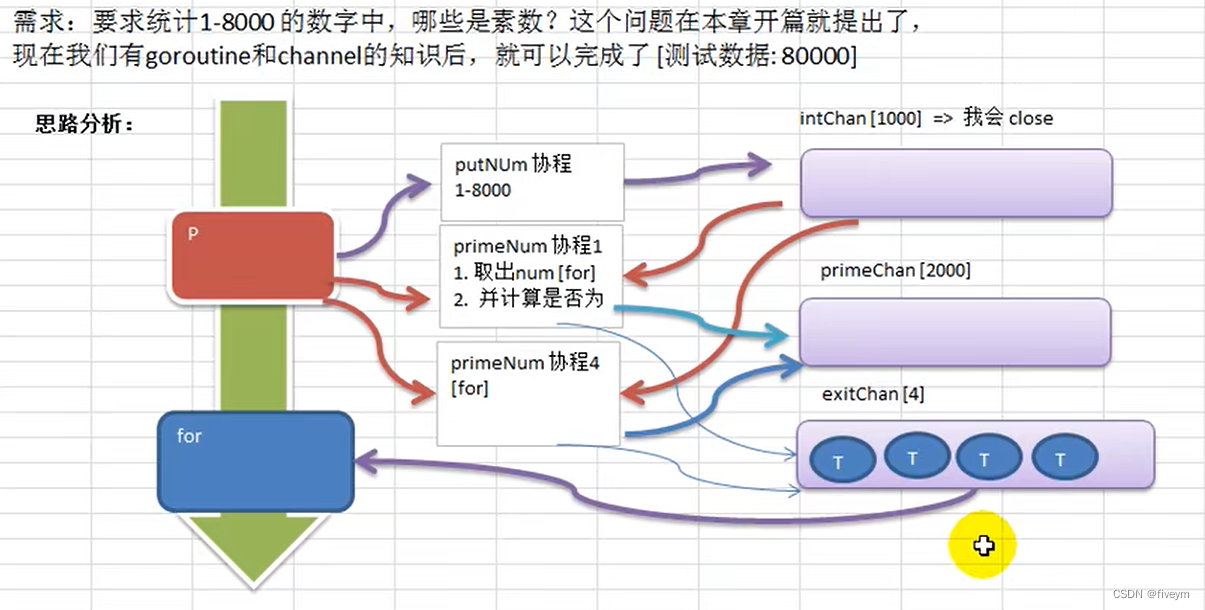
44-Golang中的channel
Golang中的channel为什么要使用channelchannel的介绍channel的基本使用定义/声明channel管道的遍历和关闭channel的关闭channel的遍历goroutine和channel结合应用实例1应用实例2案例注意事项为什么要使用channel 前面使用全局变量加锁同步来解决goroutine的通讯,但…...

80/20法则
80/20法则(The 80/20 Rule)又称为帕累托法则(Pareto Principle)、二八定律、帕累托定律、最省力法则、不平衡原则、犹太法则、马特莱法则等一、什么是80/20法则80/20法则(The 80/20 Rule),又称为帕累托法则…...
)
计算机网络高频面试题(四)
一、什么是计算机网络 是一个将分散的、具有独立功能的计算机系统,通过通信设备与线路连接起来,由功能完善的软件实现资源共享和信息传递的系统 按分布范围,计算机网络里有局域网LAN和广域网WAN, 其中局域网的代表以太网,以及这…...
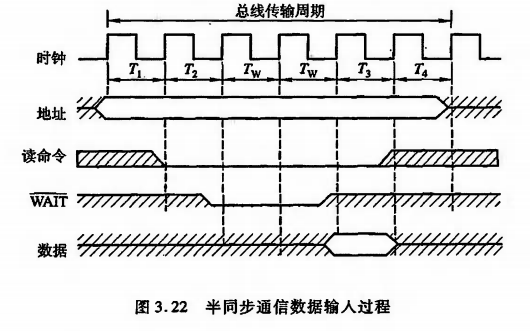
[计算机组成原理(唐朔飞 第2版)]第三章 系统总线(学习复习笔记)
3.1 总线的基本概念 计算机系统的五大部件之间的互连方式有两种 各部件之间使用单独的连线,称为分散连接将各部件连到一组公共信息传输线上,称为总线连接 总线是连接多个部件的信息传输线,是各部件共享的传输介质。 当多个部件与总线相连时&…...
| 机考必刷)
华为OD机试题 - 计算堆栈中的剩余数字(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:计算堆栈中的剩余数字题目输入输出描述示例一输入输出说明示例二…...

VB实现点爆炸效果
需在窗体放置以下 4 个控件,所有控件不用设置任何属性,均采用默认设置: ’ Picture1,Command1,Check1,Timer1 Option Explicit Dim I Dim ctD() As tyD, ctDs As Long, ctR As Single Private Type tyD x…...
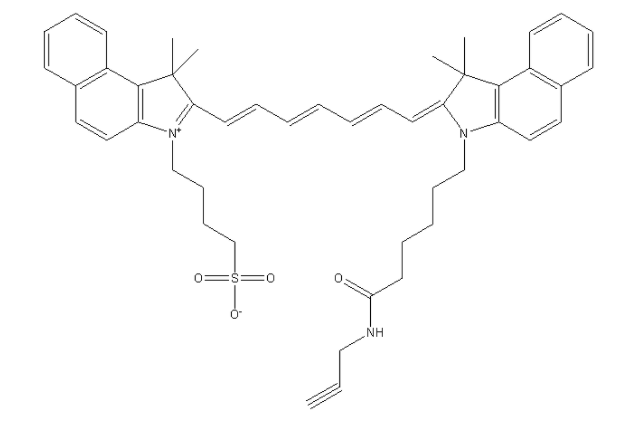
ICG-alkyne,吲哚菁绿-炔基结构式,实验室科研试剂,CAS号:1622335-41-4
ICG-alkyne,吲哚菁绿-炔基 中文名称:吲哚菁绿-炔基 CAS号:1622335-41-4 英文名称:ICG-alkyne 英文别名:ICG-alk 性状:绿色粉末 化学式:C48H53N3O4S 分子量:768.03 溶剂:溶于…...

【并发编程】volatile的原理我好像又懂了
文章目录优秀引用1、概述2、可见性保证2.1、什么是可见性2.2、例子举证2.3、结果解析3、有序性保证3.1、什么是有序性3.2、什么是重排序3.3、例子举证4、无法保证原子性4.1、什么是原子性4.2、例子举证5、内存屏障5.1、什么是内存屏障5.2、不同内存屏障的作用6、volatile和sync…...

【已更新实例】Java网络爬虫-HttpClient工具类
关于用Java进行爬虫的资料网上实在少之又少,但作为以一名对Java刚刚初窥门径建立好兴趣的学生怎么能静得下心用新学的Python去写,毕竟Java是世界上最好的语言嘛 (狗头)关于Java爬虫最受欢迎的一个框架Jsoup常常搭配HttpClient来使用,因为Jsou…...

7.2 向量的坐标
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

SQL Server 触发器调用存储过程实现发送 HTTP 请求
文章目录 需求分析解决第 1 步:前置条件,启用 OLE 自动化方式 1:使用 SQL 实现启用 OLE 自动化方式 2:Sql Server 2005启动OLE自动化方式 3:Sql Server 2008启动OLE自动化第 2 步:创建存储过程第 3 步:创建触发器扩展 - 如何调试?第 1 步:登录 SQL Server 2008第 2 步…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...
