关于椭圆的方程(有Python画的动图)
关于椭圆的方程(有Python画的动图)
flyfish

几何定义
椭圆是平面上所有到两个固定点(焦点)的距离之和为常数的点的集合。这两个固定点叫做焦点。
解析几何描述
设椭圆的两个焦点为 F 1 F_1 F1 和 F 2 F_2 F2,焦距(两焦点之间的距离的一半)为 c c c,长轴的半长轴为 a a a,短轴的半短轴为 b b b,椭圆上任意一点到这两个焦点的距离之和是一个常数 2 a 2a 2a。如果椭圆的中心在原点,长轴平行于 x x x 轴,则椭圆的标准方程为: x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1如果长轴平行于 y y y 轴,只需交换 a a a 和 b b b 的位置: x 2 b 2 + y 2 a 2 = 1 \frac{x^2}{b^2} + \frac{y^2}{a^2} = 1 b2x2+a2y2=1
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.animation import FuncAnimation, PillowWriterdef plot_ellipse_with_moving_point(a, b, num_frames=100, interval=50):# 椭圆方程参数theta = np.linspace(0, 2 * np.pi, num_frames)x = a * np.cos(theta)y = b * np.sin(theta)# 焦点位置c = np.sqrt(a**2 - b**2)F1 = (-c, 0)F2 = (c, 0)# 创建图形fig, ax = plt.subplots(figsize=(8, 6))ax.plot(x, y, label=f'Ellipse: $\\frac{{x^2}}{{{a}^2}} + \\frac{{y^2}}{{{b}^2}} = 1$')ax.scatter(*F1, color='red')ax.scatter(*F2, color='red')ax.text(F1[0], F1[1], 'F1', fontsize=12, ha='right')ax.text(F2[0], F2[1], 'F2', fontsize=12, ha='left')ax.axhline(0, color='black', linewidth=0.5)ax.axvline(0, color='black', linewidth=0.5)ax.grid(color='gray', linestyle='--', linewidth=0.5)ax.set_aspect('equal', adjustable='box')ax.set_title('Ellipse with Moving Point')ax.set_xlabel('x')ax.set_ylabel('y')ax.legend()# 初始化点 P 和连接线point, = ax.plot([], [], 'bo')line1, = ax.plot([], [], 'gray', linestyle='dotted')line2, = ax.plot([], [], 'gray', linestyle='dotted')# 初始化函数def init():point.set_data([], [])line1.set_data([], [])line2.set_data([], [])return point, line1, line2# 更新函数def update(frame):P = (a * np.cos(theta[frame]), b * np.sin(theta[frame]))point.set_data([P[0]], [P[1]])line1.set_data([F1[0], P[0]], [F1[1], P[1]])line2.set_data([F2[0], P[0]], [F2[1], P[1]])return point, line1, line2# 创建动画ani = FuncAnimation(fig, update, frames=num_frames, init_func=init, interval=interval, blit=True)# 保存动画ani.save('ellipse_with_moving_point.gif', writer=PillowWriter(fps=20))plt.show()# 参数
a = 5
b = 3
plot_ellipse_with_moving_point(a, b)
相关文章:

关于椭圆的方程(有Python画的动图)
关于椭圆的方程(有Python画的动图) flyfish 几何定义 椭圆是平面上所有到两个固定点(焦点)的距离之和为常数的点的集合。这两个固定点叫做焦点。 解析几何描述 设椭圆的两个焦点为 F 1 F_1 F1 和 F 2 F_2 F2ÿ…...
selenium常见难点解决方案
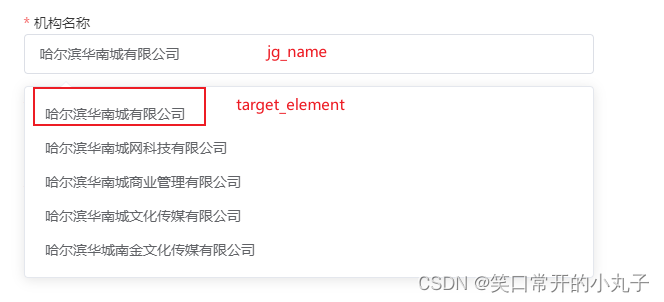
勾选框勾选问题 勾选框代码逻辑实现过程: 第一步:首先找到勾选框的元素; 第二步:检查它是否已经被勾选。如果已经勾选,则进行取消勾选操作;如果未勾选,则进行点击勾选操作; 以下是一…...

【Python高级编程】 综合练习-使用OpenCV 进行视频数据处理
综合练习 读取一个视频文件,对其进行处理后保存为一个新的视频文件。具体的处理步骤包括调整帧大小、转换为灰度图像、垂直翻转画面以及添加高斯噪声。 下面是代码的详细实现: import cv2 import numpy as np# 定义一个函数,用来给图像添加…...

rs232和can的区别
在电机通讯和升级固件时我们经常用到RS232和CAN两种通讯模式,那这两种有何不同吗? RS232和CAN的主要区别在于通信方式、应用场景、传输距离、通信速度以及网络结构。 通信方式: RS232是一种串行通信接口标准,支持全双工通信&…...

嵌入式软件stm32面试
一、STM32的内核型号有哪些? STM32系列是STMicroelectronics(意法半导体)生产的基于ARM Cortex-M内核的微控制器产品线。这些产品按照不同的内核架构和性能特点分为了主流产品、超低功耗产品和高性能产品。 1.1 主流产品 STM32F0 系列&…...
【Git】-- 添加公钥到 github 或者gitlab上
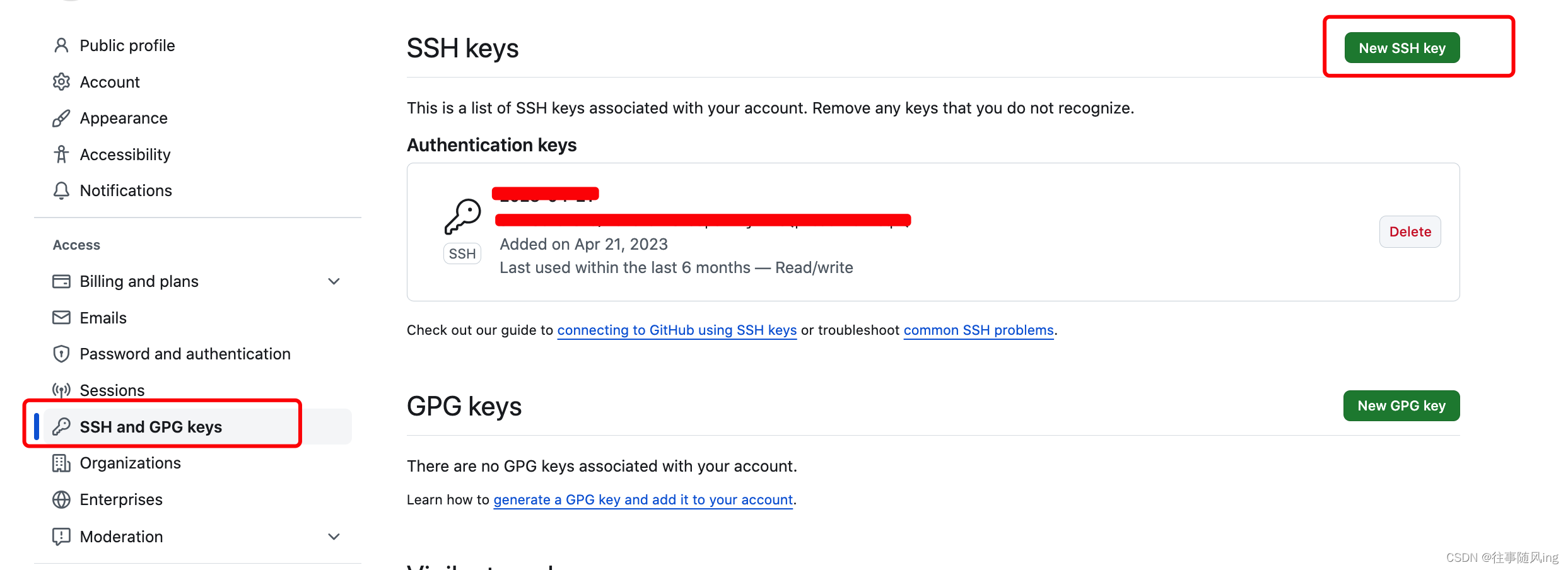
仅针对系统:mac os 、 unix、linux 1、检查是否有 id_rsa.pub $ cd ~ $ ls -al ~/.ssh 注意:若已有 id_rsa.pub,则必要执行 第二步,避免覆盖掉原有正常的公钥。 配置多个 git 账号请参考:同一台电脑配置多个git账…...

Vue页面生成PDF后调起浏览器打印
一、安装依赖 首先,需要安装 html2canvas 和 jsPDF 库。 npm install html2canvas jspdf二、创建公共方法引入 在utils文件夹下创建两个文件分别为pdfExport.js和printPDF.js,代码如下: pdfExport.js import html2canvas from html2canv…...

纯前端实现导出excel
项目背景: vue2 插件: xlsx;xlsx-style;file-saver 说明: 单独使用 xlsx插件,也可以将网页上的table导出成excel,但是导出的excel,没有样式 结合xlsx-style;file-saver&a…...

QT windows 5.12.0 安装包
这个是在线包,需要有账号的。 没有也没事,安装界面可以现场注册 百度网盘链接: 链接:https://pan.baidu.com/s/1QvXDert4b94GbUfD2f2G4g?pwd8888 提取码:8888...

改进YOLOv7 | 在 ELAN 模块中添加【Triplet】【SpatialGroupEnhance】【NAM】【S2】注意力机制 | 附详细结构图
改进 YOLOv7 | 在 ELAN 模块中添加【Triplet】【SpatialGroupEnhance】【NAM】【S2】注意力机制:中文详解 1. 简介 YOLOv7 是目前主流的目标检测算法之一,具有速度快、精度高的特点。但 YOLOv7 的原始模型结构中缺乏注意力机制,导致模型对全…...

windows系统停止更新办法
windows系统停止更新 双击启动下载的文件 然后再回到系统-更新这里,选择日期就行。...

数据标注概念
数据标注的步骤 数据清洗:处理数据中的噪声、缺失值和异常值,确保数据的质量和完整性。 数据转换:将数据从原始格式转换为适合机器学习模型处理的格式。 数据标注:根据应用需求,为数据添加标签或注释,标识…...

网络安全复习笔记
概述 要素 CIA:可用性;完整性;保密性。 可控性;不可否认性;可审查性。 攻击 被动:窃听 - 保密性;监听 - 保密性主动:假冒 - 完整性;重放 - 完整性;改写 -…...
Laravel - excel 导入数据
在Laravel中,可以使用maatwebsite/excel这个库来处理Excel文件的导入。 1.用命令行窗口打开项目根目录,使用 Composer 安装 maatwebsite/excel composer require maatwebsite/excel --ignore-platform-reqs 在你的config/app.php文件中注册服务提供者&…...

移动语义和完美转发
C11 引入了许多新特性,使得编写高效且现代的 C 代码变得更加容易。其中,移动语义(Move Semantics)和完美转发(Perfect Forwarding)是两个重要的特性,极大地提升了 C 的性能和灵活性。 移动语义…...
【IDEA】Spring项目build失败
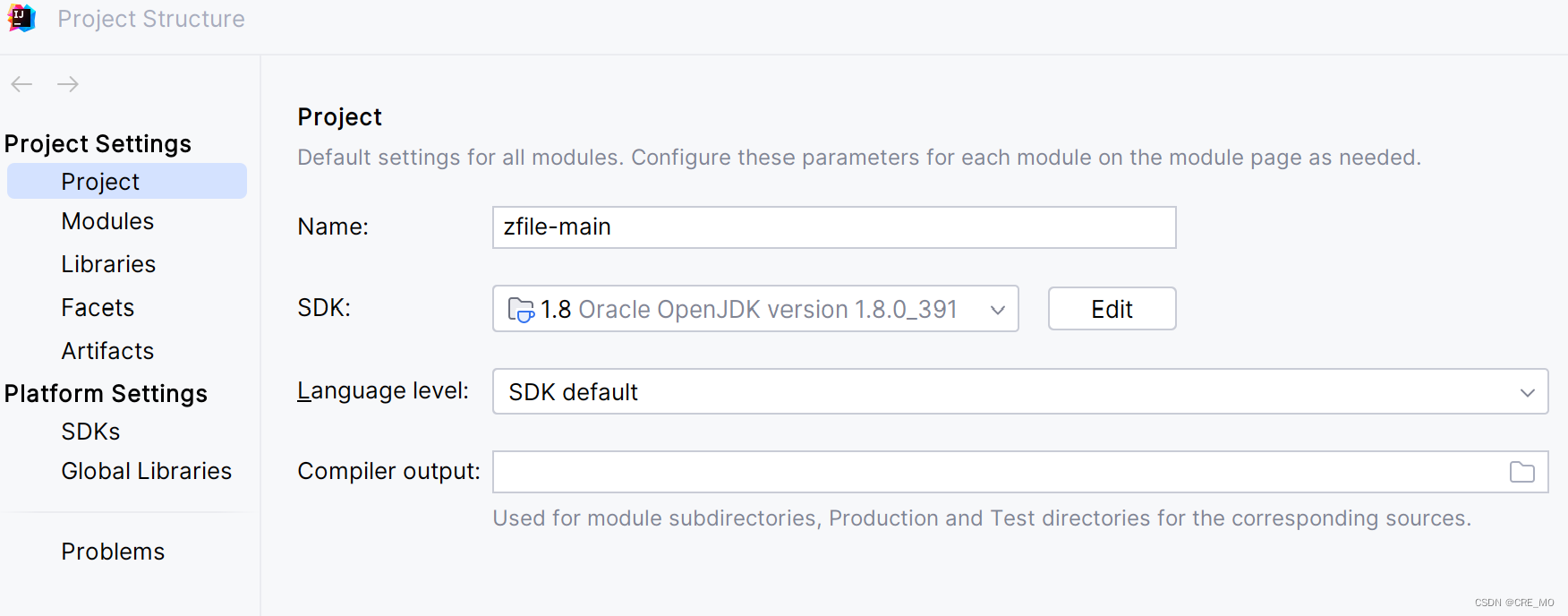
通常因为环境不匹配需要在file->projectstructure里面调整一下。...

【无标题】安卓app 流量
该工具可以用于安卓app 流量,内存,cpu,fps等专项内容测试,并且有整机内存,cpu对比,还可监控手机网速,app流量,数据导出等功能,重点还是免费,毕竟PerfDog收费了…...
国产化ETL产品必备的特性(非开源包装)
ETL负责将分布的、异构数据源中的数据如关系数据、平面数据文件等抽取到临时中间层后进行抽取、清洗(净化)、转换、装载、标准、集成(汇总)...... 最后加载到数据仓库或数据集市中,成为联机分析处理、数据挖掘的基础。…...

flink 操作mongodb的例子
Apache Flink 是一个流处理和批处理的开源框架,它通常用于处理大量数据流。然而,Flink 本身并不直接提供对 MongoDB 的原生支持,因为 MongoDB 是一个 NoSQL 数据库,而 Flink 主要与关系型数据库(如 JDBC 连接器&#x…...

【笔记】打卡01 | 初学入门
初学入门:01-02 01 基本介绍02 快速入门库处理数据集网络构建模型训练保存模型加载模型打卡-时间 01 基本介绍 MindSpore Data(数据处理层) ModelZoo(模型库) MindSpore Science(科学计算),包含…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

mac 安装homebrew (nvm 及git)
mac 安装nvm 及git 万恶之源 mac 安装这些东西离不开Xcode。及homebrew 一、先说安装git步骤 通用: 方法一:使用 Homebrew 安装 Git(推荐) 步骤如下:打开终端(Terminal.app) 1.安装 Homebrew…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
