工具函数-算法
1. 实现四舍五入,保留两位小数
const v = 0.0635455;
// 方式1,保留2位小数,返回的是number格式
const formatted = Math.round(v * 100) / 100;
// 方式2,保留2位小数,返回的是字符串格式
const formatted = v.toFixed(2);
在使用浮点数运算时,有时会出现无限循环的情况,这是由于浮点数在转换成二进制的时候就会出现。将浮点数转换为二进制形式的过程如下:
-
将整数部分转换为二进制:
- 将整数部分除以 2,记录余数,直到商变为 0。余数倒序排列即为整数部分的二进制形式。
-
将小数部分转换为二进制:
- 将小数部分乘以 2,取整数部分作为二进制位,小数部分继续乘以 2,直到小数部分为 0 或达到所需的精度。
举例:一个典型的例子就是 0.1 这个值,将 0.1 转换为二进制的过程如下:
- 小数部分 0.1 乘以 2:
- 0.1 × 2 = 0.2 (取整数部分 0)
- 小数部分 0.2 乘以 2:
- 0.2 × 2 = 0.4 (取整数部分 0)
- 小数部分 0.4 乘以 2:
- 0.4 × 2 = 0.8 (取整数部分 0)
- 小数部分 0.8 乘以 2:
- 0.8 × 2 = 1.6 (取整数部分 1)
重复这个过程,我们会发现小数部分会产生一个无限循环的二进制序列。
因此尽量不要直接将对浮点数的运算结果直接展示出来。
2. 随机数算法
生成一个固定范围的随机数:min + (max-min)*Math.random()
生成一个随机排列 [1, 2, 3, 4].sort((a, b) => return Math.random() - 0.5)
快速取整:<< 0和 >> 0都是取整,是js里性能最快的取整,不管正负数都是去掉小数部分;和Math.floor、Math.ceil、Math.round不一样。
例如: 1.23 >> 0 -> 1 -2.59 << 0 -> -2
3. 轮播图取值
取值逻辑 fix: i => ((i % length) + length) % length
这个函数的作用是修正给定的索引 i,使其始终处于 0 到 length-1 的范围内。这对于轮播组件非常有用,因为当用户点击上一个或下一个按钮时,索引可能会超出 0 到 length-1 的范围。
这个函数的实现原理如下:
-
i % length: 这个操作可以将i限制在0到length-1的范围内。但是,如果i为负数,这个操作会返回一个负数。 -
(i % length) + length: 这个操作可以确保结果始终为非负数。如果i为负数,i % length会返回一个负数,但加上length后会变成一个正数。 -
((i % length) + length) % length: 这个最后的取模操作可以确保结果在0到length-1的范围内。即使(i % length) + length的结果大于length,取模操作也会将其缩减到0到length-1的范围内。
总之,这个 fix 函数可以确保无论 i 的值是多少,它都会被修正为 0 到 length-1 之间的一个合法索引。这对于轮播组件的实现非常重要,可以确保组件的行为是可预测的,无论用户的操作如何。
相关文章:

工具函数-算法
1. 实现四舍五入,保留两位小数 const v 0.0635455; // 方式1,保留2位小数,返回的是number格式 const formatted Math.round(v * 100) / 100; // 方式2,保留2位小数,返回的是字符串格式 const formatted v.toFixed(…...
C# yolov8 OpenVINO 同步、异步接口视频推理
C# yolov8 OpenVINO 同步、异步接口视频推理 目录 效果 项目 代码 下载 效果 同步推理效果 异步推理效果 项目 代码 using OpenCvSharp; using System; using System.Collections.Generic; using System.Diagnostics; using System.Threading; using System.Windows.Form…...
【STM32入门学习】定时器与PWM的LED控制
目录 一、定时器与PWM介绍 1.1定时器 1.1.1定时器分类简介 1.1.2STM32定时器分类比较表 1.1.3定时器启动操作: 1.2 PWM 1.2.1 简介: 1.2.2PWM工作原理 1.2.3使用步骤: 二、定时器计数控制LED灯亮灭 2.1HAL库 2.1.1使用HAL库创建…...
PyTorch实战:模型训练中的特征图可视化技巧
1.特征图可视化,这种方法是最简单,输入一张照片,然后把网络中间某层的输出的特征图按通道作为图片进行可视化展示即可。 2.特征图可视化代码如下: def featuremap_visual(feature, out_dirNone, # 特征图保存路径文件save_feat…...

有人@你!神工坊知识问答第二期中奖名单新鲜出炉
六月作为伟大的物理学家—麦克斯韦的诞辰月 神工坊特别推出 “ 辨 ‘麦克斯韦妖’,赢百元好礼” 夏日知识问答主题活动 活动一经推出 反响热烈 第二期中奖名单公布! 中奖的伙伴们速来兑奖! 听说还有同学没有参与? 活动最后…...

数据结构篇:旋转操作在AVL树中的实现过程
本节课在线学习视频(网盘地址,保存后即可免费观看): https://pan.quark.cn/s/06d5ed47e33b AVL树是平衡二叉搜索树的一种,它通过旋转操作来保持树的平衡。AVL树的特点是,任何节点的两个子树的高度最大差别…...

为什么Java默认使用UTF-16,Golang默认使用UTF-8呢?
Java 和 Go 语言在默认字符编码上做出了不同的选择,这是由它们的设计目标和使用场景决定的。下面是对 Java 默认使用 UTF-16 和 Go 默认使用 UTF-8 的原因进行的详细解释。 Java 默认使用 UTF-16 的原因 1. 历史背景和兼容性 Unicode 的发展: Java 诞生于 1995 年…...
)
JavaScript常见面试题(三)
文章目录 1.对原型、原型链的理解2.原型修改、重写3.原型链指向4.对闭包的理解5. 对作用域、作用域链的理解6.对执行上下文的理解7.对this对象的理解8. call() 和 apply() 的区别?9.异步编程的实现方式?10.setTimeout、Promise、Async/Await 的区别11.对…...

【Effective Modern C++】第1章 型别推导
【Effective Modern C】第1章 型别推导 文章目录 【Effective Modern C】第1章 型别推导条款1:理解模板型别推导基础概念模板型别推导的三种情况情景一 ParamType 是一个指针或者引用,但非通用引用情景二 ParamType是一个通过引用情景三 ParamType既不是…...
服装连锁实体店bC一体化运营方案
一、引言 随着互联网的快速发展和消费者购物习惯的变化,传统服装连锁实体店在面对新的市场环境下亟需转型升级。BC(Business to Consumer)一体化运营方案的实施将成为提升服装连锁实体店竞争力和顾客体验的关键举掖。商淘云详细介绍服装连锁…...
IDEA中SpringMVC的运行环境问题
文章目录 一、IEAD 清理缓存二、用阿里云和spring创建 SpringMVC 项目中 pom.xml 文件的区别 一、IEAD 清理缓存 springMVC 运行时存在一些之前运行过的缓存导致项目不能运行,可以试试清理缓存 二、用阿里云和spring创建 SpringMVC 项目中 pom.xml 文件的区别 以下…...

Python初体验
# Java基础知识学的差不多了,项目上又没什么事,学学py,方便以后对接 1、打包flask应用(好痛苦,在什么平台打包就只在那个平台可用想在linux用只能参考方法2了) pyinstaller --onefile app.py -n myapp 2…...

从零开始如何学习人工智能?
说说我自己的情况:我接触AI的时候,是在研一。那个时候AlphaGo战胜围棋世界冠军李世石是大新闻,人工智能第一次出现我面前,当时就想搞清楚背后的原理以及这些技术有什么作用。 就开始找资料,看视频。随着了解的深入&am…...

【仿真建模-anylogic】动态生成ConveyorCustomStation
Author:赵志乾 Date:2024-06-18 Declaration:All Right Reserved!!! 0. 背景 直接使用Anylogic组件开发的模型无法动态改变运输网布局;目前需求是要将运输网布局配置化;运输网配置化…...
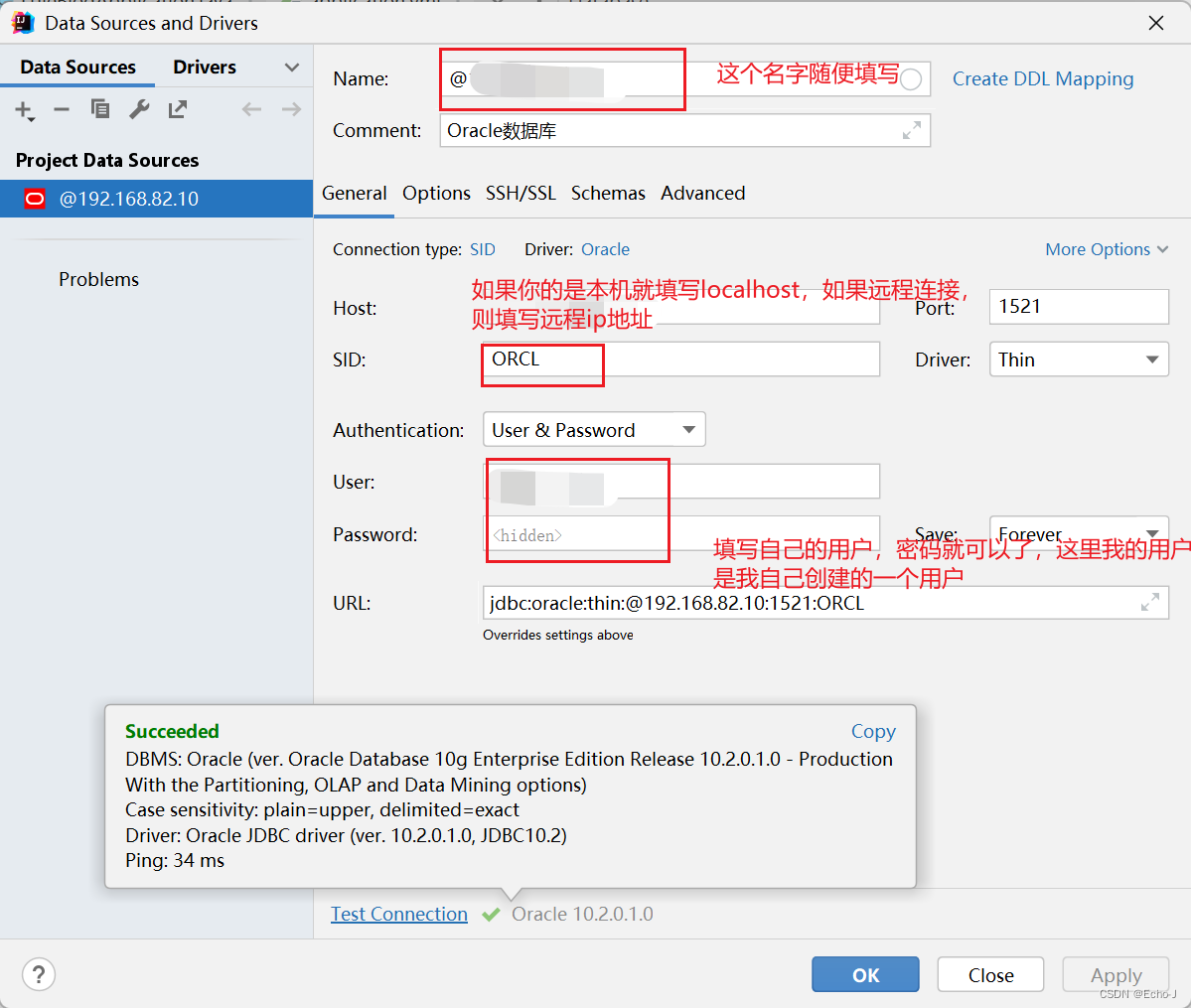
如何使用idea连接Oracle数据库?
idea版本:2021.3.3 Oracle版本:10.2.0.1.0(在虚拟机Windows sever 2003 远程连接数据库) 数据库管理系统:PLSQL Developer 在idea里面找到database,在idea侧面 选择左上角加号,新建ÿ…...

谈谈kafaka的并行处理,顺带讲讲rabbitmq
简介 Kafka 是一个分布式流处理平台,它支持高效的并行处理。Kafka 的并行处理能力主要体现在以下几个方面: 分区(Partition)并行 Kafka 将数据存储在称为"分区"的逻辑单元中。每个分区可以独立地并行地进行读写操作。生产者可以根据分区策略,将数据写入到指定的分…...

P3056 [USACO12NOV] Clumsy Cows S
[USACO12NOV] Clumsy Cows S 题目描述 Bessie the cow is trying to type a balanced string of parentheses into her new laptop, but she is sufficiently clumsy (due to her large hooves) that she keeps mis-typing characters. Please help her by computing the min…...

智赢选品,OZON数据分析选品利器丨萌啦OZON数据
在电商行业的激烈竞争中,如何快速准确地把握市场动态、洞察消费者需求、实现精准选品,是每个电商卖家都面临的挑战。而在这个数据驱动的时代,一款强大的数据分析工具无疑是电商卖家们的得力助手。今天,我们就来聊聊这样一款选品利…...

Canal自定义客户端
一、背景 在Canal推送数据变更信息至MQ(消息队列)时,我们遇到了特定问题,尤其是当消息体的大小超过了MQ所允许的最大限制。这种限制导致数据推送过程受阻,需要相应的调整或处理。 二、解决方法 采用Canal自定义客户…...
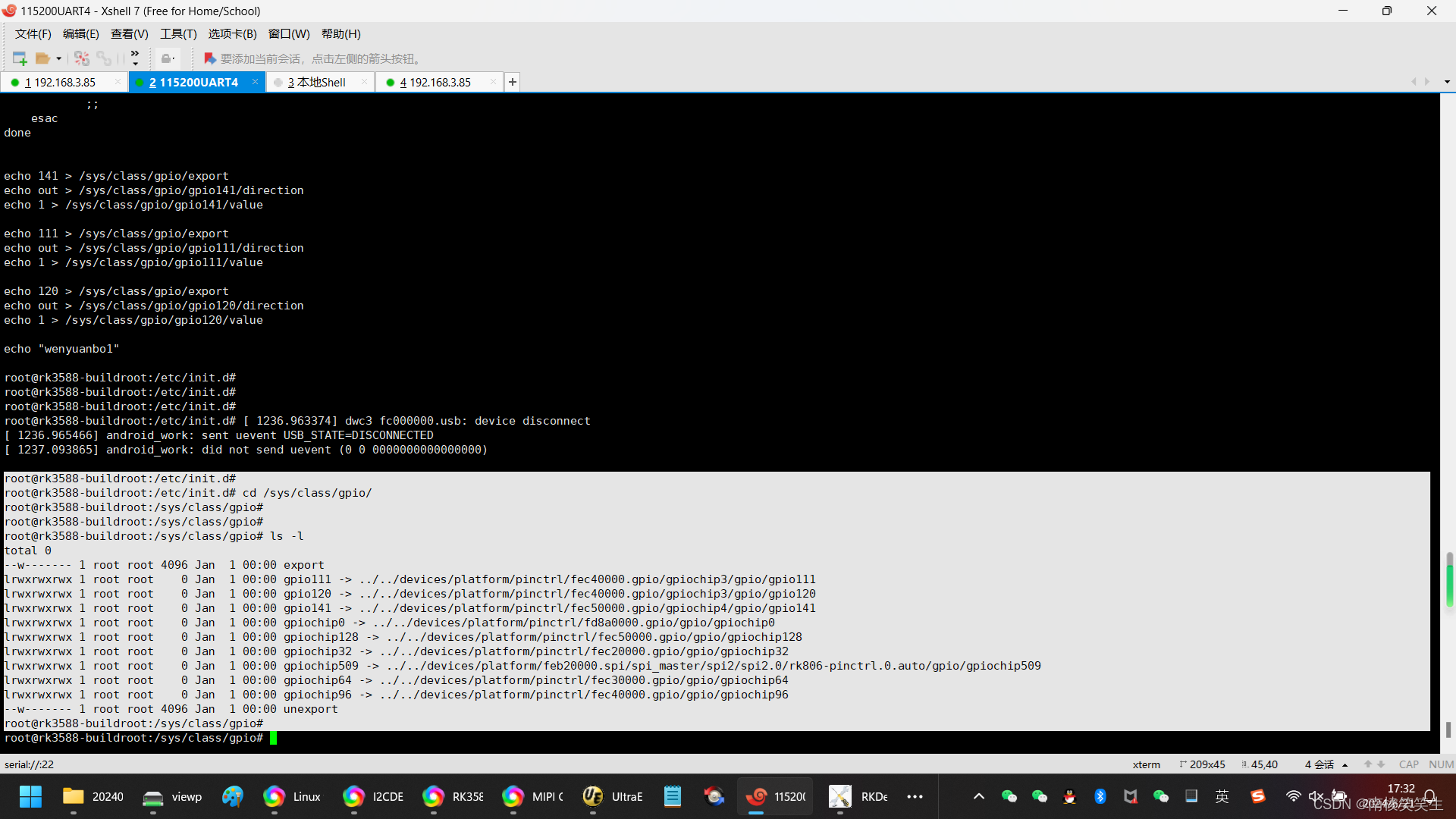
20240621将需要自启动的部分放到RK3588平台的Buildroot系统的rcS文件中
20240621将需要自启动的部分放到RK3588平台的Buildroot系统的rcS文件中 2024/6/21 17:15 开发板:飞凌OK3588-C SDK:Rockchip原厂的Buildroot 缘起:在凌OK3588-C的LINUX R4系统启动的时候,需要拉高GPIO4_B5、GPIO3_B7和GPIO3_D0。…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
