[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
- 一、题目
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 提示
- 数据规模与约定
- 二、分析
- 1、递归建树
- 2、树形DP + 状态机DP
- (1)状态表示
- (2)状态转移
- 三、代码
一、题目
题目描述
一棵二叉树可以按照如下规则表示成一个由 000、111、222 组成的字符序列,我们称之为“二叉树序列 SSS”:
S={0表示该树没有子节点1S1表示该树有一个节点,S1为其子树的二叉树序列2S1S2表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列S= \begin{cases} 0& \text表示该树没有子节点\\ 1S_1& 表示该树有一个节点,S_1 为其子树的二叉树序列\\ 2S_1S_2& 表示该树由两个子节点,S_1 和 S_2 分别表示其两个子树的二叉树序列 \end{cases}S=⎩⎨⎧01S12S1S2表示该树没有子节点表示该树有一个节点,S1为其子树的二叉树序列表示该树由两个子节点,S1和S2分别表示其两个子树的二叉树序列
例如,下图所表示的二叉树可以用二叉树序列 S=21200110S=\texttt{21200110}S=21200110 来表示。
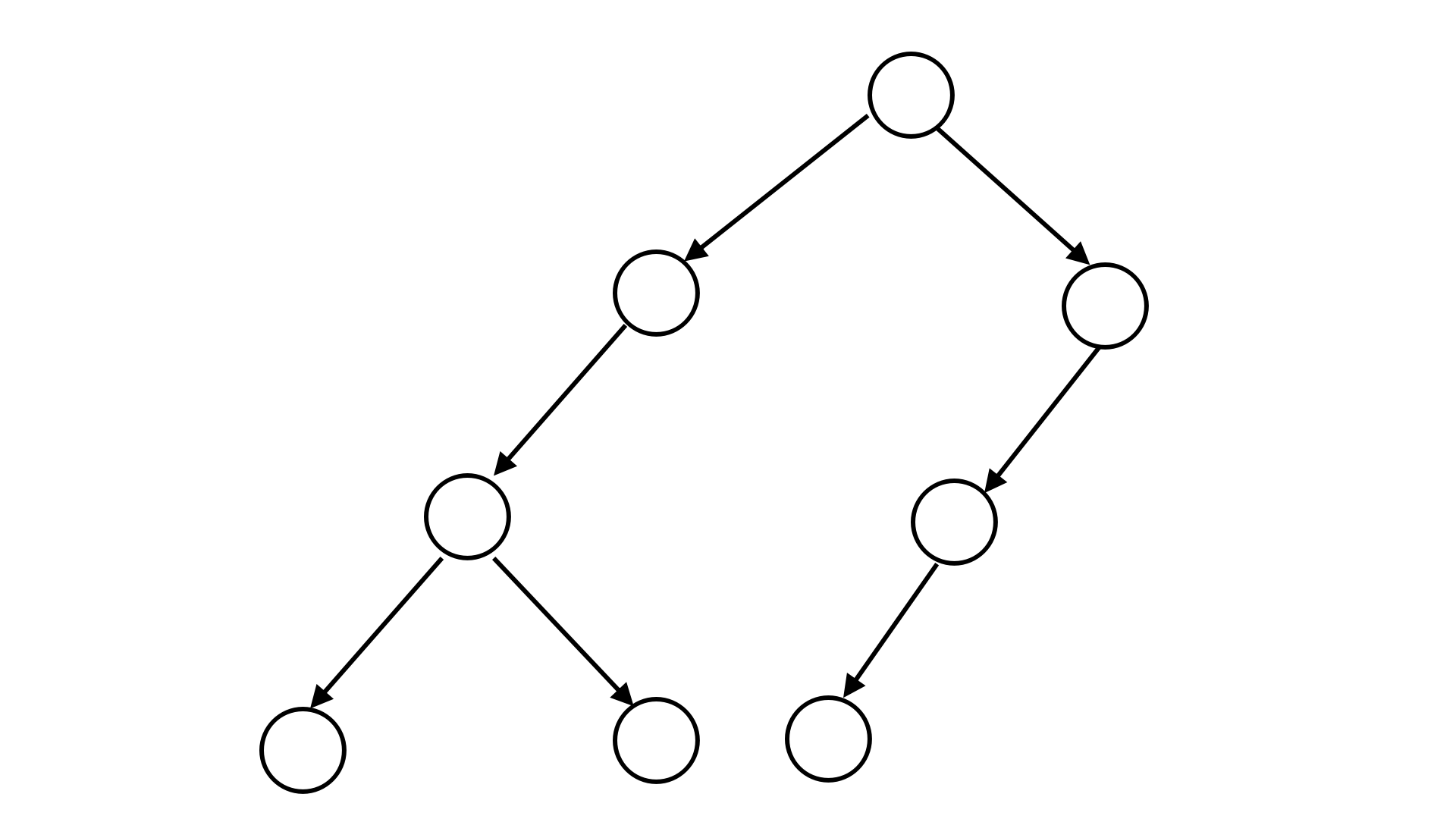
你的任务是要对一棵二叉树的节点进行染色。每个节点可以被染成红色、绿色或蓝色。并且,一个节点与其子节点的颜色必须不同,如果该节点有两个子节点,那么这两个子节点的颜色也必须不同。给定一颗二叉树的二叉树序列,请求出这棵树中最多和最少有多少个点能够被染成绿色。
输入格式
输入只有一行一个字符串 sss,表示二叉树序列。
输出格式
输出只有一行,包含两个数,依次表示最多和最少有多少个点能够被染成绿色。
样例 #1
样例输入 #1
1122002010
样例输出 #1
5 2
提示
数据规模与约定
对于全部的测试点,保证 1≤∣s∣≤5×1051 \leq |s| \leq 5 \times 10^51≤∣s∣≤5×105,sss 中只含字符 0 1 2。
二、分析
这道题有两个难点:
第一个难点是如何递归建树。
第二个难点则是我们如何写DP转移方程。
1、递归建树
题目中给了我们一个字符串,这个字符串的长度就是树中所有节点的个数。那么我们就先从左到右给这些点进行一个编号。
这个编号的过程我们用一个全局变量tottottot表示。
因为这是一个二叉树,所以它总共就分为三种情况,没有子树,一个子树,两个子树。
我们定义一个DFS函数:这个DFS的作用是建立以uuu为根节点的树。
如果当前字符串中对应的字符是000,则说明当前的点是叶子节点,我们将叶子节点插入到树中后,就无需向下递归(因为叶子节点没有子树),直接返回即可。
如果当前字符串中对应的字符是111,则说明当前节点有一个子树,所以我们就需要去继续DFS。
如果当前字符串中对应的字符是222,说明当前节点有两个子树,则我们需要先去递归第一个子树,当第一个子树建成以后,再去建第二个子树。
//递归建树
void dfs(int root)
{tot ++;if(str[root] == '0')return;if(str[root] == '1'){edge[root + 1].push_back(root + 2);dfs(root + 1);}if(str[root] == '2'){edge[root + 1].push_back(root + 2);dfs(root + 1);edge[root + 1].push_back(tot + 1);dfs(tot);}
}
2、树形DP + 状态机DP
我们以最大值为例,最小值就是将取最大值的过程改成取最小值。
因为子树的颜色状态影响到了当前点的染色选择,所以我们需要对所有的染色情况进行讨论,同时用0,1,2三个数字表示当前的染色情况。
(1)状态表示
f[u][0]f[u][0]f[u][0] : 以u为根节点,u为绿色, 最多的绿色点个数。
f[u][1]f[u][1]f[u][1]: 以u为根节点, u为红色, 最多的绿色点个数。
f[u][2]f[u][2]f[u][2]: 以u为根节点, u为蓝色, 最多的绿色点个数。
(2)状态转移
如果当前节点是叶子节点,那么只需要给当前节点染色,状态方程为:
f[u][0]=1f[u][1]=0f[u][2]=0f[u][0]=1\\ f[u][1]=0\\ f[u][2]=0 f[u][0]=1f[u][1]=0f[u][2]=0
如果当前节点只有一个子树,那么状态转移方程为:
f[u][0]=max(f[son][1],f[son][2])+1f[u][1]=max(f[son][0],f[son][2])f[u][2]=max(f[son][1],f[son][0])f[u][0]=max(f[son][1],f[son][2])+1 \\f[u][1]=max(f[son][0],f[son][2]) \\f[u][2]=max(f[son][1],f[son][0]) f[u][0]=max(f[son][1],f[son][2])+1f[u][1]=max(f[son][0],f[son][2])f[u][2]=max(f[son][1],f[son][0])
如果当前节点有两个子树的话,那么状态转移方程为:
f[u][0]=max(f[son1][1]+f[son][2],f[son1][2]+f[son2][1])+1f[u][1]=max(f[son1][0]+f[son2][2],f[son1][2]+f[son2][0])f[u][2]=max(f[son1][0]+f[son2][1],f[son1][1]+f[son2][0])f[u][0]=max(f[son1][1]+f[son][2],f[son1][2]+f[son2][1])+1 \\f[u][1]=max(f[son1][0]+f[son2][2],f[son1][2]+f[son2][0]) \\f[u][2]=max(f[son1][0]+f[son2][1],f[son1][1]+f[son2][0]) f[u][0]=max(f[son1][1]+f[son][2],f[son1][2]+f[son2][1])+1f[u][1]=max(f[son1][0]+f[son2][2],f[son1][2]+f[son2][0])f[u][2]=max(f[son1][0]+f[son2][1],f[son1][1]+f[son2][0])
三、代码
#include<bits/stdc++.h>
#define endl '\n'
#define INF 0x3f3f3f3f
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
const int N = 5e5 + 10;
string str;
int f[N][3];
int g[N][3];
int tot = 0;
vector<int>edge[N];//递归建树
void dfs(int root)
{tot ++;if(str[root] == '0')return;if(str[root] == '1'){edge[root + 1].push_back(root + 2);dfs(root + 1);}if(str[root] == '2'){edge[root + 1].push_back(root + 2);dfs(root + 1);edge[root + 1].push_back(tot + 1);dfs(tot);}
}void dp(int u)
{if(edge[u].size() == 1){int son = edge[u][0];dp(son);f[u][0] = max(f[son][1], f[son][2]) + 1;f[u][1] = max(f[son][2], f[son][0]);f[u][2] = max(f[son][0], f[son][1]);g[u][0] = min(g[son][1], g[son][2]) + 1;g[u][1] = min(g[son][2], g[son][0]);g[u][2] = min(g[son][0], g[son][1]);}else if(edge[u].size() == 2){int son1 = edge[u][0], son2 = edge[u][1];dp(son1);dp(son2);f[u][0] = max(f[son1][1] + f[son2][2], f[son1][2] + f[son2][1]) + 1;f[u][1] = max(f[son1][0] + f[son2][2], f[son1][2] + f[son2][0]);f[u][2] = max(f[son1][0] + f[son2][1], f[son1][1] + f[son2][0]);g[u][0] = min(g[son1][1] + g[son2][2], g[son1][2] + g[son2][1]) + 1;g[u][1] = min(g[son1][0] + g[son2][2], g[son1][2] + g[son2][0]);g[u][2] = min(g[son1][0] + g[son2][1], g[son1][1] + g[son2][0]);}else{f[u][0] = 1;g[u][1] = g[u][2] = 0;g[u][0] = 1;return;}
}
/*
f[u][0] : 以u为根节点, u为绿色, 最多的绿色点
f[u][1] : 以u为根节点, u为红色, 最多的绿色点
f[u][2] : 以u为根节点, u为蓝色, 最多的绿色点
f[u][0] = max(f[u][0], f[son1][1] + f[son2][2]);
f[u][1] = max(f[u][1], f[son1][0] + f[son2][2]);
f[u][2] = max(f[u][2], f[son1][0] + f[son2][1]);
*/
void solve()
{memset(g, INF, sizeof g);cin >> str;dfs(0);dp(1);// for(int i = 1; i <= str.size(); i ++)// {// cout << i << ": ";// for(int j = 0; j < edge[i].size(); j ++ )// {// cout << edge[i][j] << " ";// }// cout << endl;// }cout << max(max(f[1][0], f[1][1]), f[1][2]) << " ";cout << min(min(g[1][0], g[1][1]), g[1][2]) << endl; return;
}int main()
{ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);solve();
}
相关文章:

[洛谷-P2585][ZJOI2006]三色二叉树(树形DP+状态机DP)
[洛谷-P2585][ZJOI2006]三色二叉树(树形DP状态机DP)一、题目题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1提示数据规模与约定二、分析1、递归建树2、树形DP 状态机DP(1)状态表示(2)状态转移三、…...

BI技巧丨计算组
PowerBI有三大工具,分别是DAX Studio,Tabular Editor和Bravo。 DAX Studio通常我们会用来进行性能分析和DAX调优使用,Bravo一般用来批量格式化DAX,而Tabular Editor主要的功能就是计算组。 计算组这个名词,相信很多小伙…...
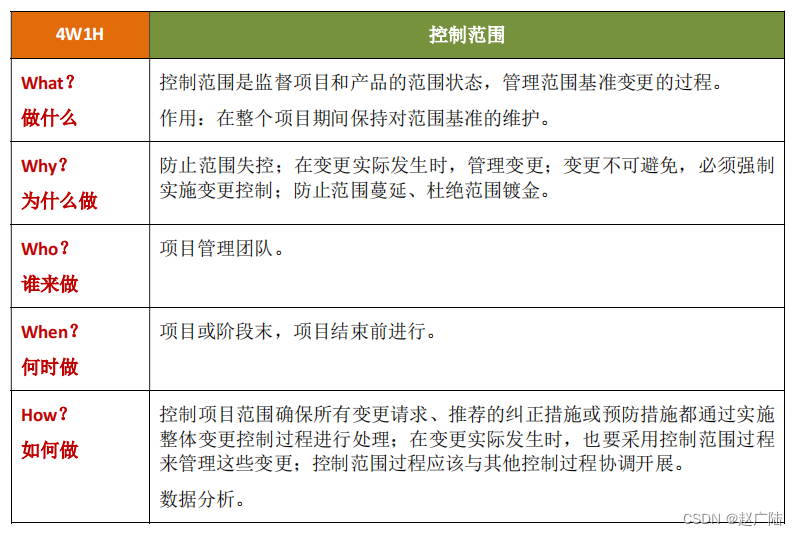
PMP项目管理项目范围管理
目录1 项目范围管理概述2 规划范围管理3 收集需求4 定义范围5 创建 WBS6 确认范围7 控制范围1 项目范围管理概述 项目范围管理包括确保项目做且只做所需的全部工作,以成功完成项目的各 个过程。管理项目范围主要在于定义和控制哪些工作应在项目内,哪些工…...

Flink 定时加载数据源
一、简介 flink 自定义实时数据源使用流处理比较简单,比如 Kafka、MQ 等,如果使用 MySQL、redis 批处理也比较简单 如果需要定时加载数据作为 flink 数据源使用流处理,比如定时从 mysql 或者 redis 获取一批数据,传入 flink 做处…...

ChatGPT、人工智能、人类和一些酒桌闲聊
© 2023 Conmajia Initiated 10th March, 2023 昨天跟某化学家喝酒,期间提到了 ChatGPT。他的评价是:这鬼东西大量输出毫无意义、错漏百出甚至是虚假的信息,“in a confident accent”。例如某次 GPT 针对“描述某某记者”这一问题&#…...

WebRTC开源库内部调用abort函数引发程序发生闪退问题的排查
目录 1、初始问题描述 2、使用Process Explorer工具查看到处理音视频业务的rtcmpdll.dll模块没有加载起来 3、使用Dependency Walker工具查看到rtcmpdll.dll依赖的库有问题 4、更新库之后Debug程序启动时就发生异常,程序闪退 5、VS调试时看不到有效的函数调用堆…...

Golang并发编程
Golang并发编程 文章目录Golang并发编程1. 协程2. channel2.1 channel的创建2.2 使用waitGroup实现同步3. 并发编程3.1 并发编程之runtime包3.2 mutex互斥锁3.3 channel遍历3.3.1 for if遍历3.3.2 for range3.4 select switch3.5 Timer3.5.1 time.NewTimer()3.5.2 Stop、reset…...
windows+Anaconda环境下安装BERT成功安装方法及问题汇总
前言 在WindowsAnaconda环境下安装BERT,遇到各种问题,几经磨难,最终成功。接下来,先介绍成功的安装方法,再附上遇到的问题汇总 成功的安装方法 1、创建虚拟环境 注意:必须加上python3.7.12以创建环境&a…...
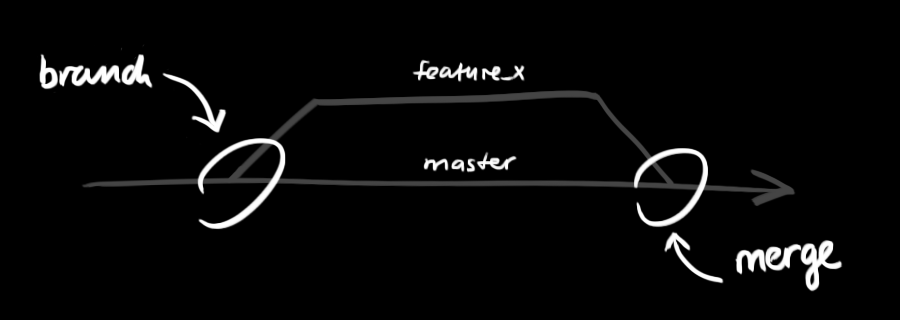
git - 简易指南
git - 简易指南 创建新仓库 创建新文件夹,打开,然后执行 git init 以创建新的 git 仓库。 检出仓库 执行如下命令以创建一个本地仓库的克隆版本: git clone /path/to/repository 如果是远端服务器上的仓库,你的命令会是这个样…...

[论文笔记]Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
引言 我们知道Transformer很好用,但它设定的最长长度是512。像一篇文章超过512个token是很容易的,那么我们在处理这种长文本的情况下也想利用Transformer的强大表达能力需要怎么做呢? 本文就带来一种处理长文本的Transformer变种——Transf…...
| 机考必刷)
华为OD机试题 - 找目标字符串(JavaScript)| 机考必刷
更多题库,搜索引擎搜 梦想橡皮擦华为OD 👑👑👑 更多华为OD题库,搜 梦想橡皮擦 华为OD 👑👑👑 更多华为机考题库,搜 梦想橡皮擦华为OD 👑👑👑 华为OD机试题 最近更新的博客使用说明本篇题解:找目标字符串题目输入输出示例一输入输出说明Code解题思路版权说…...

C++面向对象编程之六:重载操作符(<<,>>,+,+=,==,!=,=)
重载操作符C允许我们重新定义操作符(例如:,-,*,/)等,使其对于我们自定义的类类型对象,也能像内置数据类型(例如:int,float,double&…...

JS_wangEditor富文本编辑器
官网:https://www.wangeditor.com/ 引入 CSS 定义样式 <link href"https://unpkg.com/wangeditor/editorlatest/dist/css/style.css" rel"stylesheet"> <style>#editor—wrapper {border: 1px solid #ccc;z-index: 100; /* 按需定…...

Django实践-06导出excel/pdf/echarts
文章目录Django实践-06导出excel/pdf/echartsDjango实践-06导出excel/pdf/echarts导出excel安装依赖库修改views.py添加excel导出函数修改urls.py添加excel/运行测试导出pdf安装依赖库修改views.py添加pdf导出函数修改urls.py添加pdf/生成前端统计图表修改views.py添加get_teac…...

java并发入门(一)共享模型—Synchronized、Wait/Notify、pack/unpack
一、共享模型—管程 1、共享存在的问题 1.1 共享变量案例 package com.yyds.juc.monitor;import lombok.extern.slf4j.Slf4j;Slf4j(topic "c.MTest1") public class MTest1 {static int counter 0;public static void main(String[] args) throws InterruptedEx…...

Ast2500增加用户自定义功能
备注:这里使用的AMI的开发环境MegaRAC进行AST2500软件开发,并非openlinux版本。1、添加上电后自动执行的任务在PDKAccess.c中列出了系统启动过程中的所有任务,若需要添加功能,在相应的任务中添加自定义线程。一般在两个任务里面添…...

用Python暴力求解德·梅齐里亚克的砝码问题
文章目录固定个数的砝码可称量重量砝码的组合方法40镑砝码的组合问 一个商人有一个40磅的砝码,由于跌落在地而碎成4块。后来,称得每块碎片的重量都是整磅数,而且可以用这4 块来称从1 至40 磅之间的任意整数磅的重物。问这4 块砝码片各重多少&…...

离散Hopfield神经网络的分类——高校科研能力评价
离散Hopfield网络离散Hopfield网络是一种经典的神经网络模型,它的基本原理是利用离散化的神经元和离散化的权值矩阵来实现模式识别和模式恢复的功能。它最初由美国物理学家John Hopfield在1982年提出,是一种单层的全连接神经网络,被广泛应用于…...
- Call逻辑分析和扩展机制)
Retrofit核心源码分析(三)- Call逻辑分析和扩展机制
在前面的两篇文章中,我们已经对 Retrofit 的注解解析、动态代理、网络请求和响应处理机制有了一定的了解。在这篇文章中,我们将深入分析 Retrofit 的 Call 逻辑,并介绍 Retrofit 的扩展机制。 一、Call 逻辑分析 Call 是 Retrofit 中最基本…...

源码分析spring如和对@Component注解进行BeanDefinition注册的
Spring ioc主要职责为依赖进行处理(依赖注入、依赖查找)、容器以及托管的(java bean、资源配置、事件)资源声明周期管理;在ioc容器启动对元信息进行读取(比如xml bean注解等)、事件管理、国际化等处理;首先…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

认识CMake并使用CMake构建自己的第一个项目
1.CMake的作用和优势 跨平台支持:CMake支持多种操作系统和编译器,使用同一份构建配置可以在不同的环境中使用 简化配置:通过CMakeLists.txt文件,用户可以定义项目结构、依赖项、编译选项等,无需手动编写复杂的构建脚本…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

32位寻址与64位寻址
32位寻址与64位寻址 32位寻址是什么? 32位寻址是指计算机的CPU、内存或总线系统使用32位二进制数来标识和访问内存中的存储单元(地址),其核心含义与能力如下: 1. 核心定义 地址位宽:CPU或内存控制器用32位…...
