Lecture4 反向传播(Back Propagation)
目录
1 问题背景
1.1计算图(Computational Graph)
1.2 激活函数(Activation Function)引入
1.3 问题引入
2 反向传播(Back Propagation)
2.1 为什么要使用反向传播
2.2 前馈运算(Forward Propagation)过程
2.3 反向传播过程
2.3.1 计算过程
2.3.2 课堂练习
3 在Pytorch中进行前馈和反向传播计算
3.1 Tensor数据类型
3.2 代码实现
3.2.1 实现线性模型
1 问题背景
1.1计算图(Computational Graph)
计算图(Computational Graph)是一种用于表示数学运算的图形模型。在计算图中,每个节点代表一个数学运算,而每条边代表运算之间的输入输出关系。
计算图用于记录和组织复杂的数学运算,可以帮助我们快速理解运算的依赖关系和结构。在机器学习和深度学习中,计算图是一种常用的工具,用于定义和计算模型的损失函数和梯度。
计算图还可以用于求导,通过利用计算图上的梯度进行反向传播,可以快速计算模型的损失函数对于每个参数的导数。因此,计算图不仅提高了计算效率,而且可以方便地实现自动微分和反向传播。
比如下式

用计算图表示
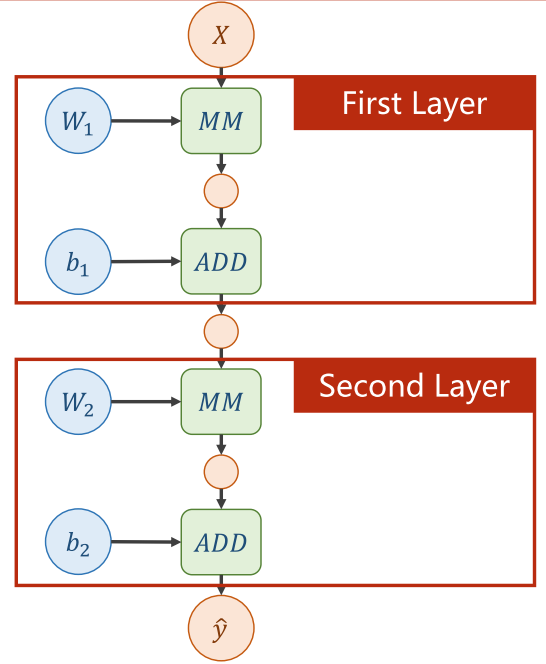
注:MM表示相乘
1.2 激活函数(Activation Function)引入
对于刚刚举例的神经网络计算图,计算机会直接对其进行简化:
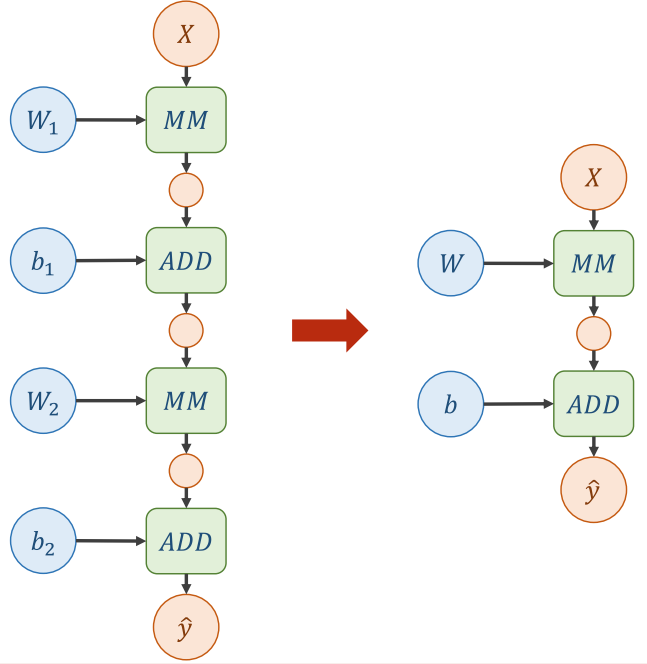
这就导致了计算过程中添加的新的权重值变得毫无意义,层数的划分变得多余,导致神经网络的表示能力下降。
为了解决这个问题,我们需要在每一层的输出处应用上一个非线性变换函数(Nonlinear
Function),这样模型就不会被简化了

如果一个神经网络只使用线性变换函数,那么其最终的表示能力仍然有限,因为它们的输出结果是线性的,无法对复杂的数据进行分类或回归。因此,在每一层的输出都应用非线性变换函数,以增强神经网络的表示能力。
非线性变换函数通常也称为激活函数(Activation Function)。常见的激活函数有Sigmoid函数、ReLU函数等。
补充
线性函数与非线性函数的简单区别:线性函数其函数图像是一条直线;非线性函数的函数图像是一条曲线,等等。
1.3 问题引入
对于一个简单线性模型 ,我们可以利用解析式来进行简单的计算。

通过计算图,我们可以直观地看出计算的过程:
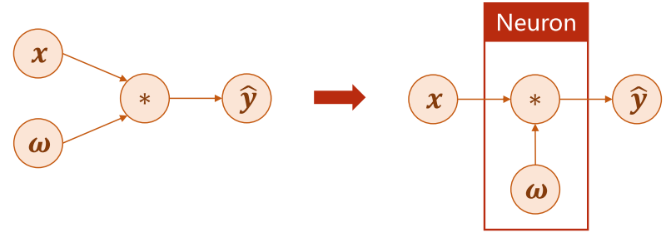
然后利用解析式来更新权重:

但是对于复杂的神经网络模型来说,可能同时含有多个𝜔,如果为每个𝜔写解析式来计算,任务会非常繁重,且解析式也会变得很复杂:
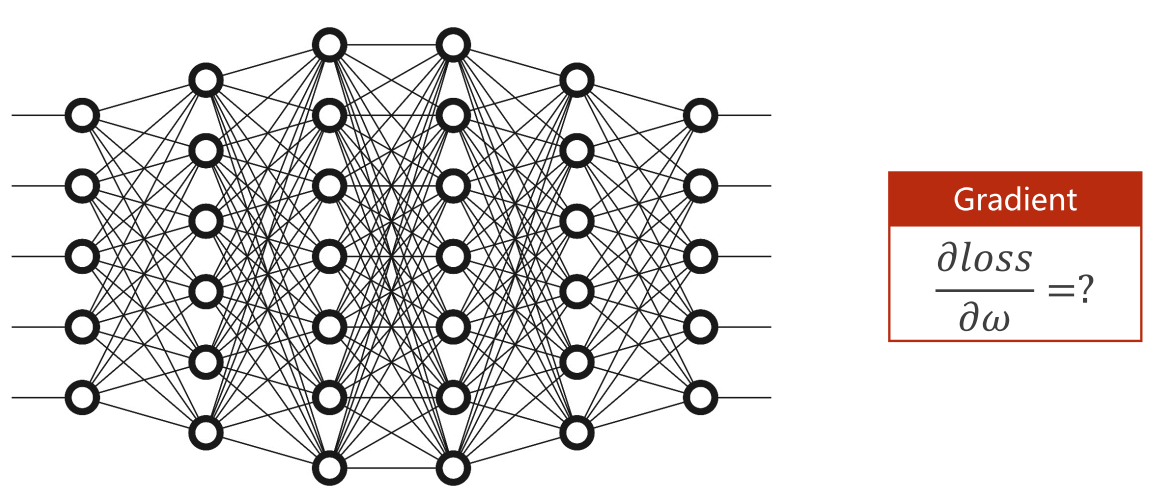
复杂的神经网络模型往往具有大量的权重,如果使用手动计算权重导数的方法,这将是一项非常复杂且繁琐的任务。
2 反向传播(Back Propagation)
2.1 为什么要使用反向传播
如果使用手动计算权重导数的方法来计算复杂神经网络模型,将会非常困难。而反向传播(Back Propagation)可以使用链式法则自动计算损失函数对于每个权重的导数,大大减少计算复杂度,使训练神经网络变得更加有效。
除此之外,反向传播还有一个优点:实现最优化,省去了重复求导的步骤,以及更高效地去计算偏导。详情请参考相关链接,这里不展开:
http://t.csdn.cn/igONJ
https://zhuanlan.zhihu.com/p/25081671
2.2 前馈运算(Forward Propagation)过程

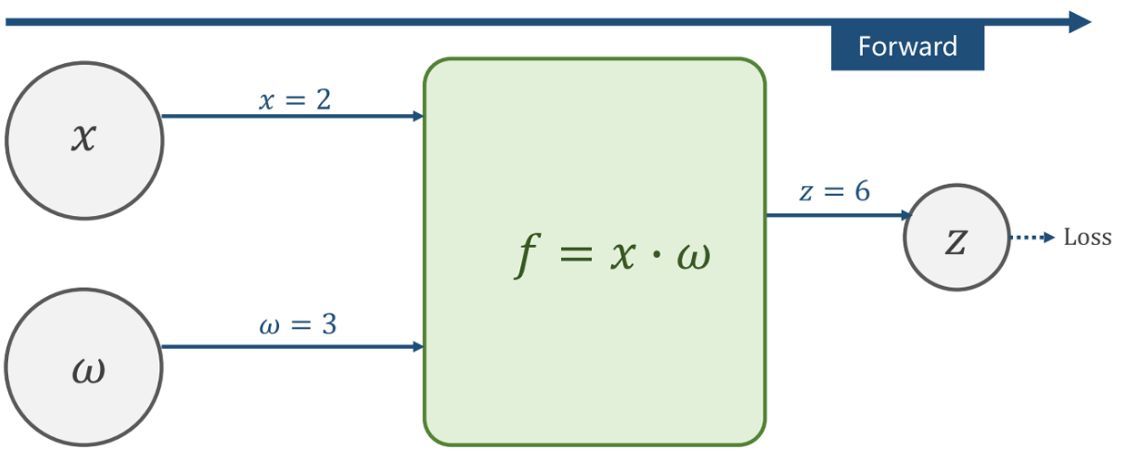
简单来说,就是 x和𝜔进行f(x, 𝜔)操作后得出z,然后把z值应用到Loss中去。
比如𝑓 = 𝑥 ∙ 𝜔, 𝑥 = 2, 𝜔 = 3
2.3 反向传播过程
2.3.1 计算过程

其中以下两个局部函数是由z=𝑥 ∙ 𝜔,分别对x和对𝜔求导得到的:
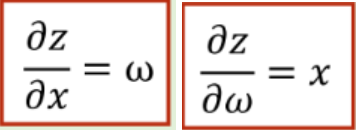
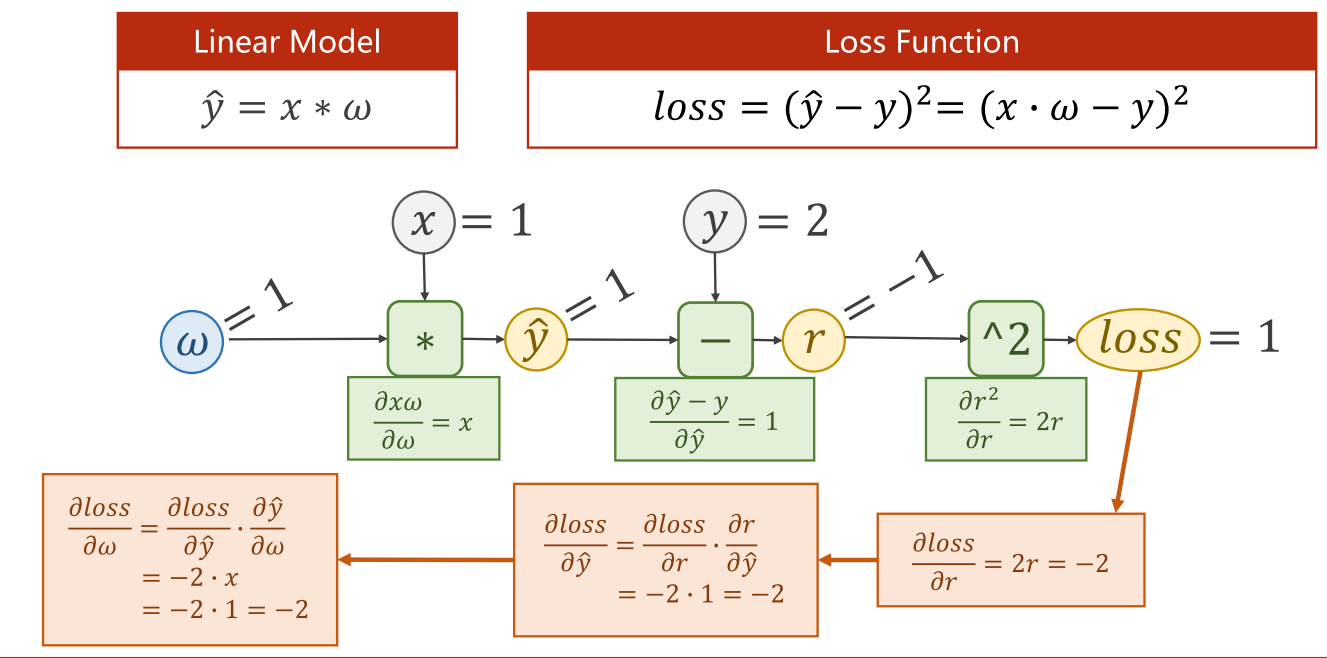
简单来说,就是沿着正方向相反的方向,为每个节点乘上局部导数后,再传递给下一个节点。
2.3.2 课堂练习
(1)计算梯度
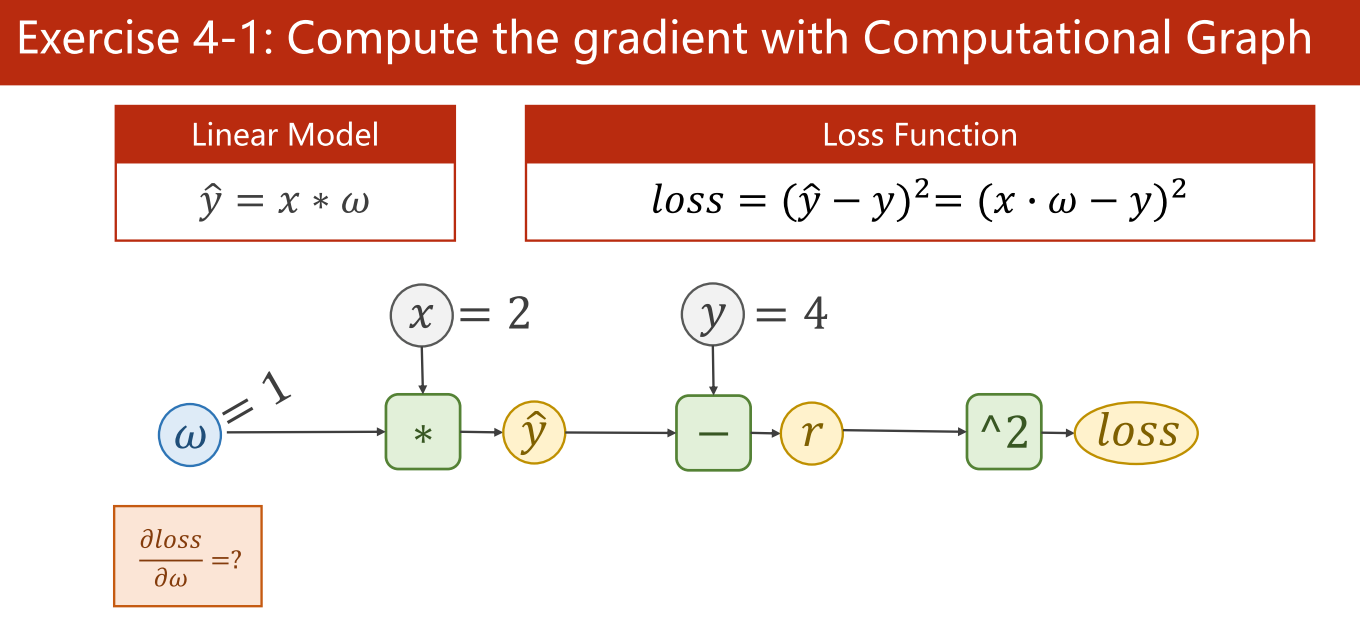
答案:-8
(2)计算加上偏差值后的梯度(计算仿射模型的梯度)
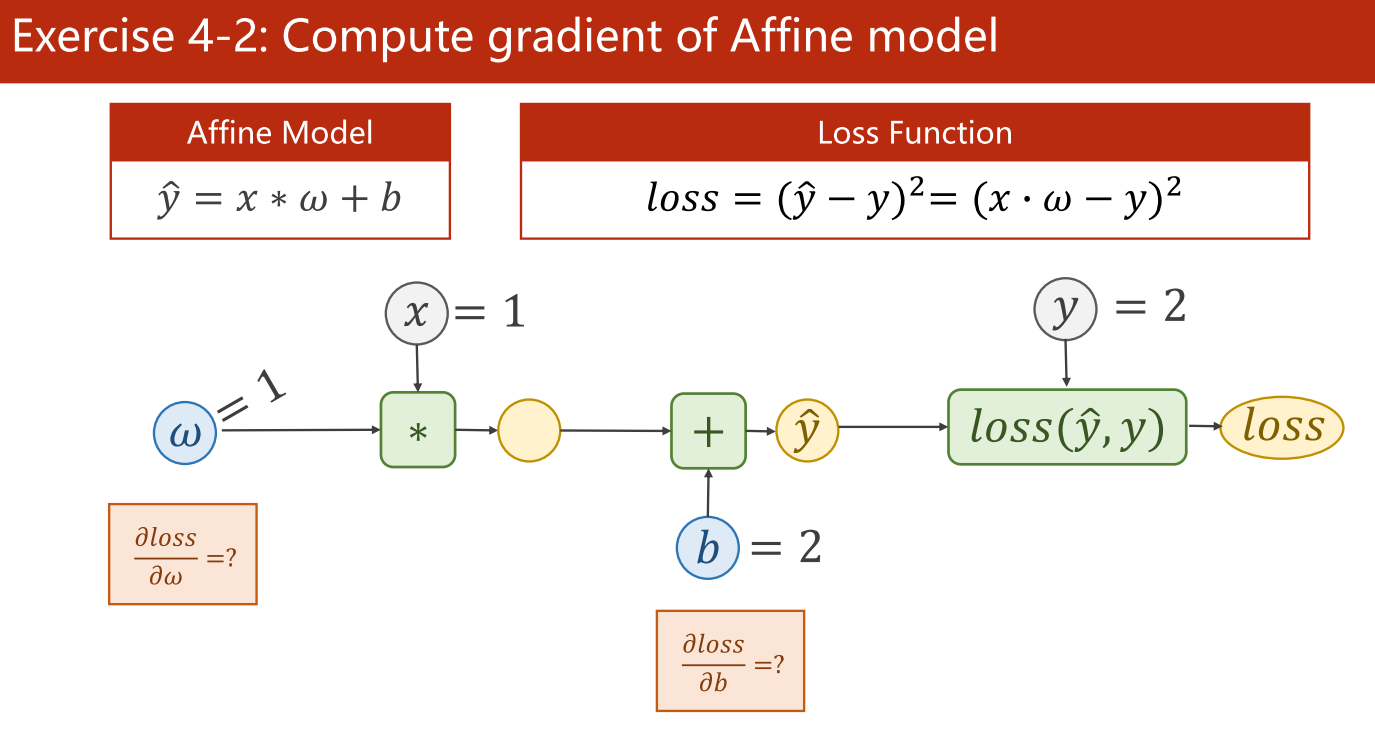
答案:2,2
3 在Pytorch中进行前馈和反向传播计算
3.1 Tensor数据类型

3.2 代码实现
3.2.1 实现线性模型
课堂上的案例,补充了些解释:
import torchx_data = [2.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]
w = torch.Tensor([1.0]) # 创建了一个一维张量,包含单一数值1.0,作为权重初始值
w.requires_grad = True # w=torch.Tensor([1.0])创建了一个张量,然后使用 w.requires_grad = True设置该张量需要求导,于是PyTorch 会记录对该张量的操作,以便在反向传播时进行梯度更新def forward(x):return x * w # 注意这里的x已经自动转换为Tensor类型,原本是list类型def loss(x, y):y_pred = forward(x)return (y_pred - y) ** 2print("predict (before training)", 4, forward(4).item())
for epoch in range(100):for x, y in zip(x_data, y_data):l = loss(x, y)# 反向传播,这句还可以清空释放计算图,避免计算图堆砌在内存中。# 若在当前backward()后,不执行forward() 而是执行另一个backward(),# 则需要在当前backward()时,指定保留计算图,backward(retain_graph)# 换言之,想要保留计算图,则写成backward(retain_graph)l.backward()# 使用item将一个张量转换成一个 Python标量,也是为了防止产生计算图# 一般在进行数学运算时使用grad.data,而在输出梯度数值时使用grad.item()# 一般梯度只有一个元素,所以使用.item()# 可以方便地把梯度值转换为一个数字。print('\tgrad:', x, y, w.grad.item())# 这句代码用来更新权重# 这里使用w.grad.data而不是w.grad是为了防止建立计算图,我们只是对数值做修改,而不是对模型做出修改# 虽然w.data 也是 tensor 类型的数据,# 但它是不需要 gradient 的,因此不会建立计算图,只是在数值范围上发生变化w.data = w.data - 0.01 * w.grad.dataw.grad.data.zero_() # 每次反向传播前,需要清空梯度缓存,以避免之前的梯度对当前梯度造成影响。print("progress:", epoch, l.item()) # 轮数,每轮训练完后对应的loss值,l是tensor类型,所以用item取出值来
print("predict (after training)", 4, forward(4).item())简单来说,每一轮,数据都会先前馈运算出loss,再反向运算出新的梯度,然后用梯度来更新权重值。
相关文章:

Lecture4 反向传播(Back Propagation)
目录 1 问题背景 1.1计算图(Computational Graph) 1.2 激活函数(Activation Function)引入 1.3 问题引入 2 反向传播(Back Propagation) 2.1 为什么要使用反向传播 2.2 前馈运算(Forward Propagation…...
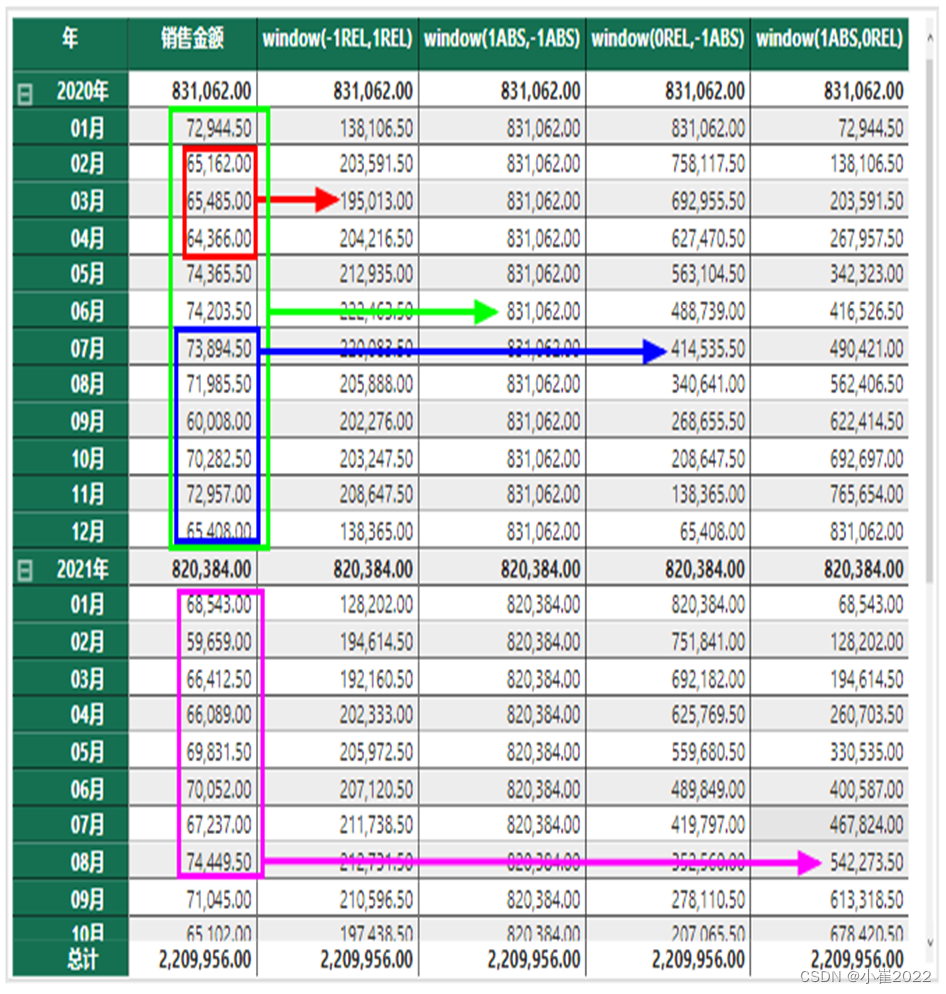
Power BI 筛选器函数---Window实例详解
一、Window函数 语法: Window ( <起始位置>,<起始位置类型>,<结束位置>,<结束位置类型>, [<关系>], [<OrderBy>],[空白],[PartitionBy] ) 含义: 对指定分区(PartitioinBy)中的行(关系表&…...

基础篇—如何创建css样式表,并集成到html文件中?
CSS 创建 HTML相当于一个页面的结构,CSS相当于页面的装饰,浏览器当读到一个样式表时,浏览器会根据它来格式化 HTML 文档。 如何插入样式表 插入样式表的方法有三种: 外部样式表(External style sheet)内部样式表(Internal style sheet)内联样式(Inline style)1、外…...

WindowsServer服务器系列:部署FTP文件服务
1、点击“开始”菜单,选择“服务器管理器” 2、在接下来弹出页面中选择“添加角色和功能” 3、接下来点击“下一步” 4、接下来选择“基于角色或基于功能的安装”并点击“下一步” 5、选择“从服务器池中选择服务器”并点击“下一步” 6、接下来选中“Web 服务器(II…...
| 真题+思路+代码)
华为OD机试 - 数字加减游戏(Python)| 真题+思路+代码
数字加减游戏 题目 小明在玩一个数字加减游戏,只使用加法或者减法,将一个数字 s 变成数字 t。 每个回合,小明可以用当前的数字加上或减去一个数字。 现在有两种数字可以用来加减,分别为 a,b(a!=b),其中 b 没有使用次数限制。 请问小明最少可以用多少次 a,才能将数字 s …...

【c/c++】c语言的自增操作在不同编译器的差别
示例代码 代码如下: #include <stdio.h>#define product(x) ((x)*(x))int main(void) {int i 3, j, k;j product(i); // (i) * (i)k product(i); // (i) * (i)printf("%d %d\n", j, k); }执行结果 在Ubuntu18.04下通过GCC编译和执行的结果…...
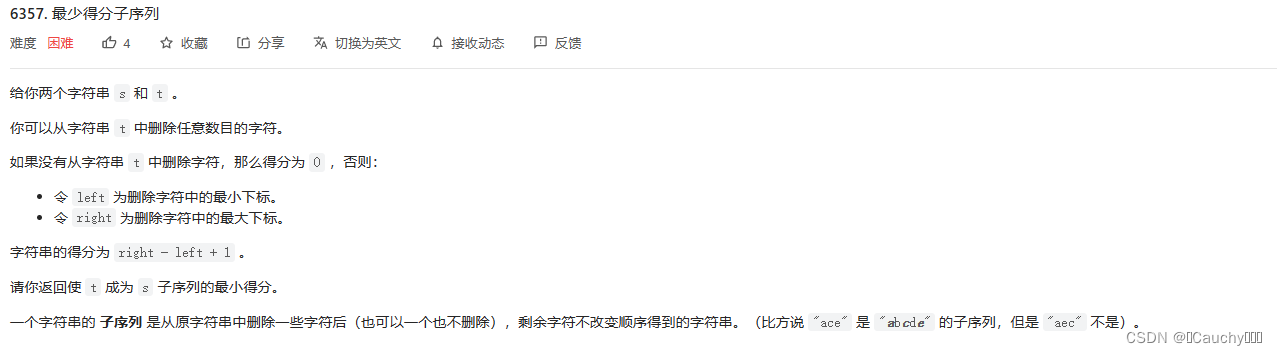
【LeetCode第 332 场周赛】
传送门 文章目录6354. 找出数组的串联值6355. 统计公平数对的数目6356. 子字符串异或查询6357. 最少得分子序列6354. 找出数组的串联值 题目 思路 前后指针 代码 class Solution { public:long long findTheArrayConcVal(vector<int>& nums) {long long res 0;i…...
【蓝桥杯单片机】Keil5中怎么添加STC头文件;从烧录软件中添加显示添加成功后新建工程时依旧找不到
蓝桥杯单片机的芯片型号:IAP15F2K61S2 添加头文件:STC15F2K60S2.H 【1】如何通过烧录软件添加STC头文件: 从ATC-ISP的Keil仿真设置中添加(同时自动下载仿真驱动)仔细阅读添加说明 KEIL5添加STC芯片库_Initdev的博客-…...
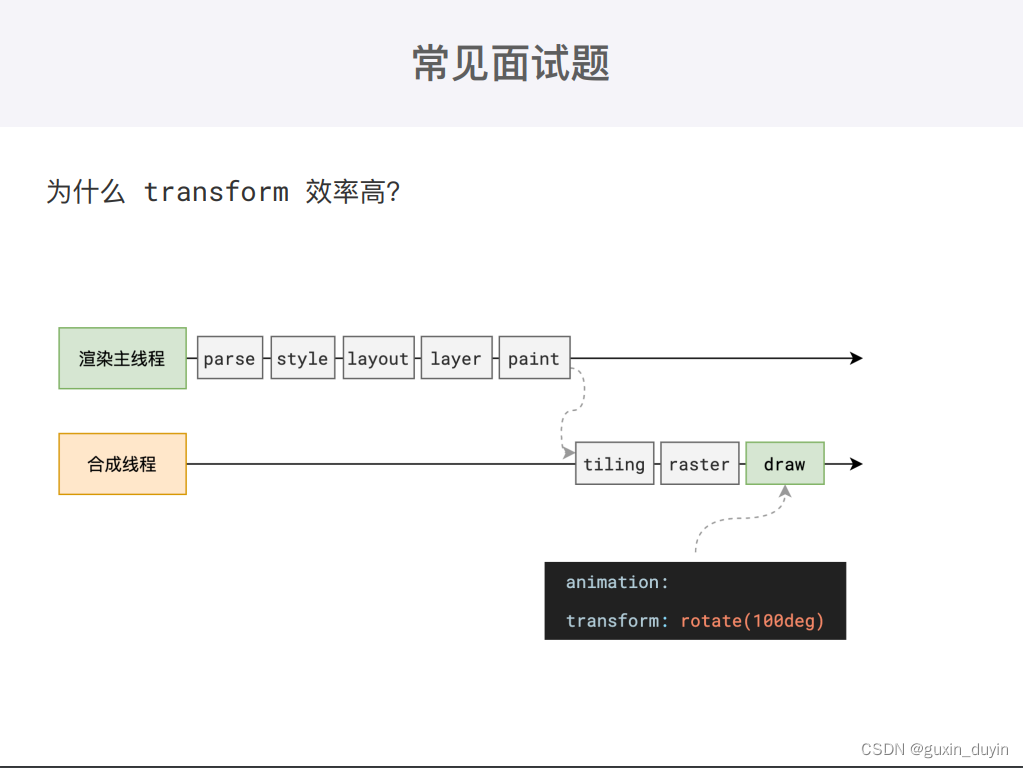
图解浏览器渲染页面详细过程
渲染详细过程 产生渲染任务,开启渲染流程 当浏览器的网络线程收到 HTML 文档后,会产生一个渲染任务,并将其传递给渲染主线程的消息队列。 在事件循环机制的作用下,渲染主线程取出消息队列中的渲染任务,开启渲染流程。…...
)
多线程面试题开胃菜1(5道)
一.多线程有什么用?1)发挥多核CPU 的优势随着工业的进步,现在的笔记本、台式机乃至商用的应用服务器至少也都是双核的,4 核、8 核甚至 16 核的也都不少见,如果是单线程的程序,那么在双核 CPU 上就浪费了 50…...
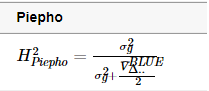
植物育种中广义遗传力的定义
大家好, 我是邓飞。 今天聊一下广义遗传力的计算方法。 广义遗传力定义 广义遗传力(H2H^2H2)定义为归因于基因型总体遗传变异的表型变异比例。 通常他包括三个解释:(详见我这篇博客的公式推导 回归系数 相关系数 遗…...

西瓜书读书笔记—绪论
文章目录机器学习典型的机器学习过程基本术语归纳偏好机器学习 机器学习:致力于研究如果通过计算的手段,利用经验来改善系统自身的性能 在计算机系统中,“经验” 通常以 “数据” 形式存在,因此,机器学习所研究的主要内…...

ES8——Generator函数的使用
babel工具插件下载:npm i --save babel-polyfill 引入:polyfill.js进行转码(es8->es5) 介绍 Generator函数用于生成迭代器 function * (){} yeild: 作用同return类似 {const obj function* () {yield "a";yield 12…...

德馨食品冲刺A股上市:计划募资9亿元,林志勇为实际控制人
近日,浙江德馨食品科技股份有限公司(下称“德馨食品”或“德馨饮料”)预披露更新招股书,准备在上海证券交易所主板上市。据贝多财经了解,德馨食品于2022年7月5日递交上市申请,安信证券为其保荐机构。 本次…...

湿敏电阻的原理,结构,分类与应用总结
🏡《总目录》 0,概述 湿敏电阻是指电阻值随着环境的湿度变化而变化的电阻,本文对其工作原理,结构,分类和应用场景进行总结。 1,工作原理 湿敏电阻是利用湿敏材料制成的,湿敏材料吸收空气中水分时,自身的阻值发生变化。 2,结构 如下图所示,市民电阻包括4个部分构成,…...

千锋教育嵌入式物联网教程之系统编程篇学习-03
目录 进程的终止 exit函数 _exit函数 进程退出清理 进程间的替换 进程间通信 常见通信机制 进程间通信的实质 信号 产生信号的方式 信号的默认处理方式 进程对信号的处理方式 kill函数 进程的终止 使用exit函数对进程进行终止,而return只是结束函数&a…...
升级到https
现在很多站长都会考虑将自己的站点从http升级到https,不仅是基于安全的考虑,有的也是因为第三方平台的限制,如谷歌浏览器会将http站点标记为不安全的站点,微信平台要求接入的微信小程序必须使用https等。 那如何将一个http站点升…...
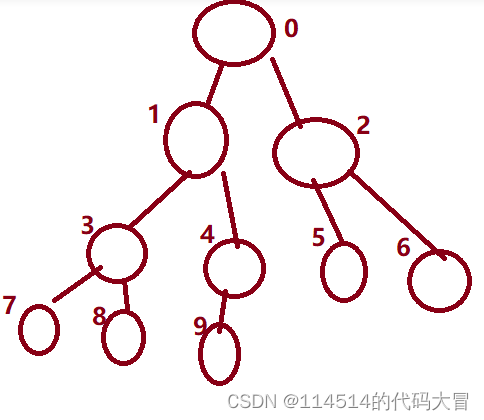
【C语言】数据结构-二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...

c++中std::condition_variable最全用法归纳
前言 建议阅读以下文章前需先对建立 std::thread 多线程与std::mutex 锁有一定程度的熟悉 std::thread最全用法归纳 std::mutex最全用法归纳 概括 使用 std::condition_variable 的 wait 会把目前的线程 thread 停下来并且等候事件通知,而在另一个线程中可以使用…...

Python数据可视化:数据关系图表可视化
目录 1、散点图 1.1、趋势显示的二维散点图 1.2、分布显示的二维散点图 1.3、散点曲线图...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...
