【C语言】数据结构-二叉树
主页:114514的代码大冒险
qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ )
Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com
引入
我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树
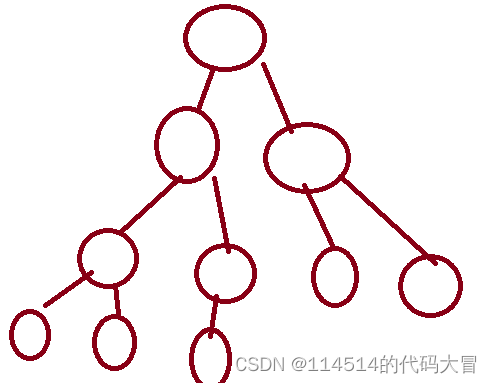
望文生义,这个数据结构肯定与现实中的树, 有着一定的联系,如图:
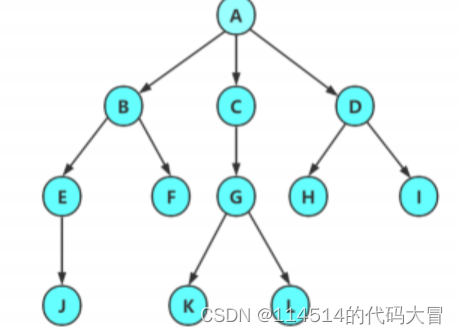

数据结构中的树它看起来像树枝,也想树的根部
树的概念

树的相关概念
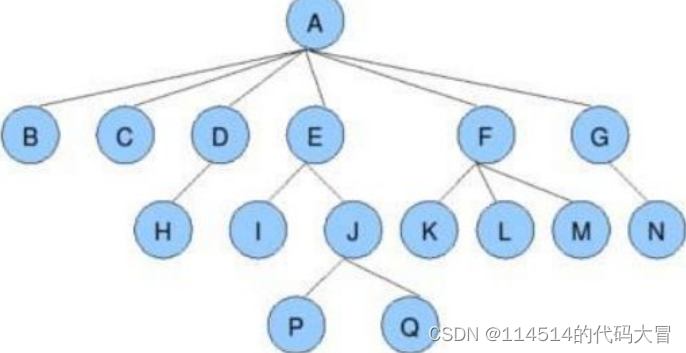
节点的度:一个节点含有的子树的个数称为该节点的度;如上图:A的为6叶节点或终端节点:度为0的节点称为叶节点;如上图:B、C、H、I...等节点为叶节点非终端节点或分支节点:度不为0的节点;如上图:D、E、F、G...等节点为分支节点双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点;如上图:A是B的父节点孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点;如上图:B是A的孩子节点兄弟节点:具有相同父节点的节点互称为兄弟节点;如上图:B、C是兄弟节点树的度:一棵树中,最大的节点的度称为树的度;如上图:树的度为6节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;树的高度或深度:树中节点的最大层次;如上图:树的高度为4堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙森林:由m(m>0)棵互不相交的树的集合称为森林;
树的表示
概念图:

树在实际中的运用(表示文件系统的目录树结构)
文件目录:

公司内部功能安排
二叉树(特殊的树)
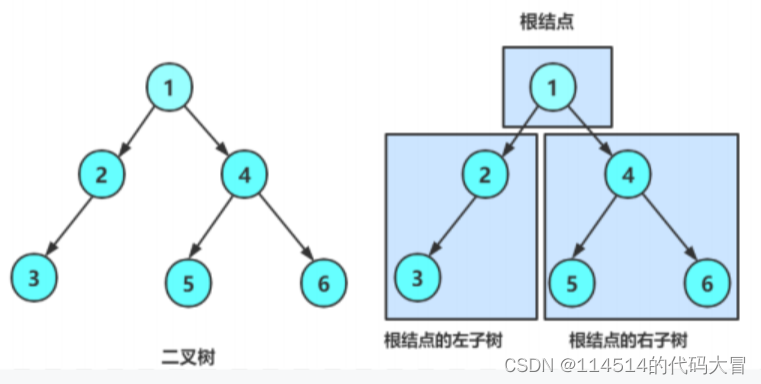

这些都不重要
你只需要知道二叉树的每个节点最多两个孩子
可以没有孩子,也可以只有一个孩子
另外在二叉树中
左孩子和右孩子是有差异的
现实中的二叉树


1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是说,如果一个二叉树的层数为K,且结点总数是2^k-1,则它就是满二叉树。
2. 完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
说人话:
就是说如果除了最底下那一排(所谓的叶子节点)其他的节点都有两个孩子
我们就称之为满二叉树

那么什么是完全二叉树呢
就是除了树的倒数第二排之外,其他节点都有两个孩子
如图: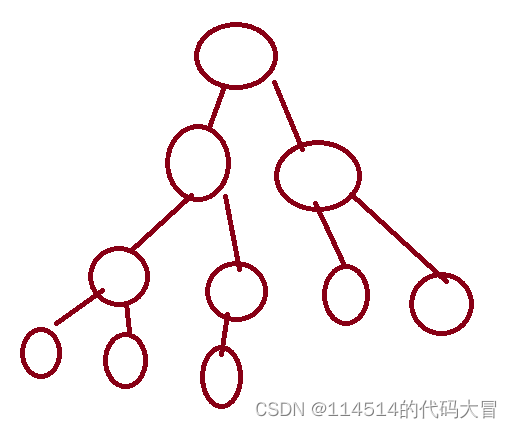
二叉树的性质


说了一大堆,能看懂多少算多少
我来说几个比较可能用到的点
 只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
只要是树,有两个孩子的节点始终比没有孩子的节点的数量少一
完全二叉树的坐标规律如右图所示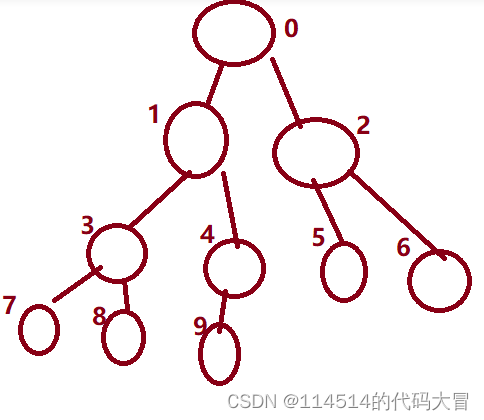
(完全二叉树中) 我们假使某节点这个下标为i,那么它的父亲就是
(i-1)/2 ,左孩子(如果有的话)为2*i+1,右孩子为左孩子坐标加1
另外还有就是这个完全二叉树的层数问题
除开最后一层外,第一层节点的数量为2^0,第二次为2^1第三次为2^2
第n层为2^(n-1),
如此满二叉树的节点数量为2^n - 1个
hhh,非满二叉树的节点数量则为前n-1层的节点数量+最后一层的节点数
我想,这个时候,在知道二叉树的节点的数量前提下
求出二叉树的深度,也就是层数不是什么困难的事情了
总结
这就是今天的树的概念讲解
这部分内容不需要太过焦虑
这些概念现在只是稍微有个大概就可以
我们在接下来的学习中会反复提到
相关文章:

【C语言】数据结构-二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...

c++中std::condition_variable最全用法归纳
前言 建议阅读以下文章前需先对建立 std::thread 多线程与std::mutex 锁有一定程度的熟悉 std::thread最全用法归纳 std::mutex最全用法归纳 概括 使用 std::condition_variable 的 wait 会把目前的线程 thread 停下来并且等候事件通知,而在另一个线程中可以使用…...

Python数据可视化:数据关系图表可视化
目录 1、散点图 1.1、趋势显示的二维散点图 1.2、分布显示的二维散点图 1.3、散点曲线图...

Urho3D约定
Urho3D使用以下约定和原则: 左手坐标系。正X、Y和Z轴指向右侧、上方和前方,正旋转为顺时针。度用于角度。顺时针顶点定义正面。音频音量指定为0.0(静音)到1.0(全音量)路径名使用斜杠而不是反斜杠。调用操作…...

python数据结构-列表,元组
列表 列表是Python中最通用的数据类型,可以写成方括号之间的逗号分隔值(项目)列表。 使用列表的重要事项是,列表中的项目不必是相同的类型。也就是说一个列表中的项目(元素)可以是数字,字符串,数组,字典等甚至是列表类…...
Properties类读配置文件、修改配置文件
Properties类简介(1)Properties类是专门用于读写配置文件的集合类(2)配置文件的后缀名为.properties,内容格式为:# 可以用“#”作为注释 键值 键值**注意:**键值对不需要有空格,值不需要用引号一起来。默认类型是String。键、值不可以是null(3)Properties类的方法可查找api文档…...
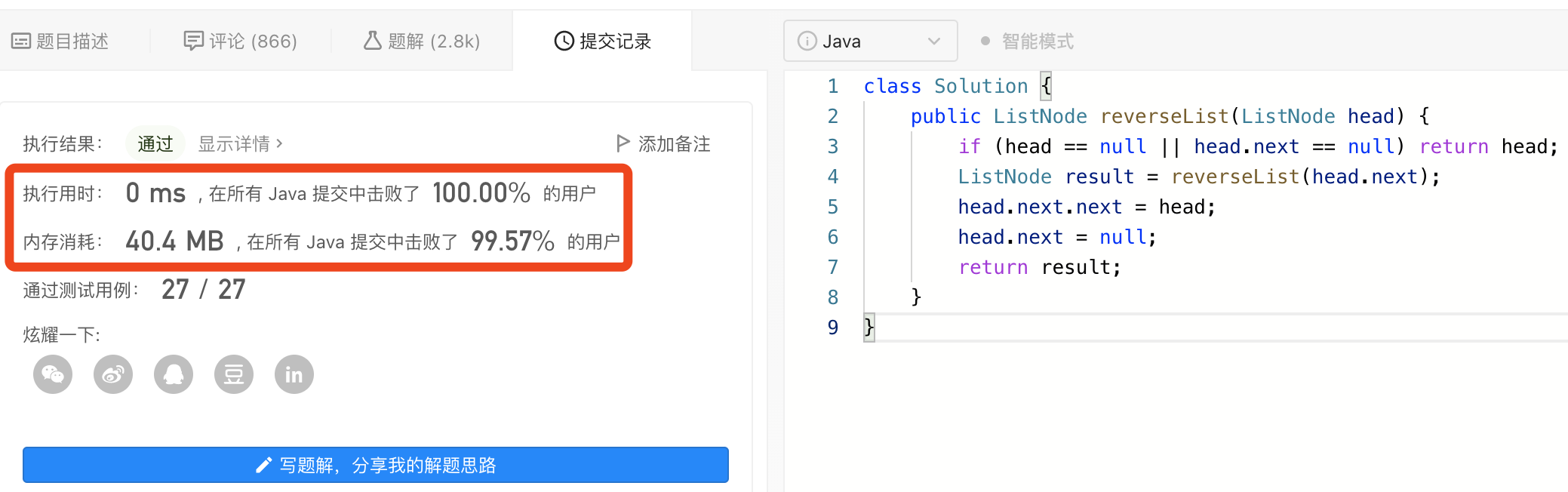
图解LeetCode——剑指 Offer 24. 反转链表
一、题目 定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。 二、示例 示例: 【输入】 1->2->3->4->5->NULL 【输出】 5->4->3->2->1->NULL 限制: 0 < 节点个数 < 5000 三、…...

【C语言】“指针的运算”、“指针与数组”
文章目录一、指针运算1.指针 - 整数2.指针-指针3.指针关系运算二、指针与数组三、二级指针四、指针数组完结一、指针运算 指针可以进行整数,指针-指针,还有关系运算,其他的运算会被编译器阻止。 1.指针 - 整数 对指针进行的时候一定要注意不…...
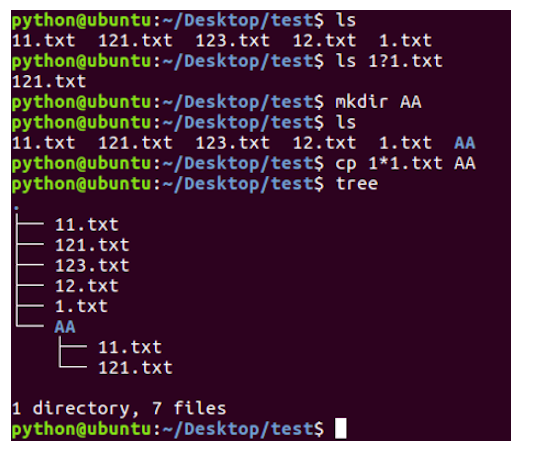
Linux高级命令之查找文件命令
查找文件命令学习目标能够说出查找文件使用的命令1. find命令及选项的使用命令说明find在指定目录下查找文件(包括目录)find命令选项:选项说明-name根据文件名(包括目录名)字查找find命令及选项的效果图:2. find命令结合通配符的使用通配符:是一种特殊语句,主要有星…...

PyCharm+Docker:打造最舒适的深度学习炼丹炉
九、PyCharmDocker:打造最舒适的深度学习炼丹炉 安装docker: 如何在 Ubuntu 22.04 LTS 中安装 Docker 和 Docker Compose https://zhuanlan.zhihu.com/p/547169542 修改Linux硬盘卷标: ntfs文件系统:https://blog.csdn.net/n…...
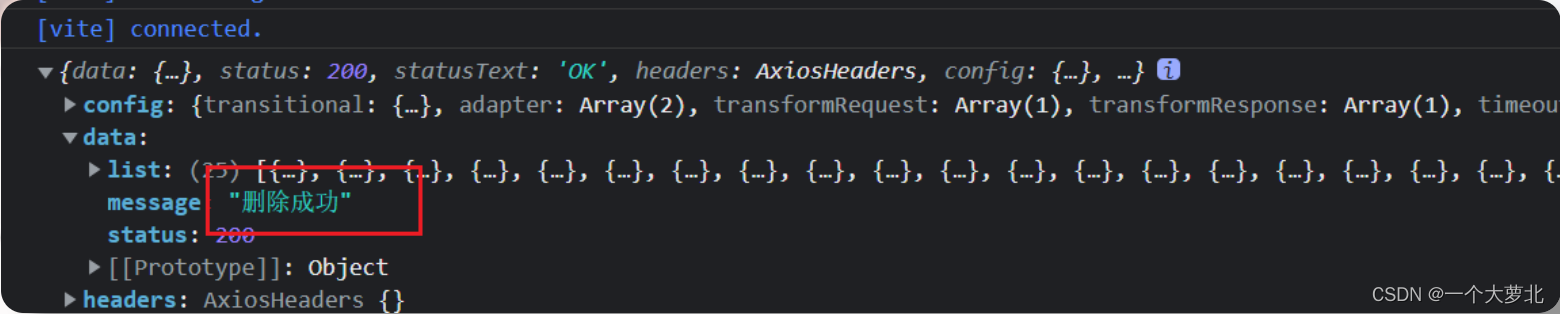
【mock】手把手带你用mock写自定义接口+mock常用语法
mock自定义接口完整流程 官网语法规范:https://github.com/nuysoft/Mock/wiki/Syntax-Specification 首先: 要有一个项目,我这里是vue3项目,以下从vue3项目搭建开始,已搭建好的请直接看2 1.空目录下新建vue3项目 运行创建项目命令: 在bash中:(文件路径处输入cm…...

2023 年腾讯云服务器CVM快速配置购买教程,新手上云必备!
腾讯云服务器快速配置购买教程是新手必备的上云教程。主机教程网在本文中以腾讯云服务器为例,给大家带来一个完整的、手把手教学的服务器购买流程。助力快速完成服务器的购买、配置、以及网站的搭建,给新手节省宝贵的时间,避免采坑࿰…...

opencv显示图像
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

C++:类和对象(中)
文章目录1 类的6个默认成员函数2 构造函数2.1 概念2.2 特性3 析构函数3.1 概念3.2 特性4 拷贝构造函数4.1 概念4.2 特性5 赋值运算符重载5.1 运算符重载5.2 赋值运算符重载5.3 前置重载和后置重载6 日期类的实现7 const成员8 取地址及const取地址操作符重载1 类的6个默认成员函…...
53. 最大子数组和
文章目录题目描述暴力法动态规划法分治法参考文献题目描述 给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。 子数组 是数组中的一个连续部分。 示例 1: 输入&…...

基于Java+SpringBoot+SpringCloud+Vue前后端分离医院管理系统设计与实现
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建、毕业项目实战、项目定制✌ 博主作品:《微服务实战》专栏是本人的实战经验总结,《S…...

QT基础入门【环境配置篇】linux桌面QT开发环境的构建以及问题解决
目录 一、下载QT的安装包 二、安装 1.执行以下命令开始安装 2.选择配置 三、启动...

Linux系统之部署企业内部静态导航页
Linux系统之部署企业内部静态导航页 一、本次实践目的二、检查本地系统环境1.检查系统版本2.检查内核版本三、下载静态导航页资源包1.创建下载目录2.下载资源包四、安装apache服务1.安装httpd2.复制网页文件3.重启httpd服务4.检查httpd服务状态五、访问导航页六、修改导航页网站…...
)
2023备战金三银四,Python自动化软件测试面试宝典合集(四)
接上篇:11、点击塞钱进红包,选择使用新卡付款,按照流程添加新卡,此时同样需要考虑金额>新卡余额,金额<新卡余额,金额新卡余额三种情况12、使用指纹确认付款(正确的/不正确的指纹)13、使用密码确认付款…...

算法训练营 day43 动态规划 不同路径 不同路径 II
算法训练营 day43 动态规划 不同路径 不同路径 II 不同路径 62. 不同路径 - 力扣(LeetCode) 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器人每次只能向下或者向右移动一步。机器人试图达…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

LabVIEW双光子成像系统技术
双光子成像技术的核心特性 双光子成像通过双低能量光子协同激发机制,展现出显著的技术优势: 深层组织穿透能力:适用于活体组织深度成像 高分辨率观测性能:满足微观结构的精细研究需求 低光毒性特点:减少对样本的损伤…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

