植物育种中广义遗传力的定义
大家好, 我是邓飞。
今天聊一下广义遗传力的计算方法。
广义遗传力定义
广义遗传力(H2H^2H2)定义为归因于基因型总体遗传变异的表型变异比例。
通常他包括三个解释:(详见我这篇博客的公式推导 回归系数 相关系数 遗传力的关系)
- (i)它相当于观察到的表型上不可观察的基因型值的线性回归的确定系数;
- (ii)也是预测表型值和基因型值之间的相关系数的平方;
- (iii)它表示可以实现为选择响应(RR)的选择差异(SS)的比例(Falconer和Mackay,2005)。
有两个主要原因说明植物育种中对输入平均值的遗传力感兴趣(Schmidt等人,2019a):
-
1,计算这个参数,可以帮育种家预测选择相应
-
2,这是一种用于评估品种评估试验结果的有用性和准确性的描述性度量。
2,One stage和Two stage
Two stage,两阶段方法,就是先计算单个地点的育种值,然后再计算一年多点或者多年多点的数据,这里多个年份或者多个地点,都看做是不同的环境。One stage是一步到位的MET的分析方法,可以是一年多点,或者是多年多点,都在一个模型中进行分析。
2.1 Two stage
yikt=μ+Gi+Et+GxEit+εikty_{ikt} = μ + G_i+E_t+GxE_{it}+ε_{ikt}yikt=μ+Gi+Et+GxEit+εikt
这里的表型方差组分为:
σp2=σg2+σg∗e2ne+σe2ne∗nr\sigma_p^2 = \sigma_g^2 + \frac{\sigma_{g*e}^2}{n_e} + \frac{\sigma_{e}^2}{n_e*n_r}σp2=σg2+neσg∗e2+ne∗nrσe2
这里的n_e,是环境的个数,n_r是重复的个数。
2.2 One stage
这里,Y是年份,E是地点,公式中包括:
- 基因型
- 年份
- 地点
- 年份与地点互作
- 基因型与年份互作
- 基因型与地点互作
- 基因型与年份与地点互作
- 残差
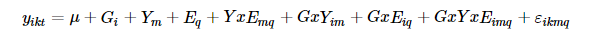
表型方差的计算方法:
每一项,都除以对应的重复数。如果数据有缺失值,用调整均值进行分析,方法参考:
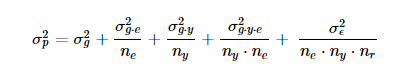
3. 更广义的遗传力计算方法
3.1 标准方法
第一种,标准方法,我们最常用的,Vg/Vp,根据一年多点或者多年多点,计算出表型的方差组分,然后用下面公式计算:
H2=σg2σp2H^2 = \frac{\sigma_g^2}{\sigma_p^2} H2=σp2σg2
3.2 Cullis遗传力计算
第二种,Cullis方法
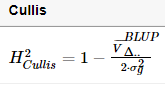
3.3 Piepho遗传力计算
第三种:Piepho方法
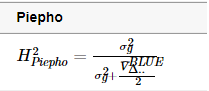
4. 代码数据演示
4.1 标准方法演示
4.2 Cullis遗传力演示
4.3 Piepho遗传力演示
相关文章:
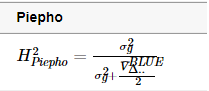
植物育种中广义遗传力的定义
大家好, 我是邓飞。 今天聊一下广义遗传力的计算方法。 广义遗传力定义 广义遗传力(H2H^2H2)定义为归因于基因型总体遗传变异的表型变异比例。 通常他包括三个解释:(详见我这篇博客的公式推导 回归系数 相关系数 遗…...

西瓜书读书笔记—绪论
文章目录机器学习典型的机器学习过程基本术语归纳偏好机器学习 机器学习:致力于研究如果通过计算的手段,利用经验来改善系统自身的性能 在计算机系统中,“经验” 通常以 “数据” 形式存在,因此,机器学习所研究的主要内…...

ES8——Generator函数的使用
babel工具插件下载:npm i --save babel-polyfill 引入:polyfill.js进行转码(es8->es5) 介绍 Generator函数用于生成迭代器 function * (){} yeild: 作用同return类似 {const obj function* () {yield "a";yield 12…...

德馨食品冲刺A股上市:计划募资9亿元,林志勇为实际控制人
近日,浙江德馨食品科技股份有限公司(下称“德馨食品”或“德馨饮料”)预披露更新招股书,准备在上海证券交易所主板上市。据贝多财经了解,德馨食品于2022年7月5日递交上市申请,安信证券为其保荐机构。 本次…...

湿敏电阻的原理,结构,分类与应用总结
🏡《总目录》 0,概述 湿敏电阻是指电阻值随着环境的湿度变化而变化的电阻,本文对其工作原理,结构,分类和应用场景进行总结。 1,工作原理 湿敏电阻是利用湿敏材料制成的,湿敏材料吸收空气中水分时,自身的阻值发生变化。 2,结构 如下图所示,市民电阻包括4个部分构成,…...

千锋教育嵌入式物联网教程之系统编程篇学习-03
目录 进程的终止 exit函数 _exit函数 进程退出清理 进程间的替换 进程间通信 常见通信机制 进程间通信的实质 信号 产生信号的方式 信号的默认处理方式 进程对信号的处理方式 kill函数 进程的终止 使用exit函数对进程进行终止,而return只是结束函数&a…...
升级到https
现在很多站长都会考虑将自己的站点从http升级到https,不仅是基于安全的考虑,有的也是因为第三方平台的限制,如谷歌浏览器会将http站点标记为不安全的站点,微信平台要求接入的微信小程序必须使用https等。 那如何将一个http站点升…...
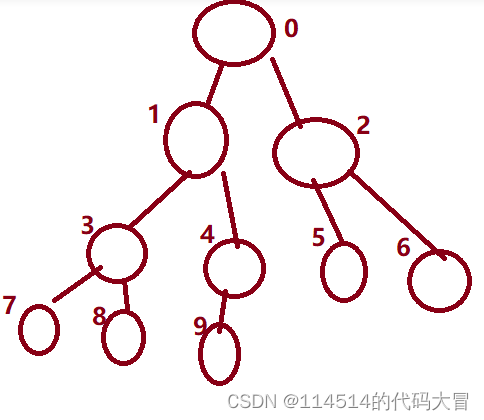
【C语言】数据结构-二叉树
主页:114514的代码大冒险 qq:2188956112(欢迎小伙伴呀hi✿(。◕ᴗ◕。)✿ ) Gitee:庄嘉豪 (zhuang-jiahaoxxx) - Gitee.com 引入 我们之前已经学过线性数据结构,今天我们将介绍非线性数据结构----树 树是一种非线性的…...

c++中std::condition_variable最全用法归纳
前言 建议阅读以下文章前需先对建立 std::thread 多线程与std::mutex 锁有一定程度的熟悉 std::thread最全用法归纳 std::mutex最全用法归纳 概括 使用 std::condition_variable 的 wait 会把目前的线程 thread 停下来并且等候事件通知,而在另一个线程中可以使用…...

Python数据可视化:数据关系图表可视化
目录 1、散点图 1.1、趋势显示的二维散点图 1.2、分布显示的二维散点图 1.3、散点曲线图...

Urho3D约定
Urho3D使用以下约定和原则: 左手坐标系。正X、Y和Z轴指向右侧、上方和前方,正旋转为顺时针。度用于角度。顺时针顶点定义正面。音频音量指定为0.0(静音)到1.0(全音量)路径名使用斜杠而不是反斜杠。调用操作…...

python数据结构-列表,元组
列表 列表是Python中最通用的数据类型,可以写成方括号之间的逗号分隔值(项目)列表。 使用列表的重要事项是,列表中的项目不必是相同的类型。也就是说一个列表中的项目(元素)可以是数字,字符串,数组,字典等甚至是列表类…...
Properties类读配置文件、修改配置文件
Properties类简介(1)Properties类是专门用于读写配置文件的集合类(2)配置文件的后缀名为.properties,内容格式为:# 可以用“#”作为注释 键值 键值**注意:**键值对不需要有空格,值不需要用引号一起来。默认类型是String。键、值不可以是null(3)Properties类的方法可查找api文档…...
图解LeetCode——剑指 Offer 24. 反转链表
一、题目 定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。 二、示例 示例: 【输入】 1->2->3->4->5->NULL 【输出】 5->4->3->2->1->NULL 限制: 0 < 节点个数 < 5000 三、…...

【C语言】“指针的运算”、“指针与数组”
文章目录一、指针运算1.指针 - 整数2.指针-指针3.指针关系运算二、指针与数组三、二级指针四、指针数组完结一、指针运算 指针可以进行整数,指针-指针,还有关系运算,其他的运算会被编译器阻止。 1.指针 - 整数 对指针进行的时候一定要注意不…...
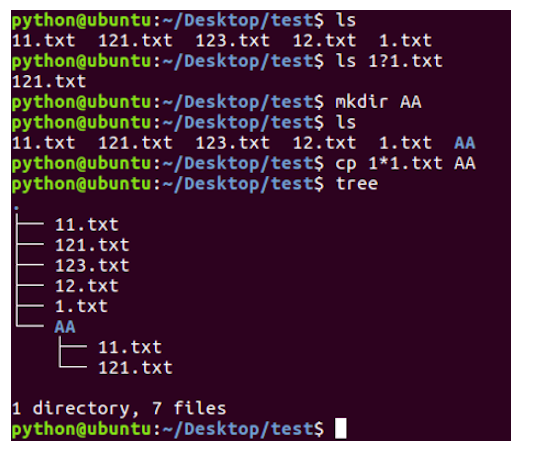
Linux高级命令之查找文件命令
查找文件命令学习目标能够说出查找文件使用的命令1. find命令及选项的使用命令说明find在指定目录下查找文件(包括目录)find命令选项:选项说明-name根据文件名(包括目录名)字查找find命令及选项的效果图:2. find命令结合通配符的使用通配符:是一种特殊语句,主要有星…...

PyCharm+Docker:打造最舒适的深度学习炼丹炉
九、PyCharmDocker:打造最舒适的深度学习炼丹炉 安装docker: 如何在 Ubuntu 22.04 LTS 中安装 Docker 和 Docker Compose https://zhuanlan.zhihu.com/p/547169542 修改Linux硬盘卷标: ntfs文件系统:https://blog.csdn.net/n…...
【mock】手把手带你用mock写自定义接口+mock常用语法
mock自定义接口完整流程 官网语法规范:https://github.com/nuysoft/Mock/wiki/Syntax-Specification 首先: 要有一个项目,我这里是vue3项目,以下从vue3项目搭建开始,已搭建好的请直接看2 1.空目录下新建vue3项目 运行创建项目命令: 在bash中:(文件路径处输入cm…...

2023 年腾讯云服务器CVM快速配置购买教程,新手上云必备!
腾讯云服务器快速配置购买教程是新手必备的上云教程。主机教程网在本文中以腾讯云服务器为例,给大家带来一个完整的、手把手教学的服务器购买流程。助力快速完成服务器的购买、配置、以及网站的搭建,给新手节省宝贵的时间,避免采坑࿰…...

opencv显示图像
大家好,我是csdn的博主:lqj_本人 这是我的个人博客主页: lqj_本人的博客_CSDN博客-微信小程序,前端,python领域博主lqj_本人擅长微信小程序,前端,python,等方面的知识https://blog.csdn.net/lbcyllqj?spm1011.2415.3001.5343哔哩哔哩欢迎关注…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...
