当前位置： 首页 > news >正文

HTML静态网页成品作业(HTML+CSS)——故宫介绍网页(4个页面)

news 2026/2/11 4:15:42

🎉不定期分享源码，关注不丢失哦

文章目录

  • 一、作品介绍
  • 二、作品演示
  • 三、代码目录
  • 四、网站代码
    • HTML部分代码
  • 五、源码获取

一、作品介绍

🏷️本套采用HTML+CSS，未使用Javacsript代码，共有4个页面。

二、作品演示

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

三、代码目录

在这里插入图片描述

四、网站代码

HTML部分代码

<!DOCTYPE html>
<html lang="zh">
<head><meta charset="UTF-8"><meta http-equiv="X-UA-Compatible" content="IE=edge"><meta name="viewport" content="width=device-width, initial-scale=1.0"><title>北京故宫</title><link rel="stylesheet" href="./css/style.css">
</head>
<body><main><div class="logo"><img src="./images/logo.png" alt=""></div><ul class="nav"><li><a href="index.html">首页</a></li><li><a href="ggjj.html">故宫简介</a></li><li><a href="gngd.html">馆内宫殿</a></li><li><a href="gcww.html">馆藏文物</a></li></ul><div class="tu"><img src="./images/tu.jpeg" alt=""></div></main>
</body>
</html>

五、源码获取

🥇 ~ 关注我，点赞博文~ 每天带你涨知识!
🎁1.看到这里了就[点赞+好评+收藏]三连 支持下吧，你的「点赞，好评，收藏」是我创作的动力。
💙2.想要获取本文源码，点击前往吧

相关文章：

HTML静态网页成品作业(HTML+CSS)——故宫介绍网页(4个页面)

&#x1f389;不定期分享源码&#xff0c;关注不丢失哦 文章目录 一、作品介绍二、作品演示三、代码目录四、网站代码HTML部分代码 五、源码获取 一、作品介绍 &#x1f3f7;️本套采用HTMLCSS&#xff0c;未使用Javacsript代码&#xff0c;共有4个页面。 二、作品演示 三、代…...

编程日记 2024/6/22 17:14:28

Zookeeper：客户端命令行操作

文章目录 一、help二、ls path三、create四、get path五、set六、stat七、delete八、deleteall 一、help 显示所有操作命令。 二、ls path 使用ls命令来查看当前znode的子节点[可监听] w&#xff1a;监听子节点变化。s&#xff1a;附加次级信息。 三、create 普通创建&am…...

编程日记 2024/6/22 17:13:27

区块链技术介绍和用法

区块链技术是一种分布式账本技术&#xff0c;可以记录和存储一系列交易信息&#xff0c;并通过密码学算法保证信息的安全性和不可篡改性。区块链技术的核心概念是“区块”和“链”。 每个区块包含了一部分交易信息&#xff0c;以及一个指向上一个区块的哈希值。当新的交易发生…...

编程日记 2024/6/22 17:12:26

Upload-Labs-Linux1 使用 一句话木马

解题步骤&#xff1a; 1.新建一个php文件&#xff0c;编写内容&#xff1a; <?php eval($_REQUEST[123]) ?> 2.将编写好的php文件上传&#xff0c;但是发现被阻止&#xff0c;网站只能上传图片文件。 3.解决方法&#xff1a; 将php文件改为图片文件&#xff08;例…...

编程日记 2024/6/22 17:11:24

从 Hadoop 迁移，无需淘汰和替换

我们仍然惊讶于有如此多的客户来找我们&#xff0c;希望从HDFS迁移到现代对象存储&#xff0c;如MinIO。我们现在以为每个人都已经完成了过渡&#xff0c;但每周&#xff0c;我们都会与一个决定进行过渡的主要、高技术性组织交谈。 很多时候&#xff0c;在这些讨论中&#xff…...

编程日记 2024/6/22 17:08:20

深度学习：从理论到应用的全面解析

引言 深度学习作为人工智能&#xff08;AI&#xff09;的核心技术之一&#xff0c;在过去的十年中取得了显著的进展&#xff0c;并在许多领域中展示了其强大的应用潜力。本文将从理论基础出发&#xff0c;探讨深度学习的最新进展及其在各领域的应用&#xff0c;旨在为读者提供全…...

编程日记 2024/6/22 17:07:19

【02】区块链技术应用

区块链在金融、能源、医疗、贸易、支付结算、证券等众多领域有着广泛的应用&#xff0c;但是金融依旧是区块链最大且最为重要的应用领域。 1. 区块链技术在金融领域的应用 1.2 概况 自2019年以来&#xff0c;国家互联网信息办公室已发布八批境内区块链信息服务案例清单&#…...

编程日记 2024/6/22 17:05:16

一篇文章搞懂残差网络算法

残差网络（Residual Network，简称ResNet）是一种深度学习架构，它在2015年由微软研究院的Kaiming He等四位作者提出。ResNet的提出是为了解决深度神经网络训练中的梯度消失和梯度爆炸问题，以及随着网络层数增加而出现的性能退化问题。本文将详细介绍残差网络算法的定义、产生…...

编程日记 2024/6/22 17:03:13

网络安全：Web 安全 面试题.（SQL注入）

网络安全&#xff1a;Web 安全 面试题.&#xff08;SQL注入&#xff09; 网络安全面试是指在招聘过程中,面试官会针对应聘者的网络安全相关知识和技能进行评估和考察。这种面试通常包括以下几个方面&#xff1a; &#xff08;1&#xff09;基础知识:包括网络基础知识、操作系…...

编程日记 2024/6/22 17:02:12

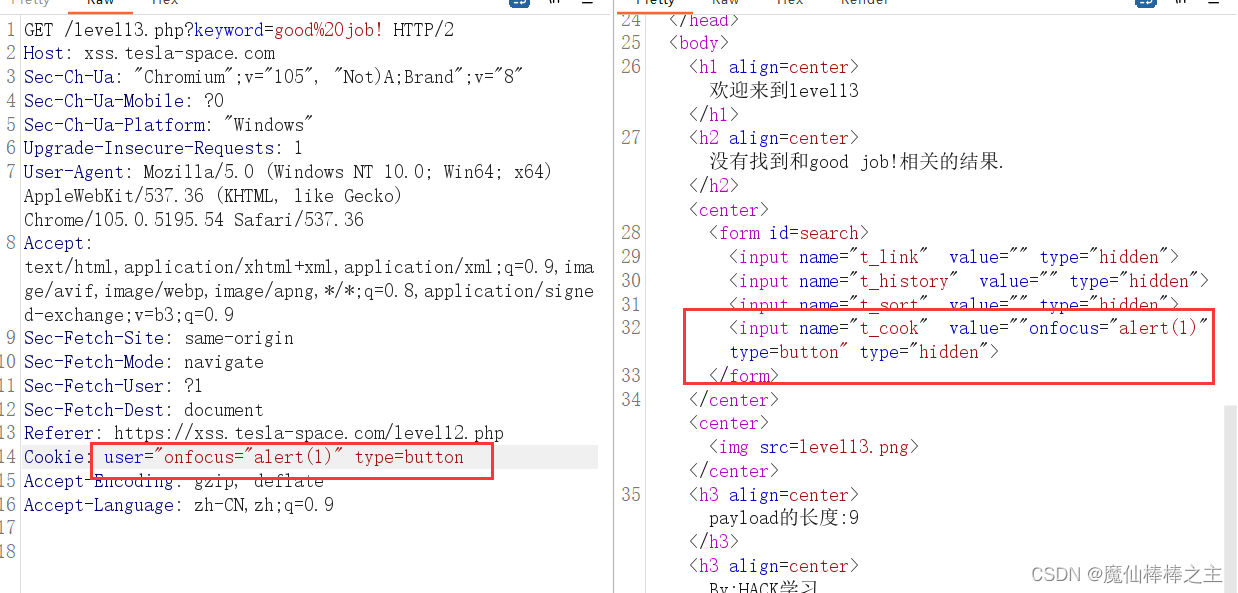
XSS学习（绕过）

学习平台&#xff1a;xss.tesla-space.com XSS学习&#xff08;绕过&#xff09; level1level2level3level4level5level6level7level8level9level10level11level12level13level14 level1 应该没有过滤 https://xss.tesla-space.com/level1.php?name<script>alert(1);&…...

编程日记 2024/6/22 17:01:11

深信服2024笔试

一 &#xff1a;服务器 小明是一名公司的IT运维工程师&#xff0c;负责管理公司的IT系统。公司总共有两个配置相同的服务器A和B&#xff0c;各运行了若干个服务。现在小明发现两台服务器上运行的服务占用的内存总和不相等(假设每个服务占用内存是-个恒定正整数)&#xff0c;打…...

编程日记 2024/6/22 16:59:09

IOS Swift 从入门到精通:闭包 第一部分

文章目录 创建基本闭包在闭包中接受参数从闭包返回值闭包作为参数尾随闭包语法 创建基本闭包 Swift 允许我们像使用字符串和整数等其他类型一样使用函数。这意味着您可以创建一个函数并将其分配给一个变量&#xff0c;使用该变量调用该函数&#xff0c;甚至可以将该函数作为参…...

编程日记 2024/6/22 16:53:03

解两道四年级奥数题（等差数列）玩玩

1、1&#xff5e;200这200个连续自然数的全部数字之和是________。 2、2&#xff0c;4&#xff0c;6&#xff0c;……&#xff0c;2008这些偶数的所有各位数字之和是________。 这两道题算易错吧&#xff0c;这里求数字之和&#xff0c;比如124这个数的全部数字之和是1247。 …...

编程日记 2024/6/22 16:52:02

深入理解Python中的并发与异步的结合使用

​ 在上一篇文章中&#xff0c;我们讨论了异步编程中的性能优化技巧&#xff0c;并简单介绍了trio和curio库。今天&#xff0c;我们将深入探讨如何将并发编程与异步编程结合使用&#xff0c;并详细讲解如何利用trio和curio库优化异步编程中的性能。 文章目录 并发与异步编程的区…...

编程日记 2024/6/22 16:47:57

如何将 ChatGPT 集成到你的应用中

在当今快速发展的技术环境中&#xff0c;将人工智能聊天解决方案集成到你的应用程序中可以显著提升用户体验和参与度。OpenAI 的 ChatGPT 以其对话能力和高级语言理解而闻名&#xff0c;对于希望在其应用程序中实现智能聊天功能的开发人员来说是一个绝佳的选择。那我们今天就来…...

编程日记 2024/6/22 16:45:55

在 Swift 中，UILabel添加点击事件的方法

在 Swift 中&#xff0c;可以使用 UITapGestureRecognizer 给 UILabel 添加点击事件。以下是一个详细的步骤和示例代码&#xff1a; 1. 创建 UILabel 并添加到视图 在 Storyboard 或代码中创建一个 UILabel 并将其添加到视图中。 2. 启用 UILabel 的用户交互 默认情况下&am…...

编程日记 2024/6/22 16:44:54

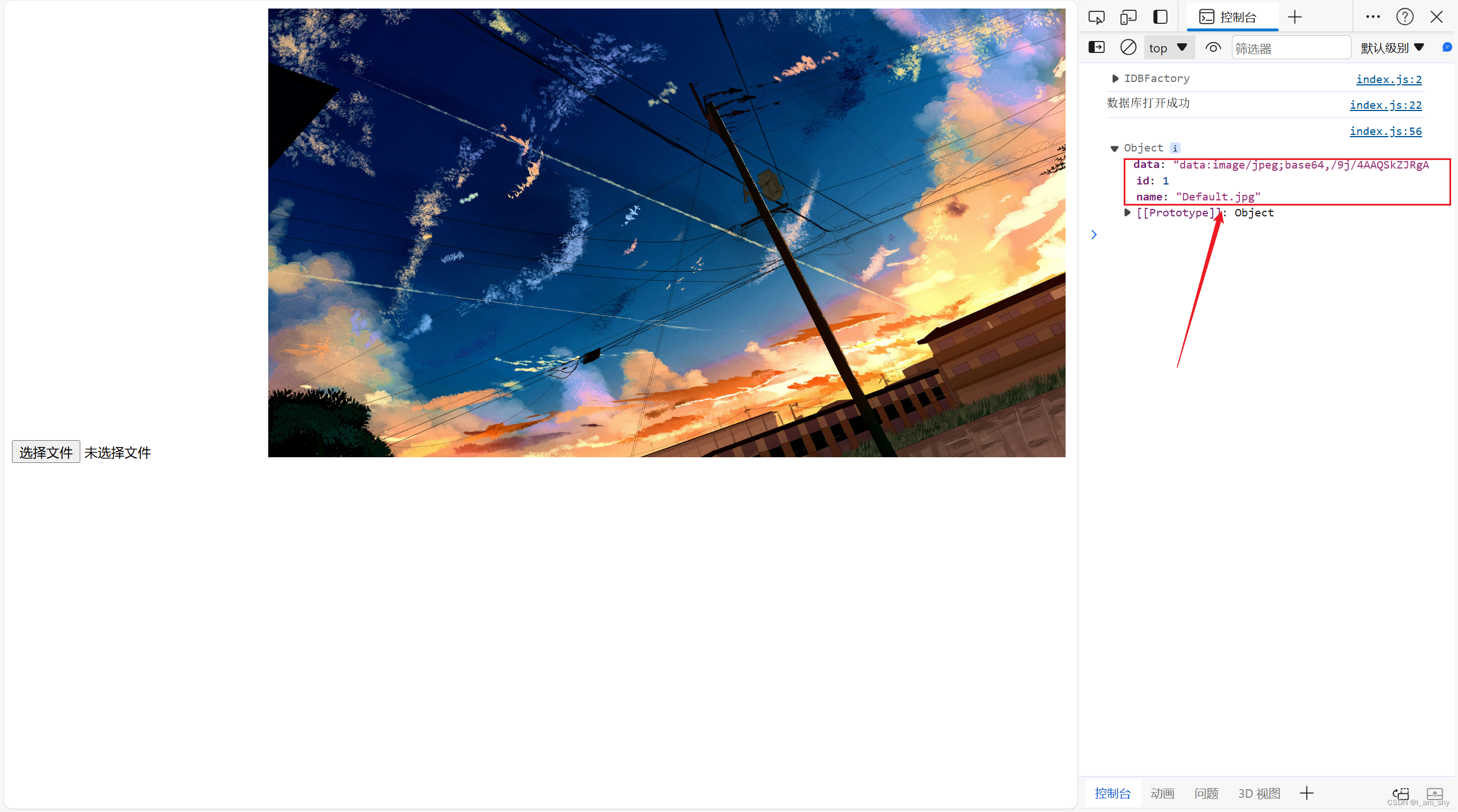
indexedDB---掌握浏览器内建数据库的基本用法

1.认识indexedDB IndexedDB 是一个浏览器内建的数据库&#xff0c;它可以存放对象格式的数据&#xff0c;类似本地存储localstore&#xff0c;但是相比localStore 10MB的存储量&#xff0c;indexedDB可存储的数据量远超过这个数值&#xff0c;具体是多少呢&#xff1f; 默认情…...

编程日记 2024/6/22 16:43:53

【css】如何修改input选中历史选项后，自动填充的蓝色背景色

自动填充前&#xff1a; 自动填充后&#xff1a; 解决办法 方法一&#xff1a;设置背景透明&#xff08;通过拉长过渡时间&#xff0c;和延迟过渡开始时间&#xff0c;掩盖input自动填充背景颜色&#xff09; PS&#xff1a;注意&#xff0c;这个过渡效果会在你的delay tim…...

编程日记 2024/6/22 16:42:52

红队内网攻防渗透：内网渗透之内网对抗：网络通讯篇防火墙组策略入站和出站规则单层双层C2正反向上线解决方案

红队内网攻防渗透 1. 内网网络通讯1.1 防火墙策略-入站规则&出站规则&自定义1.1.1 防火墙默认入站&出站策略1.1.2 防火墙自定义入站&出站策略1.1.3 内网域防火墙同步策略1.2 防火墙限制1.2.1 防火墙限制端口1.2.2 防火墙限制协议1.2.2.1 防火墙协议入站限制1.2…...

编程日记 2024/6/22 16:41:51

linux 查看进程启动方式

目录 如果是systemd管理的服务怎么快速找到对应的服务器呢 什么是CGroup 查找进程对应的systemd服务 方法一&#xff1a;查看 /proc//cgroup 文件 方法二&#xff1a;使用 ps 命令结合 --cgroup 选项 方法三&#xff1a;systemd-cgls 关于 system.slice 与 user.slice …...

编程日记 2024/6/22 16:40:50

地震勘探——干扰波识别、井中地震时距曲线特点

目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波&#xff1a;可以用来解决所提出的地质任务的波&#xff1b;干扰波&#xff1a;所有妨碍辨认、追踪有效波的其他波。 地震勘探中&#xff0c;有效波和干扰波是相对的。例如&#xff0c;在反射波…...

编程新知 2026/2/8 20:43:05

2024年赣州旅游投资集团社会招聘笔试真

2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案，答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年，()预言了电磁波的存在，并指出…...

编程新知 2025/12/10 4:08:53

新能源汽车智慧充电桩管理方案：新能源充电桩散热问题及消防安全监管方案

随着新能源汽车的快速普及&#xff0c;充电桩作为核心配套设施&#xff0c;其安全性与可靠性备受关注。然而&#xff0c;在高温、高负荷运行环境下&#xff0c;充电桩的散热问题与消防安全隐患日益凸显&#xff0c;成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

编程新知 2026/1/29 3:00:56

Spring Boot面试题精选汇总

&#x1f91f;致敬读者 &#x1f7e9;感谢阅读&#x1f7e6;笑口常开&#x1f7ea;生日快乐⬛早点睡觉 &#x1f4d8;博主相关 &#x1f7e7;博主信息&#x1f7e8;博客首页&#x1f7eb;专栏推荐&#x1f7e5;活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

编程新知 2025/9/24 23:08:17

HTML前端开发：JavaScript 常用事件详解

作为前端开发的核心&#xff0c;JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例&#xff1a; 1. onclick - 点击事件 当元素被单击时触发&#xff08;左键点击&#xff09; button.onclick function() {alert("按钮被点击了&#xff01;&…...

编程新知 2025/11/10 10:45:11

免费PDF转图片工具

免费PDF转图片工具 一款简单易用的PDF转图片工具&#xff0c;可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件&#xff0c;也不需要在线上传文件&#xff0c;保护您的隐私。 工具截图 主要特点 &#x1f680; 快速转换&#xff1a;本地转换&#xff0c;无需等待上…...

编程新知 2026/1/26 9:07:56

MySQL 部分重点知识篇

一、数据库对象 1. 主键 定义 &#xff1a;主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 &#xff1a;确保数据的完整性&#xff0c;便于数据的查询和管理。 示例 &#xff1a;在学生信息表中&#xff0c;学号可以作为主键&#xff…...

编程新知 2025/8/19 22:24:50

day36-多路IO复用

一、基本概念 &#xff08;服务器多客户端模型&#xff09; 定义&#xff1a;单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用&#xff1a;应用程序通常需要处理来自多条事件流中的事件&#xff0c;比如我现在用的电脑&#xff0c;需要同时处理键盘鼠标…...

编程新知 2026/1/31 7:42:50

python爬虫——气象数据爬取

一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用&#xff1a; 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests&#xff1a;发送 …...

编程新知 2025/12/16 7:53:39

关于easyexcel动态下拉选问题处理

前些日子突然碰到一个问题&#xff0c;说是客户的导入文件模版想支持部分导入内容的下拉选&#xff0c;于是我就找了easyexcel官网寻找解决方案&#xff0c;并没有找到合适的方案&#xff0c;没办法只能自己动手并分享出来&#xff0c;针对Java生成Excel下拉菜单时因选项过多导…...

编程新知 2026/2/6 11:08:25