C++ std::forward()
在线调试网站:
https://wandbox.org/
#include <iostream>
#include <thread>
#include <mutex> void func(int &&args) {std::cout << args << std::endl;
}int main () {int a = 10;func(20); func(a); func(std::move(a)); return 0;
}编译错误信息:需要的是右值,但是传入的是左值,类型不匹配;
prog.cc: In function 'int main()':
prog.cc:13:10: error: cannot bind rvalue reference of type 'int&&' to lvalue of type 'int'13 | func(a);| ^
prog.cc:5:17: note: initializing argument 1 of 'void func(int&&)'5 | void func(int &&args) {| ~~~~~~^~~~#include <iostream>
#include <thread>
#include <mutex> void func(int &arg) {std::cout << "func lvalue:" << arg << std::endl;
}
void func(int &&arg) {std::cout << "func rvalue" << arg << std::endl;
}template <typename T>
void wrapper(T &&args) {func(args);
}
int main() {int a = 10; wrapper(a);wrapper(20);return 0;
}最终都调用了func(int &arg)
func lvalue:10
func lvalue:20虽然咱们调用wrapper()函数时,传入的参数一个是左值,一个是右值,可是最终的输出确都是左值。缘由是咱们在中间加了一层转发函数wrapper()。
引用叠加,引用是能够叠加的,对于 T &&a; 叠加规则以下:
(1)当T类型为 Type 时,a 为 Type &&a,右值引用。
(2)当T类型为 Type& 时,a为 Type &a,左值引用。(这点还在思考中)
(3)当T类型为 Type&& 时,a为 Type &&a,右值引用。
经过引用叠加,分析以上示例可知,调用wrapper()时,wrapper(a) 是调用的原型是 wrapper(int &),是左值调用;wrapper(20)调用的原型是wrapper(int &&),是右值调用。可是在wrapper()函数内部,不管如何,args都是一个左值,在调用func()函数的时候,调用的func()原型老是func(int &)。
所以,右值引用属性不能被转发。因此,C++11提供了std::forward()函数用于完美转发。即,在转发过程当中,左值引用在被转发以后仍然保持左值属性,右值引用在被转发以后依然保持右值属性。
#include <iostream>
#include <thread>
#include <mutex> void func(int &arg) {std::cout << "func lvalue:" << arg << std::endl;
}
void func(int &&arg) {std::cout << "func rvalue:" << arg << std::endl;
}template <typename T>
void wrapper(T &&args) {//func(args);func(std::forward<T>(args));
}
int main() {int a = 10; wrapper(a);wrapper(20);return 0;
}func lvalue:10
func rvalue:20思考:
1 完美转发解决了什么问题;
2 经典应用场景是什么;(锁,线程等需要move语义的场景)
相关文章:
)
C++ std::forward()
在线调试网站: https://wandbox.org/ #include <iostream> #include <thread> #include <mutex> void func(int &&args) {std::cout << args << std::endl; }int main () {int a 10;func(20); …...
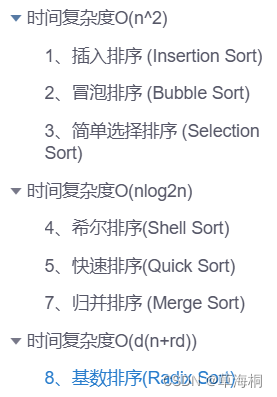
常见的8种排序(含代码):插入排序、冒泡排序、希尔排序、快速排序、简单选择排序、归并排序、堆排序、基数排序
时间复杂度O(n^2) 1、插入排序 (Insertion Sort) 从第一个元素开始,该元素可以认为已经被排序;取出下一个元素,在已经排序的元素序列中从后向前扫描;如果该元素(已排序)大于新元素,将该元素移到…...

go语言day2
使用cmd 中的 go install ; go build 命令出现 go cannot find main module 错误怎么解决? go学习-问题记录(开发环境)go: cannot find main module; see ‘go help modules‘_go: no flags specified (see go help mod edit)-CSDN博客 在本…...
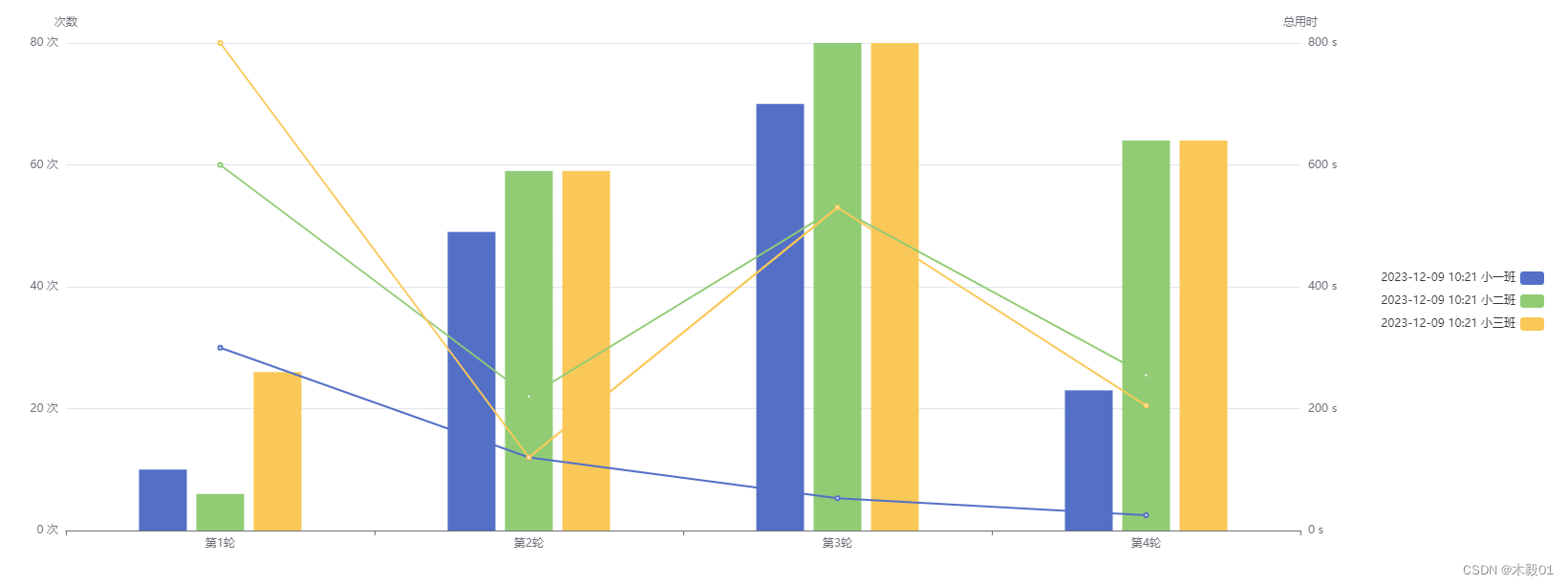
vue echarts画多柱状图+多折线图
<!--多柱状图折线图--> <div class"echarts-box" id"multiBarPlusLine"></div>import * as echarts from echarts;mounted() {this.getMultiBarPlusLine() },getMultiBarPlusLine() {const container document.getElementById(multiBar…...

cesium for unity 打包webgl失败,提示不支持
platform webgl is not supported with HDRP use the Vulkan graphics AR instead....

python开发基础——day7 序列类型方法
一、初识序列类型方法 序列类型的概念:数据的集合,在序列类型里面可以存放任意的数据,也可以对数据进行更方便的操作,这个操作是叫增删改查(crud) ( 增加(Creat),读取查询(Retrieve),更新(Update)…...

用java写一个二叉树翻转
class TreeNode {int val;TreeNode left, right;TreeNode(int val) {this.val val;left right null;} }public class BinaryTree {TreeNode root;// 递归翻转二叉树public TreeNode invertTree(TreeNode root) {if (root null) {return null;}// 递归翻转左子树和右子树Tre…...

数学建模系列(3/4):典型建模方法
目录 引言 1. 回归分析 1.1 线性回归 基本概念 Matlab实现 1.2 多元回归 基本概念 Matlab实现 1.3 非线性回归 基本概念 Matlab实现 2. 时间序列分析 2.1 时间序列的基本概念 2.2 移动平均 基本概念 Matlab实现 2.3 指数平滑 基本概念 Matlab实现 2.4 ARIM…...

AI播客下载:Machine Learning Street Talk(AI机器学习)
该频道由 Tim Scarfe 博士、Yannic Kilcher 博士和 Keith Duggar 博士管理。 他们做了出色的工作,对每个节目进行了彻底的研究,并与机器学习行业中一些受过最高教育、最全面的嘉宾进行了双向对话。 每一集都会教授一些新内容,并且提供未经过滤…...
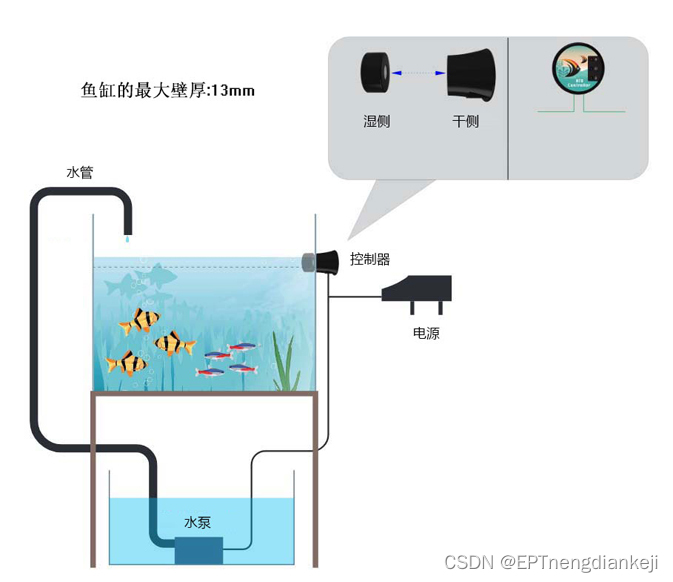
鱼缸补水器工作原理是什么
鱼缸补水器是一种应用广泛的智能设备,主要用于自动监测和补充鱼缸内的水位,以确保鱼类生存环境的稳定。其工作原理简单而高效,为饲主提供了方便和安全的使用体验。 该补水器通常由两部分组成:控制器和吸盘。首先,用户…...

Linux-Tomcat服务配置到系统服务
目录 前言一、系统环境二、配置步骤step1 了解环境的安装路径step2 配置生成tomcat.pid文件step3 配置tomcat.service文件 三、测试systemctl命令管理Tomcat服务3.1 systemctl命令启动Tomcat服务3.2 systemctl命令查看Tomcat服务3.3 systemctl命令关闭Tomcat服务3.4 systemctl命…...

Python抓取高考网图片
Python抓取高考网图片 一、项目介绍二、完整代码一、项目介绍 本次采集的目标是高考网(http://www.gaokao.com/gkpic/)的图片,实现图片自动下载。高考网主页如下图: 爬取的流程包括寻找数据接口,发送请求,解析图片链接,向图片链接发送请求获取数据,最后保存数据。 二…...

Vue配置项data
data 目录 data 目录类型介绍关键原理编译过程 Vue2Vue3 📌Vue.js 中的 data(Obj/Function)属性是 Vue 实例的一个配置选项 类型介绍 对象式 对于根实例或者非复用组件,通常直接提供一个对象字面量作为 data 的值。在对象式中…...
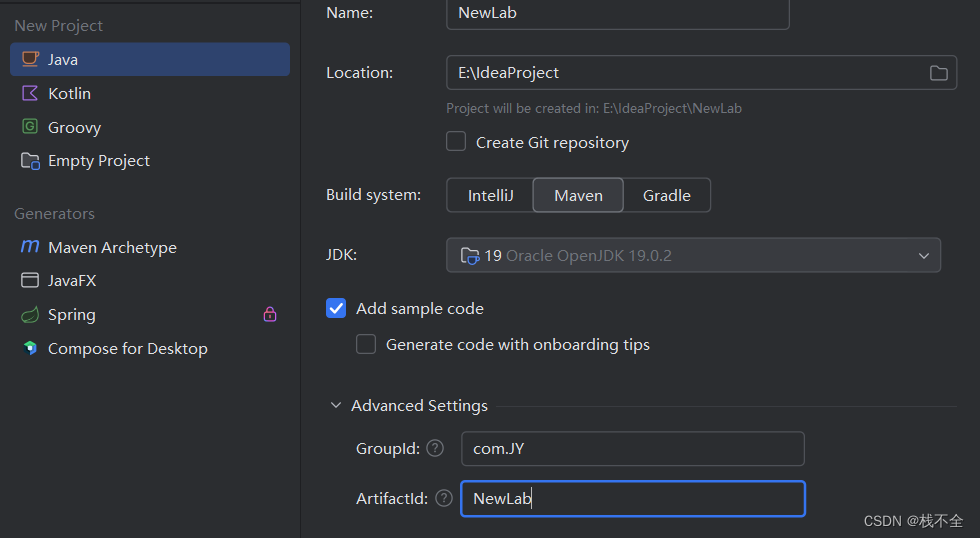
在IDEA 2024.1.3 (Community Edition)中创建Maven项目
本篇博客承继自博客:Windows系统Maven下载安装-CSDN博客 Maven版本:maven-3.9.5 修改设置: 首先先对Idea的Maven依赖进行设置;打开Idea,选择“Costomize”,选择最下边的"All settings" 之后找…...

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-28批量规范化
28批量规范化 """可持续加速深层网络的收敛速度""" import torch from torch import nn import liliPytorch as lp import matplotlib.pyplot as pltdef batch_norm(X, gamma, beta, moving_mean, moving_var, eps, momentum):""&quo…...
Apache Paimon系列之:Append Table和Append Queue
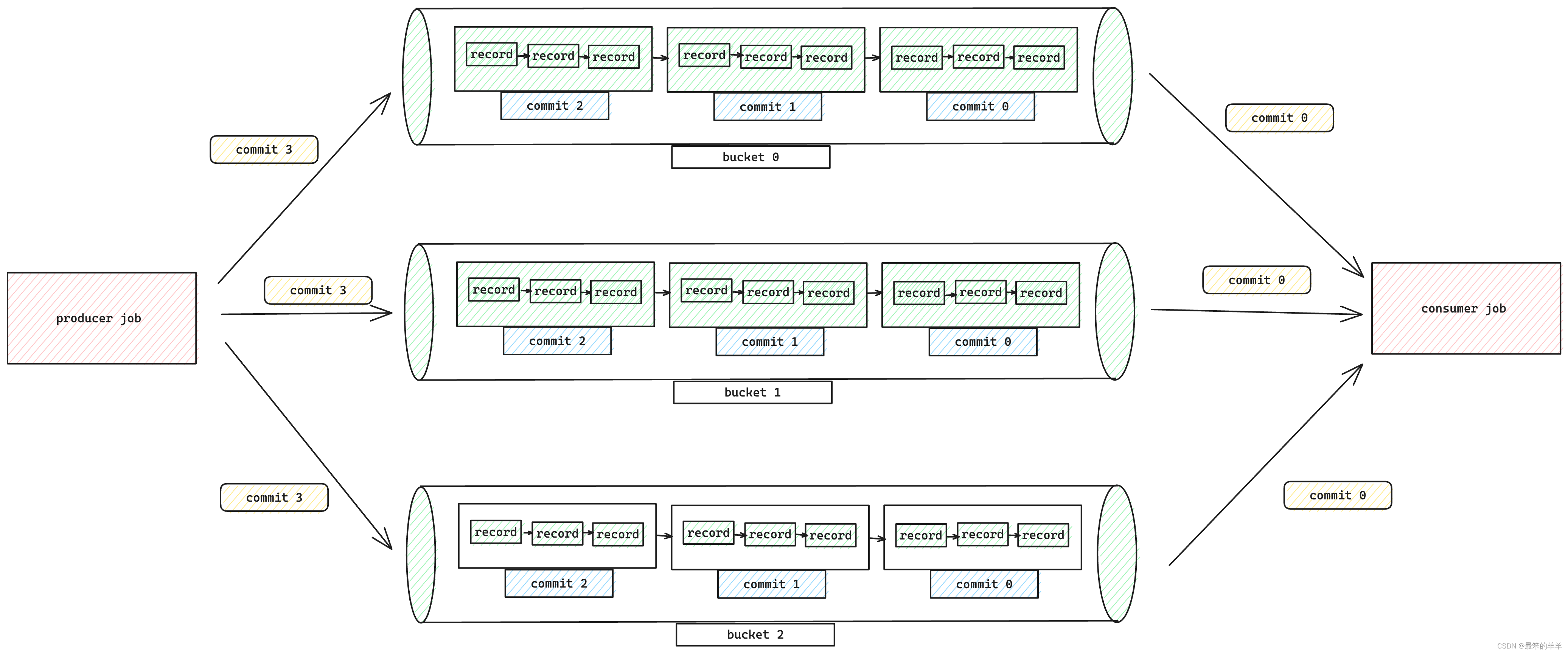
Apache Paimon系列之:Append Table和Append Queue 一、Append Table二、Data Distribution三、自动小文件合并四、Append Queue五、压缩六、Streaming Source七、Watermark Definition八、Bounded Stream 一、Append Table 如果表没有定义主键,则默认为…...

Vue使用vue-esign实现在线签名 加入水印
Vue在线签名 一、目的二、样式三、代码1、依赖2、代码2.1 在线签名组件2.1.1 基础的2.1.2 携带时间水印的 2.2父组件 一、目的 又来了一个问题,直接让我在线签名(还不能存储base64),并且还得上传,我直接***违禁词。 好…...

与码无关:分数限制下,选好专业还是选好学校?
本文的目标读者:24届的高考生和家长。 写这篇非技术性文章,是因为我看到了24届考生和21年的我同样迷茫。 事先声明,本文带有强烈的个人思考色彩,可能会引起不适,如有不同观点,欢迎在评论区讨论。 一、前言…...

什么是负载均衡技术?
随着网络技术的快速发展,互联网行业也越来越广泛,人们的日常生活中也离不开网络技术,大量的用户进行浏览访问网站时,企业会使用负载均衡技术,降低当前网站的负载,以此来提高网站的访问速度。 今天小编就来给…...

存在重复元素Ⅱ python3
存在重复元素Ⅱ 问题描述解题思路代码实现复杂度 问题描述 给你一个整数数组 nums 和一个整数 k ,判断数组中是否存在两个 不同的索引 i 和 j ,满足 nums[i] nums[j] 且 abs(i - j) < k 。如果存在,返回 true ;否则ÿ…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...
中关于正整数输入的校验规则)
Element Plus 表单(el-form)中关于正整数输入的校验规则
目录 1 单个正整数输入1.1 模板1.2 校验规则 2 两个正整数输入(联动)2.1 模板2.2 校验规则2.3 CSS 1 单个正整数输入 1.1 模板 <el-formref"formRef":model"formData":rules"formRules"label-width"150px"…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

深度学习水论文:mamba+图像增强
🧀当前视觉领域对高效长序列建模需求激增,对Mamba图像增强这方向的研究自然也逐渐火热。原因在于其高效长程建模,以及动态计算优势,在图像质量提升和细节恢复方面有难以替代的作用。 🧀因此短时间内,就有不…...
