AtCoder Beginner Contest 216(F)
F - Max Sum Counting
链接: F - Max Sum Counting
题意
两个 大小为 nnn 的序列 aiaiai 和 bibibi,任意选取一些下标 iii,求 max(ai)>=∑bi\max(ai) >= \sum{bi}max(ai)>=∑bi的方案数。
解析
首先考虑状态 一是和, 二是最大值, 但这样我们发现需要三重循环,在 n=5000n = 5000n=5000 的情况下是不能接受的复杂度,于是我们想到按 aiaiai 排序后,我们只计算 ∑bi\sum{bi}∑bi 的方案,将所有满足条件的方案再计入答案,就变成一个普通的背包求方案数了。
对于要按 aiaiai 排序的证明:
因为我们没有多开一维来记录 max(ai)\max(ai)max(ai) 最大值, 所以对于每一种 bibibi 和为 sumsumsum 他的状态集合可能有许多不同的 max(ai)max(ai)max(ai)。
假设和为 sumsumsum 有 max(ai)=ajmax(ai) = ajmax(ai)=aj,maxai=akmax{ai} = akmaxai=ak 两种可能,若是不按 aiaiai 排序 会导致不知道 aj,akaj, akaj,ak 那种状态可以转移。
假设 sum=10sum = 10sum=10, aj=100aj = 100aj=100 ,ak=10ak = 10ak=10 当前的 ai=10ai = 10ai=10 ,bi=10bi = 10bi=10 那么只能从 ajajaj 转移 因为只有这种才保证 max(ai)>∑bi\max(ai) > \sum{bi}max(ai)>∑bi 但已经把 aj,akaj, akaj,ak 的状态整合在一起了不能分开。
若是按 aiaiai 排序,新来的 aiaiai 一定是目前的最大值, 一定比 ajajaj 和 akakak 都大 于是一个状态包含的所有情况都能转移。
代码
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5010, mod = 998244353, MAX = 5000;
struct node{int ai, bi;bool operator < (const node &A)const{return ai < A.ai;}
}s[N];
int f[N];//bi之和价值为i的方案数
int main(){int n;cin >> n;for(int i = 1; i <= n; i ++) cin >> s[i].ai;for(int i = 1; i <= n; i ++) cin >> s[i].bi;sort(s + 1, s + 1 + n);f[0] = 1;int ans = 0;for(int i = 1; i <= n; i ++){for(int j = MAX; j >= s[i].bi; j --){f[j] = (f[j] + f[j - s[i].bi]) % mod;if(j <= s[i].ai) ans = (ans + f[j - s[i].bi]) % mod;}}cout << ans;return 0;
}
相关文章:
)
AtCoder Beginner Contest 216(F)
F - Max Sum Counting 链接: F - Max Sum Counting 题意 两个 大小为 nnn 的序列 aiaiai 和 bibibi,任意选取一些下标 iii,求 max(ai)>∑bi\max(ai) > \sum{bi}max(ai)>∑bi的方案数。 解析 首先考虑状态 一是和,…...

每天学一点之Stream流相关操作
StreamAPI 一、Stream特点 Stream是数据渠道,用于操作数据源(集合、数组等)所生成的元素序列。“集合讲的是数据,负责存储数据,Stream流讲的是计算,负责处理数据!” 注意: ①Str…...

MatCap模拟光照效果实现
大家好,我是阿赵 之前介绍过各种光照模型的实现方法。那些光照模型的实现虽然有算法上的不同,但基本上都是灯光方向和法线方向的计算得出的明暗结果。 下面介绍一种叫做MatCap的模拟光照效果,这种方式计算非常简单,脱离灯光的计算…...

二十一、PG管理
一、 PG异常状态说明 1、 PG状态介绍 可以通过ceph pg stat命令查看PG当前状态,健康状态为“active clean” [rootrbd01 ~]# ceph pg stat 192 pgs: 192 activeclean; 1.3 KiB data, 64 MiB used, 114 GiB / 120 GiB avail; 85 B/s rd, 0 op/s2、pg常见状态 状…...

SAPUI5开发01_01-Installing Eclipse
1.0 简要要求概述: 本节您将安装SAPUI 5,以及如何在Eclipse Juno中集成SAPUI 5工具。 1.1 安装JDK JDK 是一种用于构建在 Java 平台上发布的应用程序、Applet 和组件的开发环境,即编写 Java 程序必须使用 JDK,它提供了编译和运行 Java 程序的环境。 在安装 JDK 之前,首…...
Qt之高仿QQ系统设置界面
QQ或360安全卫士的设置界面都是非常有特点的,所有的配置项都在一个垂直的ScrollArea中,但是又能通过左侧的导航栏点击定位。这样做的好处是既方便查看指定配置项,又方便查看所有配置项。 一.效果 下面左边是当前最新版QQ的系统设置界面,右边是我的高仿版本,几乎一毛一样…...

JVM概览:内存空间与数据存储
核心的五个部分虚拟机栈:局部变量中基础类型数据、对象的引用存储的位置,线程独立的。堆:大量运行时对象都在这个区域存储,线程共享的。方法区:存储运行时代码、类变量、常量池、构造器等信息,线程共享。程…...
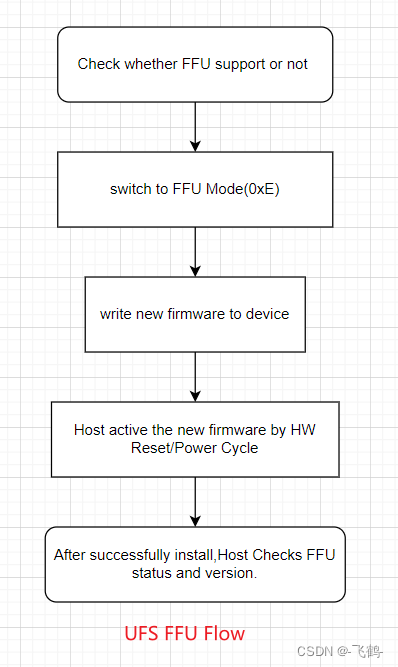
固态存储设备固件升级方案
1. 前言 随着数字化时代的发展,数字数据的量越来越大,相应的数据存储的需求也越来越大,存储设备产业也是蓬勃发展。存储设备产业中,发展最为迅猛的则是固态存储(Solid State Storage,SSS)。数字化时代,海量…...
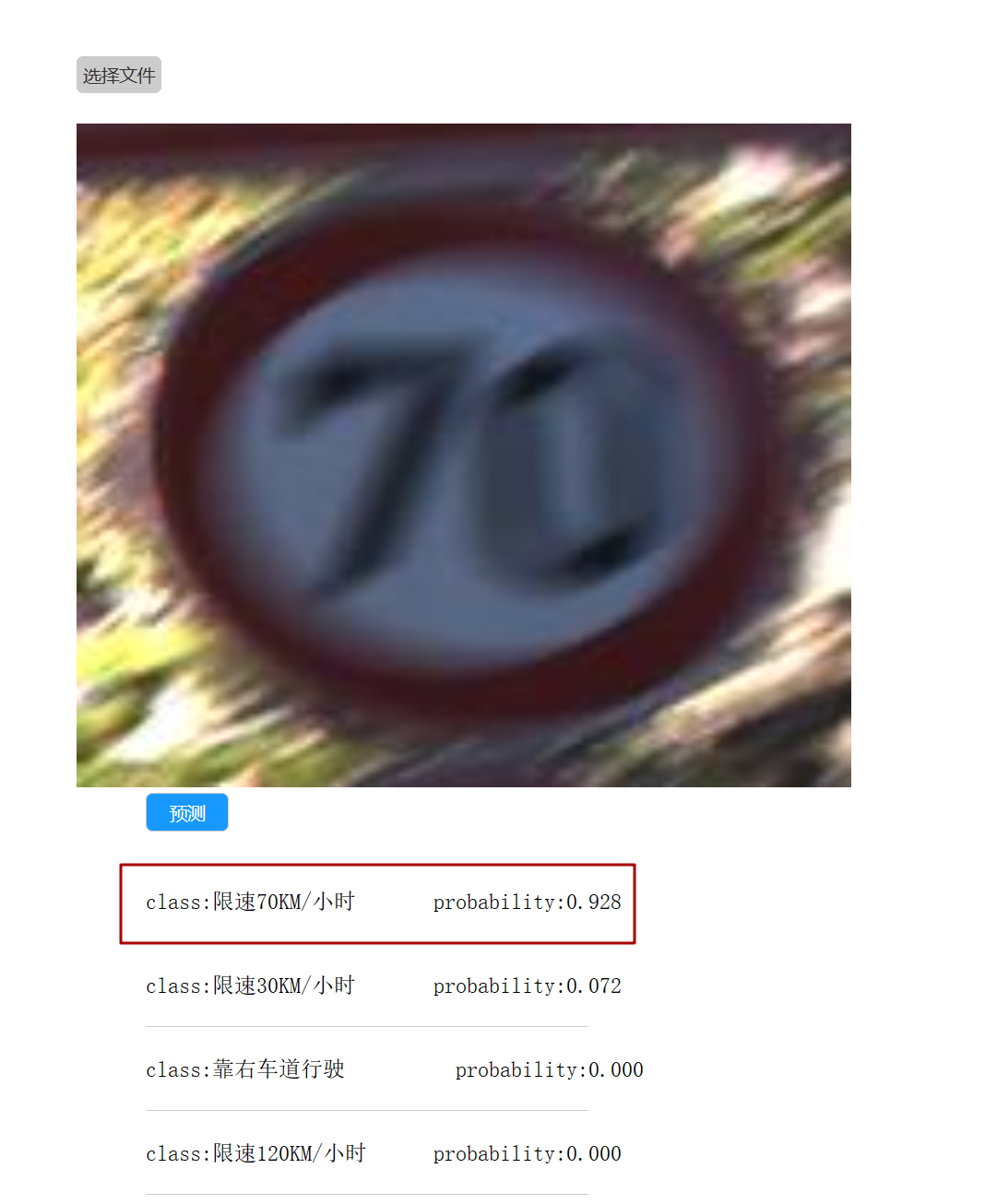
Python交通标志识别基于卷积神经网络的保姆级教程(Tensorflow)
项目介绍 TensorFlow2.X 搭建卷积神经网络(CNN),实现交通标志识别。搭建的卷积神经网络是类似VGG的结构(卷积层与池化层反复堆叠,然后经过全连接层,最后用softmax映射为每个类别的概率,概率最大的即为识别…...

基于Selenium+Python的web自动化测试框架(附框架源码+项目实战)
目录 一、什么是Selenium? 二、自动化测试框架 三、自动化框架的设计和实现 四、需要改进的模块 五、总结 总结感谢每一个认真阅读我文章的人!!! 重点:配套学习资料和视频教学 一、什么是Selenium? …...

Python进阶-----高阶函数zip() 函数
目录 前言: zip() 函数简介 运作过程: 应用实例 1.有序序列结合 2.无序序列结合 3.长度不统一的情况 前言: 家人们,看到标题应该都不陌生了吧,我们都知道压缩包文件的后缀就是zip的,当然还有r…...

win10打印机拒绝访问解决方法
一直以来,在安装使用共享打印机打印一些文件的时候,会遇到错误提示:“无法访问.你可能没有权限使用网络资源。请与这台服务器的管理员联系”的问题,那为什么共享打印机拒绝访问呢?别着急,下面为大家带来相关的解决方法…...

深度学习训练营之数据增强
深度学习训练营学习内容原文链接环境介绍前置工作设置GPU加载数据创建测试集数据类型查看以及数据归一化数据增强操作使用嵌入model的方法进行数据增强模型训练结果可视化自定义数据增强查看数据增强后的图片学习内容 在深度学习当中,由于准备数据集本身是一件十分复杂的过程,…...
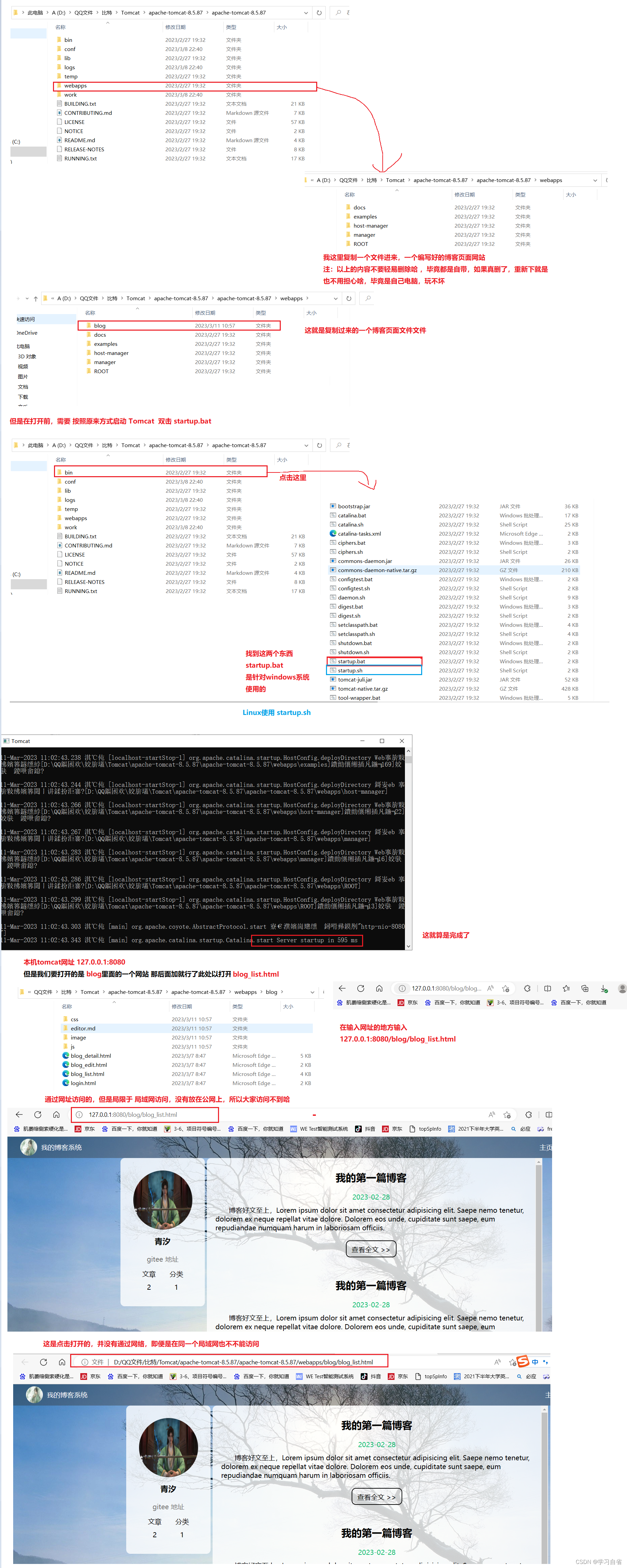
Tomcat安装及启动
日升时奋斗,日落时自省 目录 1、Tomcat下载 2、JDK安装及配置环境 3、Tomcat配置环境 4、启动Tomcat 5、部署演示 1、Tomcat下载 直接入主题,下载Tomcat 首先就是别下错了,直接找官方如何看是不是广告,或者造假 搜索Tomc…...

【专项训练】排序算法
排序算法 非比较类的排序,基本上就是放在一个数组里面,统计每个数出现的次序 最重要的排序是比较类排序! O(nlogn)的3个排序,必须要会!即:堆排序、快速排序、归并排序! 快速排序:分治 经典快排 def quickSort1(arr...

Android压测测试事件行为参数对照表
执行参数参数说明颗粒度指标基础参数--throttle <ms> 用于指定用户操作间的时延。 -s 随机数种子,用于指定伪随机数生成器的seed值,如果seed值相同,则产生的时间序列也相同。多用于重测、复现问题。 -v 指定输出日志的级别,…...

【观察】亚信科技:“飞轮效应”背后的数智化创新“延长线”
著名管理学家吉姆柯林斯在《从优秀到卓越》一书中提出“飞轮效应”,它指的是为了使静止的飞轮转动起来,一开始必须使很大的力气,每转一圈都很费力,但达到某一临界点后,飞轮的重力和冲力就会成为推动力的一部分…...

QT编程从入门到精通之十四:“第五章:Qt GUI应用程序设计”之“5.1 UI文件设计与运行机制”之“5.1.1 项目文件组成”
目录 第五章:Qt GUI应用程序设计 5.1 UI文件设计与运行机制 5.1.1 项目文件组成 第五章:Qt GUI应用程序设计...
730. 机器人跳跃问题)
(二分)730. 机器人跳跃问题
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 AcWing 730. 机器人跳跃问题 - AcWing 一些话 // 向上取整 mid的表示要写成l r 1 >> 1即可,向下取整 mid l r >> 1 // 这里我用了浮点二分,mid (l r) / 2,最…...
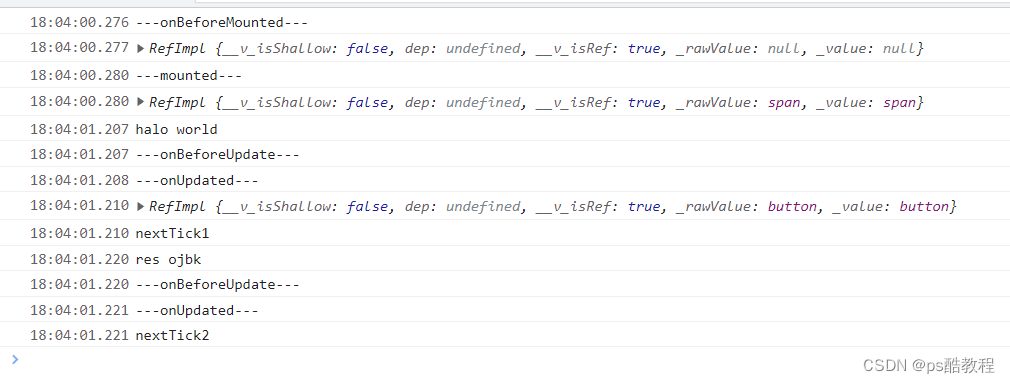
vue3使用nextTick
发现nextTick必须放在修改一个响应式数据之后,才会在onUpdated之后被调用,如果nextTick是放在所有对响应式数据修改之前,则nextTick里面的回调函数会在onBeforeUpdate方法执行前就被调用了。可是nextTick必须等到onUpdated执行完成之后执行&a…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...
