Python进阶-----高阶函数zip() 函数
目录
前言:
zip() 函数简介
运作过程:
应用实例
1.有序序列结合
2.无序序列结合
3.长度不统一的情况
前言:
家人们,看到标题应该都不陌生了吧,我们都知道压缩包文件的后缀就是zip的,当然还有rar等类型,在Python中也有这么一个函数叫做zip() 函数,这个函数也是有类似的压缩功能,那下面就一起来看看吧!
zip() 函数简介
进入Python中,输入help(zip) 获取信息帮助,如图所示:
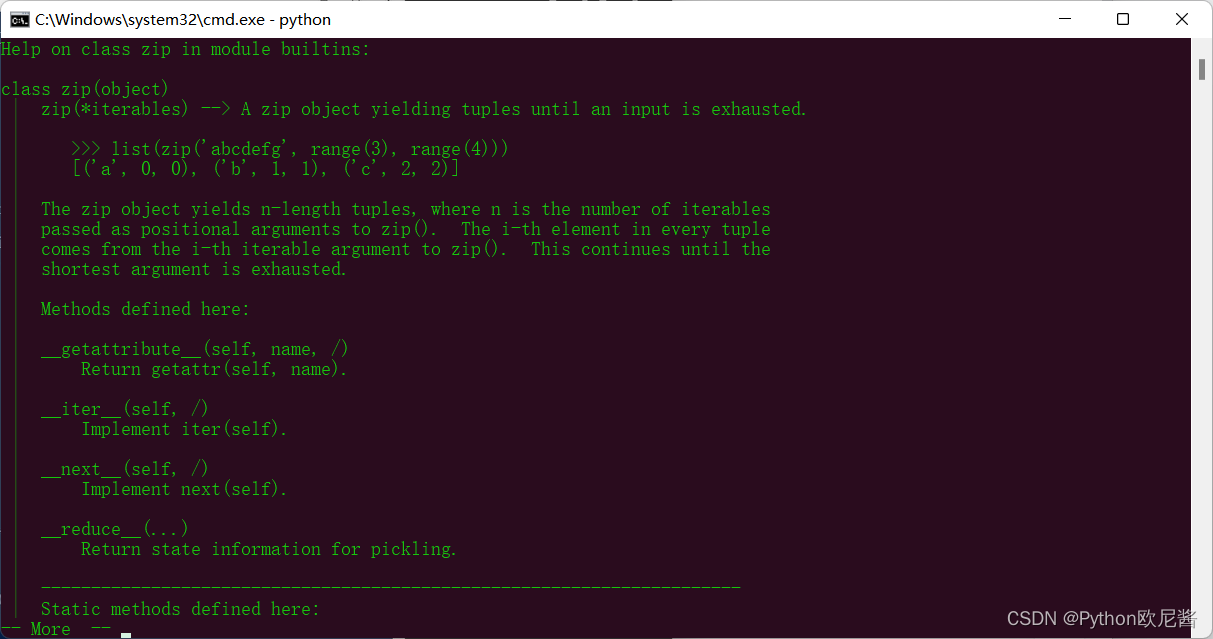
函数原型:
zip(iterable……)
说明:iterable……是表示多个可迭代对象
运作过程:
在Python中,zip() 函数可以把两个或者两个以上的可迭代对象进行聚合压缩,然后生成一个元组形式的迭代器(zip类型)并且返回,实际上就是把一些不相关的东西聚合到一起,通过另一种形式输出(这也是压缩文件的运作过程)
图解:(一般对于有序序列而已)

应用实例
1.有序序列结合
有序序列是有下标位置的,所以结果过程就是下标相同的结合为一个元组
示例1:列表与元组结合
a=[1,2,3,4,5]
b=('a','b','c','d','e')
conbine=zip(a,b) #获取到可迭代压缩对象
print(list(conbine)) #通过列表类型转换输出
#输出结果:[(1, 'a'), (2, 'b'), (3, 'c'), (4, 'd'), (5, 'e')]示例2:实现两个列表同时参与循环
a=[1,2,3,4,5]
b=['a','b','c','d','e']
conbine=zip(a,b)
for i,j in conbine: #通过循环输出可迭代对象print(i,j)
# 1 a
# 2 b
# 3 c
# 4 d
# 5 e示例3:range() 参与
conbine=zip(range(5),[chr(x) for x in range(65,70)])
print(list(conbine))
#输出结果:[(0, 'A'), (1, 'B'), (2, 'C'), (3, 'D'), (4, 'E')]示例4:多个有序序列结合
a=[i for i in range(5)]
b=['a','b','c','d','e']
c=('jack','dick','john','amy','tom')
con=zip(a,b,c)
print(list(con))
#[(0, 'a', 'jack'), (1, 'b', 'dick'), (2, 'c', 'john'), (3, 'd', 'amy'), (4, 'e', 'tom')]2.无序序列结合
示例1:集合之间的结合
a={2,1,3,4,5}
c={'a','b','c','d','e'}
con=zip(a,c)
print(list(con))
#输出结果:[(1, 'd'), (2, 'e'), (3, 'b'), (4, 'c'), (5, 'a')]集合是无序序列的,所以在结合的过程中是随机的,没有按照位置下标一一对应
示例2:构建字典
li=['jack','dick','john']
li1=[98,88,68]
di=dict(zip(li,li1))
print(di)
#输出结果:{'jack': 98, 'dick': 88, 'john': 68}3.长度不统一的情况
zip() 函数是一种按照下标位置一对一结合再一期的,当如果出现长度不一样的结合序列的时候,当其中一个序列结合完成了之后就结束(也就是木桶效应),取决于最短的那个
示例:
li=['jack','dick','john','amy']
a=tuple(x for x in range(10))
print(len(li),len(a)) #长度分别为:4 10
con=zip(li,a)
print(list(con))
#输出结果:[('jack', 0), ('dick', 1), ('john', 2), ('amy', 3)]好了,这个函数就介绍了到这里就,是不是很简单呢?学会了快去实践一下吧!!
分享一张壁纸:

相关文章:

Python进阶-----高阶函数zip() 函数
目录 前言: zip() 函数简介 运作过程: 应用实例 1.有序序列结合 2.无序序列结合 3.长度不统一的情况 前言: 家人们,看到标题应该都不陌生了吧,我们都知道压缩包文件的后缀就是zip的,当然还有r…...

win10打印机拒绝访问解决方法
一直以来,在安装使用共享打印机打印一些文件的时候,会遇到错误提示:“无法访问.你可能没有权限使用网络资源。请与这台服务器的管理员联系”的问题,那为什么共享打印机拒绝访问呢?别着急,下面为大家带来相关的解决方法…...

深度学习训练营之数据增强
深度学习训练营学习内容原文链接环境介绍前置工作设置GPU加载数据创建测试集数据类型查看以及数据归一化数据增强操作使用嵌入model的方法进行数据增强模型训练结果可视化自定义数据增强查看数据增强后的图片学习内容 在深度学习当中,由于准备数据集本身是一件十分复杂的过程,…...
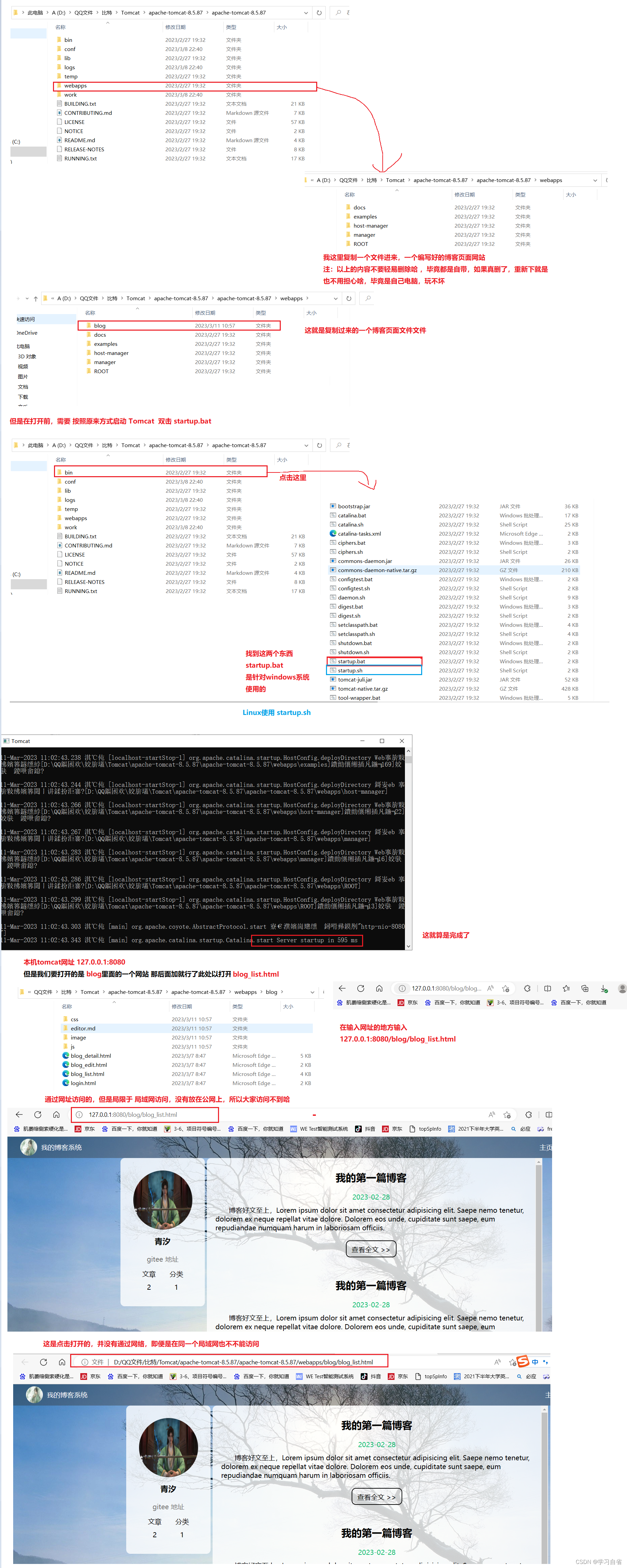
Tomcat安装及启动
日升时奋斗,日落时自省 目录 1、Tomcat下载 2、JDK安装及配置环境 3、Tomcat配置环境 4、启动Tomcat 5、部署演示 1、Tomcat下载 直接入主题,下载Tomcat 首先就是别下错了,直接找官方如何看是不是广告,或者造假 搜索Tomc…...

【专项训练】排序算法
排序算法 非比较类的排序,基本上就是放在一个数组里面,统计每个数出现的次序 最重要的排序是比较类排序! O(nlogn)的3个排序,必须要会!即:堆排序、快速排序、归并排序! 快速排序:分治 经典快排 def quickSort1(arr...

Android压测测试事件行为参数对照表
执行参数参数说明颗粒度指标基础参数--throttle <ms> 用于指定用户操作间的时延。 -s 随机数种子,用于指定伪随机数生成器的seed值,如果seed值相同,则产生的时间序列也相同。多用于重测、复现问题。 -v 指定输出日志的级别,…...

【观察】亚信科技:“飞轮效应”背后的数智化创新“延长线”
著名管理学家吉姆柯林斯在《从优秀到卓越》一书中提出“飞轮效应”,它指的是为了使静止的飞轮转动起来,一开始必须使很大的力气,每转一圈都很费力,但达到某一临界点后,飞轮的重力和冲力就会成为推动力的一部分…...

QT编程从入门到精通之十四:“第五章:Qt GUI应用程序设计”之“5.1 UI文件设计与运行机制”之“5.1.1 项目文件组成”
目录 第五章:Qt GUI应用程序设计 5.1 UI文件设计与运行机制 5.1.1 项目文件组成 第五章:Qt GUI应用程序设计...
730. 机器人跳跃问题)
(二分)730. 机器人跳跃问题
目录 题目链接 一些话 切入点 流程 套路 ac代码 题目链接 AcWing 730. 机器人跳跃问题 - AcWing 一些话 // 向上取整 mid的表示要写成l r 1 >> 1即可,向下取整 mid l r >> 1 // 这里我用了浮点二分,mid (l r) / 2,最…...
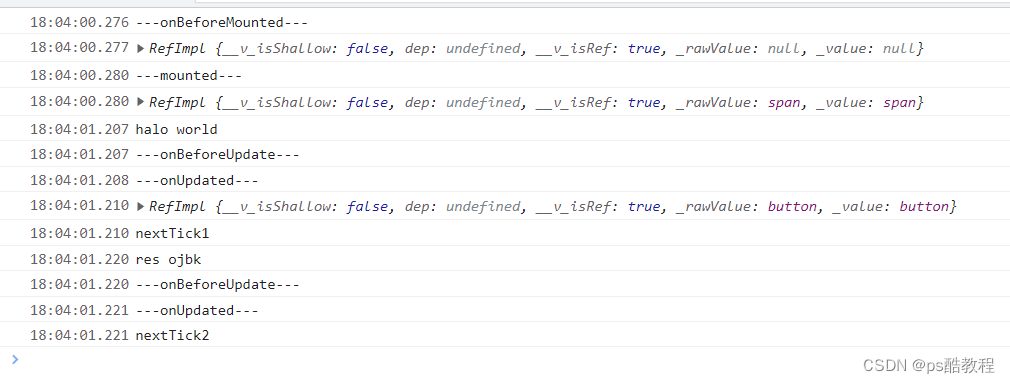
vue3使用nextTick
发现nextTick必须放在修改一个响应式数据之后,才会在onUpdated之后被调用,如果nextTick是放在所有对响应式数据修改之前,则nextTick里面的回调函数会在onBeforeUpdate方法执行前就被调用了。可是nextTick必须等到onUpdated执行完成之后执行&a…...

传统图像处理之颜色特征
博主简介 博主是一名大二学生,主攻人工智能研究。感谢让我们在CSDN相遇,博主致力于在这里分享关于人工智能,c,Python,爬虫等方面知识的分享。 如果有需要的小伙伴可以关注博主,博主会继续更新的,…...

GPS问题调试—MobileLog中有关GPS关键LOG的释义
GPS问题调试—MobileLog中有关GPS关键LOG的释义 [DESCRIPTION] 在mobile log中,有很多GPS相关的log出现在main log和kernel log、properties文件中,他们的意思是什么,通过这篇文档进行总结,以便在处理GPS 问题时,能够根据这些log快速的收敛问题。 [SOLUTION] 特别先提醒…...

【企业管理】你真的理解向下管理吗?
导读:拜读陈老师一篇文章《不会向下负责,你凭什么做管理者?》,引发不少共鸣,“很多管理者有一种错误的观念,认为管理是向下管理,向上负责。其实应该反过来,是向上管理,向…...

Centos7 硬盘挂载流程
1、添加硬盘到Linux,添加后重启系统2、查看添加的硬盘,lsblksdb 8:16020G 0disk3、分区fdisk /dev/sdbmnw其余默认,直接回车再次查看分区情况,lsblksdb1 8:17 0 20G 0 part4、格式化mkfs -t ext4 /dev/sdb15、挂载mkdir /home/new…...

认识vite_vue3 初始化项目到打包
从0到1创建vite_vue3的项目背景效果vite介绍(对比和vuecli的区别)使用npm创建vitevitevuie3创建安装antdesignvite自动按需引入(vite亮点)请求代理proxy打包背景 vue2在使用过程中对象的响应式不好用新增属性的使用$set才能实现效…...

【Go】cron时间格式
【Go】cron时间格式 Minutes:分钟,取值范围[0-59],支持特殊字符* / , -;Hours:小时,取值范围[0-23],支持特殊字符* / , -;Day of month:每月的第几天,取值范…...
leetcode 55. 跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。 数组中的每个元素代表你在该位置可以跳跃的最大长度。 判断你是否能够到达最后一个下标。 示例 1: 输入:nums [2,3,1,1,4] 输出:true 解释:可以先跳 1 …...

Linux:文件流指针 与 文件描述符
目录一、文件描述符二、文件流指针三、缓冲区之前讲解过了IO库函数和IO接口,库函数是对系统调用接口的封装,也就是说实际上在库函数内部是通过调用系统调用接口来完成最终功能的。 库函数通过文件流指针操作文件,系统调用接口通过文件描述符操…...
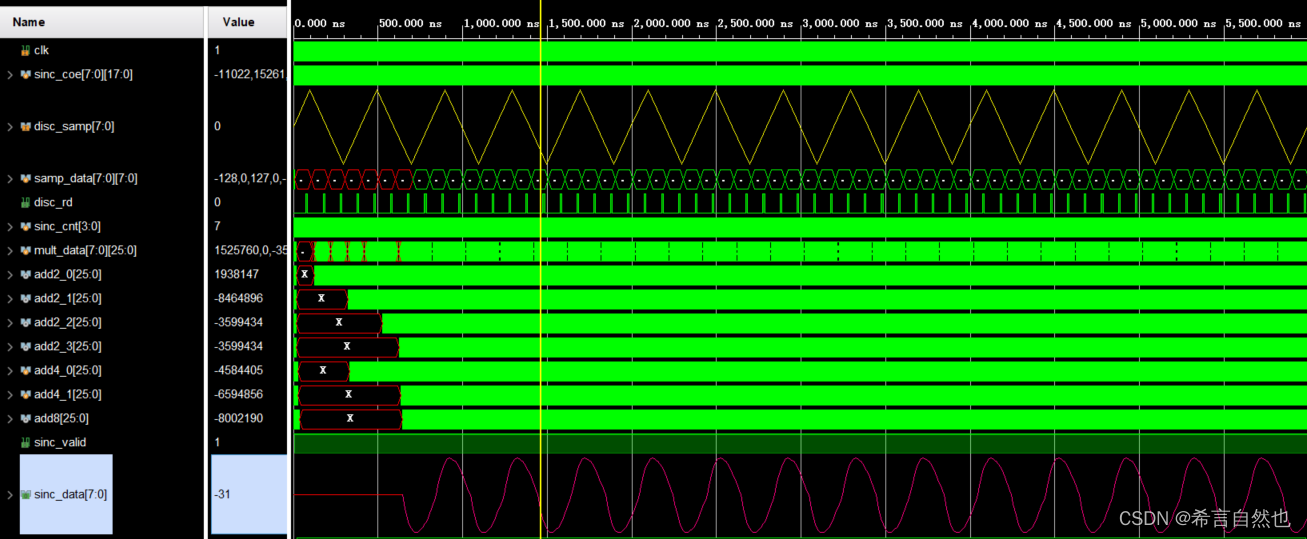
基于FPGA实现正弦插值算法
1、正弦插值的算法分析 1.1 信号在时域与频域的映射关系 在进行正弦算法分析之前,我们回顾一下《数字信号处理》课程中,对于信号在时域与频域之间的映射关系,如下图。 对于上图中的原始信号x(t),使用ADC对信号进行采样࿰…...

JavaWeb_会话技术
文章目录会话跟踪技术的概述Cookie概念Cookie工作流程Cookie基本使用发送Cookie获取CookieCookie原理分析Cookie的使用细节Cookie的存活时间Cookie存储中文SessionSession的基本使用概念工作流程Session的基本使用Session的原理分析Session的使用细节Session的钝化与活化Sessio…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

探索Selenium:自动化测试的神奇钥匙
目录 一、Selenium 是什么1.1 定义与概念1.2 发展历程1.3 功能概述 二、Selenium 工作原理剖析2.1 架构组成2.2 工作流程2.3 通信机制 三、Selenium 的优势3.1 跨浏览器与平台支持3.2 丰富的语言支持3.3 强大的社区支持 四、Selenium 的应用场景4.1 Web 应用自动化测试4.2 数据…...

协议转换利器,profinet转ethercat网关的两大派系,各有千秋
随着工业以太网的发展,其高效、便捷、协议开放、易于冗余等诸多优点,被越来越多的工业现场所采用。西门子SIMATIC S7-1200/1500系列PLC集成有Profinet接口,具有实时性、开放性,使用TCP/IP和IT标准,符合基于工业以太网的…...
