链表中环的入口节点
链表中环的入口节点
描述
链表中环的入口节点
给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。
数据范围: n≤10000, 1<=结点值<=10000
要求:空间复杂度 O(1),时间复杂度 O(n)
解法一
解法一:有环的链表,在遍历时会在环中一直循环,想要获得环的入口结点,
直观地想,可以使用hash法保存出现的结点,当重复环的遍历过程时,第一次碰到重复的结点即为环入口结点B。
解法二
解法二:通过定义slow和fast指针,slow每走一步,fast走两步,若是有环,则一定会在环的某个结点处相遇(slow == fast),
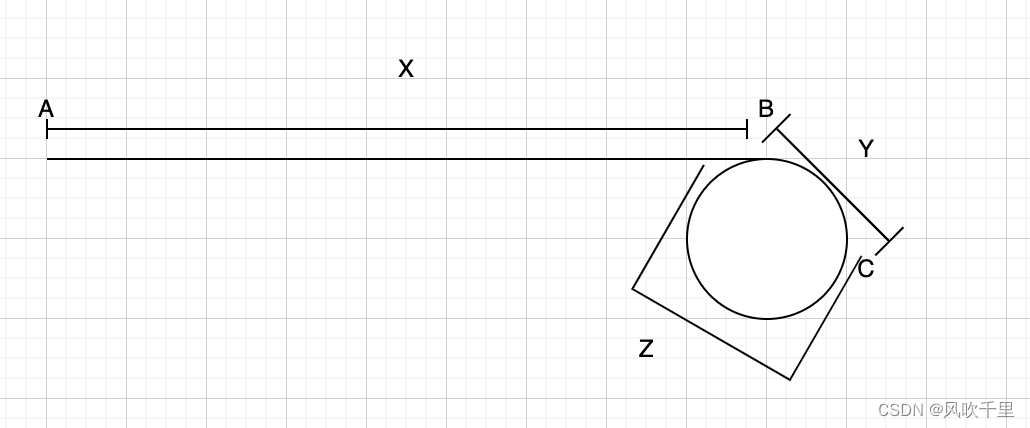
根据下图分析计算,C为fast和slow指针第一次相遇的点。可知从C到B与从A到B以相同速度走第一次相遇的节点一定为B,即为入口点。解法二的实现,如下。
代码实现
public class Node<V> {public Node<V> pre;public Node<V> next;private V v;public Node(V v) {this.v = v;}public V getV() {return v;}public void setV(V v) {this.v = v;}
}
public static Node<Integer> entryNodeOfLoop(Node<Integer> head) {if (head == null || head.next == null){return null;}Node<Integer> fast = head;Node<Integer> slow = head;while (fast !=null && fast.next !=null){fast = fast.next.next;slow = slow.next;if (slow == fast){break;}}// 若是快指针指向null,则不存在环if(fast == null || fast.next == null)return null;// 重新指向链表头部fast = head;while (fast !=slow){fast = fast.next;slow = slow.next;}return fast;
}
从C到B与从A到B以相同速度走第一次相遇的节点一定为B?
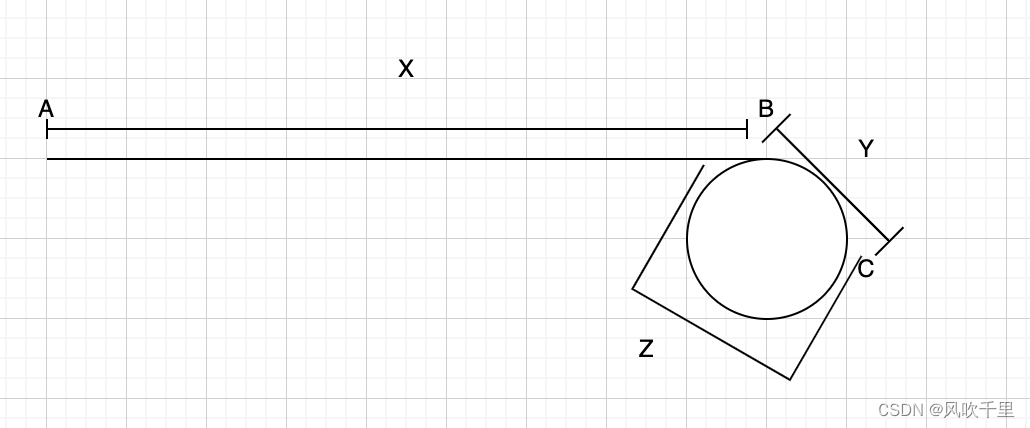
我们用数学的方式证明一下。
如果结论:A到B走和C到B顺时针相同速度走,第一次相遇的点一定为B点。成立
那么数学表达式有 X = n(Y+Z)+Z n>=0,n为环的圈数;的结论成立为证明A到B走和C到B顺时针相同速度走,第一次相遇的点一定为B点
即证明:X = n(Y+Z)+Z n>=0;n为环的圈数由第一次相遇在C点得:2(X+Y) = X + w(Y+Z) + Y;(w>=1,w为环的圈数)
推导:==> 2(X+Y) = X + w(Y+Z) + Y + Z + Y;(w>=0,w为环的圈数)==> 2(X+Y) = X + w(Y+Z) + 2Y + Z;(w>=0,w为环的圈数)==> X = w(Y+Z) +Z ;(w>=0,w为环的圈数)所以:X = n(Y+Z)+Z n>=0;n为环的圈数。成立即:A到B走和C到B顺时针相同速度走,第一次相遇的点一定为B点。
相关文章:

链表中环的入口节点
链表中环的入口节点 描述 链表中环的入口节点 给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。 数据范围: n≤10000, 1<结点值<10000 要求:空间复杂度 O(1)…...

STL——函数对象,谓词
一、函数对象 1.函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象。 函数对象使用重载的()时,行为类似函数调用,也叫仿函数。 本质: 函数对象(仿函数)是一个类,不是一个函数。 2.函数对象…...

【区分vue2和vue3下的element UI Descriptions 描述列表组件,分别详细介绍属性,事件,方法如何使用,并举例】
在 Element UI(为 Vue 2 设计)和 Element Plus(为 Vue 3 设计)中,Descriptions(描述列表)组件通常用于展示一系列的结构化信息。然而,需要明确的是,Element UI 官方库中并…...

atcoder abc 358
A welcome to AtCoder Land 题目: 思路:字符串比较 代码: #include <bits/stdc.h>using namespace std;int main() {string a, b;cin >> a >> b;if(a "AtCoder" && b "Land") cout <&…...
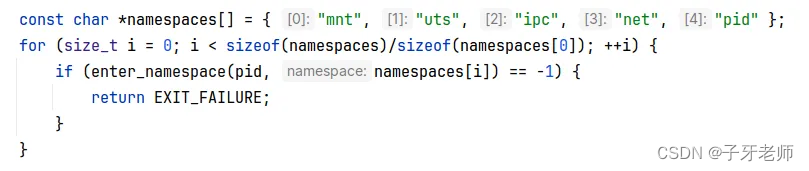
手写docker:你先玩转namespace再来吧
哈喽,我是子牙老师。今天咱们聊聊Linux namespace 瓦特?你没听过namespace?那有必要科普一下了:namespace是Linux内核提供的一种软件性质的资源隔离机制。容器化技术,比如docker,就是基于这样的机制实现的…...

注册安全分析报告:PingPong
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞 …...
)
mysqladmin——MySQL Server管理程序(二)
mysqladmin 是一个命令行工具,用于执行简单的 MySQL 服务器管理任务,如检查服务器的状态、创建和删除数据库、重载权限等。 1 reload 重新加载授权表(grant tables)。当修改了MySQL的权限系统(例如,修改了…...

Microsoft Edge无法启动搜索问题的解决
今天本来想清一下电脑,看到visual studio2022没怎么用了就打算卸载掉。然后看到网上有篇文章说进入C盘的ProgramFiles(x86)目录下的microsoft目录下的microsoft visual studio目录下的install目录中,双击InstallCleanup.exe&#…...

Appium Android 自动化测试 -- 元素定位
自动化测试元素定位是难点之一,编写脚本时会经常卡在元素定位这里,有时一个元素能捣鼓一天,到最后还是定位不到。 Appium 定位方式和 selenium 一脉相承,selenium 中的定位方式Appium 中都支持,而 Appium 还增加了自己…...

C#.net6.0+Vue+Ant-Design智慧医院手术麻醉系统源码 手术麻醉软件信息化管理系统 麻醉文书祥解
C#.net6.0VueAnt-Design智慧医院手术麻醉系统源码 手术麻醉软件信息化管理系统 麻醉文书祥解 医护人员通过手麻信息系统可以进行手术的预约申请、受理、安排,从门诊医生下医嘱到发起手术申请、护士长审核通过,均实现了全流程信息化管理,大大…...

6G时代,即将来临!
日前,由未来移动通信论坛、紫金山实验室主办的2024全球6G技术大会在南京召开。本次大会以“创新预见6G未来”为主题,在大会开幕式上发布了协力推进全球6G统一标准行动的倡议和紫金山科技城加速培育以6G技术引领未来产业行动计划。 在我国已开展第五代移动…...
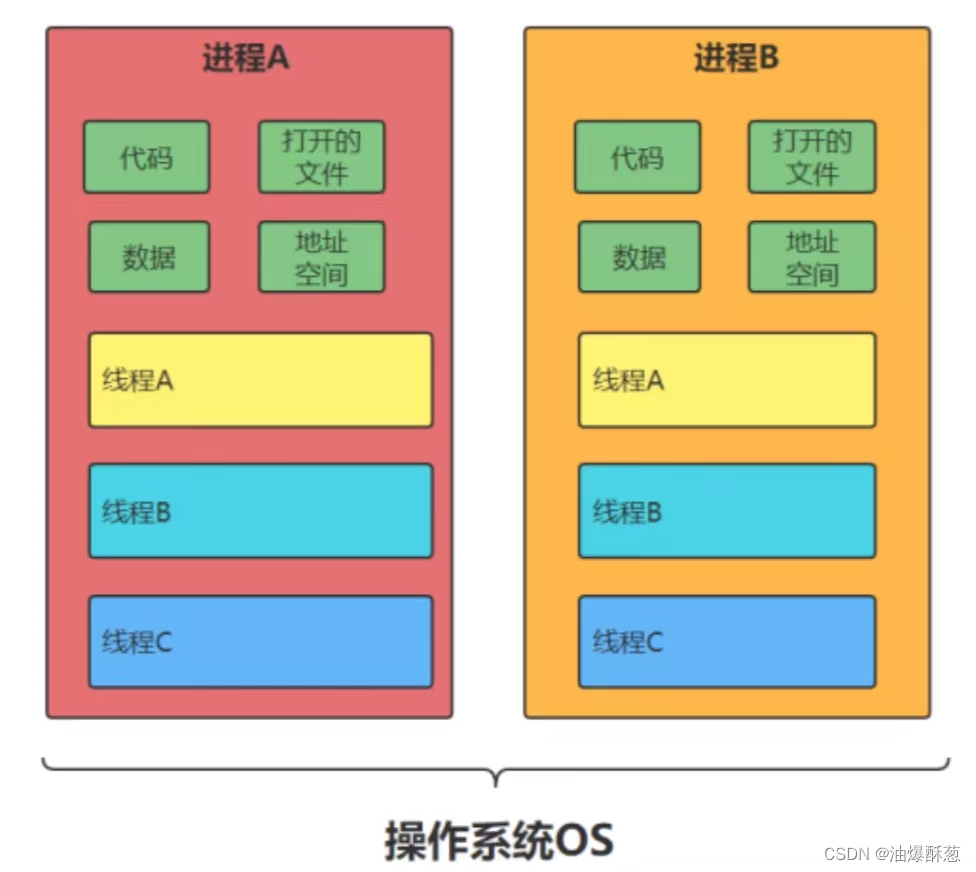
进程、线程的区别
进程、线程的关系 开工厂生产手机,制作一条生产线,这个生产线上有很多的器件以及材料。一条生产线就是一个进程。 只有生产线是不够的,使用找五个工人来进行生产,这个工人能够利用这些材料最终一步步的将手机做出来,这…...

JWT详解、JWTUtil工具类的构建方法
一、前言 使用一些用户不友好的项目时,会发现,每一次进入网站,我们都要重新登录。 这是为什么呢? 现代多采用前后端分离的项目架构,这种架构,前后端使用不同的服务器,两个服务器上存储的信息不…...
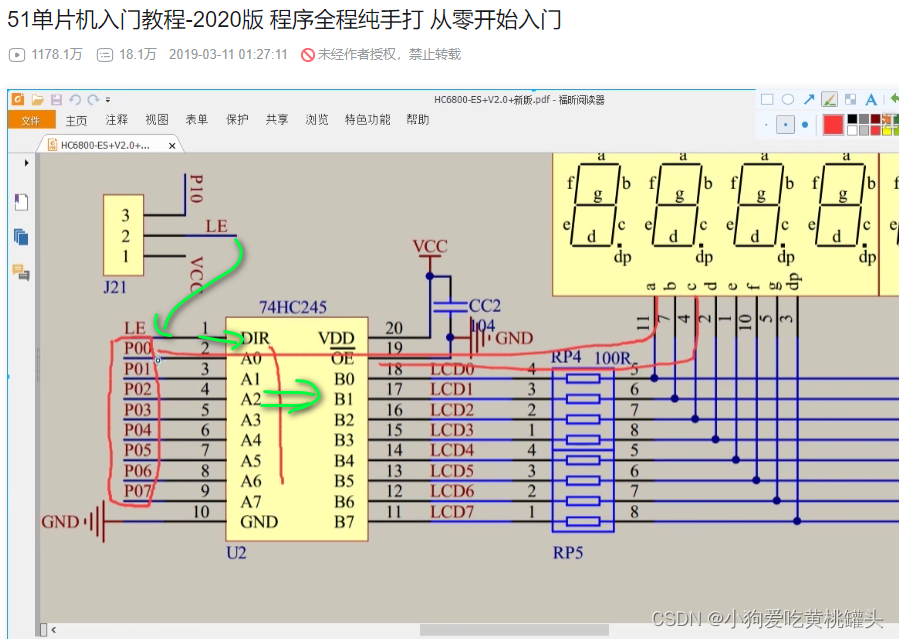
江协科技51单片机学习- p11 静态数码管显示
前言: 本文是根据哔哩哔哩网站上“江协科技51单片机”视频的学习笔记,在这里会记录下江协科技51单片机开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了江协科技51单片机教学视频和链接中的内容。 引用: 51单片机入门教程-2…...

pandas.frame输出parquet
代码 import pandas as pd import pyarrow._parquet as pqdata pd.read_parquet("0000.parquet") total_rows len(data) half_row_num total_rows//2 print(half_row_num) first_half data.iloc[:20000] second_half data.iloc[20000:20000] # print(first_hal…...

【CT】LeetCode手撕—42. 接雨水
目录 题目1- 思路2- 实现⭐42. 接雨水——题解思路 3- ACM实现 题目 原题连接:42. 接雨水 1- 思路 模式识别:求雨水的面积 ——> 不仅是只求一个比当前元素大的元素,还要求面积 单调栈 应用场景,需要找到左边比当前元素大的…...

GPT-4o一夜被赶超,Claude 3.5一夜封王|快手可灵大模型推出图生视频功能|“纯血”鸿蒙大战苹果AI|智谱AI“钱途”黯淡|月之暗面被曝进军美国
快手可灵大模型推出图生视频功能“纯血”鸿蒙大战苹果AI,华为成败在此一举大模型低价火拼间,智谱AI“钱途”黯淡手握新“王者”,腾讯又跟渠道干上了“美食荒漠”杭州,走出一个餐饮IPOGPT-4o一夜被赶超,Anthropic推出Cl…...
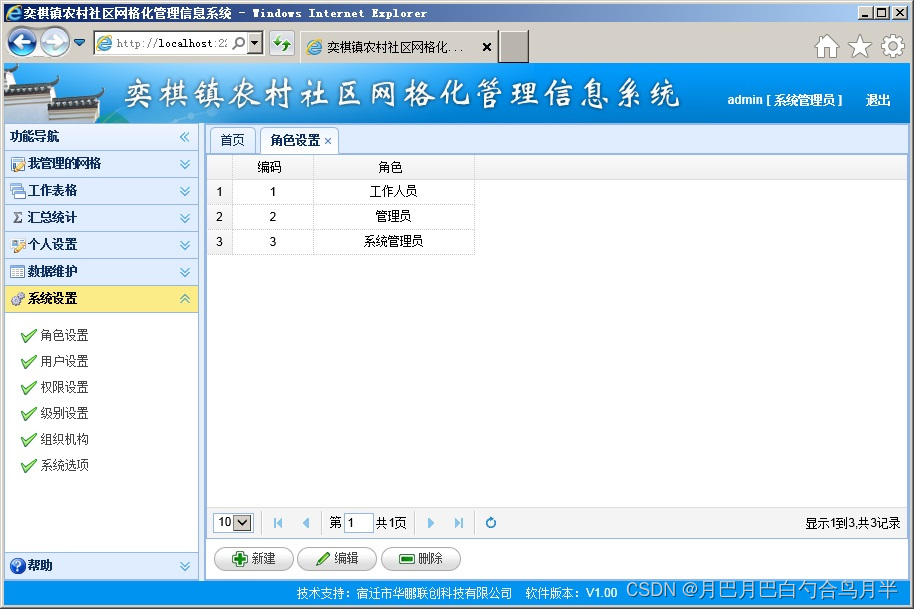
C# + easyui 写的一个web项目
用C# easyui 来开发,其实就是为了开发速度,用easyui可以一天写很多页面,比一些低代码平台还快。 登陆页面 主界面 记录数统计 家庭信息采集表 新建家庭 家庭成员 低保、五保人员帮扶情况登记表 低保、五保人员帮扶情况登记表的新增和编辑 治…...
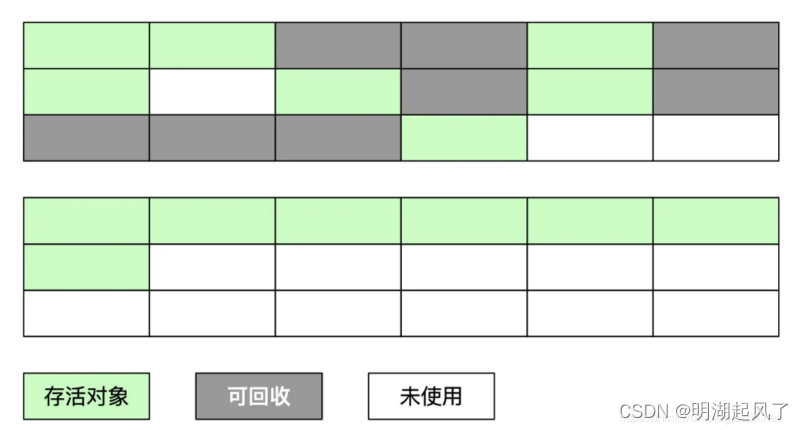
JVM 垃圾回收分配及算法
一、判断对象是否可以回收 垃圾收集器在做垃圾回收的时候,首先需要判定的就是哪些内存是需要被回收 的,哪些对象是「存活」的,是不可以被回收的;哪些对象已经「死掉」了,需 要被回收。 一般有两种方法来判断ÿ…...

尚品汇-(四)
(1)商品的基本知识 1.1基本信息—分类 一般情况可以分为两级或者三级。咱们的项目一共分为三级,即一级分类、二级分类、三级分类。 比如:家用电器是一级分类,电视是二级分类,那么超薄电视就是三级分类。…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...
