AcWing 255. 第K小数
自己想出来的,感觉要容易想到,使用可持久化线段树,时间上要比y的慢一倍。大体思想就是,我们从小到大依次加入一个数,每加入一个就记录一个版本,线段树里记录区间里数的数量,在查询时,只要二分出区间数的数量大于等于k的最小版本即可,这个版本对应插入的点就是要求的第 k 小点,时间复杂度是 O ( n log 2 n ) O(n\log^2n) O(nlog2n) 的和 y 是一个量级的,可能是由于常数问题,所以运行上要慢。
题目链接
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cmath>using namespace std;const int N = 100010;int n, m;
int idx, root[N], cnt;
int g[N];struct node
{int v, id;bool operator<(const node &W)const{return v < W.v;}
}a[N];struct Node
{int l, r;int v, sum = 0;
}tr[N * 4 + N * (int)ceil(log2(N))];void pushup(int u)
{int &l = tr[u].l, &r = tr[u].r;tr[u].sum = tr[l].sum + tr[r].sum;
}int build(int l, int r)
{int p = ++ idx;if (l == r){tr[p].v = -0x3f3f3f3f;tr[p].sum = 0;return p;}int mid = l + r >> 1;tr[p].l = build(l, mid);tr[p].r = build(mid + 1, r);pushup(p);return p;
}int insert(int p, int l, int r, int x, int k)
{int q = ++ idx;tr[q] = tr[p];if (l == r){tr[q].v = k;if (k > -0x3f3f3f3f) tr[q].sum = 1;return q;}int mid = l + r >> 1;if (x <= mid) tr[q].l = insert(tr[p].l, l, mid, x, k);else tr[q].r = insert(tr[p].r, mid + 1, r, x, k);pushup(q);return q;
}int query(int p, int l, int r, int x, int y)
{if (x <= l && r <= y) return tr[p].sum;int mid = l + r >> 1;int sum = 0;if (x <= mid) sum += query(tr[p].l, l, mid, x, y);if (y > mid) sum += query(tr[p].r, mid + 1, r, x, y);return sum;
}bool check(int x, int l, int r, int k)
{return query(root[x], 1, n, l, r) >= k;
}int main()
{cin >> n >> m;root[0] = build(1, n);for (int i = 1; i <= n; i ++ ) {int x;scanf("%d", &x);a[i] = {x, i};g[i] = x;}sort(a + 1, a + n + 1);for (int i = 1; i <= n; i ++ ) {root[i] = insert(root[i - 1], 1, n, a[i].id, a[i].v);// cout << i << endl;}while (m -- ){int ls, rs, k;scanf("%d%d%d", &ls, &rs, &k);int l = 0, r = n, mid;while (l < r){mid = l + r >> 1;if (check(mid, ls, rs, k)) r = mid;else l = mid + 1;}printf("%d\n", a[l].v);}// cout << query(root[5], 1, n, 2, 5);return 0;}
相关文章:

AcWing 255. 第K小数
自己想出来的,感觉要容易想到,使用可持久化线段树,时间上要比y的慢一倍。大体思想就是,我们从小到大依次加入一个数,每加入一个就记录一个版本,线段树里记录区间里数的数量,在查询时,…...

Nginx - 反向代理、负载均衡、动静分离、底层原理(案例实战分析)
目录 Nginx 开始 概述 安装(非 Docker) 配置环境变量 常用命令 配置文件概述 location 路径匹配方式 配置反向代理 实现效果 准备工作 具体配置 效果演示 配置负载均衡 实现效果 准备工作 具体配置 实现效果 其他负载均衡策略 配置动…...

从零开始精通Onvif之用户管理
💡 如果想阅读最新的文章,或者有技术问题需要交流和沟通,可搜索并关注微信公众号“希望睿智”。 概述 用户管理是Onvif协议的重要组成部分,它允许系统管理员通过网络接口创建、删除、修改用户账户,并分配不同的权限&am…...
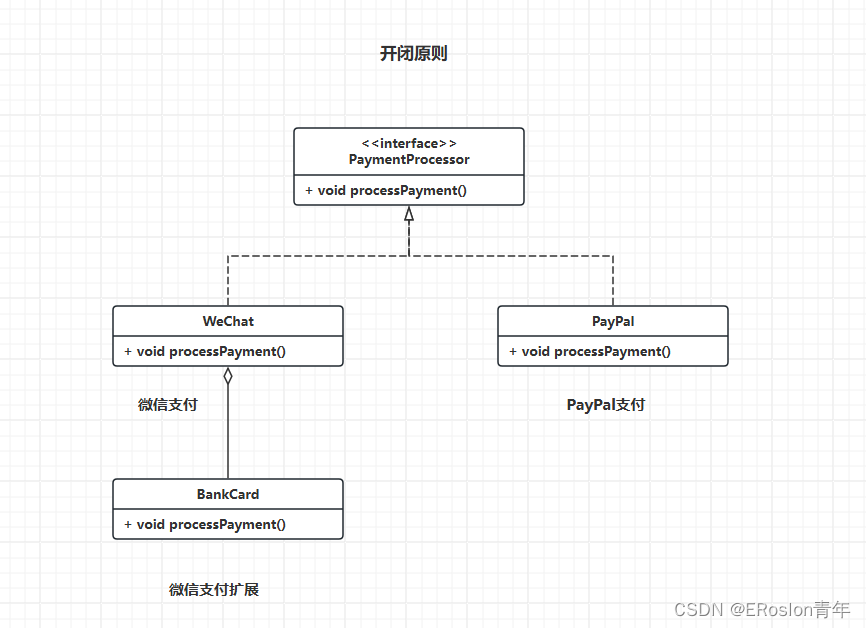
设计模式——设计模式原则
设计模式 设计模式示例代码库地址: https://gitee.com/Jasonpupil/designPatterns 设计模式原则 单一职责原则(SPS): 又称单一功能原则,面向对象五个基本原则(SOLID)之一 原则定义…...
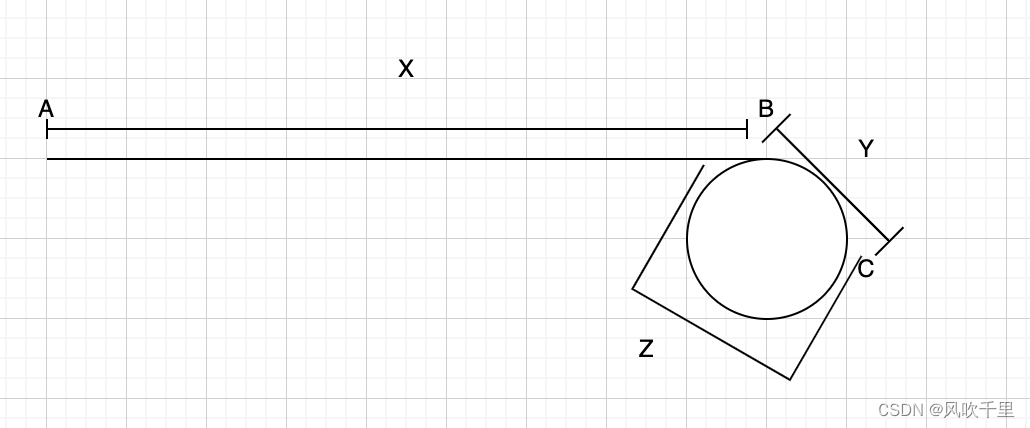
链表中环的入口节点
链表中环的入口节点 描述 链表中环的入口节点 给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。 数据范围: n≤10000, 1<结点值<10000 要求:空间复杂度 O(1)…...

STL——函数对象,谓词
一、函数对象 1.函数对象概念 概念: 重载函数调用操作符的类,其对象常称为函数对象。 函数对象使用重载的()时,行为类似函数调用,也叫仿函数。 本质: 函数对象(仿函数)是一个类,不是一个函数。 2.函数对象…...

【区分vue2和vue3下的element UI Descriptions 描述列表组件,分别详细介绍属性,事件,方法如何使用,并举例】
在 Element UI(为 Vue 2 设计)和 Element Plus(为 Vue 3 设计)中,Descriptions(描述列表)组件通常用于展示一系列的结构化信息。然而,需要明确的是,Element UI 官方库中并…...

atcoder abc 358
A welcome to AtCoder Land 题目: 思路:字符串比较 代码: #include <bits/stdc.h>using namespace std;int main() {string a, b;cin >> a >> b;if(a "AtCoder" && b "Land") cout <&…...
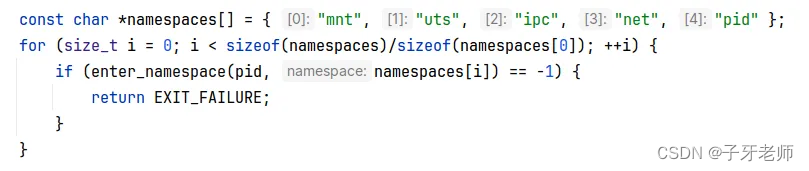
手写docker:你先玩转namespace再来吧
哈喽,我是子牙老师。今天咱们聊聊Linux namespace 瓦特?你没听过namespace?那有必要科普一下了:namespace是Linux内核提供的一种软件性质的资源隔离机制。容器化技术,比如docker,就是基于这样的机制实现的…...

注册安全分析报告:PingPong
前言 由于网站注册入口容易被黑客攻击,存在如下安全问题: 暴力破解密码,造成用户信息泄露短信盗刷的安全问题,影响业务及导致用户投诉带来经济损失,尤其是后付费客户,风险巨大,造成亏损无底洞 …...
)
mysqladmin——MySQL Server管理程序(二)
mysqladmin 是一个命令行工具,用于执行简单的 MySQL 服务器管理任务,如检查服务器的状态、创建和删除数据库、重载权限等。 1 reload 重新加载授权表(grant tables)。当修改了MySQL的权限系统(例如,修改了…...

Microsoft Edge无法启动搜索问题的解决
今天本来想清一下电脑,看到visual studio2022没怎么用了就打算卸载掉。然后看到网上有篇文章说进入C盘的ProgramFiles(x86)目录下的microsoft目录下的microsoft visual studio目录下的install目录中,双击InstallCleanup.exe&#…...

Appium Android 自动化测试 -- 元素定位
自动化测试元素定位是难点之一,编写脚本时会经常卡在元素定位这里,有时一个元素能捣鼓一天,到最后还是定位不到。 Appium 定位方式和 selenium 一脉相承,selenium 中的定位方式Appium 中都支持,而 Appium 还增加了自己…...

C#.net6.0+Vue+Ant-Design智慧医院手术麻醉系统源码 手术麻醉软件信息化管理系统 麻醉文书祥解
C#.net6.0VueAnt-Design智慧医院手术麻醉系统源码 手术麻醉软件信息化管理系统 麻醉文书祥解 医护人员通过手麻信息系统可以进行手术的预约申请、受理、安排,从门诊医生下医嘱到发起手术申请、护士长审核通过,均实现了全流程信息化管理,大大…...

6G时代,即将来临!
日前,由未来移动通信论坛、紫金山实验室主办的2024全球6G技术大会在南京召开。本次大会以“创新预见6G未来”为主题,在大会开幕式上发布了协力推进全球6G统一标准行动的倡议和紫金山科技城加速培育以6G技术引领未来产业行动计划。 在我国已开展第五代移动…...
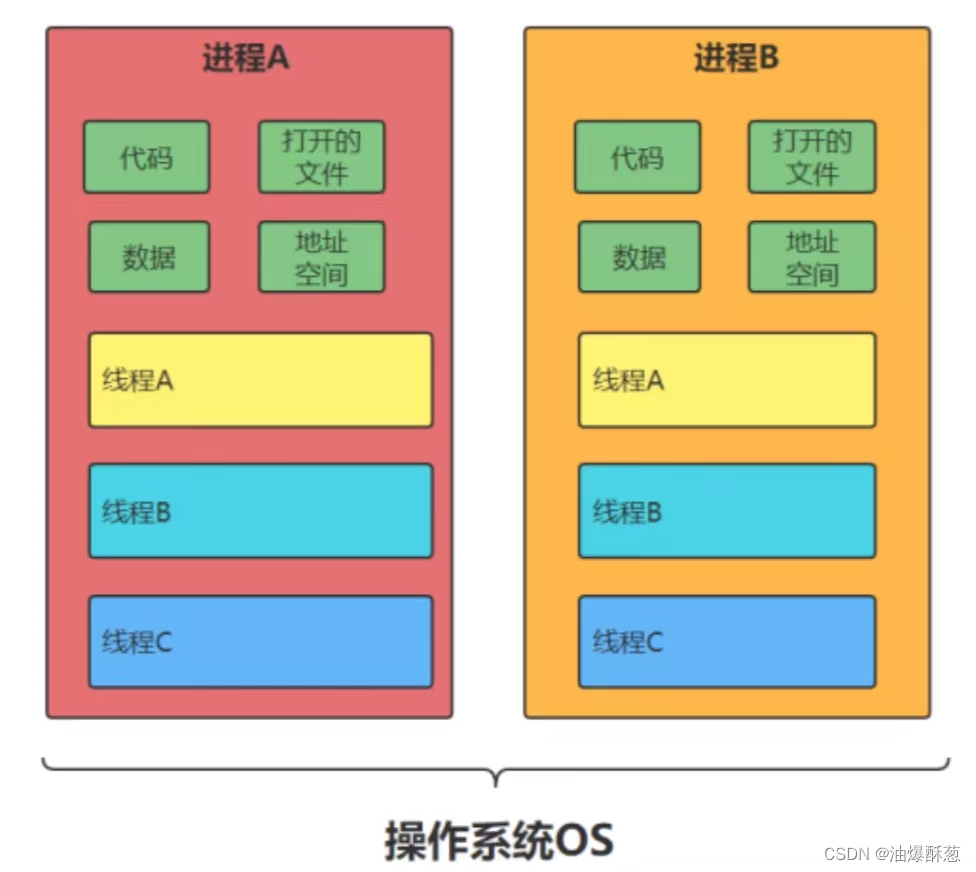
进程、线程的区别
进程、线程的关系 开工厂生产手机,制作一条生产线,这个生产线上有很多的器件以及材料。一条生产线就是一个进程。 只有生产线是不够的,使用找五个工人来进行生产,这个工人能够利用这些材料最终一步步的将手机做出来,这…...

JWT详解、JWTUtil工具类的构建方法
一、前言 使用一些用户不友好的项目时,会发现,每一次进入网站,我们都要重新登录。 这是为什么呢? 现代多采用前后端分离的项目架构,这种架构,前后端使用不同的服务器,两个服务器上存储的信息不…...
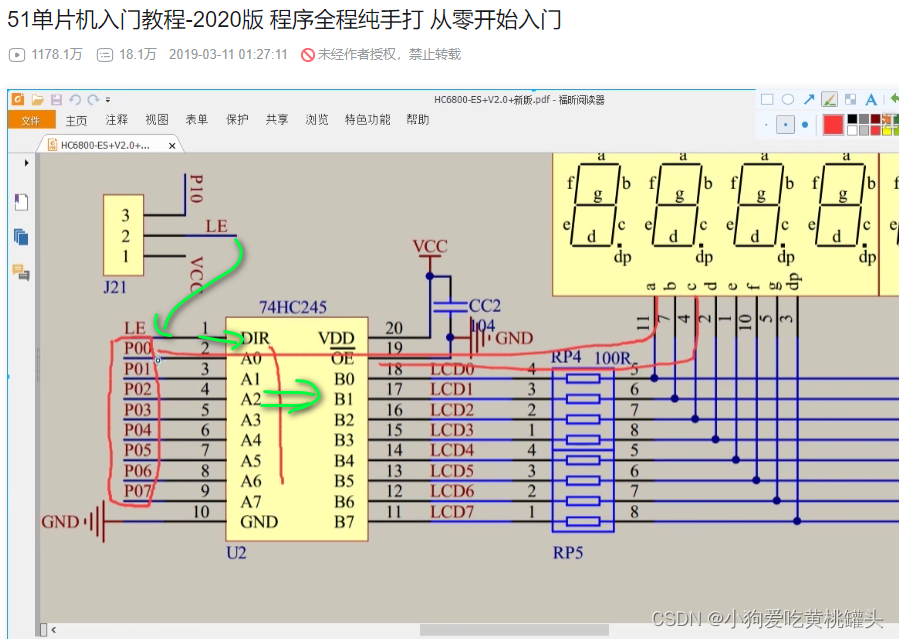
江协科技51单片机学习- p11 静态数码管显示
前言: 本文是根据哔哩哔哩网站上“江协科技51单片机”视频的学习笔记,在这里会记录下江协科技51单片机开发板的配套视频教程所作的实验和学习笔记内容。本文大量引用了江协科技51单片机教学视频和链接中的内容。 引用: 51单片机入门教程-2…...

pandas.frame输出parquet
代码 import pandas as pd import pyarrow._parquet as pqdata pd.read_parquet("0000.parquet") total_rows len(data) half_row_num total_rows//2 print(half_row_num) first_half data.iloc[:20000] second_half data.iloc[20000:20000] # print(first_hal…...

【CT】LeetCode手撕—42. 接雨水
目录 题目1- 思路2- 实现⭐42. 接雨水——题解思路 3- ACM实现 题目 原题连接:42. 接雨水 1- 思路 模式识别:求雨水的面积 ——> 不仅是只求一个比当前元素大的元素,还要求面积 单调栈 应用场景,需要找到左边比当前元素大的…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

消防一体化安全管控平台:构建消防“一张图”和APP统一管理
在城市的某个角落,一场突如其来的火灾打破了平静。熊熊烈火迅速蔓延,滚滚浓烟弥漫开来,周围群众的生命财产安全受到严重威胁。就在这千钧一发之际,消防救援队伍迅速行动,而豪越科技消防一体化安全管控平台构建的消防“…...
