26、matlab多项式曲线拟合:polyfit ()函数
1、前言
在 MATLAB 中,可以使用 polyfit() 函数进行多项式曲线拟合。polyfit() 函数可以拟合一个多项式模型到给定的数据点,从而找到最符合这些数据点的多项式曲线。以下是关于 polyfit() 函数的一些基本说明和示例用法:
语法
p = polyfit(x, y, n)x和y是数据点的横纵坐标,分别为列向量。n是要拟合的多项式的阶数。p返回拟合多项式的系数,按照从高次到低次排列。
示例用法
% 生成一些带噪声的数据点
x = 1:10; y = 2*x + 1 + randn(1, 10);
% 使用 polyfit 进行二次曲线拟合
p = polyfit(x, y, 2); y_fit = polyval(p, x);
% 可视化结果
scatter(x, y, 'b'); % 显示原始数据点
hold on; plot(x, y_fit, 'r'); % 显示拟合曲线在以上示例中,我们首先生成了一些带有噪声的数据点 x 和 y。然后使用 polyfit() 函数拟合了一个二次多项式模型到这些数据点,并计算了拟合的曲线上的点 y_fit。最后,使用 scatter() 和 plot() 函数进行可视化,展示了原始数据点和拟合曲线。
通过 polyfit() 函数,我们可以方便地进行多项式曲线拟合,从而对数据进行模型化和分析。根据数据的特点可以选择不同次数的多项式来进行拟合,以获得较好的拟合效果。
2、polyfit 多项式曲线拟合
简介
polyfit函数是numpy中的一个多项式拟合函数,它用于拟合给定数据点的多项式曲线。多项式拟合是一种常见的数据拟合方法,通过拟合一个高阶的多项式函数来逼近实际数据点的分布。
polyfit函数的基本语法为:
如下所示
其中,x和y是数据点的x坐标和y坐标,degree是多项式的阶数。函数返回一个包含多项式系数的数组,这些系数可以用来构建多项式拟合曲线。coefficients数组中的元素分别代表多项式的各个项的系数,从高次到低次排列。
通过使用polyfit函数,我们可以得到一个拟合数据点的多项式曲线,从而用来预测或者分析数据的趋势。需要注意的是,多项式拟合可能会出现过拟合或者欠拟合的情况,因此在选择多项式的阶数时需要小心。
语法
语法:p = polyfit(x,y,n) 返回次数为 n 的多项式 p(x) 的系数,该
相关文章:
函数)
26、matlab多项式曲线拟合:polyfit ()函数
1、前言 在 MATLAB 中,可以使用 polyfit() 函数进行多项式曲线拟合。polyfit() 函数可以拟合一个多项式模型到给定的数据点,从而找到最符合这些数据点的多项式曲线。以下是关于 polyfit() 函数的一些基本说明和示例用法: 语法 p = polyfit(x, y, n) x 和 y 是数据点的横纵…...

VMR,支持30+种编程语言的SDK版本管理器,支持Windows/MacOS/Linux。
官方文档地址:https://docs.vmr.us.kg/ 欢迎安装使用,分享转发,前往github star。 跨平台,支持Windows,Linux,MacOS支持多种语言和工具,省心受到lazygit的启发,拥有更友好的TUI&…...

模板初阶【C++】
文章目录 模板的作用模板的原理模板分为两大类——函数模板和类模板函数模板语法函数模板实例化模板函数的方式模板函数的类型转换既有函数模板又有已经实现的函数,会优先调用哪一个? 类模板语法模板类实例化对象模板类的模板参数可以有缺省值类模板中的…...
搭建Vue的环境
目录 # 开篇 步骤一,准备Vue 的环境 步骤二,下载Vue.js的包 步骤三,创建并打开写前端代码的文件夹 步骤四,在VSCode中引入Vue.js的包 步骤五,创建第一个vue.html Vue其他知识 Vue.config命令 # 开篇 介绍&…...

[学习笔记]-MyBatis-Plus简介
简介 Mybatis-Plus(简称 MP)是一个 MyBatis (opens new window)的增强工具,在 MyBatis 的基础上只做增强不做改变,为简化开发、提高效率而生。 简言之就是对单表的增删改查有了很好的封装。基本不用再单独写sql语句了。目前此类…...

2024.6.23 刷题总结
2024.6.23 **每日一题** 520.检测大写字母,本题是简单模拟题,考察了ASCLL码相关的知识,根据题意,本题对于字符串有三种正确的用法,所以我们分三类来讨论,先根据首字母的大小写来分类,如果首字母…...
的最新一条记录)
mysql查询不同用户(操作记录)的最新一条记录
先用MAX(time) 和 group by item_id 查询出不同的item_id对应的最大时间,然后再在外面连表查询,查询 表中 item_id 和login_time 时间 相等于刚才的查询记录的记录 具体语句如下 select a.* from reyo a join (select item_id,max(login_time) as ti…...

Java中如何使用设计模式来解决编程问题?
Java中使用设计模式来解决编程问题,可以显著提高代码的可复用性、可维护性和可读性。设计模式是一套被广泛应用于软件工程的解决方案,描述了在特定上下文中面对具体问题时的可复用解决方案。以下是几种常用的设计模式及其应用场景: 单例模式…...
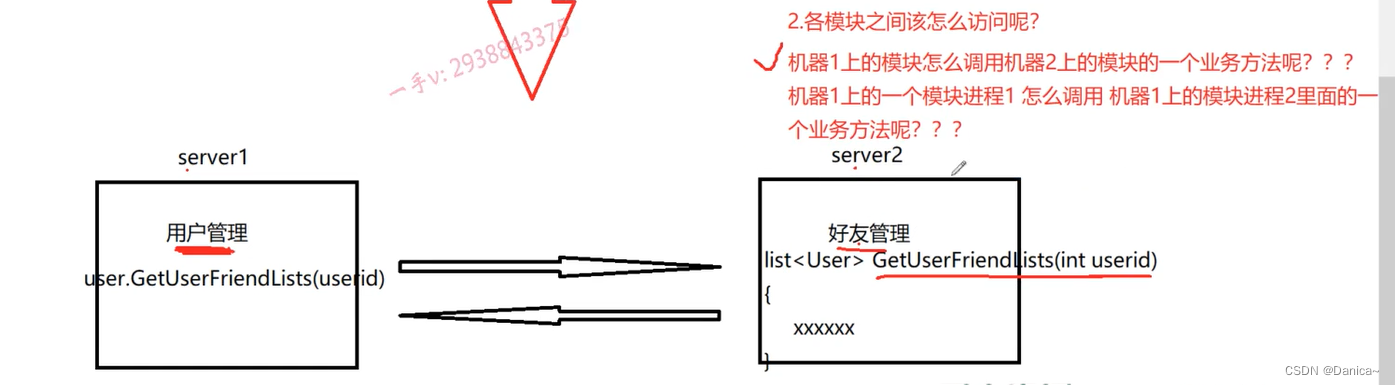
单机、集群和分布式
目录 1.概述 2.单机服务器 单机版的服务器的性能,设计上的瓶颈? 3.集群 解决瓶颈1: 没有解决瓶颈2: 没有解决瓶颈3: 集群的优点? 集群的缺点? 4.分布式 分布式的优点? 分…...
qt开发-10_LineEdit
QLineEdit 小部件是一个单行文本编辑器。行编辑允许用户使用一组有用的编辑函数输入和 编辑一行纯文本。包括撤消和重做、剪切和粘贴以及拖放。通过更改行编辑的 echoMode(),它 还可以用作“只写”字段,用于输入如密码等. 创建好项目后,进入 …...
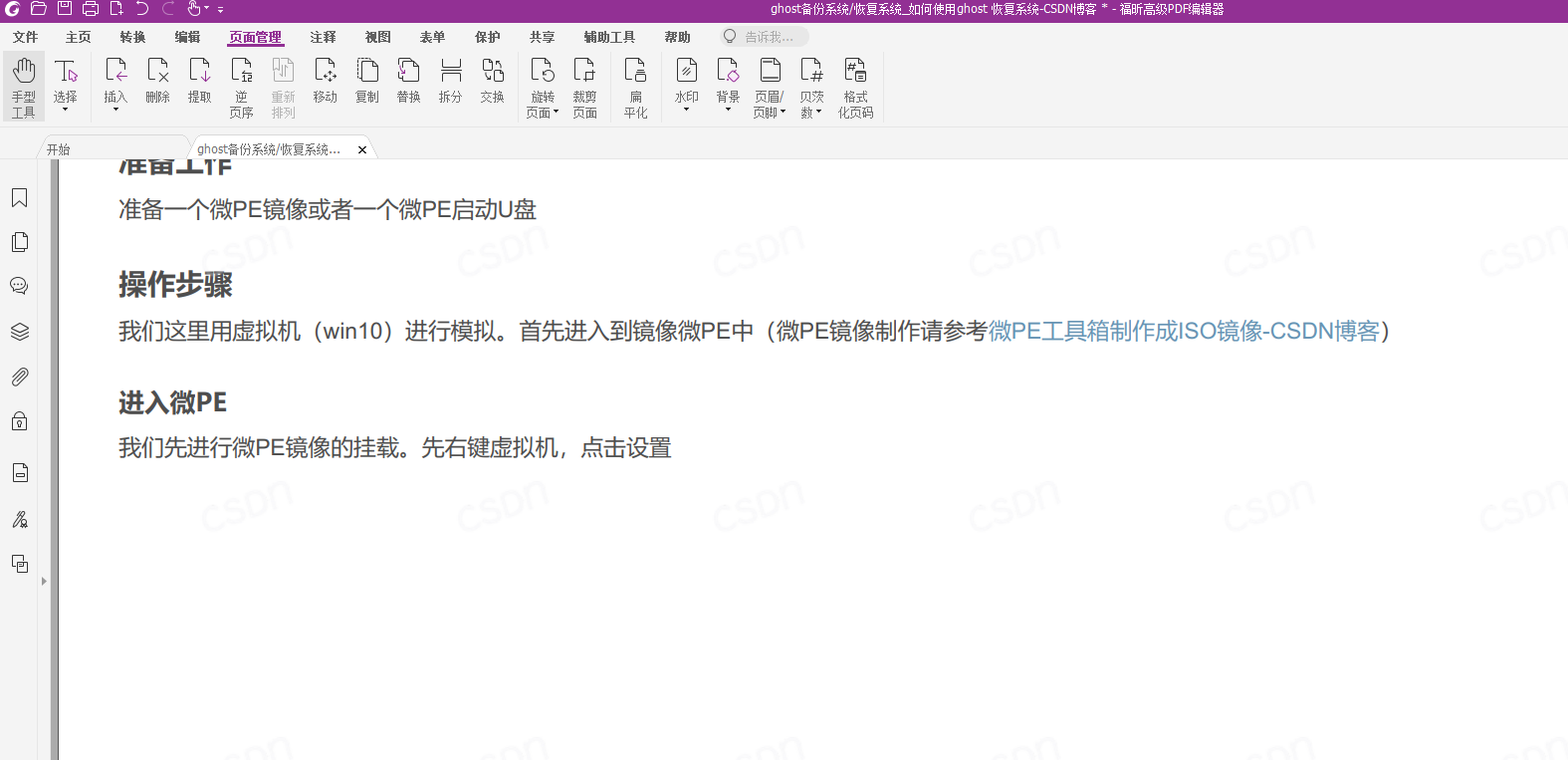
福昕PDF编辑器快速去除PDF水印方法
在福昕PDF编辑器软件中打开一个带有水印的PDF文件,点击如图下所示的页面管理->水印,点击全部移除 点击 是 水印消除(注:部分类型的水印可以消除,但是有些类型的水印无法通过此方法消除)...

Cloudflare 常用操作
一、域名托管到cloudflare 登录cloudflare->添加站点->填写域名(例如阿里云)->继续选择free套餐->继续->保存cloudflare分配的DNS地址->进入阿里云域名管理->进入DNS管理/DNS修改把DNS地址修改为cloudflare分配的两个DNS->保存->回到cloudflare->…...
,展开时合起上一次展开的内容,始终保持展开内容为一个,并且再次点击合起自身)
elementUI的table使用展开功能( type=“expand“ ),展开时合起上一次展开的内容,始终保持展开内容为一个,并且再次点击合起自身
直接上代码了没什么可讲的,主要是用到 row-key"id" :expand-row-keys"expands row-click"handleRowClick" <template><div class"ele-body"><el-card shadow"never"><!-- 数据表格 --><ele-pro-t…...
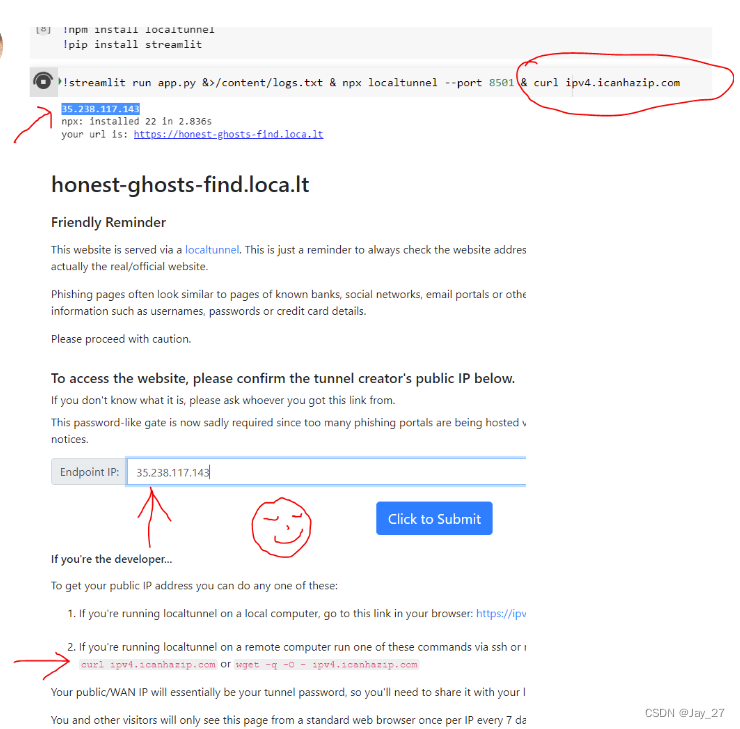
【金】?Y? python网页前端streamlit
1、如何从 Google Colab Notebook 启动 streamit参考-How to Launch Streamlit App from Google Colab Notebook !streamlit run web.py & npx localtunnel --port 8501 & curl ipv4.icanhazip.com...

数据仓库之Lambda架构
Lambda架构是一种设计大规模数据处理系统的架构模式,它结合了批处理和实时处理的优点,以应对大数据的多样性、速度和规模问题。该架构主要由三个层次组成:批处理层(Batch Layer)、速度层(Speed Layer&#…...

Apriori 处理ALLElectronics事务数据
通过Apriori算法挖掘以下事务集合的频繁项集: 流程图 代码 # 导入必要的库 from itertools import combinations# 定义Apriori算法函数 def apriori(transactions, min_support, min_confidence):# 遍历数据,统计每个项的支持度 item_support {}for tr…...

Content Provider:深入解析Android数据共享的核心组件
在Android开发中,Content Provider是一个重要的组件,它允许应用程序之间共享数据。它扮演着“数据访问中间层”的角色,为不同应用程序提供了一个统一的数据访问接口。以下将从技术难点、面试官关注点、回答吸引力以及代码举例四个方面&#x…...

069、Python 函数的递归调用
函数可以自己调用自己吗??? 这就涉及函数的递归的用法了。 递归的概念: 函数递归是指函数在其定义中直接或间接调用自身的过程。 递归是一种强有力的编程技术,通常用于解决可以被分解为相同问题的子问题的情况&…...

数仓开发那些事_番外
一位神州的正式员工(没错,就是之前文章中出现的实习生):一闪,你今年涨工资了吗? 一闪:mad,一年辛苦到头只涨了500米 神州员工:你去年绩效不是优秀吗,怎么就涨…...

Vue3+TypeScript项目实战——打造雨雪交加的智慧城市
个人简介 👀个人主页: 前端杂货铺 ⚡开源项目: rich-vue3 (基于 Vue3 TS Pinia Element Plus Spring全家桶 MySQL) 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 …...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

关于 WASM:1. WASM 基础原理
一、WASM 简介 1.1 WebAssembly 是什么? WebAssembly(WASM) 是一种能在现代浏览器中高效运行的二进制指令格式,它不是传统的编程语言,而是一种 低级字节码格式,可由高级语言(如 C、C、Rust&am…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...
