内容安全复习 6 - 白帽子安全漏洞挖掘披露的法律风险
文章目录
- 安全漏洞的法律概念界定
- 安全漏洞特征
- 白帽子
- 安全漏洞挖掘面临的法律风险
- “白帽子”安全漏洞挖掘的风险根源
- “白帽子”的主体边界
- 授权行为边界
- 关键结论

安全漏洞的法律概念界定
- 可以被利用来破坏所在系统的网络或信息安全的缺陷或错误;
被利用的网络缺陷、错误 - 任何可能有助于对安全控制造成破坏的硬件、软件、流程或者程序;
用来破坏的软硬件程序 - 计算机信息系统在需求、设计、实现、配置、运行等过程中,有意或无意产生的缺陷。
系统产生的缺陷
安全漏洞特征
- 可以利用的资源特征;
- 难以避免的缺陷属性;
- 普遍存在的属性;
- 长久存在的属性。
白帽子
- 降低经济损失;
- 促进产业创新和技术发展;
- 维护网络安全。
安全漏洞挖掘面临的法律风险
- 漏洞发现可能产生“侵入”的法律刑事责任;
- “白帽子”的法律地位不明确;
- 缺少对授权行为边界及构成要件的详细指引;
- 众测平台的合规性有待强化。
“白帽子”安全漏洞挖掘的风险根源
- 行为边界不明确;
- 法律地位缺失;
- 平台合规性有待强化。
“白帽子”的主体边界
- 建立“白帽子”官方加密保护的实名身份认证注册制度,准予注册后为其颁发唯一识别的代号,“白帽子”凭识别代号进行众测活动。
注册 - 通过行业规范强化“白帽子”的道德感和职业操守,明确其行为的法律边界;
职业道德、法律边界 - 规范众测平台在企业和“白帽子”间的枢纽和链接功能。
规范职能
授权行为边界
- 众测平台模式下,拥有平台注册用户资格的“白帽子”身份并不视为取得当然授权;
- 平台规则并不等同于授权,应基于众测平台与企业之间签署任何委托或合同所明示的内容为授权限定范围;
实际授权范围取决于合同内容,而不仅仅是大的规则。 - 漏洞挖掘并不等同于漏洞披露的授权,禁止未经众测平台同意和企业明确确认的安全漏洞披露;
未经同意不能披露漏洞。 - 漏洞挖掘并不等同于漏洞修复的授权,禁止发布未经众测平台验证的漏洞修复工具/补丁;
未经同意不能发布漏洞补丁。 - 授权具有时限性,禁止在现有法律和保密协议规定范围之外实施漏洞测试、评估等。
关键结论
- 只有主观上维护网络安全,且具有实名认证基础的漏洞发现者才可能成为合法主体。
- 取得合法授权是安全漏洞发现行为的合法前提,但准予漏洞发现的授权不应泛化,同样应当基于必要的限制。
相关文章:

内容安全复习 6 - 白帽子安全漏洞挖掘披露的法律风险
文章目录 安全漏洞的法律概念界定安全漏洞特征白帽子安全漏洞挖掘面临的法律风险“白帽子”安全漏洞挖掘的风险根源“白帽子”的主体边界授权行为边界关键结论 安全漏洞的法律概念界定 可以被利用来破坏所在系统的网络或信息安全的缺陷或错误;被利用的网络缺陷、错…...

dp经典问题:爬楼梯
dp经典问题:爬楼梯 爬楼梯 三步问题。有个小孩正在上楼梯,楼梯有n阶台阶,小孩一次可以上1阶、2阶或3阶。实现一种方法,计算小孩有多少种上楼梯的方式。结果可能很大,你需要对结果模1000000007。 Step1: 识别问题 这…...
示例:推荐一个基于第三方QRCoder.Xaml封装的二维码显示控件
一、目的:基于第三方QRCoder.Xaml封装的二维码控件,为了方便WPF调用 二、效果如下 功能包括:背景色,前景色,中心图片设置和修改大小,二维码设置等 三、环境 VS2022 四、使用方式 1、安装nuget包…...

阿里云服务器618没想到这么便宜,买早了!
2年前,我买了个服务器,租用服务器(ECS5)和网络宽带(1M),可以说是非常非常低的配置了。 当时5年的折扣力度最大,但是打完折后,价格依然要近3000多元。 最近看到阿里云618活…...

提升Python技能的七个函数式编程技巧
文章目录 📖 介绍 📖🏡 演示环境 🏡📒 文章内容 📒📝 递归📝 结构化模式匹配📝 不变性📝 纯函数📝 高阶函数📝 函数组合📝 惰性求值⚓️ 相关链接 ⚓️📖 介绍 📖 在现代编程中,虽然Python并不是一门纯粹的函数式编程语言,但函数式编程(Funct…...
微型操作系统内核源码详解系列五(五):cm3下Pendsv切换任务上篇
系列一:微型操作系统内核源码详解系列一:rtos内核源码概论篇(以freertos为例)-CSDN博客 系列二:微型操作系统内核源码详解系列二:数据结构和对象篇(以freertos为例)-CSDN博客 系列…...

Django测试平台搭建学习笔记1
一安装 pip离线安装requests2.32.0所需要的依赖: : charset-normalizer<4,>2 (3.0.0b1) : idna<4,>2.5 (3.7) : urllib3<3,>1.21.1 (2.2.0) : certifi>2017.4.17 (2024.6.2) pip离线安装pytest8.2.0所需要的依赖: : iniconfig (2…...
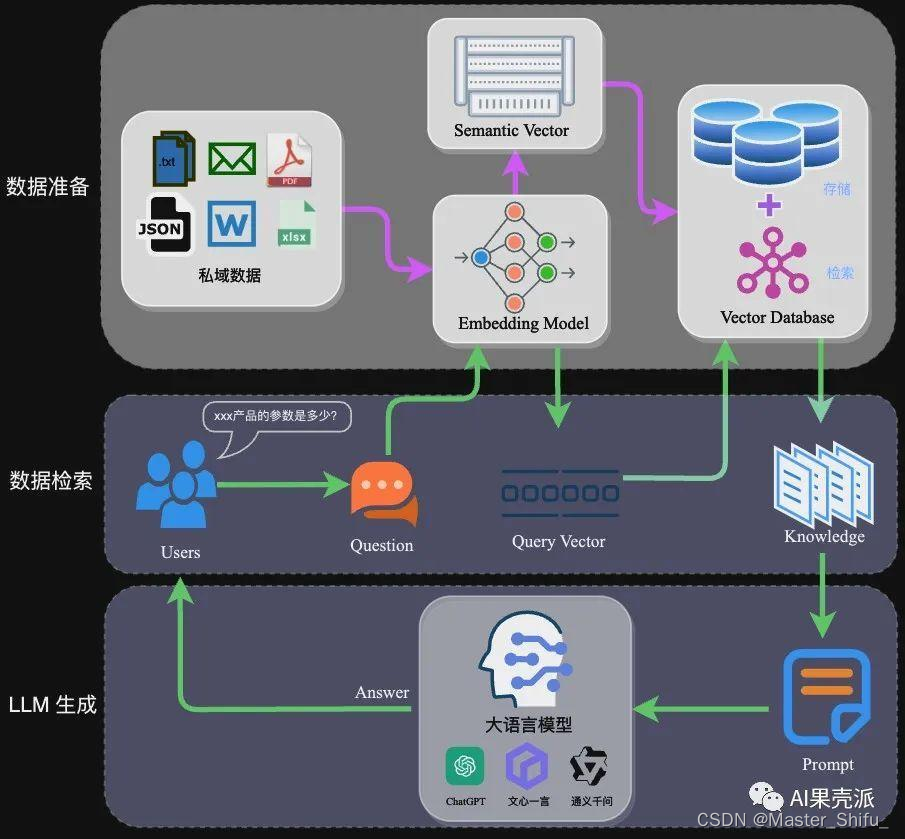
本地离线模型搭建指南-RAG架构实现
搭建一个本地中文大语言模型(LLM)涉及多个关键步骤,从选择模型底座,到运行机器和框架,再到具体的架构实现和训练方式。以下是一个详细的指南,帮助你从零开始构建和运行一个中文大语言模型。 本地离线模型搭…...

【IPython 使用技巧整理】
IPython 使用技巧整理 IPython 是一个交互式 Python 解释器,比标准 Python 解释器提供了更加强大的功能和更友好的使用体验。它为数据科学、机器学习和科学计算提供了强大的工具,是 Python 开发人员不可或缺的工具之一。本文将深入探讨 IPython 的各种使…...
什么是孪生素数猜想
什么是孪生素数猜想 素数p与素数p2有无穷多对 孪生素数的公式(详见百度百科:孪生素数公式) 利用素数的判定法则,可以得到以下的结论:“若自然数q与q2都不能被任何不大于的素数 整除,则q与q 2都是素数”…...
Python学习笔记16:进阶篇(五)异常处理
异常 在编程中,异常是指程序运行过程中发生的意外事件,这些事件通常中断了正常的指令流程。它们可能是由于错误的输入数据、资源不足、非法操作或其他未预料到的情况引起的。Python中,当遇到这类情况时,会抛出一个异常对象&#…...

Mac 安装依赖后依旧报错 ModuleNotFoundError: No module named ‘Crypto‘
ModuleNotFoundError: No module named ‘Crypto’ 解决办法 pip uninstall pycryptodome pip uninstall pycrypto pip uninstall crypto pip install pycrypto...

【07】持久化-数据库选择和设计
1. 数据库选择 在比特币原始论文中,并没有提到要使用哪一个具体的数据库,它完全取决于开发者如何选择。Bitcoin Core ,最初由中本聪发布,现在是比特币的一个参考实现,它使用的是 LevelDB。 我们将要使用的是BoltDB。Bolt DB是一个纯键值存储的 Go 数据库。没有具体的数据…...
压力测试
1.什么是压力测试 压力测试考察当前软硬件环境下系统所能承受的最大负荷并帮助找出系统瓶颈所在。压测都是为了系统在线上的处理能力和稳定性维持在一个标准范围内,做到心中有数 使用压力测试,我们有希望找到很多种用其他测试方法更难发现的错误&#…...
C语言| 数组元素的删除
同数组元素的插入差不多。 数组元素的插入,是先移动要插入元素位置后面的所有元素,再插入新元素,长度1。 C语言| 数组的插入-CSDN博客 数组元素的删除,是先删除元素,再把后面的元素往前移动一位,而本程序…...
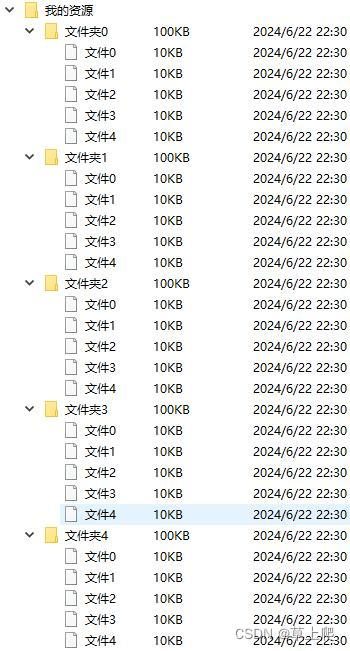
QListView、QTableView或QTreeView截取滚动区域(截长图)
本文以QTreeView为例,理论上继承自QAbstractScrollArea的类都支持本文所述的方法。 一.效果 一共5个文件夹,每个文件文件夹下有5个文件,先把文件夹展开,然后截图。将滚动条拖到居中位置,是为了证明截图对滚动条无影响 下面是截的图 二.原理 将滚动区域的viewport设置为…...

论文《Tree Decomposed Graph Neural Network》笔记
【TDGNN】本文提出了一种树分解方法来解决不同层邻域之间的特征平滑问题,增加了网络层配置的灵活性。通过图扩散过程表征了多跳依赖性(multi-hop dependency),构建了TDGNN模型,该模型可以灵活地结合大感受场的信息&…...

控制下属很简单,用好这3大管人绝招,再跳的刺头也不敢造次
控制下属很简单,用好这3大管人绝招,再跳的刺头也不敢造次 第一招:给压力 很多团队中的员工都是自己不带脑子工作,遇事就喜欢请示领导,让领导拿方案、拿决策。 还有一些人,推一下,他才动一下&a…...
2.APP测试-安卓adb抓取日志
1.打开手机的开发者模式,打开USB调试 (1)小米手机打开开发者模式: 【设置】-【我的设备】-【全部参数信息】-快速多次点击【OS版本】-进入开发者模式 (2)连接手机和电脑,手机打开USB调试 【设置…...
高考填报志愿选专业,要善于发掘自身优势
每年的高考季,如何填报志愿又再成为困扰家长以及学生的难题,可能在面对大量的专业时,无论是考生还是家长都不知道应该如何选择,好的专业孩子不一定有优势,感兴趣的冷门专业又担心日后找工作难。 实际上,专业…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...
