什么是孪生素数猜想
什么是孪生素数猜想
素数p与素数p+2有无穷多对
孪生素数的公式(详见百度百科:孪生素数公式)
利用素数的判定法则,可以得到以下的结论:“若自然数q与q+2都不能被任何不大于的素数 整除,则q与q + 2都是素数”。这是因为一个自然数n是素数当且仅当它不能被任何小于等于
的素数整除。 用数学的语言表示以上的结论,就是:
存在一组自然数
,
使得
.......(1)
其中 表示从小到大排列时的前k个素数:2,3,5,....。并且满足
1≦ i ≦ k,
,
.
这样解得的自然数q如果满足,
则q与q+2是一对孪生素数。
我们可以把(1)式的内容等价转换成为同余方程组表示:
q ≡ (mod
), q ≡
(mod
), ..., q ≡
(mod
).....(2)
由于(2)的模都是素数,因此两两互素,根据孙子定理(中国剩余定理)知,对于给定的
,(2)式有唯一 一个小于
的正整数解。
范例
例如k=1时,
,
解得q=3, 5。由于,所以可知3与3+2、5与5+2都是孪生素数。这样就求得了区间(3,
)里的全部孪生素数对。
又比如k=2时,
列出方程
,
解得q=5,11,17。由于17<,所以11与11+2、17与17+2都是了孪生素数。由于这已经是所有可能的
值,所以这样就求得了区间(5,
)的全部孪生素数对。
| k=3时 | |||
|---|---|---|---|
| 11 ;41 | 17 | 29 |
由于这已经是所有可能的值,所以这样就求得了区间(7,
)的全部孪生素数对。
| k=4时 | 7m4+2 | 7m4+3 | 7m4+4 | 7m4+6 | |
|---|---|---|---|---|---|
| 71 | 191 | 101 | 11 | 41 | |
| 197 | 107 | 17 | 137 | 167 | |
| 29 | 149 | 59 | 179 | 209 |
由于这已经是所有可能的值,所以这样就求得了区间(11,
)的全部孪生素数对(8个小于121-2的解)。 仿此下去可以一个不漏地求得任意大的数以内的全部孪生素数对。
结论推广
孪生素数猜想就是在k值任意大时(1)和(2)式都有小于的解。问题已经转入初等数论范围。 参考文献,孪生质数公式,【中等数学】2000年1期
相关文章:
什么是孪生素数猜想
什么是孪生素数猜想 素数p与素数p2有无穷多对 孪生素数的公式(详见百度百科:孪生素数公式) 利用素数的判定法则,可以得到以下的结论:“若自然数q与q2都不能被任何不大于的素数 整除,则q与q 2都是素数”…...
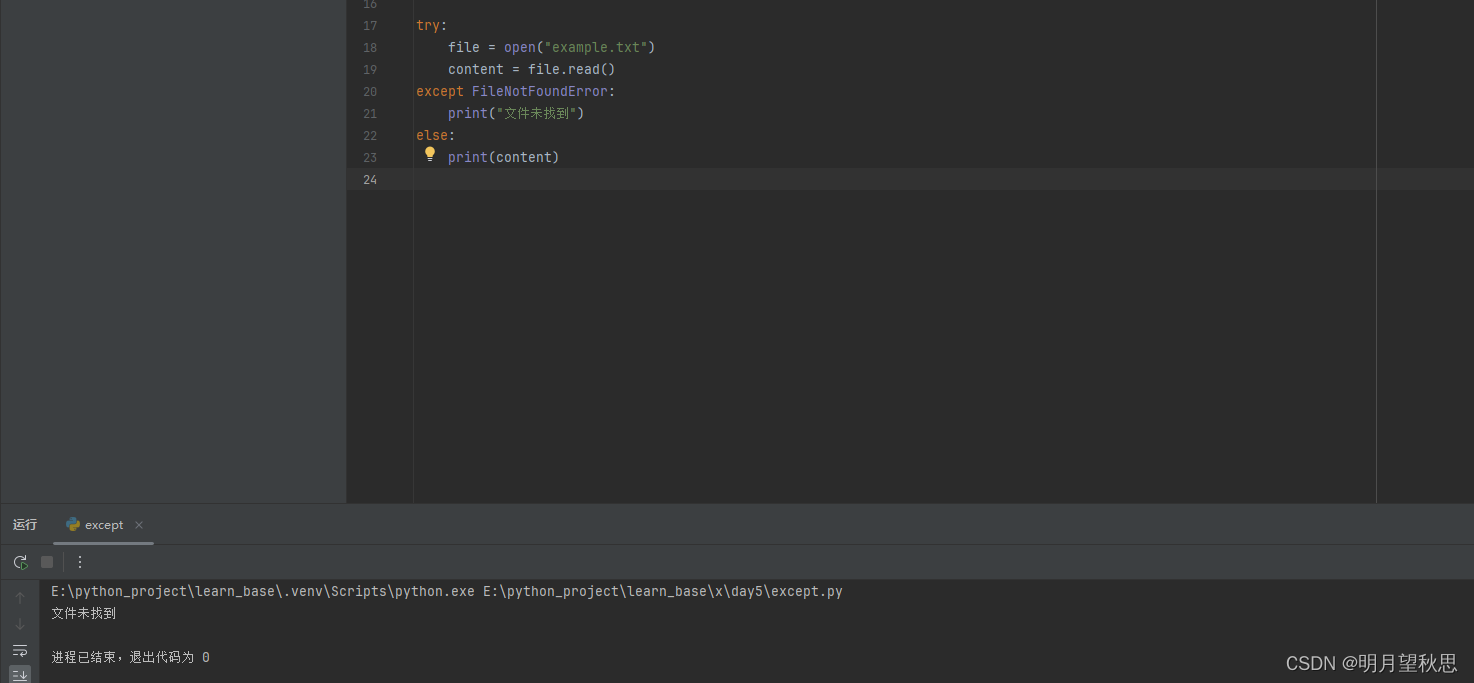
Python学习笔记16:进阶篇(五)异常处理
异常 在编程中,异常是指程序运行过程中发生的意外事件,这些事件通常中断了正常的指令流程。它们可能是由于错误的输入数据、资源不足、非法操作或其他未预料到的情况引起的。Python中,当遇到这类情况时,会抛出一个异常对象&#…...

Mac 安装依赖后依旧报错 ModuleNotFoundError: No module named ‘Crypto‘
ModuleNotFoundError: No module named ‘Crypto’ 解决办法 pip uninstall pycryptodome pip uninstall pycrypto pip uninstall crypto pip install pycrypto...

【07】持久化-数据库选择和设计
1. 数据库选择 在比特币原始论文中,并没有提到要使用哪一个具体的数据库,它完全取决于开发者如何选择。Bitcoin Core ,最初由中本聪发布,现在是比特币的一个参考实现,它使用的是 LevelDB。 我们将要使用的是BoltDB。Bolt DB是一个纯键值存储的 Go 数据库。没有具体的数据…...
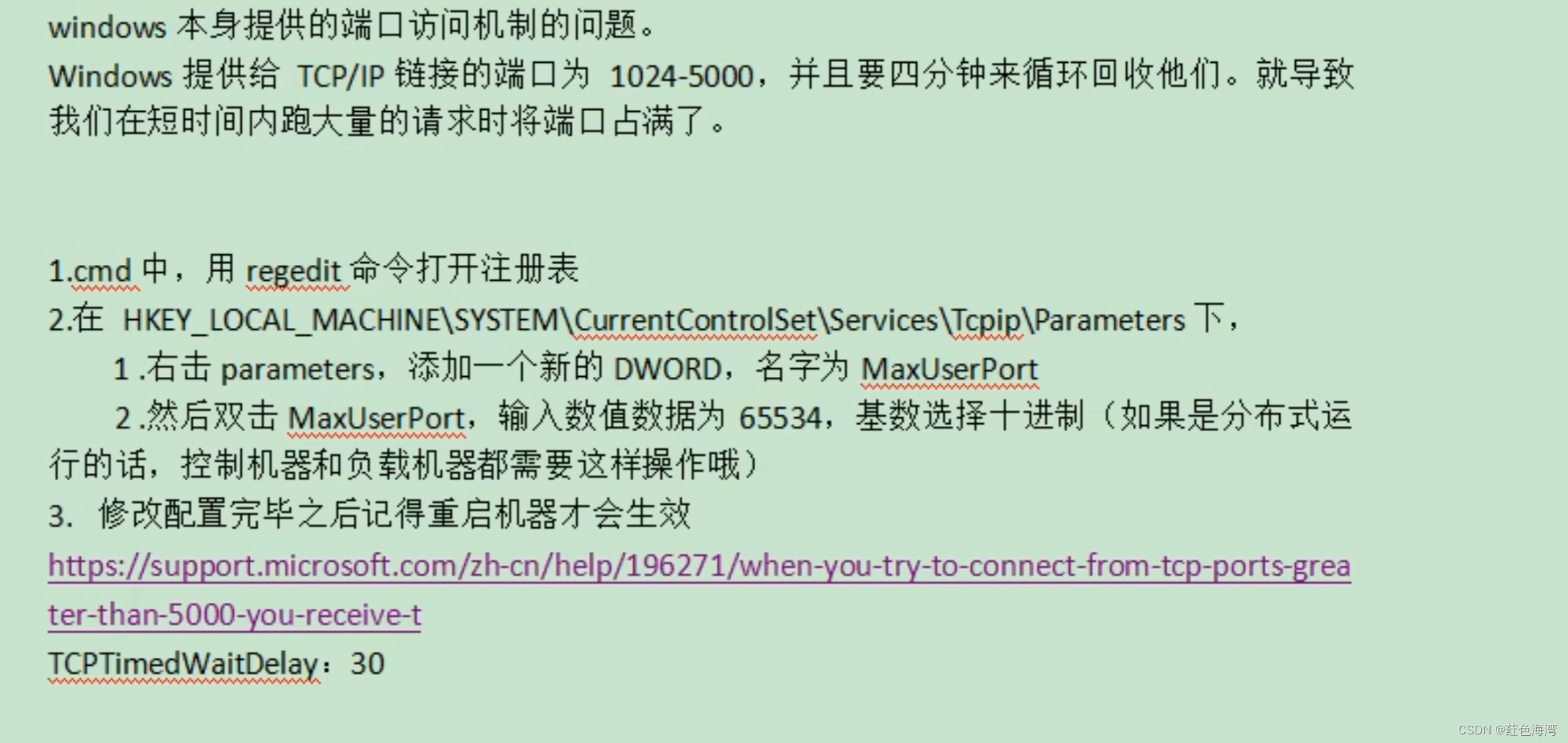
压力测试
1.什么是压力测试 压力测试考察当前软硬件环境下系统所能承受的最大负荷并帮助找出系统瓶颈所在。压测都是为了系统在线上的处理能力和稳定性维持在一个标准范围内,做到心中有数 使用压力测试,我们有希望找到很多种用其他测试方法更难发现的错误&#…...
C语言| 数组元素的删除
同数组元素的插入差不多。 数组元素的插入,是先移动要插入元素位置后面的所有元素,再插入新元素,长度1。 C语言| 数组的插入-CSDN博客 数组元素的删除,是先删除元素,再把后面的元素往前移动一位,而本程序…...
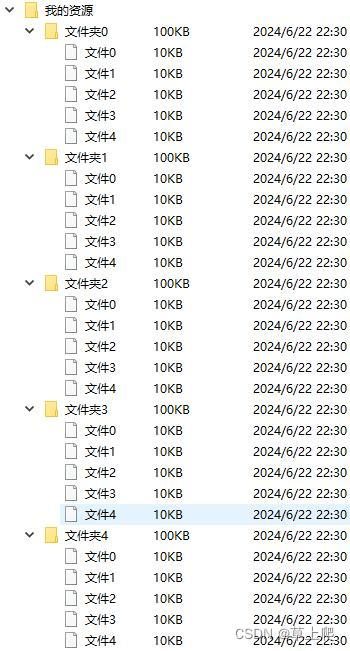
QListView、QTableView或QTreeView截取滚动区域(截长图)
本文以QTreeView为例,理论上继承自QAbstractScrollArea的类都支持本文所述的方法。 一.效果 一共5个文件夹,每个文件文件夹下有5个文件,先把文件夹展开,然后截图。将滚动条拖到居中位置,是为了证明截图对滚动条无影响 下面是截的图 二.原理 将滚动区域的viewport设置为…...

论文《Tree Decomposed Graph Neural Network》笔记
【TDGNN】本文提出了一种树分解方法来解决不同层邻域之间的特征平滑问题,增加了网络层配置的灵活性。通过图扩散过程表征了多跳依赖性(multi-hop dependency),构建了TDGNN模型,该模型可以灵活地结合大感受场的信息&…...

控制下属很简单,用好这3大管人绝招,再跳的刺头也不敢造次
控制下属很简单,用好这3大管人绝招,再跳的刺头也不敢造次 第一招:给压力 很多团队中的员工都是自己不带脑子工作,遇事就喜欢请示领导,让领导拿方案、拿决策。 还有一些人,推一下,他才动一下&a…...
2.APP测试-安卓adb抓取日志
1.打开手机的开发者模式,打开USB调试 (1)小米手机打开开发者模式: 【设置】-【我的设备】-【全部参数信息】-快速多次点击【OS版本】-进入开发者模式 (2)连接手机和电脑,手机打开USB调试 【设置…...
高考填报志愿选专业,要善于发掘自身优势
每年的高考季,如何填报志愿又再成为困扰家长以及学生的难题,可能在面对大量的专业时,无论是考生还是家长都不知道应该如何选择,好的专业孩子不一定有优势,感兴趣的冷门专业又担心日后找工作难。 实际上,专业…...

如何在 Ubuntu 14.04 上使用 HAProxy 实现 SSL 终止
前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。点击跳转到网站。 简介 HAProxy,全称高可用代理,是一款流行的开源软件 TCP/HTTP 负载均衡器和代理解决方案,可在 Linu…...

dockercompose
安装dockerconpose #上传docker-compose安装包 chmod x docker-compose mv docker-compose /usr/bin/ [rootlocalhost ~]# docker-compose --version docker-compose version 1.24.1, build 4667896b文件格式以及编写注意事项 YAML 是一种标记语言,它可以很直观的…...

「51媒体」活动会议,展览展会,直播曝光的一种方法
传媒如春雨,润物细无声,大家好,我是51媒体网胡老师。 我们在做活动会议,或者参加展览展会,需要进行直播的时候,可以通过一键同步多个媒体平台的方法,来扩大曝光,比如一场直播我们可…...
Go WebSocket入门+千万级别弹幕系统架构设计
Go实现WebSocket(千万级别弹幕系统架构设计) 1 websocket简介(基于HTTP协议的长连接) 使用WebSocket可以轻松的维持服务器端长连接,其次WebSocket是架构在HTTP协议之上的,并且也可以使用HTTPS方式,因此WebSocket是可靠…...

uniapp使用伪元素实现气泡
uniapp使用伪元素实现气泡 背景实现思路代码实现尾巴 背景 气泡效果在开发中使用是非常常见的,使用场景有提示框,对话框等等,今天我们使用css来实现气泡效果。老规矩,先看下效果图: 实现思路 其实实现这个气泡框的…...
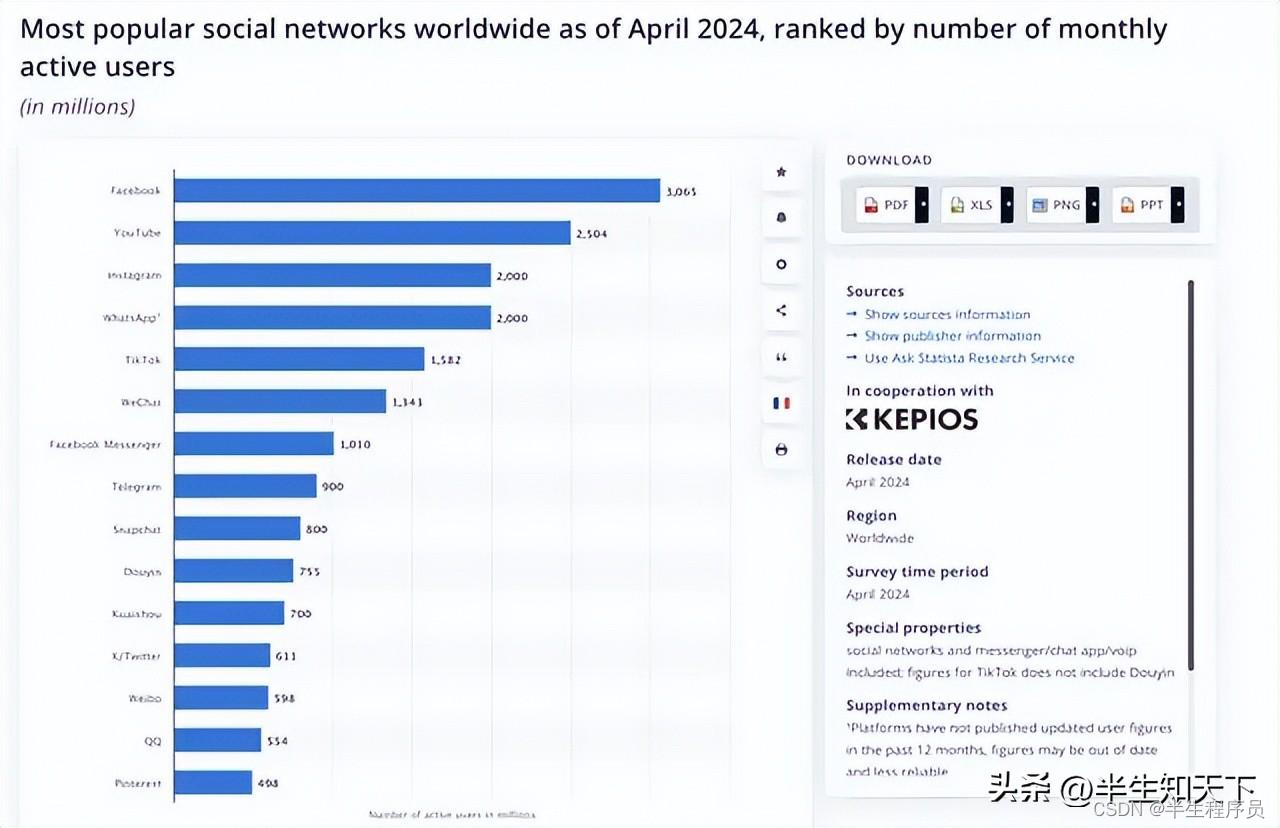
字节跳动:从梦想之芽到参天大树
字节跳动掌舵人:张一鸣 2012年:梦想的起点:在一个阳光明媚的早晨,北京的一座普通公寓里,一位名叫张一鸣的年轻人坐在电脑前,眼中闪烁着坚定的光芒。他的心中有一个梦想——通过技术改变世界,让…...

组合数学、圆排列、离散数学多重集合笔记
自用 如果能帮到您,那也值得高兴 知识点 离散数学经典题目 多重集合组合 补充容斥原理公式 隔板法题目 全排列题目:...
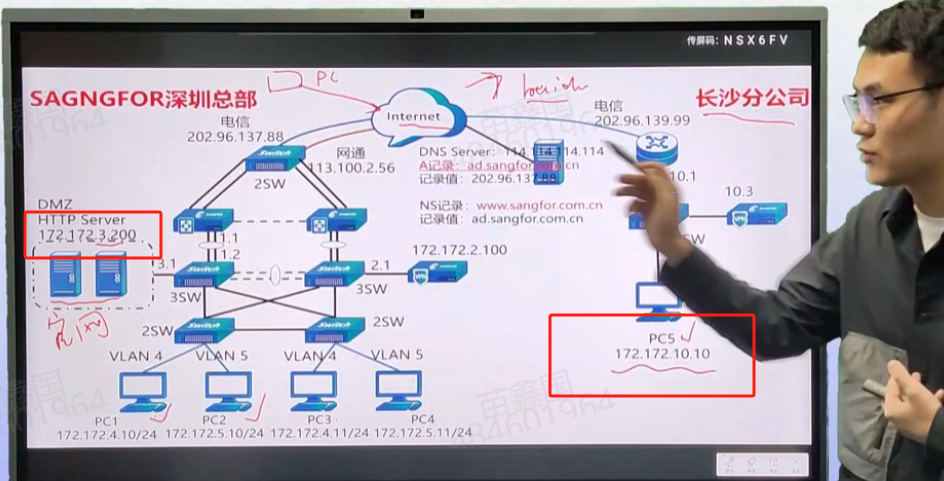
网络技术原理需要解决的5个问题
解决世界上任意两台设备时如何通讯的?? 第一个问题,pc1和pc3是怎么通讯的? 这俩属于同一个网段,那么同网段的是怎么通讯的? pc1和pc2属于不同的网段,第二个问题,不同网段的设备是…...
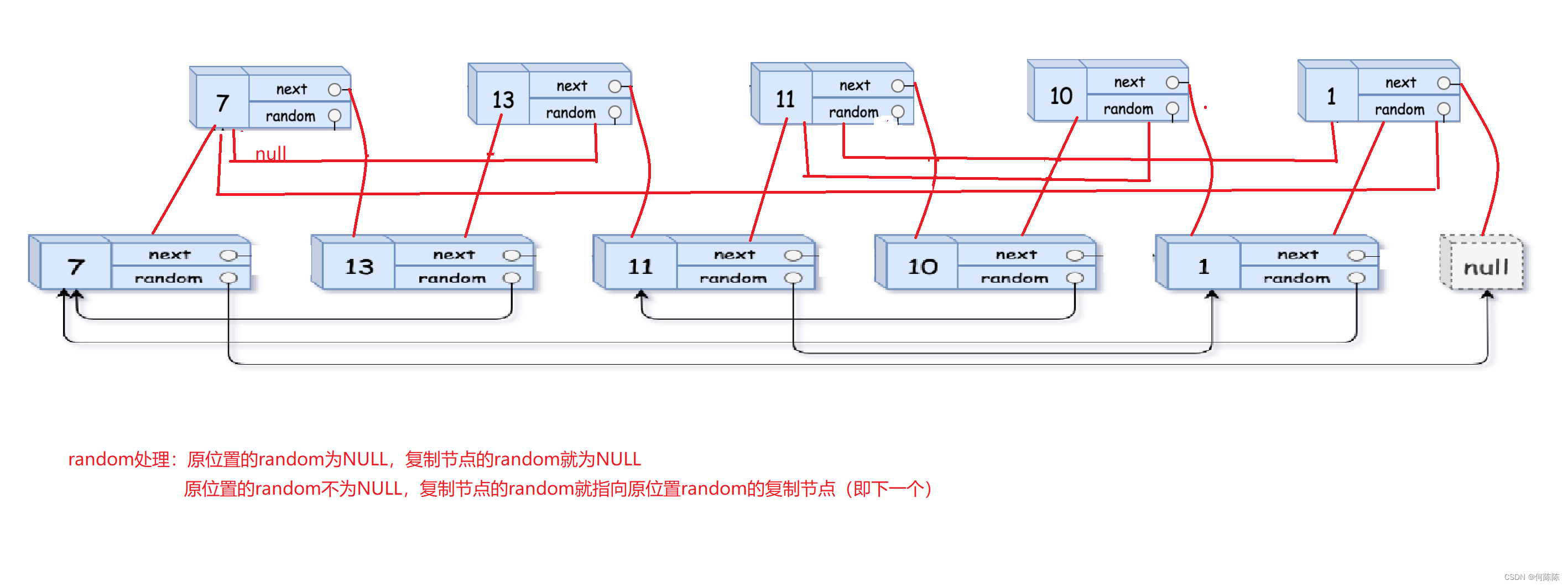
【数据结构】链表的大概认识及单链表的实现
目录 一、链表的概念及结构 二、链表的分类 三、单链表的实现 建立链表的节点: 尾插——尾删: 头插——头删: 查找: 指定位置之后删除——插入: 指定位置之前插入——删除指定位置: 销毁链表&am…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
HybridVLA——让单一LLM同时具备扩散和自回归动作预测能力:训练时既扩散也回归,但推理时则扩散
前言 如上一篇文章《dexcap升级版之DexWild》中的前言部分所说,在叠衣服的过程中,我会带着团队对比各种模型、方法、策略,毕竟针对各个场景始终寻找更优的解决方案,是我个人和我司「七月在线」的职责之一 且个人认为,…...

客户案例 | 短视频点播企业海外视频加速与成本优化:MediaPackage+Cloudfront 技术重构实践
01技术背景与业务挑战 某短视频点播企业深耕国内用户市场,但其后台应用系统部署于东南亚印尼 IDC 机房。 随着业务规模扩大,传统架构已较难满足当前企业发展的需求,企业面临着三重挑战: ① 业务:国内用户访问海外服…...

2025-05-08-deepseek本地化部署
title: 2025-05-08-deepseek 本地化部署 tags: 深度学习 程序开发 2025-05-08-deepseek 本地化部署 参考博客 本地部署 DeepSeek:小白也能轻松搞定! 如何给本地部署的 DeepSeek 投喂数据,让他更懂你 [实验目的]:理解系统架构与原…...
