DataStructure.时间和空间复杂度
时间和空间复杂度
- 【本节目标】
- 1. 如何衡量一个算法的好坏
- 2. 算法效率
- 3. 时间复杂度
- 3.1 时间复杂度的概念
- 3.2 大O的渐进表示法
- 3.3 推导大O阶方法
- 3.4 常见时间复杂度计算举例
- 3.4.1 示例1
- 3.4.2 示例2
- 3.4.3 示例3
- 3.4.4 示例4
- 3.4.5 示例5
- 3.4.6 示例6
- 3.4.7 示例7
- 4.空间复杂度
- 4.1 示例1
- 4.2 示例2
- 4.3 示例3
【本节目标】
- 算法效率
- 时间复杂度
- 空间复杂度
1. 如何衡量一个算法的好坏
下面求斐波那契数列的算法好还是不好,为什么?该如何衡量一个算法的好坏呢?
public static long Fib(int N) {if (N < 3) {return 1;}return Fib(N - 1) + Fib(N - 2);
}
2. 算法效率
算法效率分析主要分为两种,具体包括:
- 时间效率:也被称为时间复杂度。它主要衡量算法中基本操作的执行次数。在计算时间复杂度时,通常使用大O的渐进表示法。时间复杂度是评估算法运行速度快慢的重要指标,常见的时间复杂度包括O(1)、O(logn)、O(n)、O(n^2)等。随着问题规模的扩大,时间效率的重要性愈发突出,因为它直接影响到算法处理大数据集的能力。
- 空间效率:也被称为空间复杂度。它主要是对算法在运行中临时占用的空间大小的度量。换句话说,它计算了算法在运行过程中开辟了多少额外的空间,例如数组的大小。如果算法没有开辟新的数组,则其空间复杂度为O(1);若开辟了N个数组,则为O(N)。对于递归调用,空间复杂度取决于递归的深度或次数。虽然在现代计算机硬件环境中,内存空间越来越大,对空间效率的考虑可能相对较少,但优化空间使用仍然是一个好的编程实践,特别是在处理大规模数据或资源受限的环境中。
3. 时间复杂度
3.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个数学函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
3.2 大O的渐进表示法
// 请计算一下func1基本操作执行了多少次?
public static void func1(int N) {int count = 0;for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {count++;}}for (int k = 0; k < 2 * N; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);
}
Func1 执行的基本操作次数 :

- N = 10 F(N) = 130
- N = 100 F(N) = 10210
- N = 1000 F(N) = 1002010
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
3.3 推导大O阶方法
- 用常数1取代运行时间中的所有加法常数。
- 在修改后的运行次数函数中,只保留最高阶项。
- 如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:

- N = 10 F(N) = 100
- N = 100 F(N) = 10000
- N = 1000 F(N) = 1000000
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
3.4 常见时间复杂度计算举例
3.4.1 示例1
// 计算func2的时间复杂度?
void func2(int N) {int count = 0;for (int k = 0; k < 2 * N; k++) {count++;}int M = 10;while ((M--) > 0) {count++;}System.out.println(count);
}
首先,我们分析func2函数中的各个部分:
-
有一个
for循环,其循环次数为2 * N。在这个循环中,count每次递增1,因此这部分的时间复杂度是O(N)。 -
紧接着,有一个
while循环,其循环次数固定为10次(因为M被初始化为10,并且在每次循环中递减,直到为0)。在这部分,count也每次递增1,但这部分的时间复杂度是常数时间,即O(1),因为它不依赖于输入N。 -
最后,有一个输出语句
System.out.println(count);,这也是常数时间操作,即O(1)。
综上所述,虽然函数中有两个循环,但第二个循环的时间复杂度是常数,不随N的变化而变化。因此,整个函数func2的时间复杂度主要由第一个for循环决定,即O(N)。
所以,func2的时间复杂度是O(N)。
3.4.2 示例2
// 计算func3的时间复杂度?
void func3(int N, int M) {int count = 0;for (int k = 0; k < M; k++) {count++;}for (int k = 0; k < N; k++) {count++;}System.out.println(count);
}
在func3函数中,我们有两个for循环:
-
第一个
for循环的次数由参数M决定,循环体内执行的操作是count++,这是一个常数时间操作。因此,第一个循环的时间复杂度是O(M)。 -
第二个
for循环的次数由参数N决定,同样地,循环体内执行的操作也是count++,这也是一个常数时间操作。因此,第二个循环的时间复杂度是O(N)。 -
最后,有一个输出语句
System.out.println(count);,这是常数时间操作,即O(1)。
综合考虑两个循环,它们各自独立,且没有嵌套关系,所以整个函数的时间复杂度是两个循环时间复杂度的和,即O(M + N)。
因此,func3的时间复杂度是O(M + N)。这意味着函数执行所需的时间与M和N的线性之和成正比。
3.4.3 示例3
// 计算func4的时间复杂度?
void func4(int N) {int count = 0;for (int k = 0; k < 100; k++) {count++;}System.out.println(count);
}
在func4函数中,我们有一个for循环和一个输出语句:
-
for循环的次数是固定的,为100次,因为循环条件是k < 100。在循环体内,执行的操作是count++,这是一个常数时间操作。由于循环次数不依赖于输入N,因此这部分的时间复杂度是常数时间,即O(1)。这里需要注意的是,尽管循环执行了100次,但时间复杂度仍然看作是常数时间,因为无论N的值是多少,这个循环的次数都不会改变。 -
输出语句
System.out.println(count);也是常数时间操作,即O(1)。
综合考虑上述两部分,整个函数func4的时间复杂度是常数时间,即O(1)。这意味着无论输入N的大小如何,函数执行所需的时间都是固定的。
因此,func4的时间复杂度是O(1)。
3.4.4 示例4
// 计算bubbleSort的时间复杂度?
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}
}private void Swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}
冒泡排序(Bubble Sort)的时间复杂度分析如下:
在最坏的情况下,即数组完全逆序时,冒泡排序需要进行n-1轮比较和交换(n是数组的长度)。在每一轮中,冒泡排序会从数组的开始比较相邻的元素,并且根据需要交换它们,直到到达当前轮的结束位置。这个过程会重复进行,直到整个数组排序完成。
对于每一轮,我们需要进行end-1次比较(end是当前轮需要考虑的数组长度,它随着每一轮的递减而减少)。因此,如果我们计算所有轮中的比较次数,我们会发现它是一个等差数列的和,首项为n-1,末项为1,项数为n-1。等差数列的和公式为S = n/2 * (首项 + 末项) * 项数,代入得S = (n-1)/2 * (n-1 + 1) * (n-1) = (n-1)^2 * (n/2)。由于我们只关心最高次项来确定时间复杂度,因此可以简化为O(n^2)。
另外,考虑到最好情况下,即数组已经排好序时,冒泡排序可能在第一轮就终止,因为sorted标志会在第一轮后被设置为true,从而跳出外层循环。这种情况下,时间复杂度为O(n)。但是,由于我们通常在分析算法复杂度时考虑的是最坏情况,所以冒泡排序的时间复杂度通常被认为是O(n^2)。
综上所述,冒泡排序的时间复杂度是O(n^2)。
此外,值得注意的是,空间复杂度是O(1),因为冒泡排序是原地排序算法,不需要额外的存储空间。
Swap函数的时间复杂度是O(1),因为它只执行了固定数量的操作,不依赖于输入数组的大小。因此,在分析冒泡排序的整体时间复杂度时,Swap函数的开销可以被忽略。
3.4.5 示例5
// 计算binarySearch的时间复杂度?
int binarySearch(int[] array, int value) {int begin = 0;int end = array.length - 1;while (begin <= end) {int mid = begin + ((end - begin) / 2);if (array[mid] < value)begin = mid + 1;else if (array[mid] > value)end = mid - 1;elsereturn mid;}return -1;
}
二分查找(Binary Search)算法的时间复杂度分析如下:
二分查找是一种在有序数组中查找特定元素的算法。在每次迭代中,算法都会将搜索范围减半,通过比较中间元素与目标值来决定接下来在数组的哪一半中继续搜索。
在最坏的情况下,即目标值不存在于数组中或者存在于数组的最末端,二分查找需要进行log2(n)次迭代(这里的n是数组的长度)。这是因为每次迭代都会将搜索范围减半,所以需要迭代的次数与数组的长度成对数关系。
因此,二分查找的时间复杂度是O(log n),这里的n代表数组的长度。这意味着,无论数组有多大,二分查找所需的迭代次数都相对较少,使得它成为一种非常高效的查找算法,尤其是在处理大规模数据集时。
综上所述,binarySearch函数的时间复杂度是O(log n)。这里的log是以2为底的对数,但在复杂度分析中,我们通常省略底数,因为对于不同的底数,复杂度仍然是相同的数量级。
另外,值得注意的是,二分查找的空间复杂度是O(1),因为它只需要常数级别的额外空间来存储begin、end和mid等变量。
3.4.6 示例6
// 计算阶乘递归factorial的时间复杂度?
long factorial(int N) {return N < 2 ? N : factorial(N - 1) * N;
}
阶乘递归函数 factorial 的时间复杂度分析如下:
递归函数的时间复杂度通常通过分析递归树或递归调用的次数来确定。在这个阶乘函数中,每次递归调用都会使 N 减少 1,直到 N 变为 1 或 0。因此,递归的深度(即递归调用的次数)与输入 N 成正比。
对于给定的输入 N,函数会进行 N 次递归调用(包括初始调用)。在每次递归调用中,除了递归调用自身外,还执行了一次乘法操作。由于乘法操作的时间复杂度是常数时间 O(1),因此总的时间复杂度主要取决于递归调用的次数。
所以,阶乘递归函数 factorial 的时间复杂度是 O(N),其中 N 是输入参数。这意味着函数执行所需的时间与 N 成线性关系。
另外,值得注意的是,虽然这个函数的时间复杂度是线性的,但当 N 很大时,递归可能会导致栈溢出或超出 long 类型的最大值。因此,在实际应用中,可能需要考虑使用迭代版本的阶乘函数或者使用大数库来处理大数阶乘。
3.4.7 示例7
// 计算斐波那契递归fibonacci的时间复杂度?
int fibonacci(int N) {return N < 2 ? N : fibonacci(N - 1) + fibonacci(N - 2);
}
斐波那契递归函数 fibonacci 的时间复杂度分析稍微复杂一些,因为它涉及到大量的重复计算。我们来详细分析一下:
这个函数使用递归方式计算斐波那契数列的第 N 项,其中 N 是输入参数。斐波那契数列是这样一个序列:0, 1, 1, 2, 3, 5, 8, 13, …,其中每个数是前两个数的和。
在递归函数中,为了计算 fibonacci(N),需要计算 fibonacci(N-1) 和 fibonacci(N-2)。然而,这两个递归调用又会进一步引发更多的递归调用,而且很多计算是重复的。例如,在计算 fibonacci(N) 时会计算 fibonacci(N-1),而在计算 fibonacci(N-1) 时又会再次计算 fibonacci(N-2),这个 fibonacci(N-2) 在计算 fibonacci(N) 时已经被计算过一次了。
这种重复计算会导致函数的时间复杂度非常高。实际上,这个递归函数的时间复杂度是指数级的,具体来说是 O(2^N),其中 N 是输入参数。这是因为对于每个 N,都会有两个递归调用,形成一个二叉树结构的调用图,其深度为 N,每一层的节点数大致是上一层的两倍。
因此,尽管斐波那契递归函数在概念上很简单,但由于大量的重复计算,它的性能非常差。在实际应用中,通常会使用动态规划、迭代或其他优化方法来避免这种重复计算,从而降低时间复杂度。例如,可以使用一个数组来存储已经计算过的斐波那契数,以便在需要时重用这些值,而不是重新计算它们。这种方法可以将时间复杂度降低到 O(N)。
4.空间复杂度
4.1 示例1
// 计算bubbleSort的间空复杂度?
void bubbleSort(int[] array) {for (int end = array.length; end > 0; end--) {boolean sorted = true;for (int i = 1; i < end; i++) {if (array[i - 1] > array[i]) {Swap(array, i - 1, i);sorted = false;}}if (sorted == true) {break;}}
}private void Swap(int[] array, int i, int j) {int tmp = array[i];array[i] = array[j];array[j] = tmp;
}
冒泡排序(Bubble Sort)算法的空间复杂度分析如下:
空间复杂度是指算法在运行过程中临时占用存储空间的大小。在冒泡排序算法中,我们主要关注两个方面:存储输入数组的空间和算法运行过程中额外使用的空间。
-
存储输入数组的空间:这部分空间是固定的,由输入数组的大小决定,与算法本身无关。因此,在分析算法的空间复杂度时,我们通常不考虑这部分空间。
-
算法运行过程中额外使用的空间:在冒泡排序中,除了输入数组外,我们只需要一些额外的变量来辅助排序过程。在你的代码中,这些变量包括
end、sorted、i以及Swap函数中的tmp。这些都是简单的整型变量或布尔变量,它们占用的空间是常数级别的,与输入数组的大小无关。
综上所述,冒泡排序算法的空间复杂度是O(1)。这是因为算法在运行过程中只需要常数级别的额外空间,不随输入数组的大小而变化。这意味着,无论输入数组有多大,冒泡排序所需的额外空间都是固定的。
4.2 示例2
// 计算斐波那契递归fibonacci的空间复杂度?
int fibonacci(int N) {return N < 2 ? N : fibonacci(N - 1) + fibonacci(N - 2);
}
斐波那契递归函数 fibonacci 的空间复杂度主要由递归调用的深度决定。由于该函数采用递归方式计算斐波那契数列,每次递归调用都会将当前函数的执行上下文压入系统栈,直到递归到达基准情况(N < 2)时开始返回。
在最坏的情况下,即计算 fibonacci(N) 时,递归调用的深度将与 N 成正比。这是因为每个递归调用都会进一步调用 fibonacci(N-1) 和 fibonacci(N-2),形成了一棵二叉递归树。尽管存在大量的重复计算,但从空间占用的角度来看,我们关心的是递归树的最大深度。
递归树的最大深度大致为 N,因为每次递归调用都会使 N 减小 1 或 2,直到 N 变为 0 或 1。因此,系统栈中需要存储的递归调用上下文数量最多为 N 个。
所以,斐波那契递归函数 fibonacci 的空间复杂度是 O(N),其中 N 是输入参数。这意味着函数执行所需的最大栈空间与 N 成线性关系。在实际应用中,由于递归调用的数量巨大,这个函数很容易导致栈溢出,特别是对于较大的 N 值。因此,虽然从理论上看空间复杂度是线性的,但在实践中这个函数可能会因为栈空间不足而失败。
4.3 示例3
// 计算阶乘递归factorial的空间复杂度?
long factorial(int N) {return N < 2 ? N : factorial(N - 1) * N;
}
阶乘递归函数 factorial 的空间复杂度分析如下:
该函数是一个递归函数,用于计算给定整数 N 的阶乘。在递归过程中,每次函数调用都会创建一个新的执行上下文,该上下文需要被存储在系统栈中,直到函数返回结果。
对于 factorial 函数,每次递归调用都会使 N 减 1,直到达到基准情况 N < 2。因此,递归的深度(也就是递归调用的次数)与 N 的值直接相关。
在最坏的情况下,即当 N 是一个较大的正整数时,递归调用的次数将是 N 次(如果我们从 N 开始计数,直到递归到基准情况)。每次递归调用都会在系统栈中增加一个执行上下文,因此栈的最大深度将是 N。
所以,阶乘递归函数 factorial 的空间复杂度是 O(N),其中 N 是输入参数。这意味着函数执行所需的最大栈空间与 N 成线性关系。尽管每次递归调用本身不占用太多额外空间(除了系统栈中的执行上下文外),但由于递归的深度可能很大,因此该函数在处理非常大的 N 值时可能会遇到栈溢出的问题。
相关文章:

DataStructure.时间和空间复杂度
时间和空间复杂度 【本节目标】1. 如何衡量一个算法的好坏2. 算法效率3. 时间复杂度3.1 时间复杂度的概念3.2 大O的渐进表示法3.3 推导大O阶方法3.4 常见时间复杂度计算举例3.4.1 示例13.4.2 示例23.4.3 示例33.4.4 示例43.4.5 示例53.4.6 示例63.4.7 示例7 4.空间复杂度4.1 示…...

[Spring Boot]Netty-UDP客户端
文章目录 简述Netty-UDP集成pom引入ClientHandler调用 消息发送与接收在线UDP服务系统调用 简述 最近在一些场景中需要使用UDP客户端进行,所以开始集成新的东西。本文集成了一个基于netty的SpringBoot的简单的应用场景。 Netty-UDP集成 pom引入 <!-- netty --…...

基础C语言知识串串香11☞宏定义与预处理、函数和函数库
六、C语言宏定义与预处理、函数和函数库 6.1 编译工具链 源码.c ——> (预处理)——>预处理过的.i文件——>(编译)——>汇编文件.S——>(汇编)——>目标文件.o->(链接)——>elf可执行程序 预处理用预处理器,编译用编译器,…...

Python 3 函数
Python 3 函数 引言 Python 是一种高级编程语言,以其简洁明了的语法和强大的功能而闻名。在 Python 中,函数是一等公民,扮演着至关重要的角色。它们是组织代码、提高代码复用性和模块化编程的关键。本文将深入探讨 Python 3 中的函数,包括其定义、特性、类型以及最佳实践…...

【Linux详解】冯诺依曼架构 | 操作系统设计 | 斯坦福经典项目Pintos
目录 一. 冯诺依曼体系结构 (Von Neumann Architecture) 注意事项 存储器的意义:缓冲 数据流动示例 二. 操作系统 (Operating System) 操作系统的概念 操作系统的定位与目的 操作系统的管理 系统调用和库函数 操作系统的管理: sum 三. 系统调…...
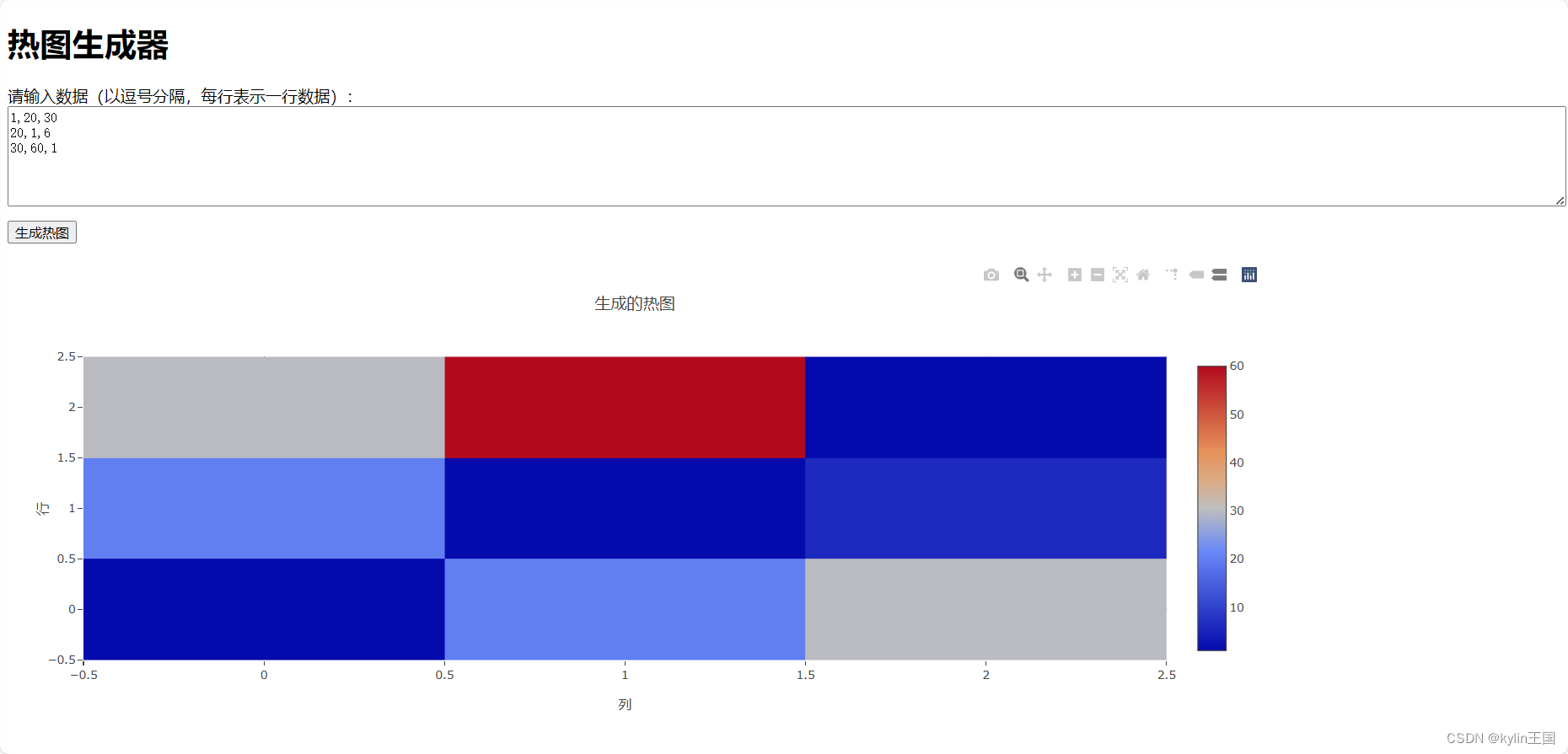
html做一个画热图的软件
完整示例 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><title>热图生成器</title><script src"https://cdn.plot.ly/plotly-latest.min.js"></script><style>body …...
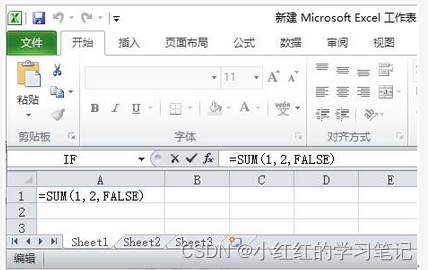
软考初级网络管理员__软件单选题
1.在Excel 中,设单元格F1的值为56.323,若在单元格F2中输入公式"TEXT(F1,"¥0.00”)”,则单元格F2的值为()。 ¥56 ¥56.323 ¥56.32 ¥56.00 2.要使Word 能自动提醒英文单…...

数据库新技术【分布式数据库】
文章目录 第一章 概述1.1 基本概念1.1.1 分布式数据库1.1.2 数据管理的透明性1.1.3 可靠性1.1.4 分布式数据库与集中式数据库的区别 1.2 体系结构1.3 全局目录1.4 关系代数1.4.1 基操1.4.2 关系表达式1.4.3 查询树 第二章 分布式数据库的设计2.1 设计策略2.2 分布设计的目标2.3…...

关于运用人工智能帮助自己实现英语能力的有效提升?
# 实验报告 ## 实验目的 - 描述实验的目标:自己可以知道,自己的ai学习方法是否可以有效帮助自己实现自己的学习提升。 预期结果:在自己利用科技对于自己进行学习的过程中,自己的成长速度应该是一个幂指数的增长 ## 文献回顾 根据…...

IPv6知识点整理
IPv6:是英文“Internet Protocol Version 6”(互联网协议第6版)的缩写,是互联网工程任务组(IETF)设计的用于替代IPv4的下一代IP协议,其地址数量号称可以为全世界的每一粒沙子编上一个地址 。 国…...
——体系:数据标准化——概述、关注焦点)
数据赋能(127)——体系:数据标准化——概述、关注焦点
概述 数据标准化是指将数据按照一定的规范和标准进行处理的过程。 数据标准化是属于数据整理过程。 数据标准化的目的在于提高数据的质量、促进数据的共享和交互、降低数据管理的成本,并增强数据的安全性。通过数据标准化,可以使得数据具有统一的格式…...

【 ARMv8/ARMv9 硬件加速系列 3.5.1 -- SVE 谓词寄存器有多少位?】
文章目录 SVE 谓词寄存器(predicate registers)简介SVE 谓词寄存器的位数SVE 谓词寄存器对向量寄存器的控制SVE 谓词寄存器位数计算SVE 谓词寄存器小结 SVE 谓词寄存器(predicate registers)简介 ARMv9的Scalable Vector Extension (SVE) 引入了谓词寄存器(Predica…...

Python - 调用函数时检查参数的类型是否合规
前言 阅读本文大概需要3分钟 说明 在python中,即使加入了类型注解,使用注解之外的类型也是不报错的 def test(uid: int):print(uid)test("999")但是我就想要类型不对就直接报错确实可以另辟蹊径,实现报错,似乎有强…...

Python基础面试题解答
Python基础面试题解答 基础语法 1. Python中的变量是如何管理内存的? Python中的变量通过引用计数来管理内存。当一个变量被创建时,会分配一个内存地址,并记录引用次数。当引用次数变为0时,垃圾回收机制会自动释放该内存。 2.…...
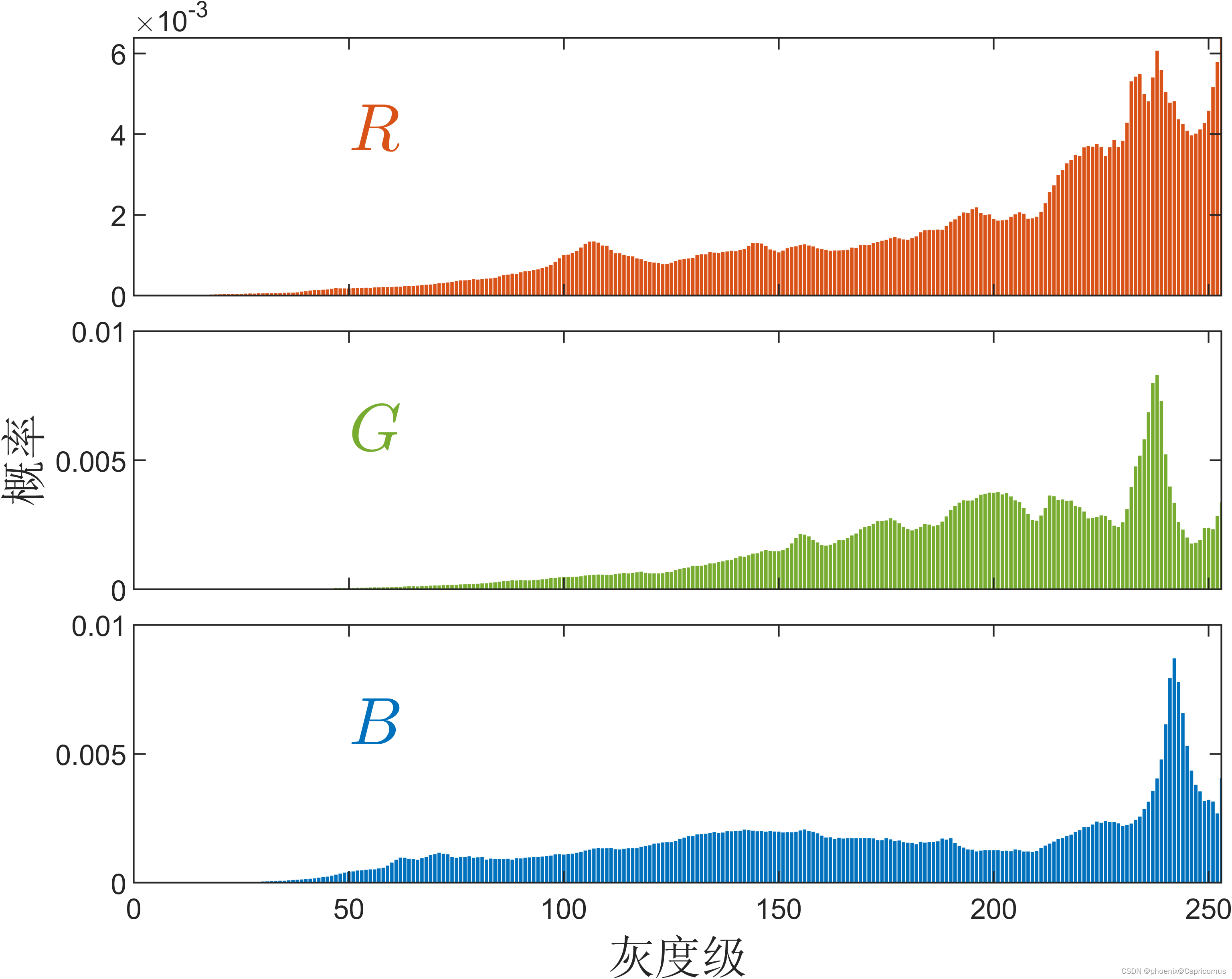
MATLAB直方图中bin中心与bin边界之间的转换
要将 bin 中心转换为 bin 边界,请计算 centers 中各连续值之间的中点。 d diff(centers)/2; edges [centers(1)-d(1), centers(1:end-1)d, centers(end)d(end)];要将 bin 边界转换为bin 中心 bincenters binedges(1:end-1)diff(binedges)/2;...
Chromium 开发指南2024 Mac篇-开始编译Chromium(五)
1.引言 在之前的指南中,我们已经详细介绍了在 macOS 上编译和开发 Chromium 的准备工作。您学会了如何安装和配置 Xcode,如何下载和配置 depot_tools,以及如何获取 Chromium 的源代码。通过这些步骤,您的开发环境已经搭建完毕&am…...

2024.06.11校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、校招 | 美团2025届北斗计划正式启动(内推) 校招 | 美团2025届北斗计划正式启动(内推) 2、实习 | 沃尔沃汽车 Open Day & 实习招聘 …...

linux 免密备份文件到另外一台服务器
简单说,A服务器备份到B服务器。就是将A服务器的文件复制传输到B服务器进行备份。这种场景可以应用到简单的定时器自动备份数据文件。 具体步骤: 1、A服务器上执行以下命令并一直按回车键,然后在/root/.ssh目录中可以看到私钥和公钥。其中id…...
【html】用html写一个博物馆首页
效果图: 二级导航: 源码: <!DOCTYPE html> <html lang"zh"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><l…...
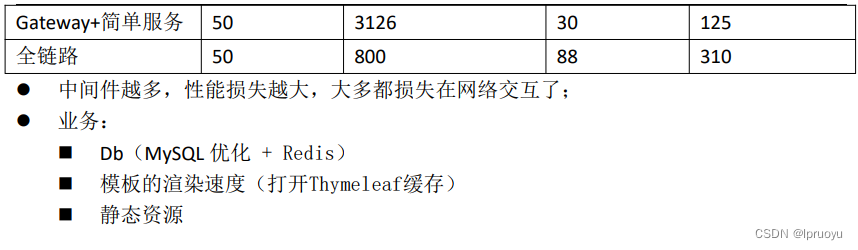
【雷丰阳-谷粒商城 】【分布式高级篇-微服务架构篇】【13】压力压测JMeter-性能监控jvisualvm
持续学习&持续更新中… 守破离 【雷丰阳-谷粒商城 】【分布式高级篇-微服务架构篇】【13】压力压测JMeter-性能监控jvisualvm 压力测试概述性能指标 JMeter基本使用添加线程组添加 HTTP 请求添加监听器启动压测&查看分析结果JMeter Address Already in use 错误解决 性…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...
