RSA密码系统的特定密钥泄露攻击与Coppersmith方法的应用
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。
RSA密码系统作为当前最广泛使用的公钥加密算法之一,其安全性依赖于大整数分解问题的困难性。然而,随着计算能力的提高和算法优化,特别是Coppersmith方法的出现,使得在特定条件下对RSA系统进行密钥恢复成为可能。本文将深入探讨Coppersmith方法的原理,以及如何应用于针对RSA的特定密钥泄露攻击。
1. RSA密码系统基础
RSA算法基于一个简单的数论事实:对于大的合数 n n n,其因数分解是计算上不可行的。RSA的安全性依赖于以下两个假设:一是大整数的因数分解问题(CIFP)是困难的;二是计算离散对数问题(CDLP)在模 n n n 下也是困难的。
1.1 RSA算法概述
RSA算法的基本流程包括密钥生成、加密和解密三个过程。其数学基础主要依赖于欧拉定理和模幂运算。通过合理选择密钥参数,可以保证加密和解密过程的正确性和安全性。
1.2 数论基础
RSA算法依赖于数论中的几个基本概念:
- 素数:只有1和其自身两个因子的正整数。
- 模运算:给定两个整数 a a a 和 n n n,模运算表示 a a a 除以 n n n 的余数。
- 欧拉函数:对于一个正整数 n n n,欧拉函数 𝜙( n n n)表示小于 n n n 且与 n n n 互质的正整数个数。
2. RSA的密钥生成过程
RSA密钥生成包括以下步骤:
- 随机选择两个大素数 p p p 和 q q q。
- 计算 n n n= p q pq pq,其中 n n n 是公钥和私钥的模数。
- 计算 𝜙( n n n) = ( p p p−1)( q q q−1),欧拉函数值。
- 选择一个整数 e e e,使得 1< e e e<𝜙( n n n),且 gcd( e e e,𝜙( n n n))=1,作为公钥指数。
- 计算 d d d,使得 d e de de ≡ 1 mod 𝜙( n n n),作为私钥指数。
2.1 公钥与私钥
公钥由 ( n , e ) (n,e) (n,e) 组成,用于加密数据;私钥由 ( n , d ) (n,d) (n,d) 组成,用于解密数据。安全性依赖于 n n n 的因数分解难度以及私钥 d d d 的保密性。
2.2 密钥选择的安全性
选择大素数 p p p 和 q q q 是关键,过小的素数容易被因数分解,从而破解整个RSA系统。此外,选择的 e e e 和 d d d 也需满足特定条件,以确保加密和解密过程的正确性。
3. Coppersmith方法原理
Coppersmith方法是一种解决模 N N N 下多项式方程近似根的方法。对于多项式 f ( x ) f(x) f(x),如果存在一个解 x x x,使得 ∣ f f f( x x x)∣< N 1 / k N^{1/k} N1/k,其中 k k k 是多项式的度数,那么Coppersmith方法可以在多项式时间内找到这样的解。
3.1 Coppersmith方法简介
Coppersmith方法基于Lattice reduction(格约简)和LLL算法(Lenstra–Lenstra–Lovász)的结合,用于找到模数下的小根。其核心思想是将求解模多项式方程的问题转化为一个格中的短向量问题。
3.2 LLL算法
LLL算法是一种用于格约简的多项式时间算法。它可以在格中找到一个近似的最短向量,从而解决一些在数论和密码学中的重要问题。
3.3 应用场景
Coppersmith方法可以应用于以下场景:
- 小公开指数攻击:当公钥指数 e e e 较小时,可以利用该方法求解相应的方程。
- 低位泄露攻击:当密钥的低位部分泄露时,可以通过构建相应的多项式方程来恢复整个密钥。
4. RSA特定密钥泄露攻击
4.1 攻击背景
在实际应用中,RSA密钥可能因为某些原因部分泄露,例如私钥指数 d d d 的部分位或者加密后的密文的一部分。这种情况下,攻击者可以利用Coppersmith方法尝试恢复完整的密钥。
4.2 攻击模型
假设攻击者已知私钥指数 d d d 的低位 d L d_{L} dL,可以构建如下多项式:
f ( x ) = x e − m m o d n f(x) = x^e - m \mod n f(x)=xe−mmodn
其中, m m m 是已知的密文, e e e 是公钥指数。
4.3 应用Coppersmith方法
利用Coppersmith方法,攻击者可以找到满足以下条件的 x x x:
∣ f ( x ) ∣ < n 1 / k |f(x)| < n^{1/k} ∣f(x)∣<n1/k
如果 x x x 的值能够被确定,那么可以通过 x e m o d n = m x^e \mod n = m xemodn=m 来解密密文。
4.4 具体步骤
- 信息收集:获取泄露的密钥信息,如私钥指数的低位 d L d_L dL。
- 多项式构建:基于已知信息构建多项式 f ( x ) f(x) f(x)。
- 格构造:根据Coppersmith方法,构造对应的格。
- 应用LLL算法:利用LLL算法对格进行约简,找到短向量。
- 解方程:通过解短向量对应的多项式方程,找到近似根,从而恢复密钥。
5. 攻击流程图
6. RSA安全性分析
6.1 增强密钥安全性
Coppersmith方法的应用表明,即使只有部分密钥信息泄露,也可能对RSA系统的安全性构成威胁。为了增强RSA系统的安全性,可以采取以下措施:
- 增加密钥长度:使用更大的素数 p p p 和 q q q,增加 n n n 的位数,提高因数分解的难度。
- 选择合适的公钥指数:避免使用过小的公钥指数 e e e,选择较大的 e e e 以提高安全性。
- 保护私钥:加强私钥的存储和管理,避免泄露。
6.2 后量子密码学
随着量子计算的发展,传统的RSA系统面临更大的安全威胁。后量子密码学旨在开发对量子计算机攻击具有抗性的加密算法,以确保未来的信息安全。
6.3 安全参数选择
选择适当的安全参数对于RSA系统的安全性至关重要。需要根据当前的计算能力和已知攻击方法,调整密钥长度和算法参数,以确保系统的安全性。
Coppersmith方法为密码学研究提供了一种新的视角,尤其是在处理模多项式方程时。尽管它为攻击者提供了一种可能的攻击手段,但也促进了密码学界对现有加密算法的安全性进行更深入的分析和改进。
在实际应用中,建议定期更新加密系统,采用最新的安全标准和算法,确保数据和通信的安全性。同时,密钥管理和信息保护也需要得到足够的重视,以防止由于密钥泄露而导致的安全问题。
通过对Coppersmith方法及其在RSA特定密钥泄露攻击中的应用的深入分析,可以更好地理解RSA系统的潜在风险,并采取相应的措施进行防范,保障信息安全。
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。
相关文章:

RSA密码系统的特定密钥泄露攻击与Coppersmith方法的应用
PrimiHub一款由密码学专家团队打造的开源隐私计算平台,专注于分享数据安全、密码学、联邦学习、同态加密等隐私计算领域的技术和内容。 RSA密码系统作为当前最广泛使用的公钥加密算法之一,其安全性依赖于大整数分解问题的困难性。然而,随着计…...

从零开始精通Onvif之音视频流传输
💡 如果想阅读最新的文章,或者有技术问题需要交流和沟通,可搜索并关注微信公众号“希望睿智”。 概述 Onvif协议的核心作用之一,是定义了如何通过网络访问和控制IP摄像机和其他视频设备。Onvif协议不仅涉及设备发现、设备管理&…...

CentOS 7、Debian、Ubuntu,这些是什么意思
CentOS 7、Debian、Ubuntu 都是基于 Linux 内核的操作系统,它们各自有不同的特性和用途。以下是对它们的详细解释: CentOS 7 CentOS(Community ENTerprise Operating System) 是一个基于开源的 Linux 发行版。CentOS 7 是 CentOS …...

安装Flask
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 大多数Python包都使用pip实用工具安装,使用Virtualenv创建虚拟环境时会自动安装pip。激活虚拟环境后,pip 所在的路径会被添加…...

OSPF开销、协议优先级、定时器(华为)
#交换设备 OSPF开销值 如果没有定义OSPF接口的开销值,OSPF会根据该接口的带宽自动计算其开销值。 计算公式: 接口开销 带宽参考值 / 接口带宽 (取整数部分,结果小于1时取1)通过改变带宽参考值可以间接改变接口的开…...

接口与实现-常用实用类-Java
接口与实现 接口 使用关键字interface来定义一个接口,接口的定义分为接口声明和接口体,例如: interface Com{ ....... } 接口声明 interface 接口的名字 接口体 接口体中的抽象方法和常量 接口体中所有抽象方法的访问权限一定都是pu…...

【CSS in Depth 2 精译】1.5 渐进式增强
文章目录 1.5 渐进式增强1.5.1 利用层叠规则实现渐进式增强1.5.2 渐进式增强的选择器1.5.3 利用 supports() 实现特性查询启用浏览器实验特性 1.5 渐进式增强 要用好 CSS 这样一门不断发展演进中的语言,其中一个重要的因素就是要与时俱进,及时了解哪些功…...

k8s集群master故障恢复笔记
剔除故障节点 kubectl drain master故障节点 kubectl delete node master故障节点 kubeadm reset rm -rf /etc/kubernetes/manifests mkdir -p /etc/kubernetes/pki/etcd/ 从master其他节点拷 scp /etc/kubernetes/pki/ca.crt ca.key sa.key sa.pub front-proxy-ca.crt …...
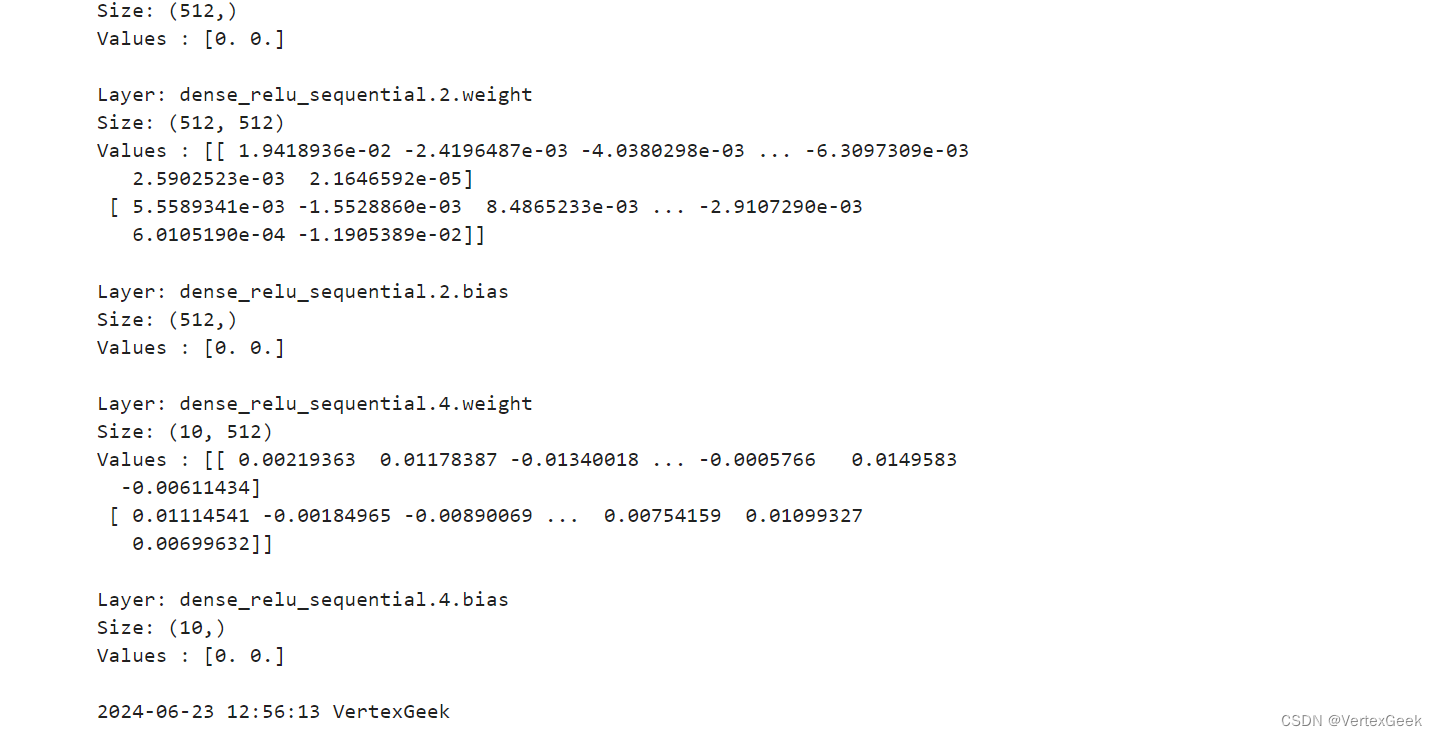
昇思25天学习打卡营第5天|网络构建
一、简介: 神经网络模型是由神经网络层和Tensor操作构成的,mindspore.nn提供了常见神经网络层的实现,在MindSpore中,Cell类是构建所有网络的基类(这个类和pytorch中的modul类是一样的作用),也是…...

Python开发日记--手撸加解密小工具(2)
目录 1. UI设计和代码生成 2.运行代码查看效果 3.小结 1. UI设计和代码生成 昨天讨论到每一类算法设计为一个Tab,利用的是TabWidget,那么接下来就要在每个Tab里设计算法必要的参数了,这里我们会用到组件有Label、PushButton、TextEdit、Ra…...

一文看懂TON链
一、背景与起源 The Open Network (TON) 的故事起始于2018年,当时全球知名的即时通讯软件Telegram计划推出自己的区块链平台及加密货币Gram,旨在构建一个既安全又高速的分布式网络,用以支持下一代去中心化应用程序(DApps)和数字资产。然而&a…...

(南京观海微电子)——TFT LCD压合技术
TFT-LCD TFT-LCD open cell后段制程主要指的是将驱动IC和PCB压合至液晶板上,这个制程主要由三个步骤组成: 1.ACF (Anisotropic Conductive Film)的涂布。 在液晶板需要压合驱动IC的地方涂布ACF,ACF又称异方性导电胶膜,特点是上下…...
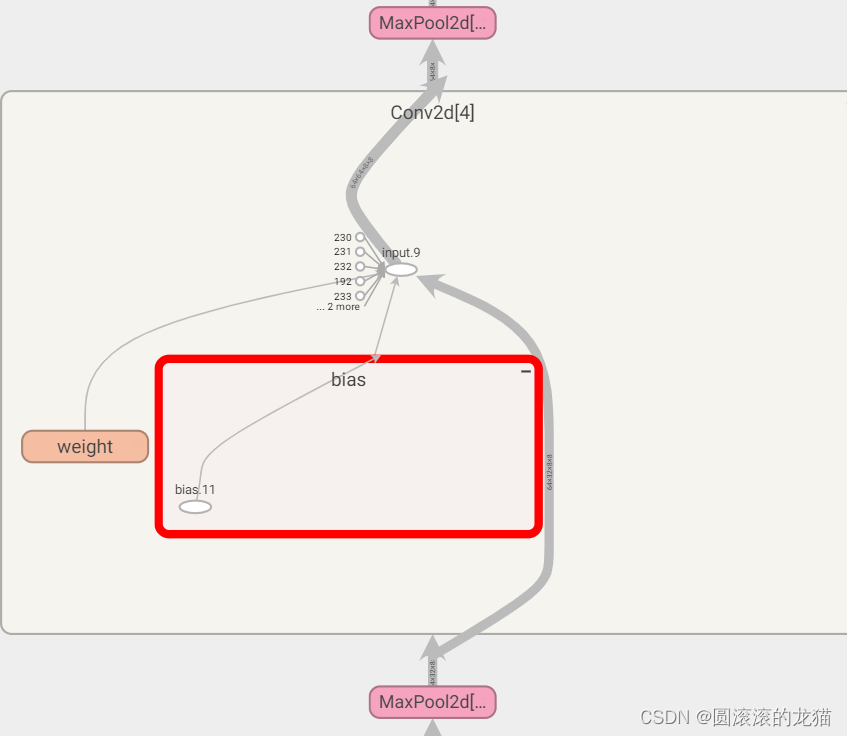
神经网络实战1-Sequential
链接:https://pytorch.org/docs/1.8.1/generated/torch.nn.Sequential.html#torch.nn.Sequential 完成这样一个网络模型 第一步新建一个卷积层 self.conv1Conv2d(3,32,5)#第一步将33232输出为32通道,卷积核5*5 注意一下:输出通道数等于卷积…...

Java中如何优化数据库查询性能?
Java中如何优化数据库查询性能? 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将深入探讨在Java中如何优化数据库查询性能,这是…...

从0开发一个Chrome插件:用户反馈与更新 Chrome 插件
前言 这是《从0开发一个Chrome插件》系列的第二十二篇文章,也是最终篇,本系列教你如何从0去开发一个Chrome插件,每篇文章都会好好打磨,写清楚我在开发过程遇到的问题,还有开发经验和技巧。 专栏: 从0开发一个Chrome插件:什么是Chrome插件?从0开发一个Chrome插件:开发…...

Failed to establish a new connection: [WinError 10061] 由于目标计算机积极拒绝,无法连接
在进行参数化读取时发现一个问题: 发现问题: requests.exceptions.ConnectionError: HTTPConnectionPool(hostlocalhost, port8081): Max retries exceeded with url: /jwshoplogin/user/update_information.do (Caused by NewConnectionError(<url…...
基于Java作业管理系统设计和实现(源码+LW+调试文档+讲解等)
💗博主介绍:✌全网粉丝10W,CSDN作者、博客专家、全栈领域优质创作者,博客之星、平台优质作者、专注于Java、小程序技术领域和毕业项目实战✌💗 🌟文末获取源码数据库🌟 感兴趣的可以先收藏起来,…...
)
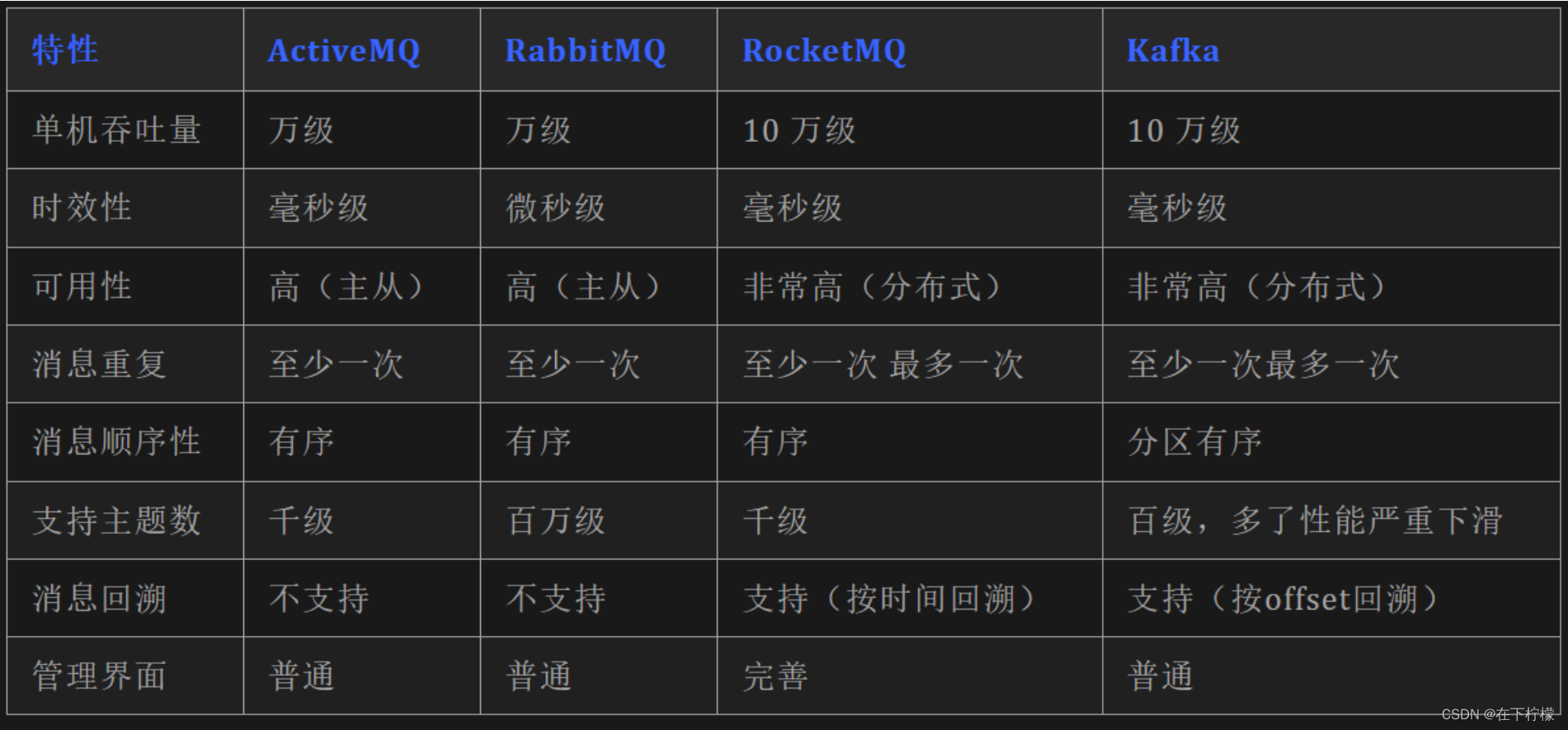
使用Kafka框架发送和接收消息(Java示例)
Kafka是一个开源的分布式流处理平台,以其在大数据和实时处理领域的广泛应用而闻名。以下是Kafka的关键特性以及它在消息传输方面的优势: 高吞吐量与低延迟:Kafka能够每秒处理数百万条消息,具有极低的延迟,这使得它非常…...
高可用电商支付架构设计方案
高可用电商支付架构设计 在现代电商业务中,支付过程是其中至关重要的一环,一个高可用、安全稳定的支付架构不仅可以提高整个系统的可靠性和扩展性,降低维护成本,还可以优化用户体验,增加用户黏性。 本文将提出一种高…...
PriorityQueue详解(含动画演示)
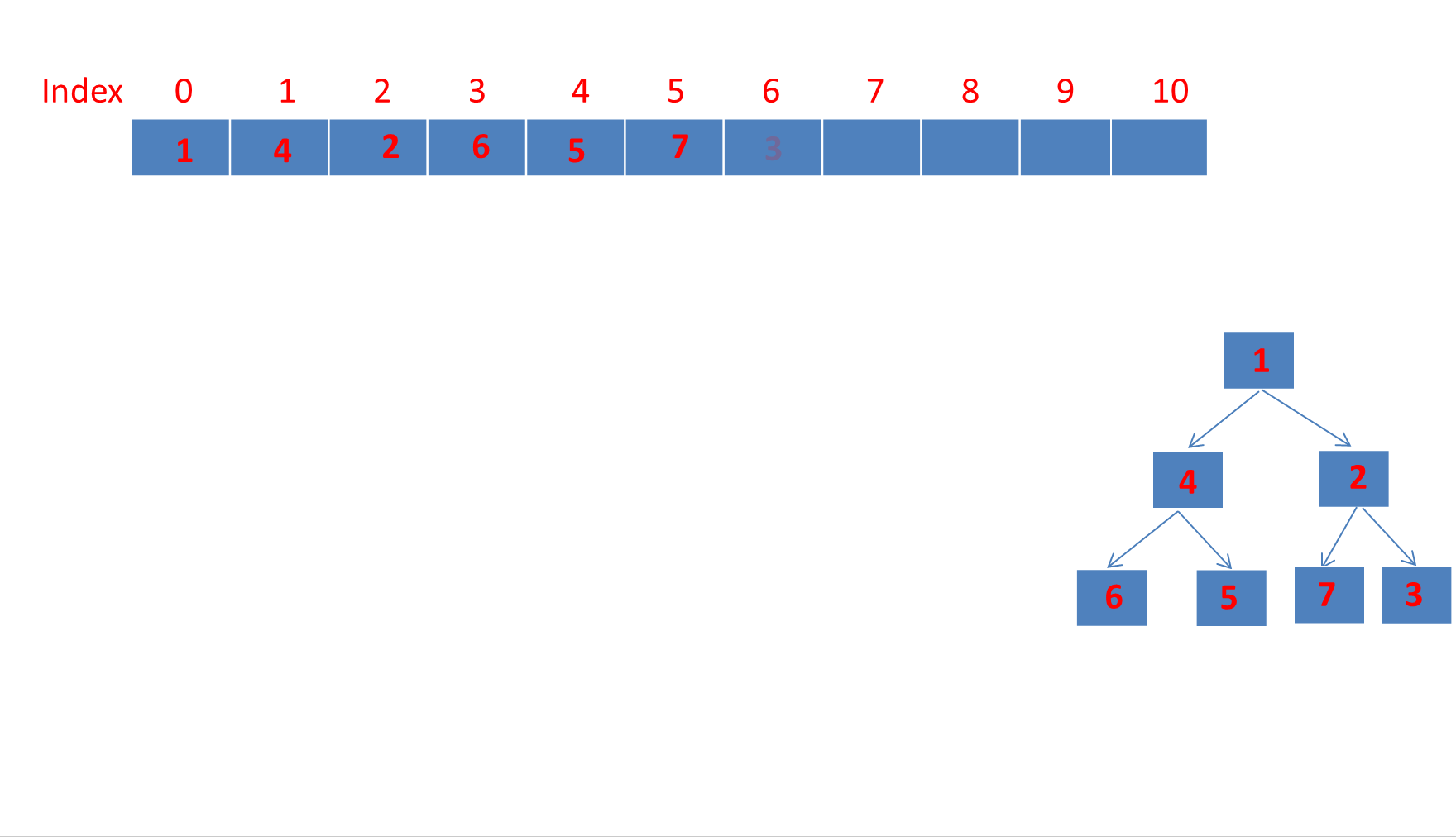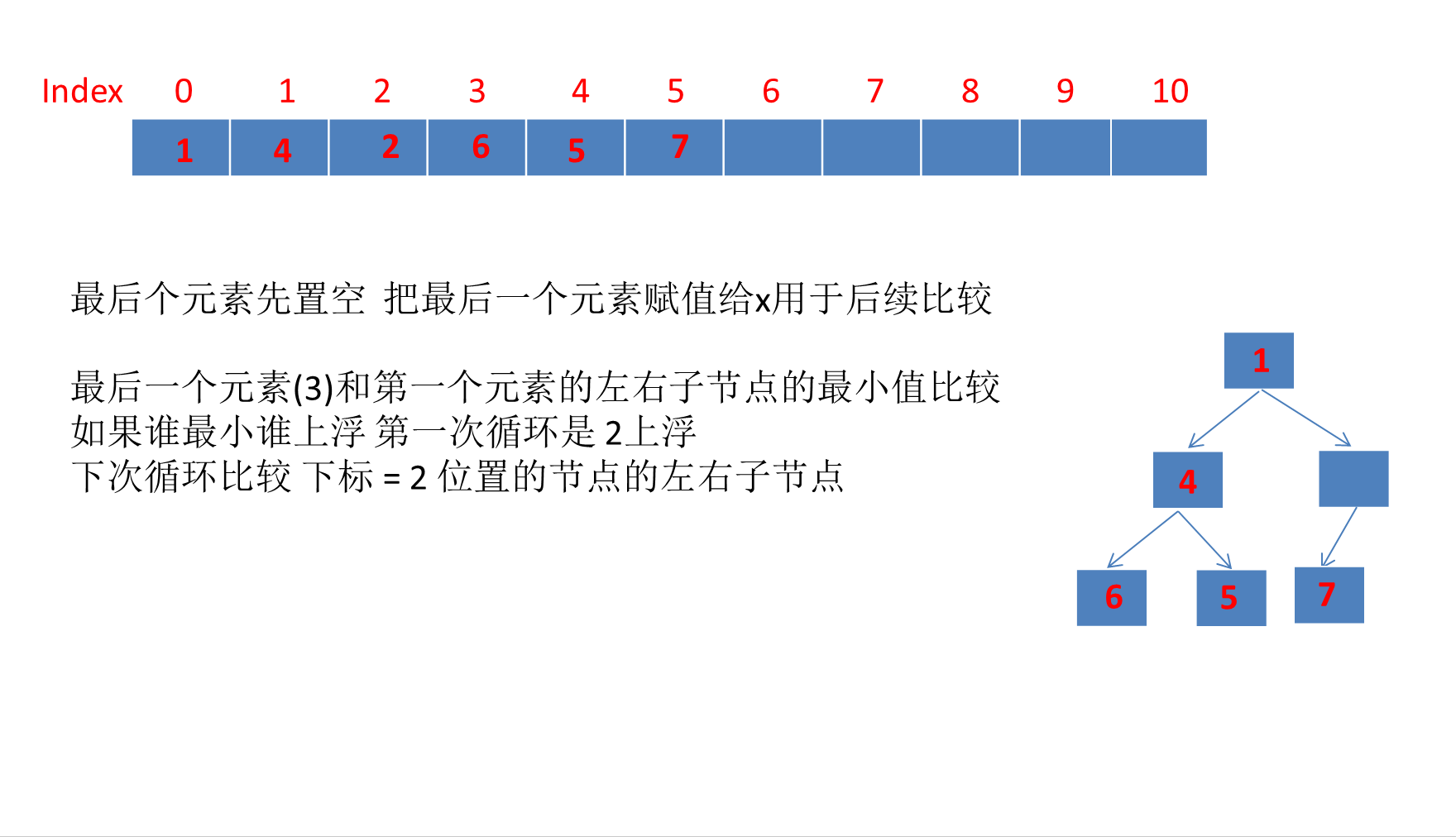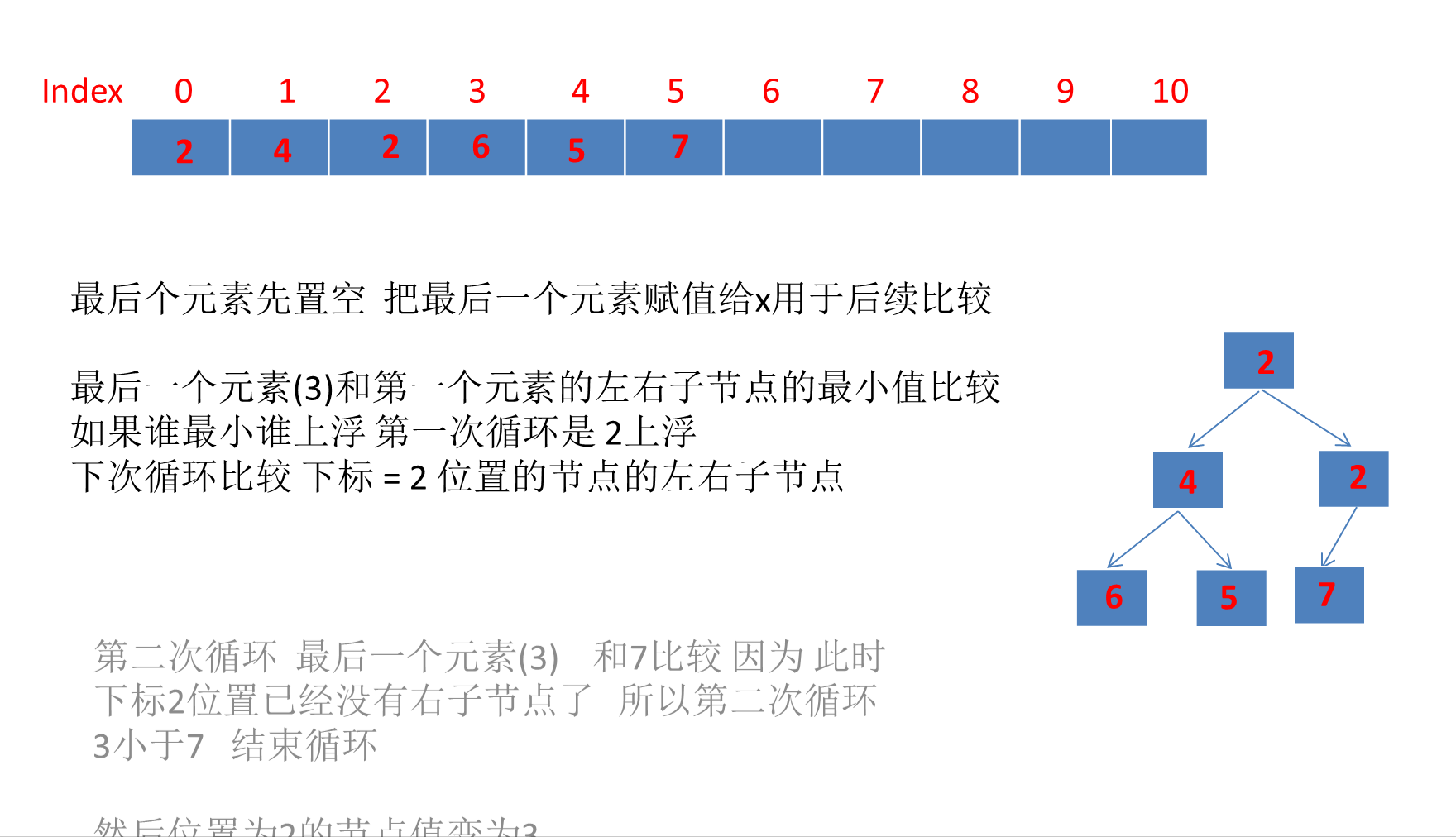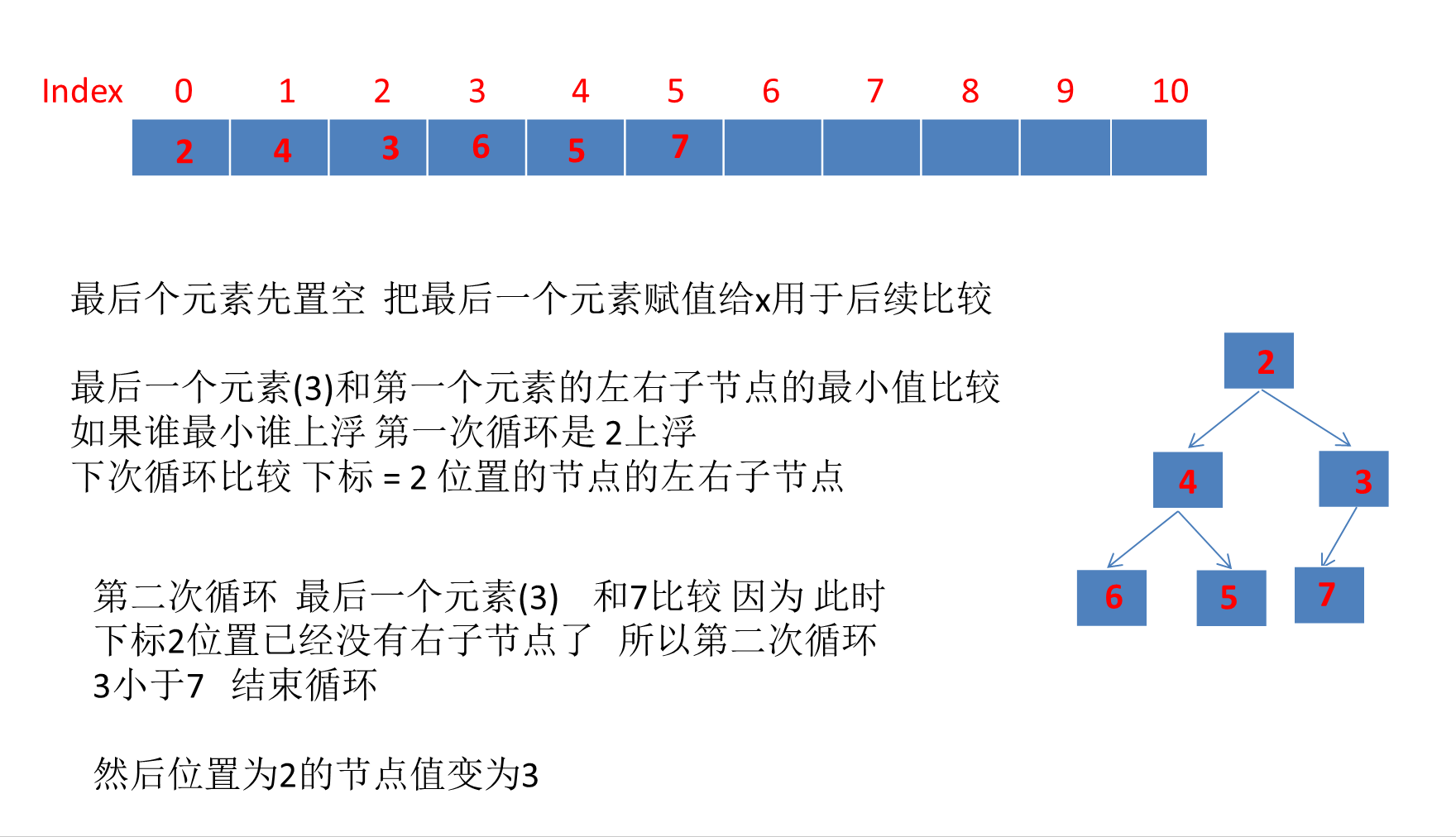
目录 PriorityQueue详解1、PriorityQueue简介2、PriorityQueue继承体系3、PriorityQueue数据结构PriorityQueue类属性注释完全二叉树、大顶堆、小顶堆的概念☆PriorityQueue是如何利用数组存储小顶堆的?☆利用数组存储完全二叉树的好处? 4、PriorityQueu…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...
