DS:二叉树的链式存储及遍历
欢迎来到Harper.Lee的学习世界!
博主主页传送门:Harper.Lee的博客主页
想要一起进步的uu可以来后台找我哦!
一、引入
1.1 二叉树的存储方式
在之前接触到的满二叉树和完全二叉树使用的是数组的存储方式(DS:树与二叉树的相关概念):二叉树因为是顺序结构,比较适合数组形式的存储,但如果不是这两种树形结构,而是其他非完全二叉树,如果用数组实现,那数组的中间部分就可能会存在大量的空间浪费,因此就不适合数组存储,而采用的是链式存储方式。
二叉树使用的是链式结构存储,即使用链表来存储二叉树,就不会有上述的缺陷。链式结构中有左孩子指针和右孩子指针,如果少了左孩子或者右孩子,就让相应的指针置为NULL即可。
虽然链式结构可以表示所有类型的二叉树,但是由于二叉树本身存储数据的价值并不大(链表、顺序表远远优于二叉树),所以实现增删查改是没有太大意义的,学习链式二叉树真正的意义是学会如何去控制、遍历二叉树的结构,为我们后期学习搜索二叉树做好铺垫。而以下的学习中要重点理解二叉树中的递归思想和分治思想!
1.2 二叉树的应用之一——搜索二叉树
二叉树常用的应用方式就是搜索二叉树,搜索二叉树的特点:左子树的所有值比根节点小,右子树的所有值比根节点大,如下图。(左子树<根<右子树)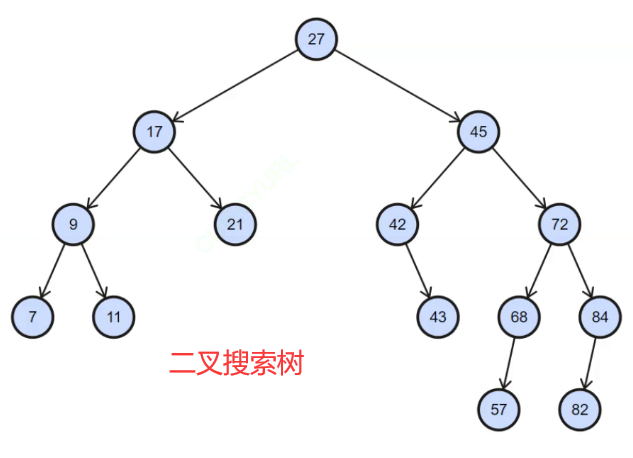
为什么叫二叉搜索树呢?顾名思义,它有数据的搜索功能。例如,查找数据43:43比27大,搜索范围变成右子树,43比45小,搜索范围在左子树,43比42大,搜索范围在右子树,43=43,查找到该数据,且搜索范围逐渐缩小了。
这种查找方式有点类似于二分法,但是二者有很大的不同,搜索二叉树比它效率高好几倍:
| 对比 | 1. 二分法 | 2. 二叉搜索树 |
|---|---|---|
| 数据的存储方式 | 数组存储,增删查改效率低:可能会涉及到数据的挪动等 | 左子树的所有值比根节点小,右子树的所有值比根节点大 可适用于各种类型的数据,但同一棵树中的数据是同一类型 |
| 要求 | 需要排序:排序本身消耗就大 | 不要求排序,兄弟之间无序,父子之间谁大谁当爹或者谁小谁当爹 |
| 二分法在实际中本就不常用 | 二叉搜索树的最大缺陷:不适用于单支的树状结构(如下图) |
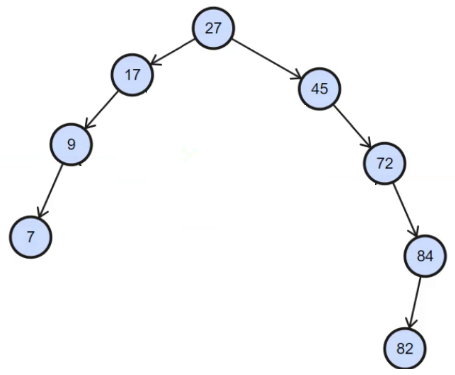
本次搜索二叉树的学习主要有两个目的:1. 最注重的是为后面的学习打基础:对于二叉树的学习,不只是有搜索二叉树,还有AVL树红黑树等二叉平衡搜索树、B数系列多叉平衡搜索树等,他们的基础都在搜索二叉树上。2. 本次学习重点还需要理解二叉树中的递归思想和分治思想。
二、链式二叉树的实现
2.1 相关结构体
typedef int BTDataType;typedef struct BinaryTreeNode
{BTDataType data;//二叉树节点的数据域struct BinaryTreeNode* left;//左孩子struct BinaryTreeNode* right;//右孩子
}BTNode;//重命名为比较简单的名字
2.2 手搓一棵树
在之前学习链表的时候,我们是先插入数据来进行对实现的功能的测试;数组测试我们可以直接给一个数组。同样在这里首先我们需要创建一棵树,才能进行测试,二叉树的增删查改没啥意义,加入二叉搜索树后就有意义了。手搓二叉树只是为了方便测试。
//手搓一棵二叉树
BTNode* CreatBinaryTree()
{//1. 先创建6个节点BTNode* node1 = BuyNode(1);//2. BuyNode节点创建函数的实现BTNode* node2 = BuyNode(2);BTNode* node3 = BuyNode(3);BTNode* node4 = BuyNode(4);BTNode* node5 = BuyNode(5);BTNode* node6 = BuyNode(6);//3. 用left、right连接节点,使其变成自己想要的树的形状node1->left = node2;node1->right = node4;node2->left = node3;node4->left = node5;node4->right = node6;return node1;//直接返回根节点,有了根节点,就有了左膀右臂,直接开火车就可以找到整棵树
}
三、遍历
链式二叉树的增删查改操作没有太大的实际意义,因此我们主要探索的是它的遍历方式。**对于任意一棵树,访问的顺序有三种:前序(前根遍历)、中序(中根遍历)、后序(后根遍历)。 **
3.1 前序遍历(Preorder Traversal )
3.1.1 代码实现
//前序遍历
void PrevOrder(BTNode* root)
{//1. 判空if (root == NULL){printf("N ");//为空的地方打印N,这样更能表示出访问的位置return;}//可以不写else//2. 开始前序遍历//3. 先访问根(打印根节点的数据)printf("%d ", root->data);//4. 再访问左子树leftPrevOrder(root->left);//5. 最后访问右子树PrevOrder(root->right);
}
3.1.2 分析过程
逻辑过程分析(使用代码进行分析):这里其实就是在重复执行一套指令,只不过我为了更加形象地描述它,选择了用代码展开分析讨论。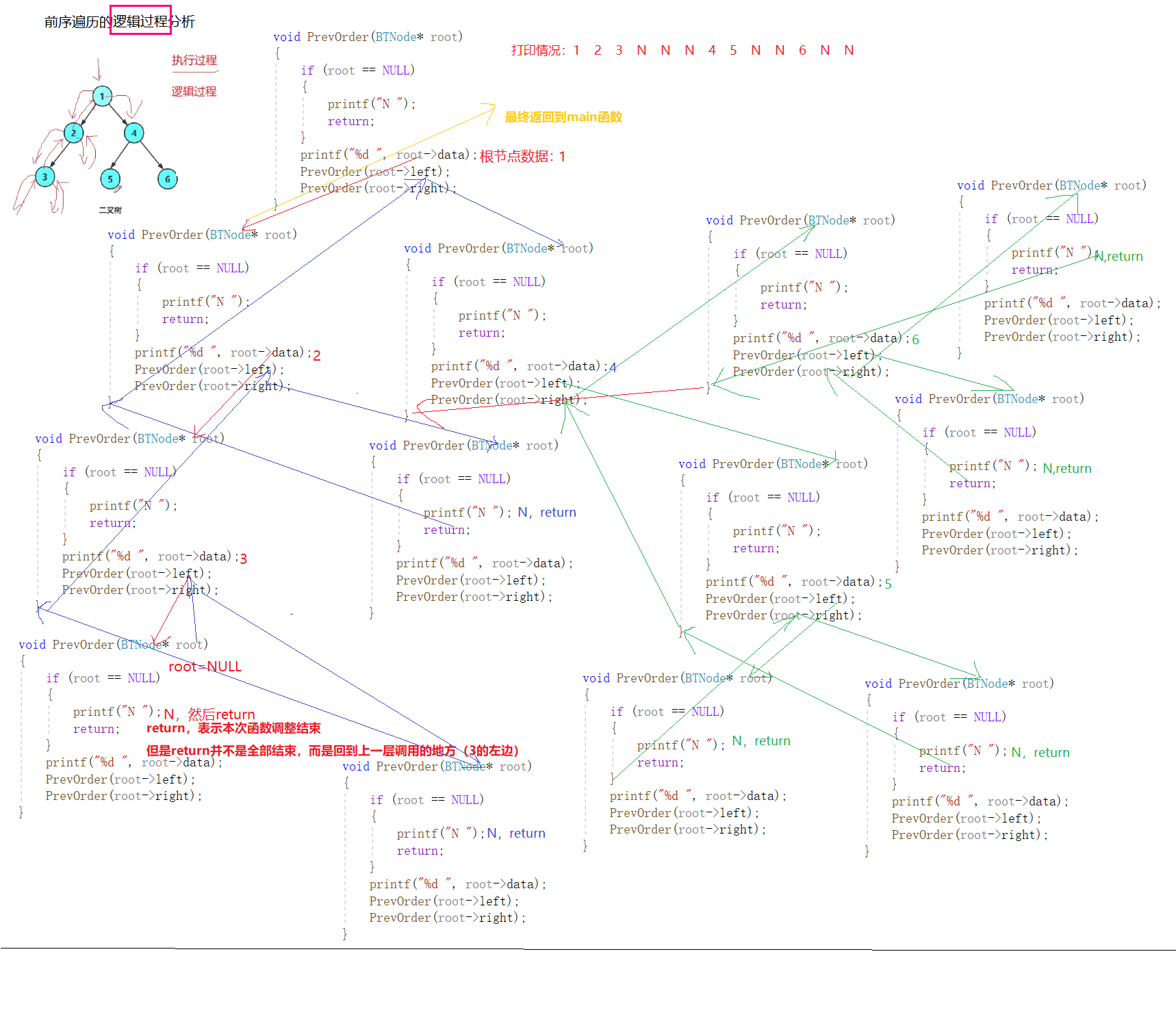
物理过程分析:函数调用是建立栈桢的过程,每个函数调用都是独立的栈桢,调用结束,栈桢销毁。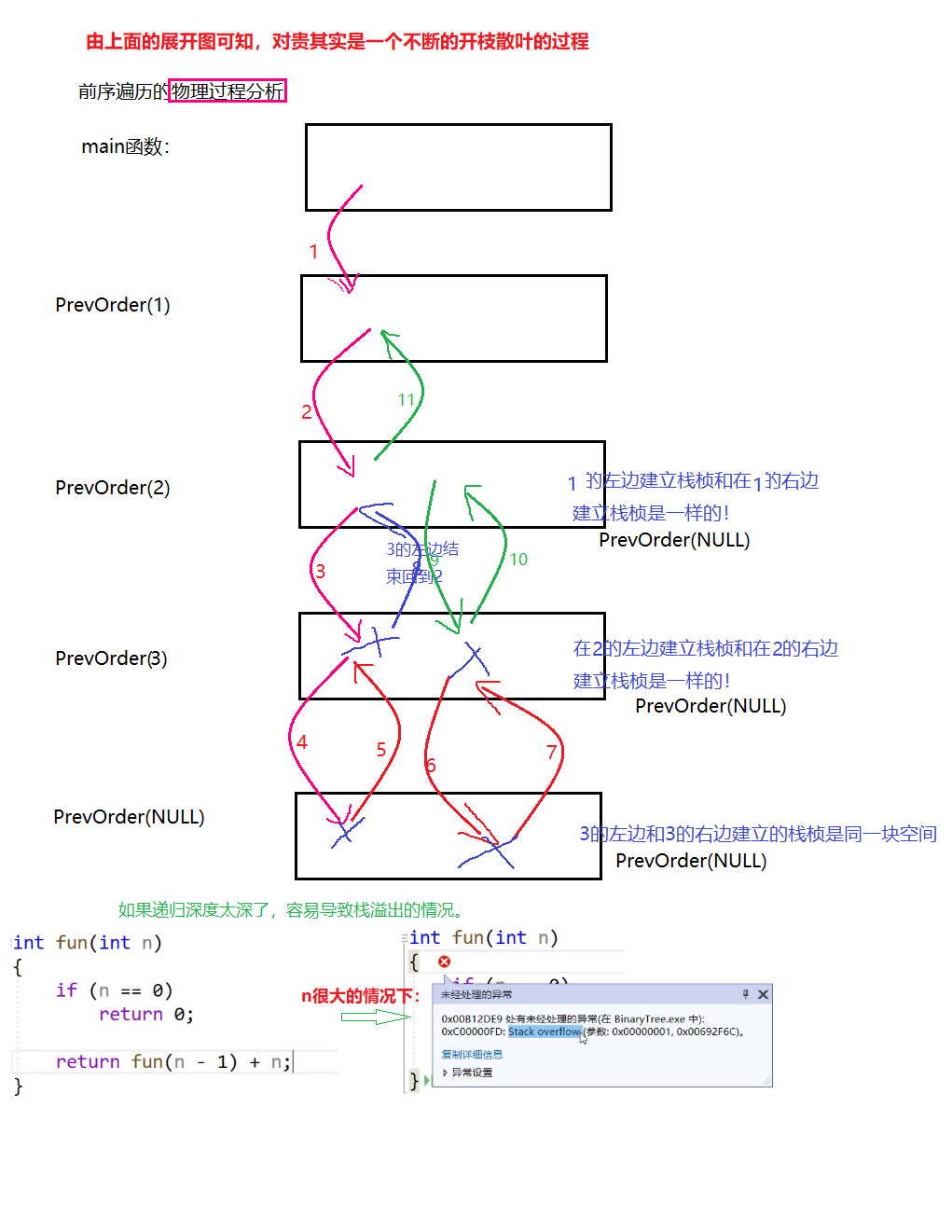
如果递归深度太深了,容易导致栈溢出的情况。 如上图的最后。
根据上述画图中,我们可以知道,PrevOrder函数的递归调用过程中一直在重复使用同一套指令。一套指令重复使用多次,只是每次传入的参数不同,参数不同,执行的逻辑就不同,树状开枝散叶的成都也就不同。此过程中,函数递归的调用并不是死循环的调用,它会遇到NULL,通过return结束该小部分的函数调用,返回上一个调用的函数。
此外,函数递归调用时的参数是存储在栈中的。每个函数调用都是独立的栈桢,栈桢之间相互独立。
3.2 中序遍历(Inorder Traversal)
中序遍历分析的逻辑过程、逻辑过程和前序遍历是一样的分析方法,只需照猫画虎即可。
//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->data);InOrder(root->right);
}
3.3 后序遍历(Postorder Traversal)
后序遍历的物理过程和逻辑过程和前序遍历的分析方式一样。
3.4 层序遍历(BFS)
层序遍历是一种广度优先遍历(BFS),
四、对树的相关计算
4.1 递归的分治思想
 我们一般在没写出代码的时候就很难画出像3.1.2那样的分析图的,因此,在不知道代码如何写的情况下,我们选择递归的分治思想,大概分析出整个过程的思维框架,以便于更好地写出代码。下图是以树的节点个数为例子的一种分析过程:
我们一般在没写出代码的时候就很难画出像3.1.2那样的分析图的,因此,在不知道代码如何写的情况下,我们选择递归的分治思想,大概分析出整个过程的思维框架,以便于更好地写出代码。下图是以树的节点个数为例子的一种分析过程: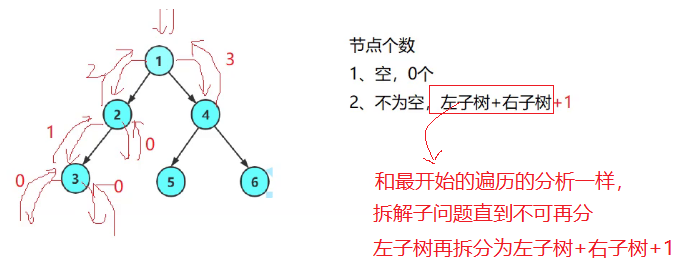
根据上图再逐步接触对应的代码。
//分治思想求树的节点个数
int TreeSize(BTNode* root)
{return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
分治,即分而治之,类似于上下级的管理。例如校长要求学校中统计在校学生人数、在校师生人数等。校长肯定不是自己挨个地去数人数,而是通过各种管理层统计后进行汇总。就像各个班长汇总数据给辅导员,各个辅导员汇总数据给院长,各个院长再汇总数据给校长,校长就得到了最终的数据。
在这个管理层中,级别最低的就是没当班长的学生,他们就是这个管理树中的叶子节点。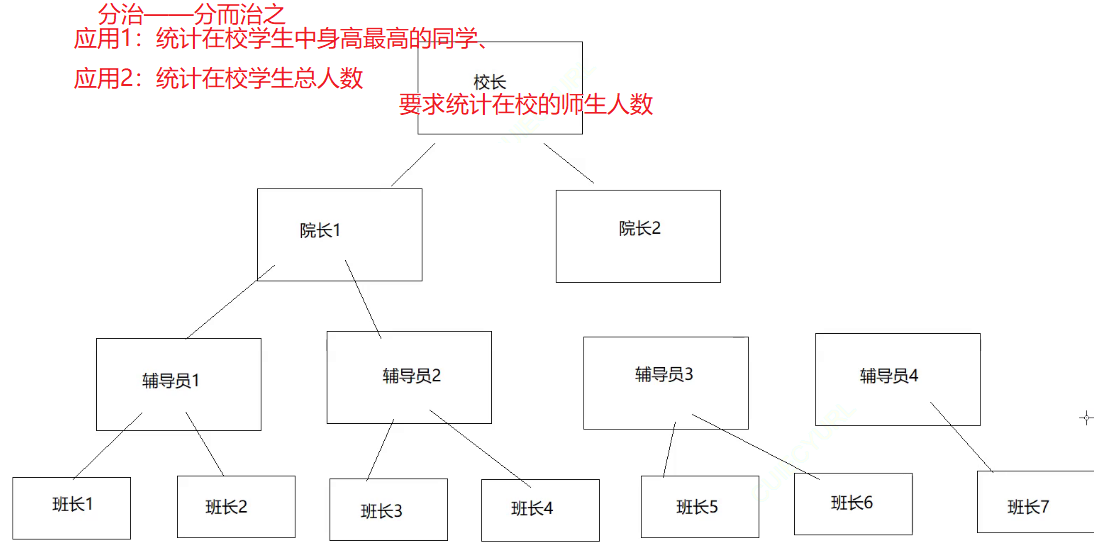
4.2 求树的节点个数
(1)错误代码
//求节点个数的错误代码
int TreeSzie(BTNode* root)
{static int size = 0;//size定义为静态变量:局部静态只会初始化一次,即在第一次的时候才会初始化,其他都是直接积累就用了//如果树为空树if (root == NULL)return 0;else++size;//树不是空树//开始遍历(遍历方式随便一种,这里是前序遍历)TreeSzie(root->left);TreeSzie(root->right);return size;
}
(2)正确代码
a. 定义全局变量
//求节点个数
int size = 0;//定义为全局变量int TreeSzie(BTNode* root)
{//如果树为空树if (root == NULL)return 0;else++size;//树不是空树//开始遍历(遍历方式随便一种,这里是前序遍历)TreeSzie(root->left);TreeSzie(root->right);return size;
}
b. 定义指针
int TreeSize(BTNode* root,int* psize)
{if (root == NULL)return 0;else++(*psize);//遍历树的任一方式:TreeSize(root->left, psize);TreeSize(root->right, psize);return *psize;//可以不用返回值,返回类型为void
}
4.3 二叉树的叶子节点个数
注意不要忽略空树的情况,空树进入函数,->相当于解引用,堆空指针解引用报错!
//求叶子节点的个数
int TreeLeafSize(BTNode* root)
{if (root == NULL)return 0;else if (root->left && root->right)return 1;elsereturn TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
4.4 二叉树的高度
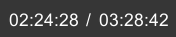
欲扬先抑,要求这个,我就先找下面另外一个,就像校长统计在校师生人数一样,校长直接找各位院长得到数据+1汇总,而院长直接就是各位辅导员数据+1汇总,辅导员数据为班长数据+1(班长自己),层层向下,就像命令在传递一样。班长得到数据后返回辅导员,辅导员得到班长数据后返回院长,院长得到辅导员数据后返回校长,整个过程一来一回,数据就统计出来了。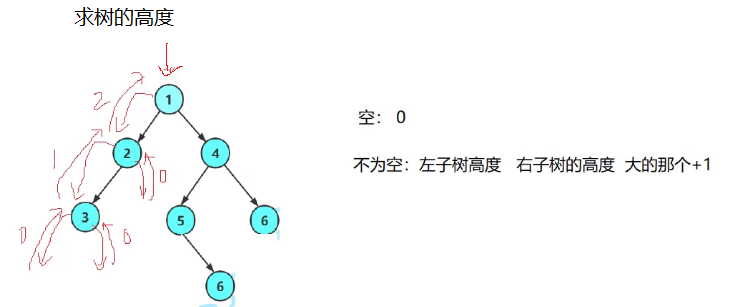
//求树的高度
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;elsereturn TreeHeight(root->left) > TreeHeight(root->right) + 1 ?TreeHeight(root->left) : TreeHeight(root->right) + 1;
}
缺陷:如果该二叉树是一个节点的高度很大的树,那么每个位置会出现重复计算的情况,且重复计算并不一定是两次,可能会重复计算多次。因此我们需要用变量记录每次计算的结果,若还需要该结果,可直接使用该变量。就是在这一点上,我们常常错误的认为重复计算两次即时间消耗为2倍,其实时间消耗远不止2倍。分析过程如下图。
//求树的高度
//时间复杂度:O(N)
int TreeHeight(BTNode* root)
{if (root == NULL)return 0;//保存记录数据int leftHeight = TreeHeight(root->left);int rightHeight = TreeHeight(root->right);//可以使用fmax函数return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

这就相当于不记事的某一层领导因为忘记数据,又再安排下层领导一次,该领导这条路就又重复一次。
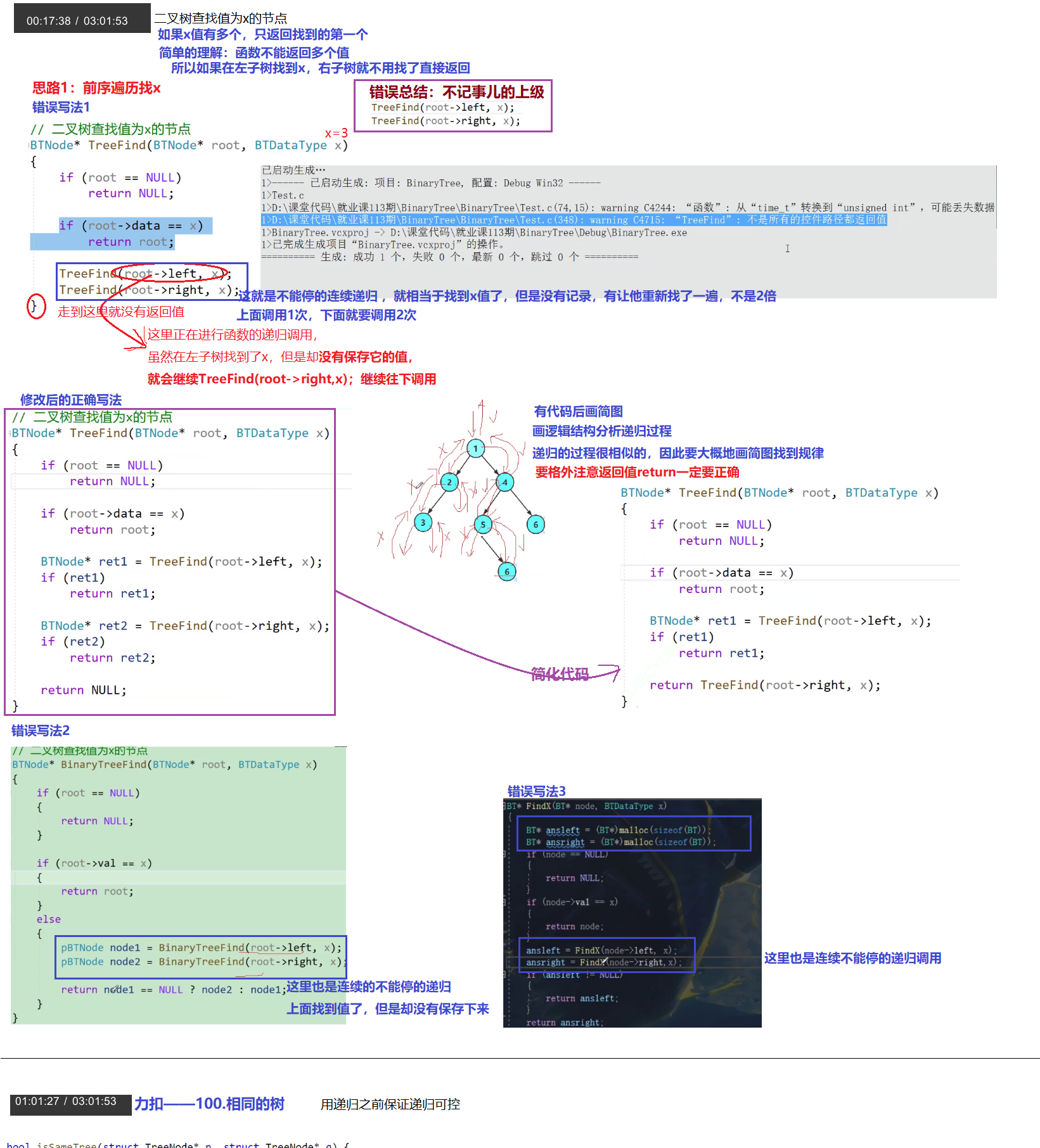
4.5 二叉树查找值为x的节点
(1)分析过程如下:
(2)代码实现
//二叉树中查找值为x的节点
BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)retur NULL;if (root->data == x)return root;BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}
改进版本:
//改进版本:
BTNode* _BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL)retur NULL;if (root->data == x)return root;BTNode* ret1 = _BinaryTreeFind(root->left, x);if (ret1)return ret1;return _BinaryTreeFind(root->right, x);
}
喜欢的朋友记得三连支持哦!

相关文章:

DS:二叉树的链式存储及遍历
欢迎来到Harper.Lee的学习世界! 博主主页传送门:Harper.Lee的博客主页 想要一起进步的uu可以来后台找我哦! 一、引入 1.1 二叉树的存储方式 在之前接触到的满二叉树和完全二叉树使用的是数组的存储方式(DS:树与…...

C#中File类常见用法总结
前言 我们在开发C#软件的过程中,经常需要和文件打交道,那么File类在C#中是我们使用非常频繁的一个类,本文就是详细介绍File类在C#中的常见用法。 1、判断文件是否存在 string fileName "1.txt";bool isExist File.Exists(fileN…...

CesiumJS【Basic】- #007 绘制直线段以避免地球曲率的影响
文章目录 绘制直线段以避免地球曲率的影响1 目标2 实现绘制直线段以避免地球曲率的影响 1 目标 绘制直线段以避免地球曲率的影响 2 实现 在CesiumJS中,直线的弯曲是由地球曲率引起的,因为地球是一个球体而不是一个平面。因此,如果您要在地球上绘制两点之间的直线,它将会…...

解决文件或文件夹无法删除问题
最近呢,发现很多小伙伴都会遇到一个问题,就是当我要删掉一个文件或者软件的时候,就会弹出[操作无法完成,因为其中的文件夹或文件已在另一个程序中打开] 然后我就翻看网站,很多都是什么去**[任务管理器]修改[资源管理器…...
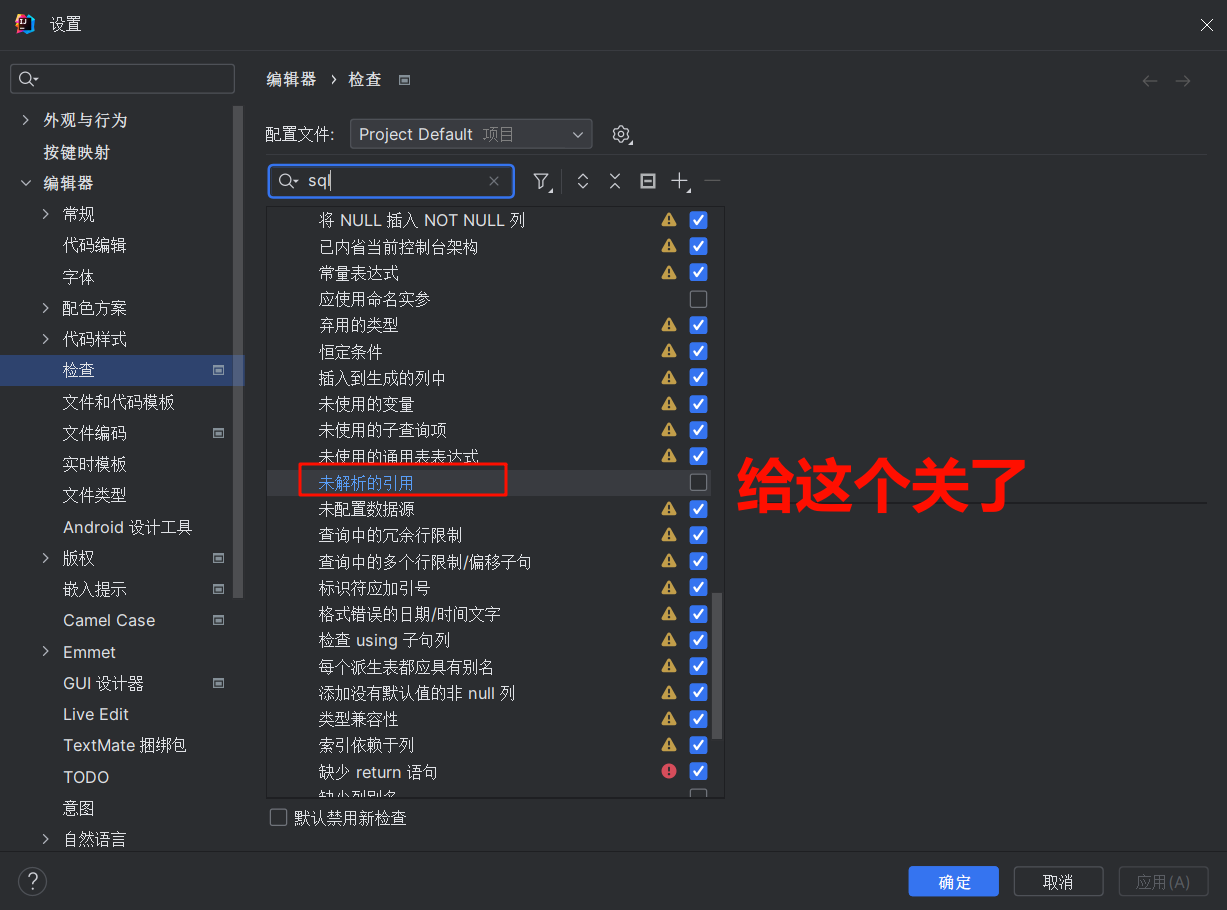
【报错】JDBC SQL语句表名报错 解决办法
解决办法 修改检测等级 不是检测有问题吗,那就将idea的检测问题取消掉或者修改检测问题等级,根本问题上我们写的sql语句是一个字符串传过去,只要在mysql查询语句能够正确执行,不要这种检测也罢。...

【Nvidia+AI摄像头】面向机器人双目视觉相机
随着人工智能和机器人技术的不断发展,双目深度相机作为一种重要的传感器,正在被广泛应用于各种机器人系统中。双目深度相机作为机器人不可或缺的感知器件,其高精度深度信息为机器人提供环境感知、立体视觉、姿态识别等功能,让机器…...

Hive数据锁问题处理
在测试环境有定时任务会定期将flume采集的数据load到hive表中,在查看yarn application过程中发现load操作没有执行,且后续的任务在上一个任务执行结束后很久才开始。感觉像是阻塞一样,于是手动执行相关脚本,发现也是会卡住&#x…...

使用VisualBox+Vagrant搭建Centos虚拟机环境
1.下载并安装VisualBox; 2.下载并安装Vagrant; 3.打开cmd窗口,执行命令vagrant init centos/7,初始化centos环境,该步骤受网络带宽影响,可能挂级30分钟到1个小时; 4.启动虚拟机:vagrant up&…...

PHP框架之Yii框架
Yii框架详细说明 Yii框架是一个基于组件的高性能PHP框架,用于开发大型Web应用。Yii框架由薛强创立,自2008年1月1日开始开发,至今已成为PHP开发领域的佼佼者之一。Yii框架以其高效、安全、灵活和可扩展的特性,赢得了众多开发者的青…...

数组元素去重
1 .旧数组不重复的元素放到新数组 2 .遍历旧数组,拿旧数组查新数组,如果元素在新数组内没有出现过就添加 3 .利用 新数组.indexOf(数组元素) 如果返回-1就说明新数组里没有该元素 //封装一个 去重的函数 function unique(arr) {var newArr[];for(var …...

Redis 的安装与部署
本文为Redis的Linux版单机部署。 上传 redis-3.2.8 源码到 /opt/software/ 解压到 /opt/module/ [huweihadoop101 software]$ tar -zxvf redis-3.2.8.tar.gz -C /opt/module/安装依赖 [huweihadoop101 software]$ sudo yum -y install gcc-c tclRedis是C语言编写的 编译安装…...
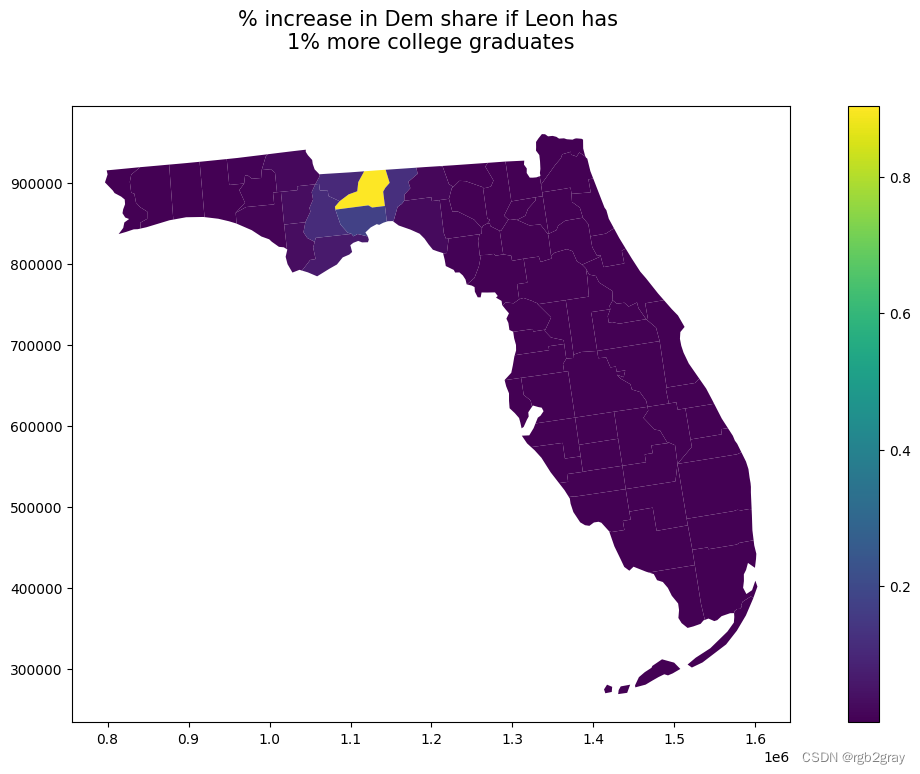
Applied Spatial Statistics(七):Python 中的空间回归
Applied Spatial Statistics(七):Python 中的空间回归 本笔记本演示了如何使用 pysal 的 spreg 库拟合空间滞后模型和空间误差模型。 OLS空间误差模型空间滞后模型三种模型的比较探索滞后模型中的直接和间接影响 import numpy as np impor…...
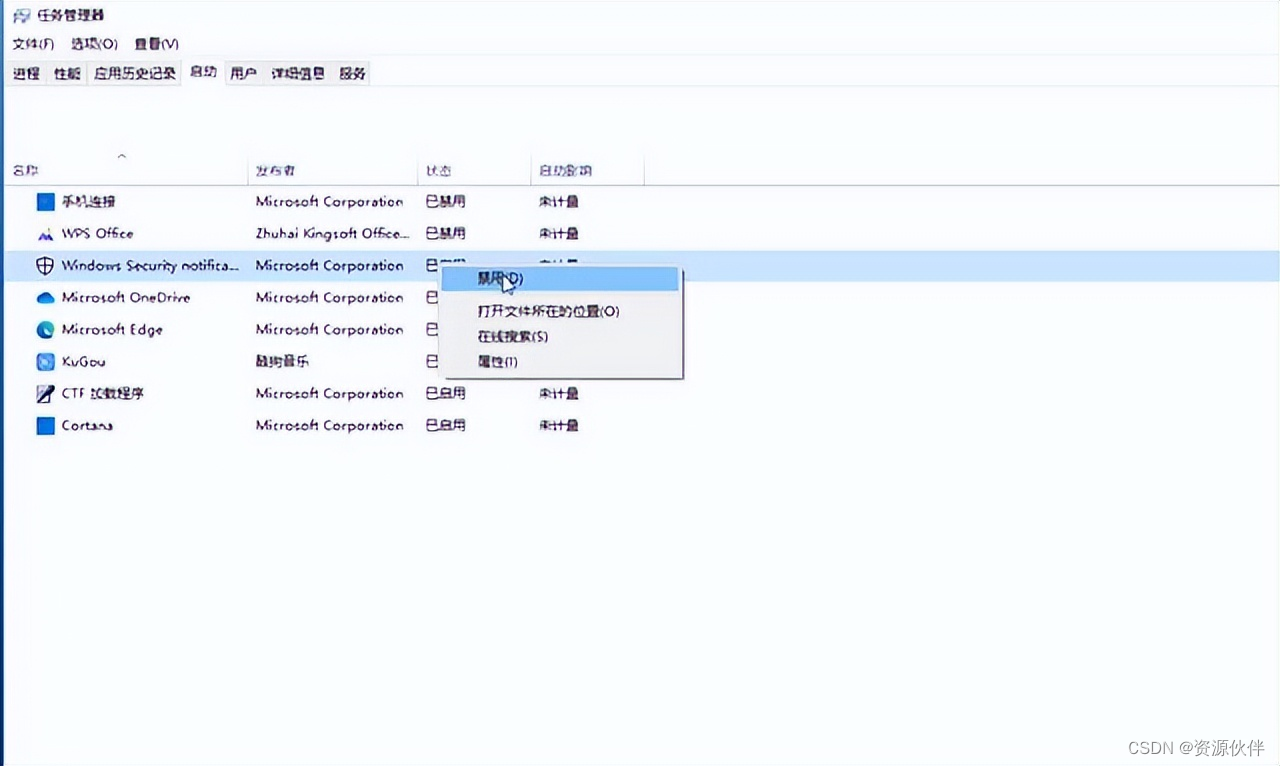
如何关闭软件开机自启,提升电脑开机速度?
如何关闭软件开机自启,提升电脑开机速度?大家知道,很多软件在安装时默认都会设置为开机自动启动。但是,有很多软件在我们开机之后并不是马上需要用到的,开机启动的软件过多会导致电脑开机变慢。那么,如何关…...

如何培养员工的竞争意识
一、背景 在当今快速变化的商业环境中,培养员工的竞争意识对于企业的长期成功至关重要。通过激发员工的竞争精神,企业能够提升整体绩效,增强创新能力,并在市场竞争中保持领先地位。本文将从多个方面探讨如何培养员工的竞争意识。 二、明确目标设定 设定清晰具体的目标:明…...

2025秋招NLP算法面试真题(二)-史上最全Transformer面试题:灵魂20问帮你彻底搞定Transformer
简单介绍 之前的20个问题的文章在这里: https://zhuanlan.zhihu.com/p/148656446 其实这20个问题不是让大家背答案,而是为了帮助大家梳理 transformer的相关知识点,所以你注意看会发现我的问题也是有某种顺序的。 本文涉及到的代码可以在…...
)
redis初步认识(一)
文章目录 概述安装编译 string数据结构基础命令应用对象存储累加器 list结构基础命令应用栈(先进后出FILO)队列 HASH基础命令存储结构应用存储对象 小结 概述 redis 是一个远程字典服务;当然,redis是内存数据库,kv数据库,最基础的…...
Android 开发必备知识点及面试题汇总(Android+Java+算法+性能优化+四大组件……
**虚引用:**顾名思义,就是形同虚设,如果一个对象仅持有虚引用,那么它相当于没有引用,在任何时候都可能被垃圾回收器回收。 7.介绍垃圾回收机制 **标记回收法:**遍历对象图并且记录可到达的对象,…...

安装Cmakeffmpeglibssh
首先安装cmake: sudo apt install cmake cmake --version然后这个输出正常就装好了 然后安装ffmpeg: tar xvzf n4.4.tar.gz cd FFmpeg-n4.4 chmod x configure ./configure --enable-gpl --enable-nonfree --enable-libx264 --enable-debug --disable-opti…...
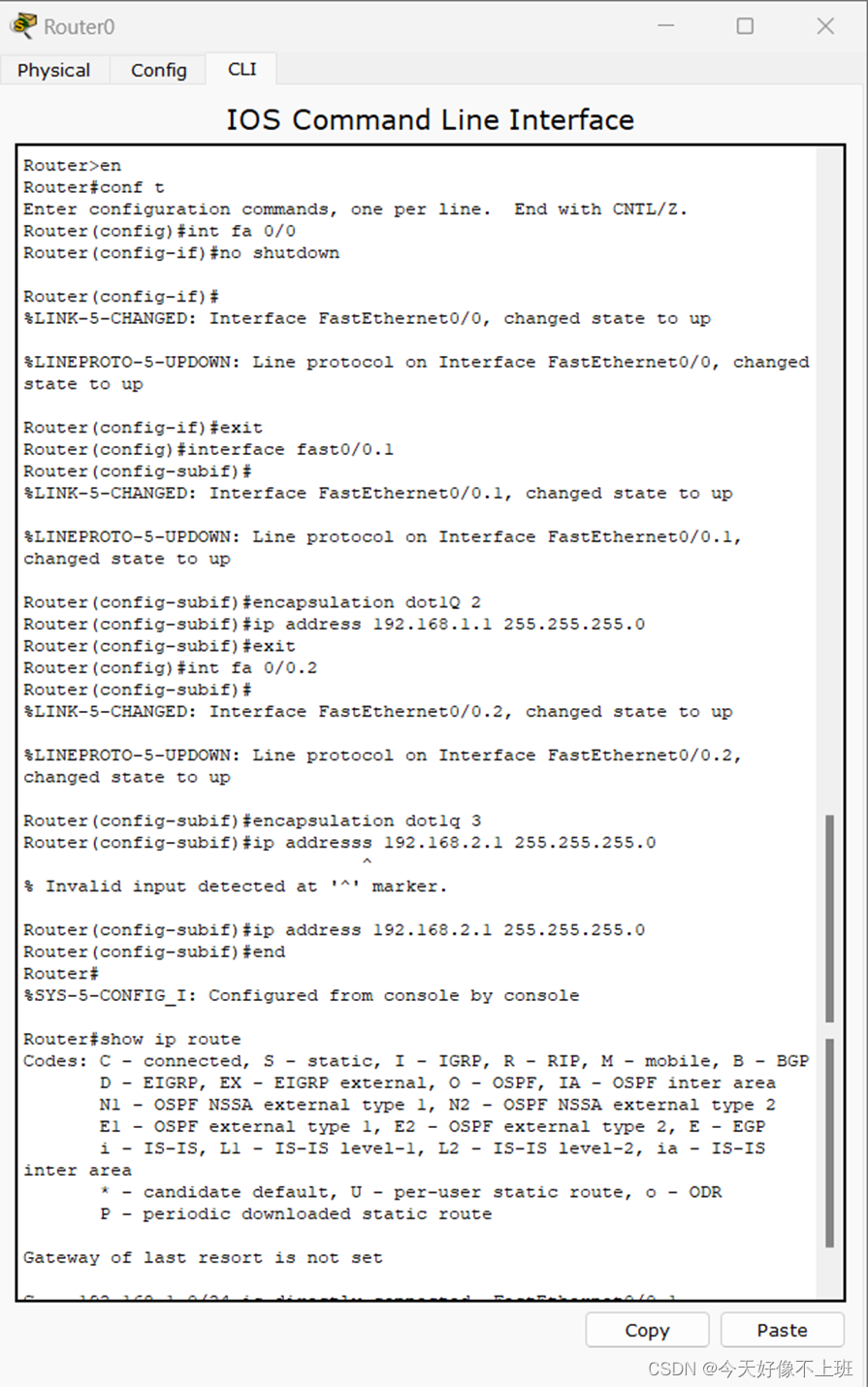
计算机网络实验(9):路由器的基本配置和单臂路由配置
一、 实验名称 路由器的基本配置和单臂路由配置 二、实验目的: (1)路由器的基本配置: 掌握路由器几种常用配置方法; 掌握采用Console线缆配置路由器的方法; 掌握采用Telnet方式配置路由器的方法&#…...
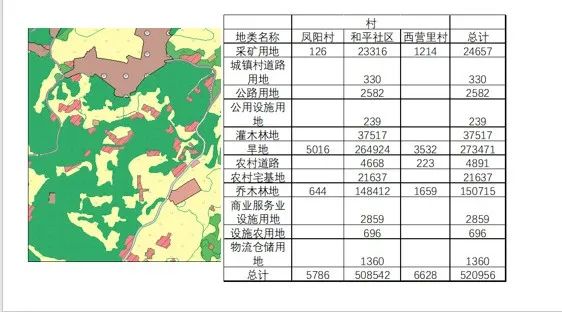
ArcGIS与Excel分区汇总统计三调各地类面积!数据透视表与汇总统计!
点击下方全系列课程学习 点击学习—>ArcGIS全系列实战视频教程——9个单一课程组合系列直播回放 点击学习——>遥感影像综合处理4大遥感软件ArcGISENVIErdaseCognition 01 需求说明 介绍一下ArcGIS与Excel统计分区各地类的三调地类面积。 ArcGIS统计分析不会&#x…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

CMake 从 GitHub 下载第三方库并使用
有时我们希望直接使用 GitHub 上的开源库,而不想手动下载、编译和安装。 可以利用 CMake 提供的 FetchContent 模块来实现自动下载、构建和链接第三方库。 FetchContent 命令官方文档✅ 示例代码 我们将以 fmt 这个流行的格式化库为例,演示如何: 使用 FetchContent 从 GitH…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

【网络安全】开源系统getshell漏洞挖掘
审计过程: 在入口文件admin/index.php中: 用户可以通过m,c,a等参数控制加载的文件和方法,在app/system/entrance.php中存在重点代码: 当M_TYPE system并且M_MODULE include时,会设置常量PATH_OWN_FILE为PATH_APP.M_T…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

【SpringBoot自动化部署】
SpringBoot自动化部署方法 使用Jenkins进行持续集成与部署 Jenkins是最常用的自动化部署工具之一,能够实现代码拉取、构建、测试和部署的全流程自动化。 配置Jenkins任务时,需要添加Git仓库地址和凭证,设置构建触发器(如GitHub…...
