【论文精读】分类扩散模型:重振密度比估计(Revitalizing Density Ratio Estimation)
文章目录
- 一、文章概览
- (一)问题的提出
- (二)文章工作
- 二、理论背景
- (一)密度比估计DRE
- (二)去噪扩散模型
- 三、方法
- (一)推导分类和去噪之间的关系
- (二)组合训练方法
- (三)一步精确的似然计算
- 四、实验
- (一)使用两种损失对于实现最佳分类器的重要性
- (二)去噪结果、图像质量和负对数似然
论文:Classification Diffusion Models: Revitalizing Density Ratio Estimation
一、文章概览
(一)问题的提出
学习数据分布的重要方法:密度比估计(DRE)
- 密度比估计训练模型以在数据样本和来自某个参考分布的样本之间进行分类。
- 优势:基于 DRE 的模型可以直接输出任何给定输入的可能性,这是大多数生成技术所缺乏的非常理想的属性
- 劣势:DRE 方法一直难以准确捕获图像等复杂高维数据的分布
复杂高维数据的生成建模:去噪扩散模型(DDM)
- 优势:可以处理复杂高维数据的生成建模问题,应用于解决逆问题、图像编辑和医学数据增强
- 劣势:评估数据样本的可能性是一项具有挑战性的任务,需要许多神经函数评估(NFE)来计算可能性 - ELBO,或使用 ODE 求解器来近似精确的可能性。
(二)文章工作
提出分类扩散模型(CDM):基于DRE的生成方法
- 采用去噪扩散模型(DDM)的形式
- 利用分类器来预测添加到干净信号中的噪声水平
- 将预测添加到数据样本中的高斯白噪声水平的最佳分类器与清除这种噪声的 MMSE 降噪器之间建立了连接
- DDMs依赖于最小均方误差(MMSE)去噪
- DRE方法则依赖于最优分类
二、理论背景
(一)密度比估计DRE
噪声对比估计(NCE)方法:
-
从最优二元分类器中提取未知分布 p d ( x ) p_d(x) pd(x) 和已知参考分布 p n ( x ) p_n(x) pn(x) 之间的比率,以区分 p d ( x ) p_d(x) pd(x) 和 p n ( x ) p_n( x) pn(x)。一旦从分类器中提取出该比率,就可以将其乘以已知的 p n ( x ) p_n(x) pn(x) 以获得 p d ( x ) p_d(x) pd(x)。
-
具体来说,令 C C C表示样本 x x x的类别,其中 C C C = 1、0分别对应于 x x x 是来自 p d ( x ) p_d(x) pd(x)、 p n ( x ) p_n(x) pn(x)的样本的事件。从 x x x 预测 C C C 的最佳分类器输出 P ( C = 1 ∣ x ) P(C = 1|x) P(C=1∣x) 和 P ( C = 0 ∣ x ) P(C = 0|x) P(C=0∣x)。使用贝叶斯规则可以计算密度比
p d ( x ) p n ( x ) = P ( C = 1 ∣ x ) P ( C = 0 ∣ x ) \frac{p_d(x)}{p_n(x)}=\frac{P(C=1|x)}{P(C=0|x)} pn(x)pd(x)=P(C=0∣x)P(C=1∣x)
DRE的密度断层问题:
当目标分布 p d ( x ) p_d(x) pd(x) 和已知参考分布 p n ( x ) p_n(x) pn(x)差异显著时,传统的密度比估计(DRE)方法可能会失败。因为当训练一个分类器来区分图像和噪声时,分类器可以在不学习有关图像的有意义信息的情况下达到高精度。一旦分类器达到这一点,其权重实际上会停止更新。
TRE方法:
使用一系列列逐渐接近的分布 p x 0 ( x ) , p x 1 ( x ) , . . . , p x m ( x ) p_{x0}(x),p_{x1}(x),...,p_{xm}(x) px0(x),px1(x),...,pxm(x),其中 p x m ( x ) p_{xm}(x) pxm(x)是参考分布,而 p x 0 ( x ) p_{x0}(x) px0(x)是目标分布。中间的分布 { p x i ( x ) } i = 1 m − 1 \{p_{xi}(x)\}_{i=1}^{m-1} {pxi(x)}i=1m−1不需要事先知道具体形式,只要能够从中采样即可。
- 定义 p x i ( x ) p_{xi}(x) pxi(x)为 x i = α ˉ i x 0 + 1 − α ˉ i x m x_i=\sqrt{\bar{\alpha}_i}x_0+\sqrt{1-\bar{\alpha}_i}x_m xi=αˉix0+1−αˉixm,其中 x 0 ∼ p x 0 , x m ∼ p x m x_0\sim p_{x0},x_m\sim p_{xm} x0∼px0,xm∼pxm, α ˉ i \bar{\alpha}_i αˉi是一个从1逐渐减少到0的序列;
- 利用密度比估计的原理,可以通过训练二元分类器来区分来自 p x i ( x ) p_{xi}(x) pxi(x)和 p x i + 1 ( x ) p_{xi+1}(x) pxi+1(x)的样本,提取每对相邻分布 p x i ( x ) / p x i + 1 ( x ) p_{xi}(x)/p_{xi+1}(x) pxi(x)/pxi+1(x)的比值;
- 计算出目标分布和参考分布之间的比值:
p x 0 ( x ) p x m ( x ) = p x 0 ( x ) p x 1 ( x ) ⋅ p x 1 ( x ) p x 2 ( x ) ⋅ . . . ⋅ p x m − 2 ( x ) p x m − 1 ( x ) ⋅ p x m − 1 ( x ) p x m ( x ) \frac{p_{x0}(x)}{p_{xm}(x)}=\frac{p_{x0}(x)}{p_{x1}(x)}\cdot \frac{p_{x1}(x)}{p_{x2}(x)}\cdot ... \cdot \frac{p_{xm-2}(x)}{p_{xm-1}(x)}\cdot \frac{p_{xm-1}(x)}{p_{xm}(x)} pxm(x)px0(x)=px1(x)px0(x)⋅px2(x)px1(x)⋅...⋅pxm−1(x)pxm−2(x)⋅pxm(x)pxm−1(x)
优点:通过这种方法,TRE方法通过增加分类任务的复杂度,使得DRE方法能够有效地估计复杂的目标分布 ,而不会受到传统方法中密度断层问题的限制。
缺点:TRE方法中的每个比值 p x i ( x ) p x i + 1 ( x ) \frac{p_{xi}(x)}{p_{xi+1}(x)} pxi+1(x)pxi(x)都是从仅在分布 p x i p_{xi} pxi和 p x i + 1 p_{xi+1} pxi+1上训练的二元分类器中提取出来的,也就是说不同比值是从不同分布上得到的,这可能导致训练和推断时出现不匹配,因为在推断时,所有的比值都是在相同的输入x上评估的。

(二)去噪扩散模型
【论文精读】DDPM:Denoising Diffusion Probabilistic Models 去噪扩散概率模型
DDM作为一个最小均方误差(MMSE)去噪器,其行为受噪声水平条件影响;而CDM则作为一个分类器。对于给定的噪声图像,CDM输出一个概率向量,预测噪声水平。这个概率向量中的第 t t t 个元素表示输入图像的噪声水平对应于扩散过程中的第 t t t 个时间步的概率。CDM可以用来输出MMSE去噪后的图像,方法是根据我们在定理3.1中展示的内容,计算其输出概率向量关于输入图像的梯度。
换句话说,CDM通过输出的概率向量,可以反向推导出输入图像在不同噪声水平下的最小均方误差去噪结果。

三、方法
(一)推导分类和去噪之间的关系
我们首先推导出分类和去噪之间的关系,然后将其用作我们的 CDM 方法的基础。
随机向量 x t x_t xt包含了时间步 t ∈ { 1 , . . . , T } t\in \{1,...,T\} t∈{1,...,T},并设置0和 T + 1 T+1 T+1两个额外的时间步,分别对应干净图像和纯高斯噪声。具体地,定义 α ˉ 0 = 1 \bar{\alpha}_0=1 αˉ0=1 和 α ˉ T + 1 = 0 \bar{\alpha}_{T+1}=0 αˉT+1=0 。每个时刻 t t t随机向量 x t x_t xt的密度为 p x t ( x ) p_{x_t}(x) pxt(x)。
分类器的输出:
文章方法的核心是训练一个分类器,接受一个噪声样本 x t x_t xt,并预测其所在的时刻 t t t。形式上,假设 t t t是一个取值在 { 0 , , 1 , . . . , T , T + 1 } \{0,,1,...,T,T+1\} {0,,1,...,T,T+1}的离散随机变量,概率质量函数为 p t ( t ) = P ( t = t ) p_t(t)=P(t=t) pt(t)=P(t=t),并且随机向量 x ~ \tilde{x} x~是在随机时刻 t t t的扩散信号,即 x ~ = x t \tilde{x}=x_t x~=xt。注意到每个 x t x_t xt的密度可以写成 p x t ( x ) = p x ~ ∣ t ( x ∣ t ) p_{x_t}(x)=p_{\tilde{x}|t}(x|t) pxt(x)=px~∣t(x∣t),根据全概率公式, x ~ \tilde{x} x~的密度为:
p x ~ ( x ) = ∑ t = 1 T + 1 p x t ( x ) p t ( t ) p_{\tilde{x}}(x)=\sum_{t=1}^{T+1}p_{x_t}(x)p_t(t) px~(x)=t=1∑T+1pxt(x)pt(t)
给定从 p x ~ ( x ) p_{\tilde{x}}(x) px~(x)抽样的样本 x x x,我们感兴趣的是一个分类器,输出概率向量 ( p t ∣ x ~ ( 0 ∣ x ) , p t ∣ x ~ ( 1 ∣ x ) . . . , p t ∣ x ~ ( T + 1 ∣ x ) ) (p_{t|\tilde{x}}(0|x),p_{t|\tilde{x}}(1|x)...,p_{t|\tilde{x}}(T+1|x)) (pt∣x~(0∣x),pt∣x~(1∣x)...,pt∣x~(T+1∣x)),其中 p t ∣ x ~ ( t ∣ x ) = P ( t = t ∣ x ~ = x ) p_{t|\tilde{x}}(t|x)=P(t=t|\tilde{x}=x) pt∣x~(t∣x)=P(t=t∣x~=x)。
分类器的梯度就是DDM中的去噪器:
假设我们有一个去噪器,其作用是去除样本中的噪声,这个去噪器可以看作是对分类器输出的概率向量的梯度操作。通过这个梯度操作,我们可以得到每个时间步对应的去噪后的结果。公式表达为:
令 F ( x , t ) = log ( p t ∣ x ~ ( T + 1 ∣ x ) ) − log ( p t ∣ x ~ ( t ∣ x ) ) F(x,t)=\log(p_{t|\tilde{x}}(T+1|x))-\log(p_{t|\tilde{x}}(t|x)) F(x,t)=log(pt∣x~(T+1∣x))−log(pt∣x~(t∣x)),则有:
E ( ϵ t ∣ x t = x t ) = 1 − α ˉ t ( ∇ x t F ( x t , t ) + x t ) E(\epsilon_t|x_t=x_t)=\sqrt{1-\bar{\alpha}_t}(\nabla_{x_t}F(x_t,t)+x_t) E(ϵt∣xt=xt)=1−αˉt(∇xtF(xt,t)+xt)
使用标准交叉熵(CE)损失简单地训练这样的分类器会导致糟糕的结果:
因此,我们可以训练一个分类器,并根据上述公式使用其梯度作为降噪器,然后应用任何所需的采样方法(例如DDPM、DDIM等)。然而,使用标准交叉熵(CE)损失简单地训练这样的分类器会导致糟糕的结果。这是因为即使没有学习到任何时间步 t t t下正确的概率 p t ∣ x ~ ( t ∣ x ) p_{t|\tilde{x}}(t|x) pt∣x~(t∣x),分类器也可能达到较低的 CE 损失。 这种现象可以在下图中观察到,它说明了迄今为止 DRE 方法未能捕获图像等高维复杂数据的分布的原因。

(二)组合训练方法
为了获得任何时间步 t t t下正确的概率 p t ∣ x ~ ( t ∣ x ) p_{t|\tilde{x}}(t|x) pt∣x~(t∣x),我们建议使用一种结合了分类器输出的交叉熵损失和其梯度的均方误差的训练方法。完整训练算法如算法1所示:

算法 2 展示了如何使用 DDPM 采样器通过 CDM 生成样本,而类似的方法也可用于其他采样器。使用 CDM 的 DDPM 采样中的每个步骤 t 由下式给出:
x t − 1 = α t x t − 1 − α t α t ∇ x t F θ ( x t , t ) + σ t z x_{t-1}=\sqrt{\alpha_t}x_t-\frac{1-\alpha_t}{\sqrt{\alpha_t}}\nabla_{x_t}F_\theta(x_t,t)+\sigma_tz xt−1=αtxt−αt1−αt∇xtFθ(xt,t)+σtz
(三)一步精确的似然计算
为了计算给定样本的似然,DDM 需要多次评估神经网络来使用诸如证据下界(ELBO)或者基于ODE求解器来近似对数似然的方法,作为基于DRE的方法,Classifier-Defined Models(CDMs)具有显著优势。CDMs可以在单次神经网络评估(NFE)中计算精确的似然性。具体地,对于任意所需的时间步长t,CDMs可以计算与噪声图像分布 p x t p_{xt} pxt相关的精确似然性。
对于任意 t ∈ { 0 , 1 , . . , T + 1 } t\in \{0,1,..,T+1\} t∈{0,1,..,T+1},有:
p x t ( x ) = p t ( T + 1 ) p t ( t ) p t ∣ x ~ ( t ∣ x ) p t ∣ x ~ ( T + 1 ∣ x ) N ( x ; 0 , I ) p_{x_t}(x)=\frac{p_t(T+1)}{p_t(t)}\frac{p_{t|\tilde{x}}(t|x)}{p_{t|\tilde{x}}(T+1|x)}\mathcal{N}(x;0,\mathcal{I}) pxt(x)=pt(t)pt(T+1)pt∣x~(T+1∣x)pt∣x~(t∣x)N(x;0,I)
- 第一项仅取决于预先选择的概率质量函数 p t p_t pt(在我们的实验中选择为均匀分布)
- 第二项可以从分类器输出向量的第 t t t 和 T + 1 T+1 T+1 个条目中获得。这意味着我们可以计算任何给定图像 x x x相对于任意噪声水平 t t t 下的噪声图像密度 p x t p_{xt} pxt 的似然性。
四、实验
(一)使用两种损失对于实现最佳分类器的重要性
使用不同损失训练的模型达到的MSE、CE和分类准确率:从表格 1 可以明显看出,仅使用CE损失时,MSE很高;而仅使用MSE损失时,CE和分类准确率则很差。一个重要的观察点是,即使在使用CE损失训练时,分类器的准确率也很低。这是使得DRE方法有效的关键前提。具体来说,为了避免密度差问题,分类问题应该足够困难,否则分类器甚至可以在没有学习到正确密度比率的情况下轻松区分类别。

(二)去噪结果、图像质量和负对数似然
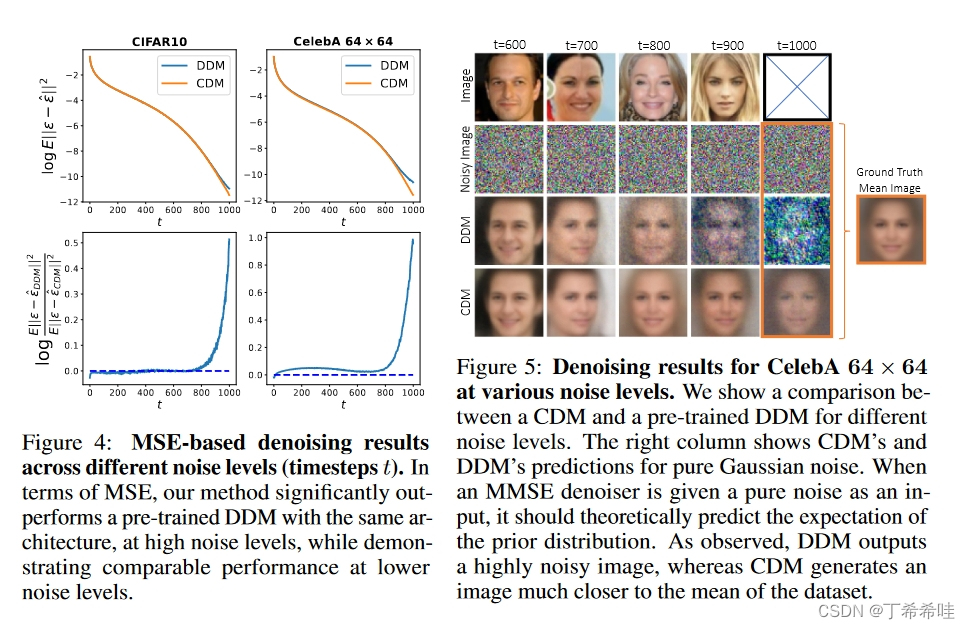
对于图像去噪,CDM 在 MSE 方面超过了高噪声水平下预训练的 DDM,同时在较低噪声水平下实现了可比较的 MSE,如图 4 所示。这些定量结果得到了图 5 中的定性示例的证实,它展示了不同噪声水平下的图像去噪结果。
相关文章:

【论文精读】分类扩散模型:重振密度比估计(Revitalizing Density Ratio Estimation)
文章目录 一、文章概览(一)问题的提出(二)文章工作 二、理论背景(一)密度比估计DRE(二)去噪扩散模型 三、方法(一)推导分类和去噪之间的关系(二&a…...
kubesphere踩过的坑,持续更新....
踩过的坑 The connection to the server lb.kubesphere.local:6443 was refused - did you specify the right host… 另一篇文档中 dashboard 安装 需要在浏览器中输入thisisunsafe,即可进入登录页面 ingress 安装的问题 问题描述: 安装后通过命令 kubectl g…...
做Android开发怎么才能不被淘汰?
多学一项技能,可能就会成为你升职加薪的利器。经常混迹于各复杂业务线的人,才能跳出重复工作、不断踩坑的怪圈。而一个成熟的码农在于技术过关后,更突出其他技能对专业技术的附加值。 毋须讳言的是,35岁以后你的一线coding能力一…...
异步爬虫:aiohttp 异步请求库使用:
使用requests 请求库虽然可以完成爬虫业务,但是对于异步任务来说,它是做不到的, 这时候我们需要借助 aiohttp 异步请求库来完成异步爬虫的编写: 话不多说,直接看示例: 注意:楼主使用的python版…...

代码随想录算法训练营第四十七天|LeetCode123 买卖股票的最佳时机Ⅲ
题1: 指路:123. 买卖股票的最佳时机 III - 力扣(LeetCode) 思路与代码: 买卖股票专题中三者不同的是Ⅰ为只买卖一次,Ⅱ可多次买卖,Ⅲ最多可买卖两次。那么我们将买买卖行为分为五个状态部分(…...
将知乎专栏文章转换为 Markdown 文件保存到本地
一、参考内容 参考知乎文章代码 | 将知乎专栏文章转换为 Markdown 文件保存到本地,利用代码为GitHub:https://github.com/chenluda/zhihu-download。 二、步骤 1.首先安装包flask、flask-cors、markdownify 2. 运行app.py 3.在浏览器中打开链接&…...
【notes2】并发,IO,内存
文章目录 1.线程/协程/异步:并发对应硬件资源是cpu,线程是操作系统如何利用cpu资源的一种抽象2.并发:cpu,线程2.1 可见性:volatile2.2 原子性(读写原子):AtomicInteger/synchronized…...

Python题目
实例 3.1 兔子繁殖问题(斐波那契数列) 兔子从出生后的第三个月开始,每月都会生一对兔子,小兔子成长到第三个月后也会生一对独自。初始有一对兔子,假如兔子都不死,那么计算并输出1-n个月兔子的数量 n int…...

Hive怎么调整优化Tez引擎的查询?在Tez上优化Hive查询的指南
文章目录 在Tez上优化Hive查询的指南调优指南理解Tez中的并行化理解mapper数量理解reducer数量 并发案例1:未指定队列名称案例2:指定队列名称并发的指南/建议 容器复用和预热容器容器复用预热容器 一般Tez调优参数 在Tez上优化Hive查询的指南 在Tez上优…...

关于小程序内嵌H5页面交互的问题?
有木有遇到?有木有遇到。 小程序内嵌了H5,然后H5某个按钮,需要打开小程序某个页面进行信息完善或登记,登记后要返回H5页面,而H5页面要动态显示刚才在小程序页面登记的信息。 操作流程是这样: 方案1&#…...

Linux下手动查杀木马与Rootkit的实战指南
模拟木马程序的自动运行 黑客可以通过多种方式让木马程序自动运行,包括: 计划任务 (crontab):通过设置定时任务来周期性地执行木马脚本。开机启动:在系统的启动脚本中添加木马程序,确保系统启动时木马也随之运行。替…...
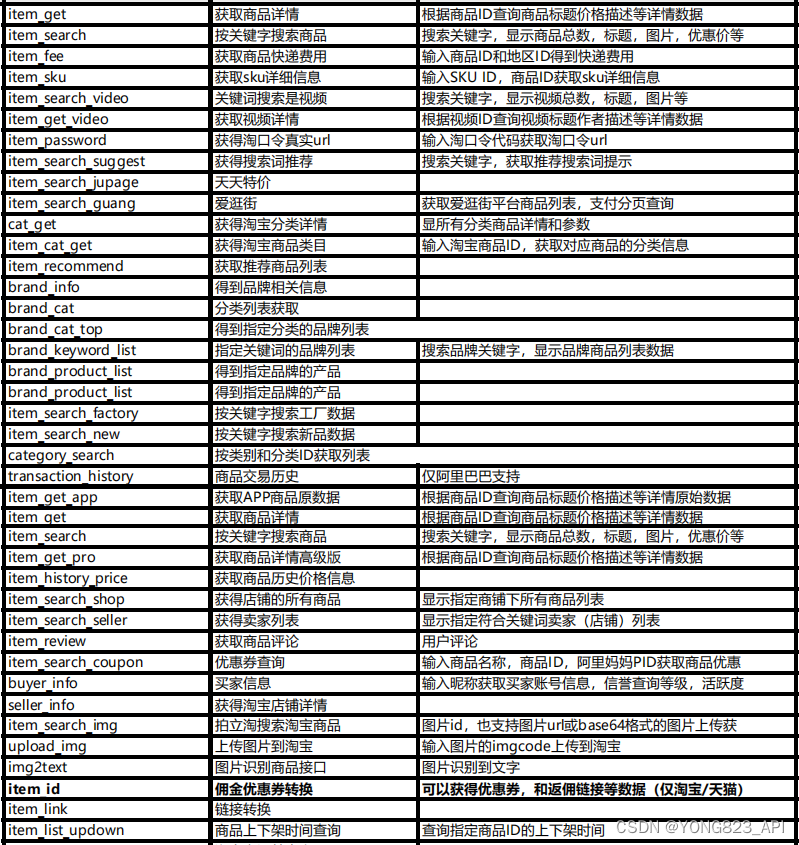
电商爬虫API的定制开发:满足个性化需求的解决方案
一、引言 随着电子商务的蓬勃发展,电商数据成为了企业决策的重要依据。然而,电商数据的获取并非易事,特别是对于拥有个性化需求的企业来说,更是面临诸多挑战。为了满足这些个性化需求,电商爬虫API的定制开发成为了解决…...

nuc马原复习资料
哲学:世界观的理论形态,或者说是系统化、理论化的世界观;世界观和方法论的统一。马克思主义哲学:辩证唯物主义和历史唯物主义,关于自然。社会和思维发展的普遍规律的学说,无产阶级世界观的理论体系。世界观…...

Node.js是什么(基础篇)
前言 Node.js是一个基于Chrome V8 JavaScript引擎的开源、跨平台JavaScript运行时环境,主要用于开发服务器端应用程序。它的特点是非阻塞I/O模型,使其在处理高并发请求时表现出色。 一、Node JS到底是什么 1、Node JS是什么 Node.js不是一种独立的编程…...

淘客返利平台的微服务架构实现
淘客返利平台的微服务架构实现 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨淘客返利平台的微服务架构设计与实现,旨在提高系统的灵…...

【database1】mysql:DDL/DML/DQL,外键约束/多表/子查询,事务/连接池
文章目录 1.mysql安装:存储:集合(内存:临时),IO流(硬盘:持久化)1.1 服务端:双击mysql-installer-community-5.6.22.0.msi1.2 客户端:命令行输入my…...

模拟木马程序自动运行:Linux下的隐蔽攻击技术
模拟木马程序自动运行:Linux下的隐蔽攻击技术 在网络安全领域,木马程序是一种常见的恶意软件,它能够悄无声息地在受害者的系统中建立后门,为攻击者提供远程访问权限。本文将探讨攻击者如何在Linux系统中模拟木马程序的自动运行&a…...

vuex的配置主要内容
1、state 作用:负责存储数据; 2、getters 作用:state计算属性(有缓存); 3、mutaions 作用:负责同步更新state数据 mutaions是唯一可以修改state数据的方式; 4、actions 作用:负责异步操作&a…...
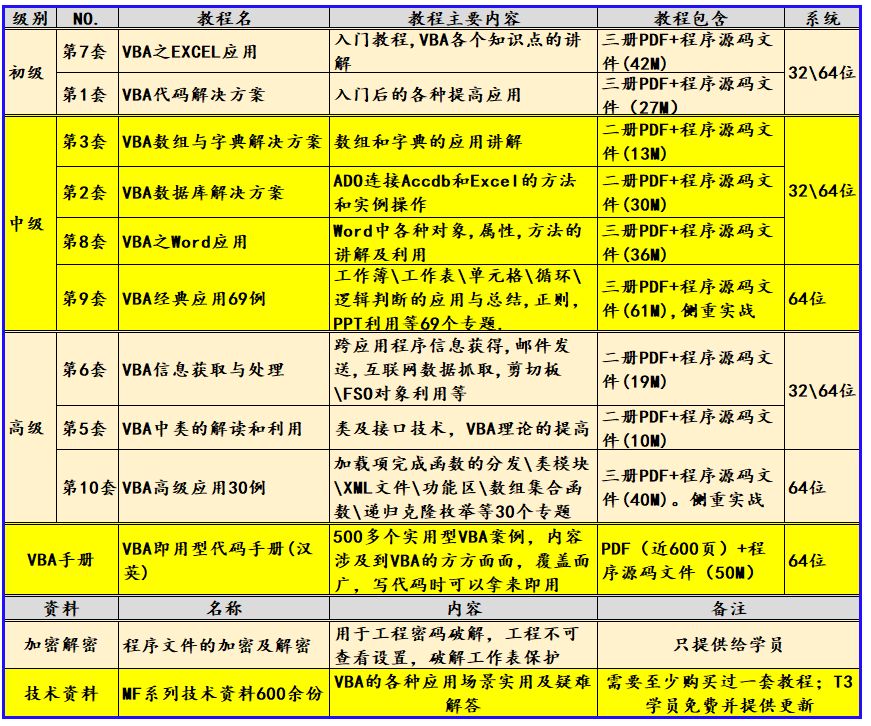
VBA技术资料MF164:列出文件夹中的所有文件和创建日期
我给VBA的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。“VBA语言専攻”提供的教程一共九套,分为初级、中级、高级三大部分,教程是对VBA的系统讲解&#…...
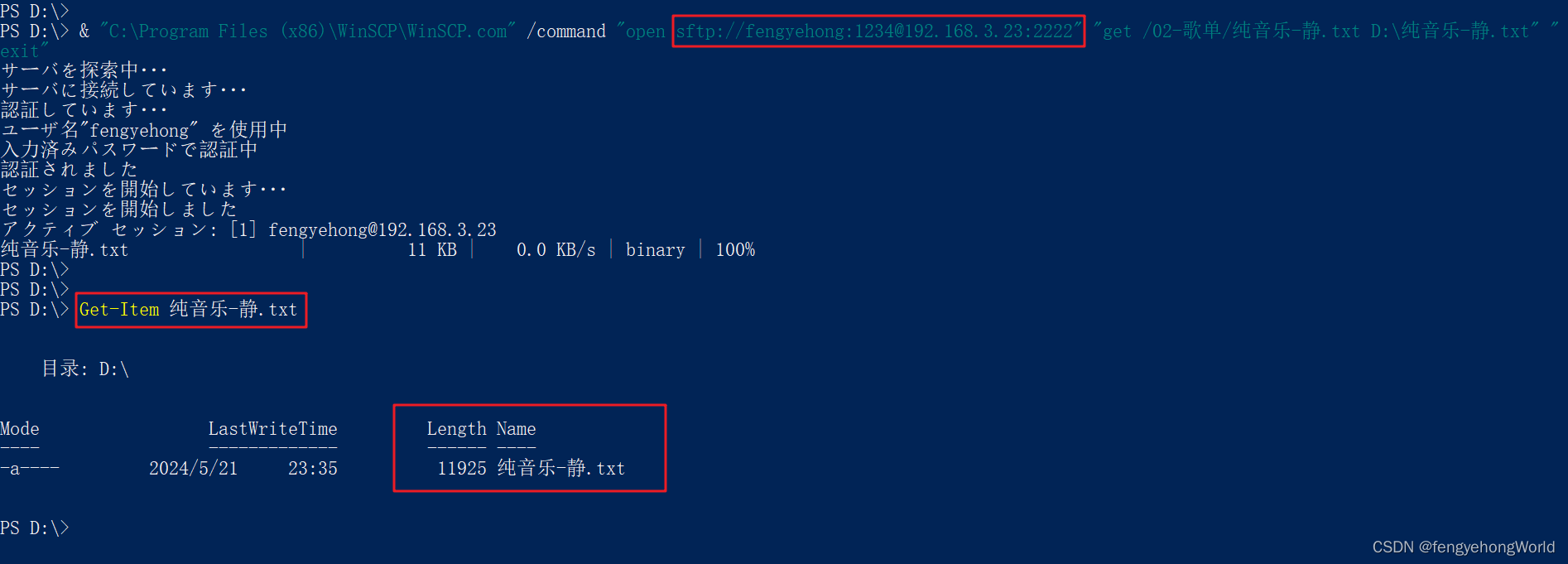
linux 简单使用 sftp 和 lftp命令
目录 一. 环境准备二. sftp命令连接到SFTP服务器三. lftp命令3.1 连接FTP和SFTP服务器3.2 将文件从sftp服务器下载到本地指定目录 四. 通过WinSCP命令行从SFTP服务器获取文件到Windows 一. 环境准备 ⏹在安卓手机上下载个MiXplorer,用作SFTP和FTP服务器 官网: htt…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...
