贪心算法练习题(2024/6/18)
什么是贪心
贪心的本质是选择每一阶段的局部最优,从而达到全局最优。
贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
1分发饼干
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
示例 1:
输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。 虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。 所以你应该输出1。
示例 2:
输入: g = [1,2], s = [1,2,3] 输出: 2 解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。 你拥有的饼干数量和尺寸都足以让所有孩子满足。 所以你应该输出2.
提示:
1 <= g.length <= 3 * 1040 <= s.length <= 3 * 1041 <= g[i], s[j] <= 231 - 1
思路:
-
排序: 首先,将孩子的胃口数组
g和饼干的大小数组s分别按从小到大排序。这样做是为了能够从最小的胃口和最小的饼干开始匹配,以尽可能满足更多的孩子。 -
贪心策略: 使用贪心算法的核心思想,从胃口最大的孩子开始,尝试给他们分配能满足他们胃口的最小饼干。这里的贪心选择是每次都选择当前能够满足的最小饼干,以期望最终能够满足尽可能多的孩子。
-
实现细节:
- 使用
index表示当前可用的饼干数组的最后一个元素的下标。 - 从最大胃口的孩子开始向最小胃口的孩子遍历,尝试找到合适的饼干分配。
- 如果当前的饼干能够满足当前孩子的胃口,则结果
result加一,并将index减一,表示使用了这个饼干。 - 如果当前的饼干不能满足当前孩子的胃口,则继续向前尝试下一个更大的饼干,直到找到合适的或者饼干用完。
- 使用
-
返回结果: 最终返回
result,即能够满足的孩子的数量。
代码:
class Solution {
public:int findContentChildren(vector<int>& g, vector<int>& s) {// 将孩子数组和饼干数组按照从小到大排序sort(g.begin(), g.end()); // 按照孩子的胃口排序sort(s.begin(), s.end()); // 按照饼干的大小排序int index = s.size() - 1; // 饼干数组的下标int result = 0; // 结果,能满足孩子的数量// 从胃口最大的孩子开始匹配饼干for (int i = g.size() - 1; i >= 0; i--) { // 遍历胃口// 如果还有饼干可用且当前饼干满足当前孩子的胃口if (index >= 0 && s[index] >= g[i]) { // 遍历饼干result++; // 满足一个孩子index--; // 使用了一个饼干,下标减一}}return result; // 返回满足孩子的数量}
};2摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3) 。
示例 2:
输入:nums = [1,17,5,10,13,15,10,5,16,8] 输出:7 解释:这个序列包含几个长度为 7 摆动序列。 其中一个是 [1, 17, 10, 13, 10, 16, 8] ,各元素之间的差值为 (16, -7, 3, -3, 6, -8) 。
示例 3:
输入:nums = [1,2,3,4,5,6,7,8,9] 输出:2
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
思路:
代码:
局部最优:删除单调坡度上的节点(不包括单调坡度两端的节点),那么这个坡度就可以有两个局部峰值。
整体最优:整个序列有最多的局部峰值,从而达到最长摆动序列。只需要统计数组的峰值数量就可以了。
-
初始化:
curDiff初始化为0,表示当前一对相邻元素的差值。preDiff也初始化为0,表示前一对相邻元素的差值。result初始化为1,因为序列默认至少有一个峰值。
-
处理边界情况:
- 如果数组
nums的大小<= 1,直接返回nums.size(),因为这种情况下不可能形成长度大于1的摆动序列。
- 如果数组
-
遍历数组:
- 循环遍历数组
nums,从第一个元素到倒数第二个元素 (i < nums.size() - 1)。
- 循环遍历数组
-
计算差值:
- 计算
curDiff为nums[i + 1] - nums[i],即当前两个相邻元素的差值。
- 计算
-
检测峰值和谷值:
- 当
preDiff <= 0 && curDiff > 0或者preDiff >= 0 && curDiff < 0时,表示出现了摆动的峰值或者谷值。 - 在这些情况下,增加
result的计数,因为它们是摆动序列的关键点。
- 当
-
返回结果:
- 最终返回
result,即最长摆动子序列的长度。
- 最终返回
class Solution {
public:int wiggleMaxLength(vector<int>& nums) {if (nums.size() <= 1) return nums.size();int curDiff = 0; // 当前一对差值int preDiff = 0; // 前一对差值int result = 1; // 记录峰值个数,序列默认序列最右边有一个峰值for (int i = 0; i < nums.size() - 1; i++) {curDiff = nums[i + 1] - nums[i];// 出现峰值if ((preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)) {result++;preDiff = curDiff; // 注意这里,只在摆动变化的时候更新prediff}}return result;}
};3最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
示例 2:
输入:nums = [1] 输出:1
示例 3:
输入:nums = [5,4,-1,7,8] 输出:23
提示:
1 <= nums.length <= 105-104 <= nums[i] <= 104
思路:
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”
局部最优的情况下,并记录最大的“连续和”,可以推出全局最优。
该贪心算法实现的思路是在遍历数组的过程中,持续累积子数组的元素和,同时不断更新最大子数组之和。如果当前累积和变为负数,就重新开始计算子数组和,以期获得更大的子数组和。
代码:
class Solution {
public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN; // 初始化最大和为负无穷int count = 0; // 当前累积和for (int i = 0; i < nums.size(); i++) {count += nums[i]; // 累加当前元素到当前和if (count > result) {result = count; // 更新最大和为当前和}if (count <= 0) {count = 0; // 如果当前和小于等于0,则重新开始计算累积和}}return result; // 返回最大和}
};相关文章:
)
贪心算法练习题(2024/6/18)
什么是贪心 贪心的本质是选择每一阶段的局部最优,从而达到全局最优。 贪心算法一般分为如下四步: 将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解 1分发饼干 假设你是一位很棒的家长,…...

4.1 四个子空间的正交性
一、四个子空间的正交性 如果两个向量的点积为零,则两个向量正交: v ⋅ w v T w 0 \boldsymbol v\cdot\boldsymbol w\boldsymbol v^T\boldsymbol w0 v⋅wvTw0。本章着眼于正交子空间、正交基和正交矩阵。两个子空间的中的向量,一组基中的向…...
RabbitMQ实践——使用WebFlux响应式方式实时返回队列中消息
大纲 Pom.xml监听队列实时返回消息测试完整代码工程代码 在之前的案例中,我们在管理后台收发消息都是通过短连接的形式。本文我们将探索对队列中消息的实时读取,并通过流式数据返回给客户端。 webflux是反应式Web框架,客户端可以通过一个长连…...

SpringBoot前后端传递数据时常用的JSON格式数据是什么?【讲解JSON概念、语法、以及Java对象互转】
SpringBoot前后端传递数据时常用的JSON格式数据是什么? JSON概念JSON语法JSON的两种结构:JSON字符串和Java对象互转:objectMapper.writeValueAsString(person);objectMapper.readValue(jsonStr,Person.class); 在SpringMVC框架中,…...

mysql学习——SQL中的DQL和DCL
SQL中的DQL和DCL DQL基本查询条件查询聚合函数分组查询排序查询分页查询 DCL管理用户权限控制 学习黑马MySQL课程,记录笔记,用于复习。 DQL DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据库中表的记…...
windows系统上nginx搭建文件共享
1、下载windows版nginx 下载地址 2、配置nginx 编辑nginx.conf配置文件 在http模块下添加这个参数 underscores_in_headers on;#修改location内容,共享哪个文件夹,就写哪个文件夹,最后一定要跟上/,否则无法访问 location / {…...
星闪指向遥控,做家电交互的破壁人
“面壁者罗辑,我是你的破壁人。” 科幻小说《三体》中,当人类的基础科学被三体人封锁,变得停步不前,人类启动了自救的面壁计划,通过一次又一次破壁,找到战胜三体人的办法。 现实中,有一点已经成…...
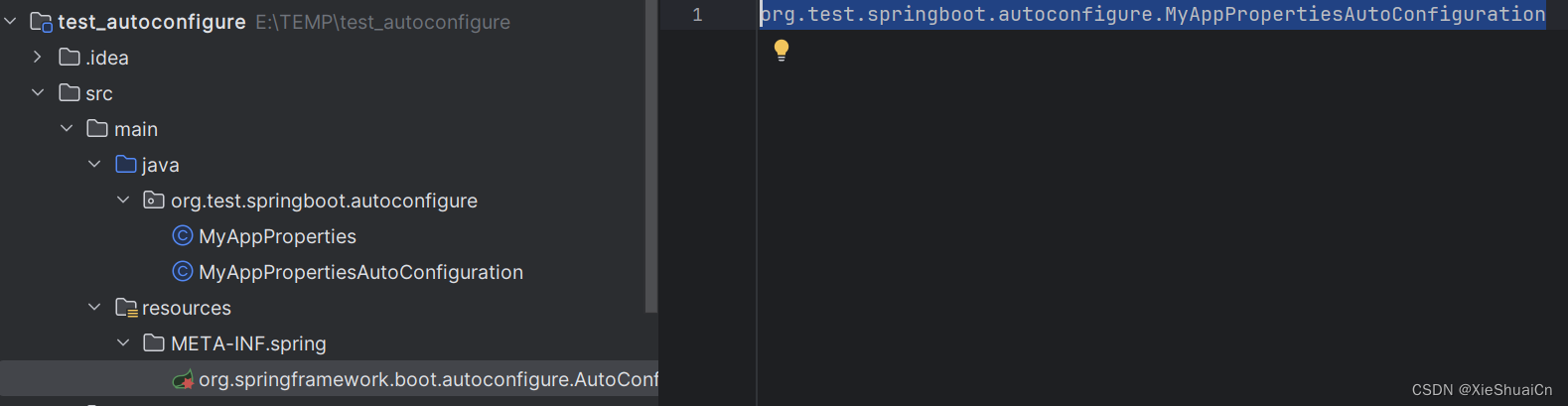
SpringBoot使用AutoConfigure实现依赖库自动导入配置
我们知道导入配置有两种,一种是Value,一种是ConfigurationProperties,将对应的类标记为Component即可导入。但是被注解标识的类创建Bean有一个前提,只对启动类所在的包路径下的所有带有Component等注解的类才会创建Bean。如果我们…...
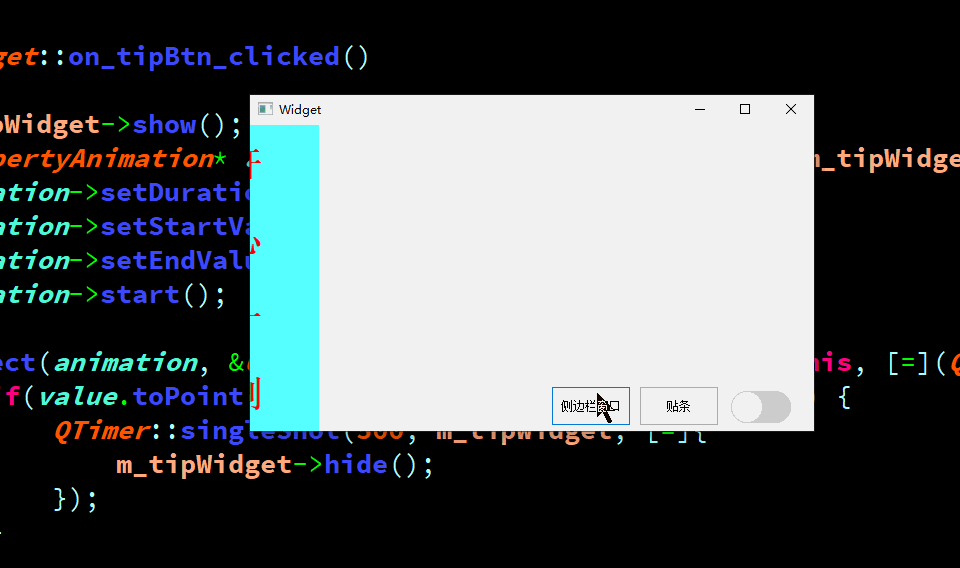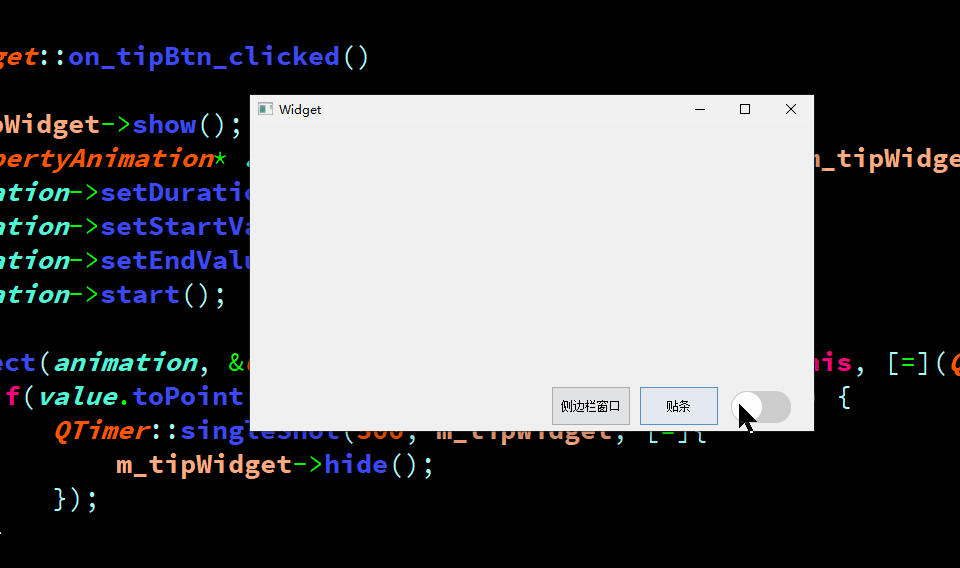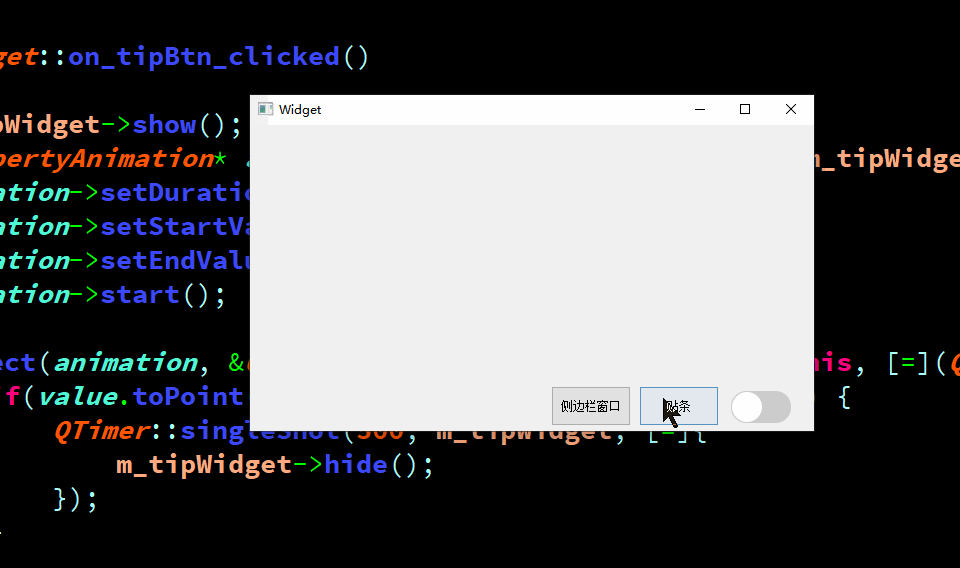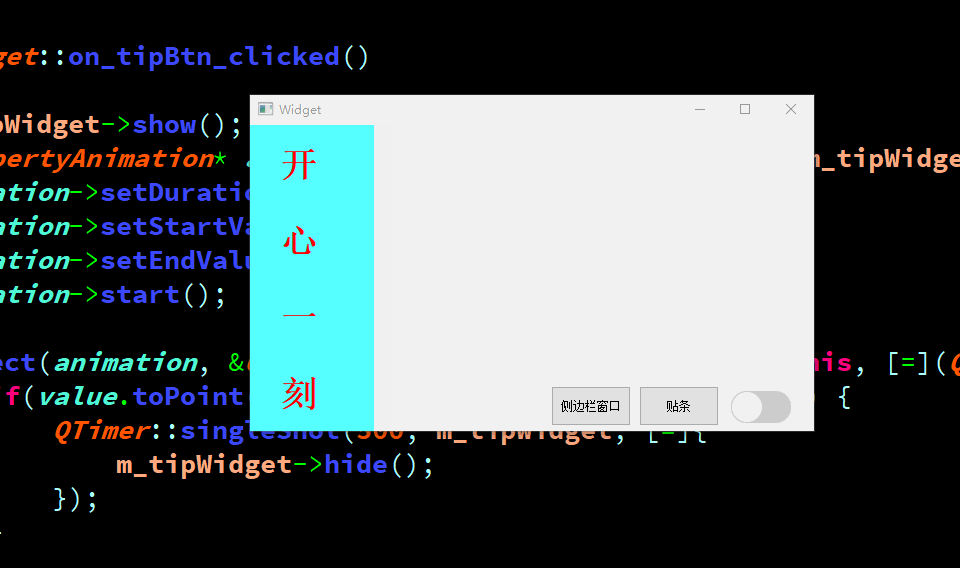
QT中利用动画弄一个侧边栏窗口,以及贴条效果
1、效果 2、关键代码 void Widget::on_sliderBtn_clicked() {m_sliderWidget->show();QPropertyAnimation* animation = new QPropertyAnimation(m...

win10免安装配置MySQL8.4.0
注:此教程基于win10 22H2 版本 1、下载最新版本MySQL压缩包 下载链接:MySQL官网下载地址 点击第二行的 ZIP Archive 后面的Download(当前时间2024-06-19最新版本是8.4.0) 2、解压并添加配置文件 下载完毕后,解压缩…...
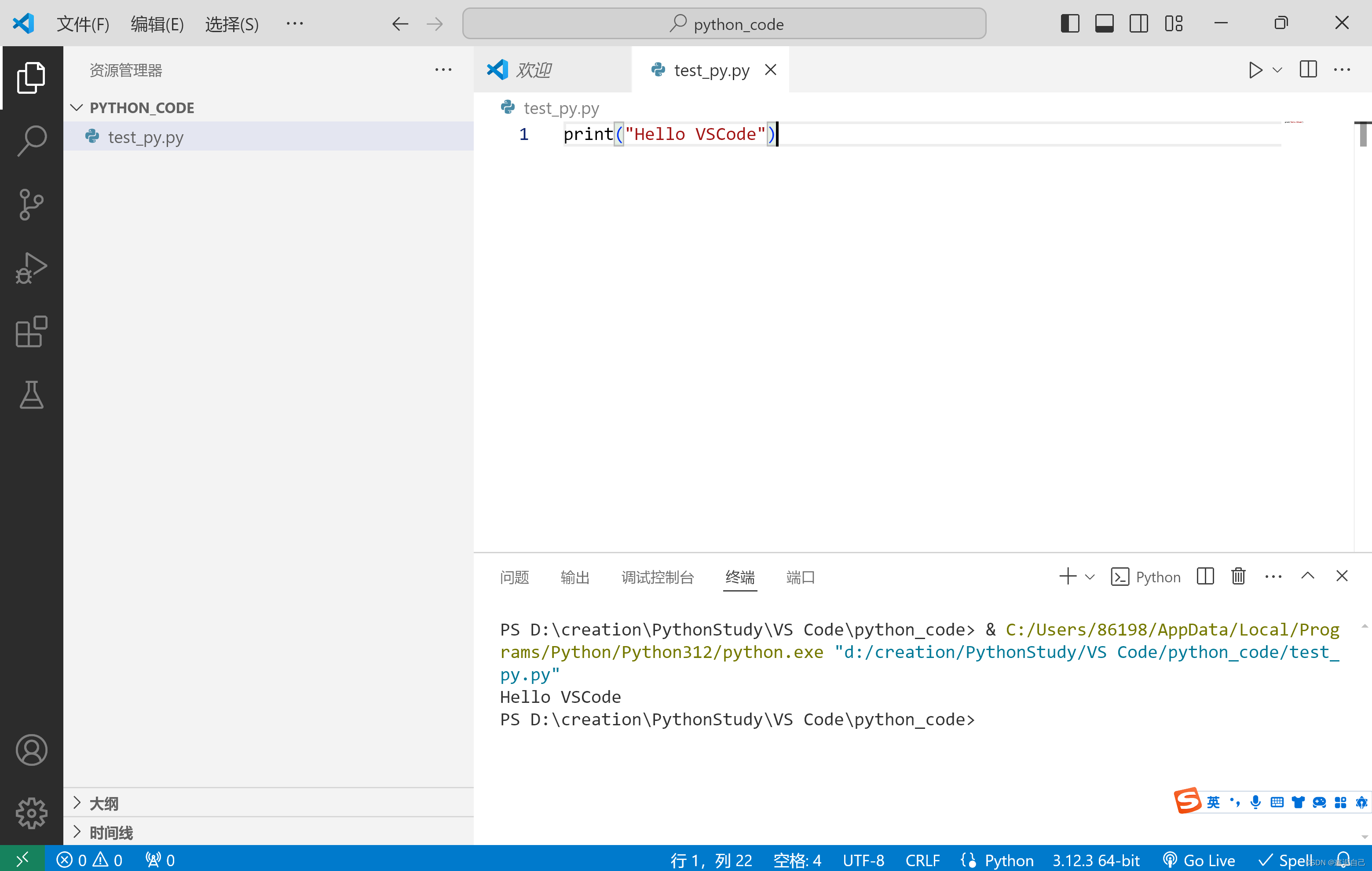
VS Code安装及环境配置(超详细)
VS Code简介 Visual Studio Code(简称 VS Code )是 Microsoft 于2015年4月发布的一款代码编辑器,以界面简洁、轻量著称。 它是一款免费开源的现代化轻量级代码编辑器,支持几乎所有主流开发语言的语法高亮、智能代码补全、自定义…...

shell脚本通过解析日志使用串口开关屏知识点整理
#!/bin/bash #logPath 写日志的存放路径 #logPath/home/workspace/tvs/trainborne logPath/home/firefly tmpFile$$ function getLogName() { #echo "$logPath/LCDController_"date "%Y%m%d000000.log" echo "LCDController_20240424000000.log&quo…...

速盾:视频cdn和网站cdn的相同点与不同点
CDN(Content Delivery Network)是一种分布式网络架构,旨在为用户提供高效、高质量的内容传送服务。CDN主要通过将内容分发到全球各地的边缘节点,并根据用户的地理位置选择最近的节点来提供内容,从而加速内容的传输并降…...

37.自定义协议
自定义协议要素 1.魔数:用来第一时间判定是否是无效数据包。 2.版本号:主持协议升级。 3.序列化算法:消息正文到底采用那种序列化方式,可以由此扩展,例如:json,protobuf(google的序列化算法,基于二进制,虽然可读性不好,但是字节数占用更少),hessian(基于二进制)…...
【React Native】measureInWindow在安卓上无法正确获取View在屏幕上的布局信息
问题描述: 在React Native中,我们可以使用measureInWindow的方式去获取一个View在屏幕中的位置信息: 下面这个Demo中,我们写了一个页面HomePage和一个列表项组件ListItemA,我们期望每过5s监测一次列表中每一项在屏幕中…...

C++ 教程 - 04 类的使用
文章目录 类的定义类定义案例构造函数 类的定义 C 在 C 语言的基础上增加面向对象编程,类是用于指定对象的形式,是一种用户自定义的数据类型,封装了数据和函数。类可以被看作是一种模板,可以用来创建具有相同属性和行为的多个对象…...

excel按模板文件导出多个文件并压缩为ZIP格式返回前端
思路:先准备好模板文件和与之对应的实体类,数据库数据等,还是之前思路,根据查出的数据,填充模板文件,生成一个临时文件,最后将这些个临时文件打包为zip返回前端,并将多个临时文件删除…...

自动驾驶仿真测试用例表格示例 ACC ELK FCW
自动驾驶仿真测试用例表格示例 测试用例概览 本测试用例表格涵盖了自动驾驶系统中多个关键功能和场景的测试,旨在确保系统在不同条件下的表现和稳定性。 用例编号测试项目测试描述预期结果实际结果通过/失败TC-001ACC功能测试在高速公路上启用ACC,测试车…...

数组 (java)
文章目录 一维数组静态初始化动态初始化 二维数组静态初始化动态初始化 数组参数传递可变参数关于 main 方法的形参 argsArray 工具类sort 中的 comparable 和 comparatorcomparator 比较器排序comparable 自然排序 一维数组 线性结构 静态初始化 第一种:int[] a…...
时序预测 | Matlab基于Transformer多变量时间序列多步预测
目录 效果一览基本介绍程序设计参考资料 效果一览 基本介绍 1.Matlab基于Transformer多变量时间序列多步预测; 2.多变量时间序列数据集(负荷数据集),采用前96个时刻预测的特征和负荷数据预测未来96个时刻的负荷数据; 3…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

Spring是如何解决Bean的循环依赖:三级缓存机制
1、什么是 Bean 的循环依赖 在 Spring框架中,Bean 的循环依赖是指多个 Bean 之间互相持有对方引用,形成闭环依赖关系的现象。 多个 Bean 的依赖关系构成环形链路,例如: 双向依赖:Bean A 依赖 Bean B,同时 Bean B 也依赖 Bean A(A↔B)。链条循环: Bean A → Bean…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

人工智能 - 在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型
在Dify、Coze、n8n、FastGPT和RAGFlow之间做出技术选型。这些平台各有侧重,适用场景差异显著。下面我将从核心功能定位、典型应用场景、真实体验痛点、选型决策关键点进行拆解,并提供具体场景下的推荐方案。 一、核心功能定位速览 平台核心定位技术栈亮…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...
