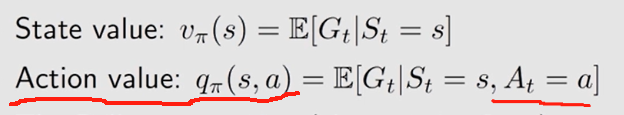▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch5 蒙特卡洛方法【model-based ——> model-free】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍
- 1、视频 + 学堂在线 习题
- 2、 过 电子书 是否遗漏 【下载:本章 PDF GitHub 页面链接 】 【第二轮 才整理的,忘光了。。。又看了一遍视频】
- 3、 过 MOOC 习题
- 看 PDF 迷迷糊糊, 恍恍惚惚。
学堂在线 课程页面链接
中国大学MOOC 课程页面链接
B 站 视频链接
PPT和书籍下载网址: 【GitHub链接】
文章目录
- 5.1 蒙特卡洛估计 的基本思想
- 大数定理
- —— 3 个 基于蒙特卡洛 的强化学习 算法
- 5. 2 MC Basic
- 5.3 MC Exploring Starts
- 5.4 MC ε-Greedy:无需 exploring starts
- 5.5 ε − ~~\varepsilon- ε− greedy 策略的探索与利用

上次课程 model-based 【值迭代、策略迭代。动态规划】基于系统模型找最优策略
本次课程 第一次介绍 model-free 方法
策略迭代方法 是这次课的基础 : 把 策略迭代 中基于模型的部分 替换成 不需要模型的。
动态规划: 值迭代、策略迭代 【model-based】
基于模型的强化学习方法: 用数据 估计出一个模型,根据这个模型进行强化学习。

找最优策略: 要么有模型, 要么有数据
强化学习中的 “数据” 通常是指智能体与环境的交互经验。
5.1 蒙特卡洛估计 的基本思想
P1
如何在没有模型的情况下 估计一些量? ——> 蒙特卡洛估计
针对 硬币投掷 问题,期望计算
方法一: 当 概率模型已知, 基于概率模型 进行计算。
- 有些问题对应的精确概率分布无法知晓

方法二: 蒙特卡洛思想【多次投掷硬币,求平均值】

大数定律:大量样本的平均值 接近 期望值。

如果概率分布未知,那么我们可以多次抛硬币并记录采样结果 { x i } i = 1 n \{x_i\}_{i=1}^n {xi}i=1n 通过计算样本的平均值,我们可以得到均值的估计。
随着样本数量的增加,估计的均值越来越准确。
用于均值估计的样本必须是独立且同分布的 (i.i.d. 或 iid)。
否则,如果采样值相关,则可能无法正确估计期望值。
一个极端的情况是所有的采样值都和第一个相同,不管第一个是什么。在这种情况下,无论我们使用多少个样本,样本的平均值总是等于第一个样本。
大数定理
对于随机变量 X X X, 假设 { x j } j = 1 N \{x_j\}_{j=1}^N {xj}j=1N 是独立同分布抽样。其中 样本均值 x ˉ = 1 N ∑ j = 1 N x j \bar{x}=\frac{1}{N}\sum\limits_{j=1}^Nx_j xˉ=N1j=1∑Nxj。则
1、 x ˉ \bar{x} xˉ 是 E [ X ] \mathbb{E}[X] E[X] 的无偏估计: E [ x ˉ ] = E [ X ] \mathbb{E}[\bar{x}]=\mathbb{E}[X] E[xˉ]=E[X]
2、当 N → ∞ N \to \infty N→∞, 方差趋向 0。 V a r [ x ˉ ] = 1 N V a r [ X ] Var [\bar{x}]= \frac{1}{N}Var[X] Var[xˉ]=N1Var[X]
样本均值的 期望 等于总体的期望
样本均值的 方差 等于总体方差的 1 N \frac{1}{N} N1
证明: 电子书 补充 P90
E [ x ˉ ] = E [ 1 N ∑ i = 1 N x i ] = 1 N ∑ i = 1 N E [ x i ] = 同分布 E [ X ] \mathbb{E}[\bar{x}] = \mathbb{E}[\frac{1}{N}\sum_{i=1}^Nx_i] =\frac{1}{N}\sum_{i=1}^N\mathbb{E}[x_i]\xlongequal{同分布}\mathbb{E}[X] E[xˉ]=E[N1i=1∑Nxi]=N1i=1∑NE[xi]同分布E[X]
同分布,则 E [ x i ] = E [ X ] \mathbb E[x_i]=\mathbb E[X] E[xi]=E[X]
V a r [ x ˉ ] = V a r [ 1 N ∑ i = 1 N x i ] = 独立 1 N 2 ∑ i = 1 N V a r [ x i ] = 1 N 2 ⋅ N ⋅ V a r [ X ] = 同分布 1 N V a r [ X ] Var[\bar{x}] = Var[\frac{1}{N}\sum_{i=1}^Nx_i] \xlongequal{独立}\frac{1}{N^2}\sum_{i=1}^NVar[x_i]=\frac{1}{N^2}· N·Var[X]\xlongequal{同分布}\frac{1}{N}Var[X] Var[xˉ]=Var[N1i=1∑Nxi]独立N21i=1∑NVar[xi]=N21⋅N⋅Var[X]同分布N1Var[X]

蒙特卡洛估计: 重复随机抽样 近似
- 无需模型
状态值 和 动作值 为随机变量期望
蒙特卡洛估计是指依靠重复随机抽样来解决近似问题的一大类技术。
为什么我们关心蒙特卡洛估计?因为它不需要模型!
为什么我们关心均值估计?因为 状态值 和 动作值 被定义为随机变量的期望!
为什么关心均值估计问题?
因为 状态值 和 动作值 都被定义为 折扣回报 的均值。
估计 状态值 或 动作值 实际上是一个均值估计问题。
- v π ( s ) = E [ G t ∣ S t = s ] v_\pi(s)=\mathbb{E}[G_t|S_t=s] vπ(s)=E[Gt∣St=s]
- q π ( s , a ) = E [ G t ∣ S t = s , A t = a ] q_\pi(s,a)=\mathbb{E}[G_t|S_t=s, A_t=a] qπ(s,a)=E[Gt∣St=s,At=a]
—— 3 个 基于蒙特卡洛 的强化学习 算法
MC Basic、MC Exploring Starts、MC ε-Greedy
5. 2 MC Basic
P2 - P3
如何 将 策略迭代算法 转成 model-free 方法?
蒙特卡洛均值估计
策略迭代算法 在 一次迭代 中的两步:
策略评估: v π k = r π k + γ P π k v π k v_{\pi_k} = r_{\pi_k}+\gamma P_{\pi_k}v_{\pi_k} vπk=rπk+γPπkvπk
策略改进: π k + 1 = arg max π ( r π + γ P π v π k ) \pi_{k+1}=\arg\max\limits_{\pi}(r_\pi + \gamma P_\pi v_{\pi_k}) πk+1=argπmax(rπ+γPπvπk)
————
其中
π k + 1 ( s ) = arg max π ∑ a π ( a ∣ s ) [ ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π k ( s ′ ) ] = arg max π ∑ a π ( a ∣ s ) q π k ( s , a ) , s ∈ S \begin{align*}\pi_{k+1}(s) &=\arg\max_\pi\sum_a\pi(a|s)\Big[\sum_rp(r|s, a)r+\gamma\sum_{s^{\prime}} p(s^{\prime}|s, a)v_{\pi_k}(s^{\prime})\Big]\\ &= \arg \max_\pi \sum_a \pi(a|s) q_{\pi_k}(s, a), ~~ s \in \mathcal{S}\end{align*} πk+1(s)=argπmaxa∑π(a∣s)[r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπk(s′)]=argπmaxa∑π(a∣s)qπk(s,a), s∈S
两个步骤中, 动作值 是核心:第一步计算的 状态值 是为了 第二步 中动作值的计算, 且第二步中 新策略 是基于 动作值 确定
选择最大的 q π k ( s , a ) q_{\pi_k}(s, a) qπk(s,a),得到新的策略。
那么关键在于如何计算 q π k ( s , a ) q_{\pi_k}(s, a) qπk(s,a) ?
修改 动作值 的求解公式:
方法一: model-based 策略迭代算法。
- 先通过求解 贝尔曼公式 计算 状态值 v π k v_{\pi_k} vπk,再通过下式计算 动作值。
- q π k ( s , a ) = ∑ r p ( r ∣ s , a ) r + γ ∑ s ′ p ( s ′ ∣ s , a ) v π k ( s ′ ) q_{\pi_k}(s, a)=\sum\limits_rp(r|s, a)r+\gamma \sum\limits_{s^{\prime}}p(s^{\prime}|s, a)v_{\pi_k}(s^{\prime}) qπk(s,a)=r∑p(r∣s,a)r+γs′∑p(s′∣s,a)vπk(s′)
- 需要模型 p ( r ∣ s , a ) p(r|s, a) p(r∣s,a) 和 p ( s ′ ∣ s , a ) p(s^{\prime}|s, a) p(s′∣s,a) 已知。 奖励 和 状态转换 的概率分布
~公式二: model-free 无需模型,基于数据或经验 ✔
- q π k ( s , a ) = E [ G t ∣ S t = s , A t = a ] ≈ 1 n ∑ i = 1 n g π k ( i ) ( s , a ) q_{\pi_k}(s, a)=\mathbb{E}[G_t|S_t=s, A_t=a]\textcolor{blue}{\approx\frac{1}{n}\sum\limits_{i=1}^ng_{\pi_k}^{(i)}(s, a)}~~~~~ qπk(s,a)=E[Gt∣St=s,At=a]≈n1i=1∑ngπk(i)(s,a) 从定义出发
G t G_t Gt: 折扣回报

没有模型时, 依赖数据。
数据在统计或概率里叫 sample, 在强化学习里称为 experience经验。
求解流程:

第 k k k 次迭代:
1、策略评估:对所有 ( s , a ) (s, a) (s,a) , 求 q π k q_{\pi_k} qπk
从 ( s , a ) (s, a) (s,a) 出发, 得到 很多 episodes[回合],对所有 episode 的 return 求平均。
- 策略迭代: 计算 状态值 ——> 根据系统模型计算 动作值 。【需要 奖励 和 状态转移概率 已知】
- MC Basic: 直接通过数据得到 q π k q_{\pi_k} qπk。
2、策略改进: 将 动作 改成 最大 q π k q_{\pi_k} qπk 对应的动作。
算法描述:

无模型算法 直接估计 动作值。
否则,如果估计状态值,我们仍然需要使用系统模型从这些状态值计算动作值

——————
小结:
MC Basic 是 策略迭代算法 的变形
MC Basic 有助于揭示 基于MC 的无模型 RL 的核心思想,但由于效率低,并不实用。
MC Basic 估计的是 动作值 而不是 状态值。
- 状态值 无法直接用于 改进策略,当系统模型不可获得,应直接估计 动作值。
5.2.3 例子:


针对 s 1 s_1 s1 计算 5 个动作的。
环境 和 策略 均确定, 采样 一次 即可



1、从 ( s 1 , a 1 ) (s_1, a_1) (s1,a1) 开始。上移
episode: s 1 → a 1 s 1 → a 1 s 1 → a 1 ⋯ s_1\xrightarrow{a_1}s_1\textcolor{blue}{\xrightarrow{a_1}s_1\xrightarrow{a_1}\cdots} s1a1s1a1s1a1⋯
q π 0 ( s 1 , a 1 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + ⋯ = ( − 1 ) × 1 × ( 1 − γ ( n + 2 ) ) 1 − γ = − 1 1 − γ q_{\pi_0}(s_1, a_1)=-1+\gamma (-1)+\gamma^2(-1)+\cdots=(-1)\times\frac{1\times(1-\gamma^{(n+2)})}{1-\gamma}=\frac{-1}{1-\gamma} qπ0(s1,a1)=−1+γ(−1)+γ2(−1)+⋯=(−1)×1−γ1×(1−γ(n+2))=1−γ−1
~
2、从 ( s 1 , a 2 ) (s_1, a_2) (s1,a2) 开始。右移
episode: s 1 → a 2 s 2 → a 3 s 5 → a 3 s 8 → a 2 s 9 → a 5 s 9 → a 5 s 9 ⋯ s_1\xrightarrow{a_2}s_2\xrightarrow{a_3}s_5\xrightarrow{a_3}s_8\xrightarrow{a_2}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\cdots s1a2s2a3s5a3s8a2s9a5s9a5s9⋯
q π 0 ( s 1 , a 2 ) = 0 + γ 0 + γ 2 0 + γ 3 1 + γ 4 1 + γ 5 1 + ⋯ = γ 3 1 − γ q_{\pi_0}(s_1, a_2)=0+\gamma0+\gamma^20+\gamma^31+\gamma^41+\gamma^51+\cdots=\frac{\gamma^3}{1-\gamma}~~ qπ0(s1,a2)=0+γ0+γ20+γ31+γ41+γ51+⋯=1−γγ3 ✔
~
3、从 ( s 1 , a 3 ) (s_1, a_3) (s1,a3) 开始。下移
episode: s 1 → a 3 s 4 → a 2 s 5 → a 3 s 8 → a 2 s 9 → a 5 s 9 → a 5 s 9 ⋯ s_1\xrightarrow{a_3}s_4\xrightarrow{a_2}s_5\xrightarrow{a_3}s_8\xrightarrow{a_2}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\cdots s1a3s4a2s5a3s8a2s9a5s9a5s9⋯
q π 0 ( s 1 , a 3 ) = 0 + γ 0 + γ 2 0 + γ 3 1 + γ 4 1 + γ 5 1 + ⋯ = γ 3 1 − γ q_{\pi_0}(s_1, a_3)=0+\gamma0+\gamma^20+\gamma^31+\gamma^41+\gamma^51+\cdots=\frac{\gamma^3}{1-\gamma}~~ qπ0(s1,a3)=0+γ0+γ20+γ31+γ41+γ51+⋯=1−γγ3 ✔
~
4、从 ( s 1 , a 4 ) (s_1, a_4) (s1,a4) 开始。左移
episode: s 1 → a 4 s 1 → a 1 s 1 → a 1 ⋯ s_1\xrightarrow{a_4}s_1\textcolor{blue}{\xrightarrow{a_1}s_1\xrightarrow{a_1}\cdots} s1a4s1a1s1a1⋯
q π 0 ( s 1 , a 4 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + ⋯ = ( − 1 ) × 1 × ( 1 − γ ( n + 2 ) ) 1 − γ = − 1 1 − γ q_{\pi_0}(s_1, a_4)=-1+\gamma (-1)+\gamma^2(-1)+\cdots=(-1)\times\frac{1\times(1-\gamma^{(n+2)})}{1-\gamma}=\frac{-1}{1-\gamma} qπ0(s1,a4)=−1+γ(−1)+γ2(−1)+⋯=(−1)×1−γ1×(1−γ(n+2))=1−γ−1
~
5、从 ( s 1 , a 5 ) (s_1, a_5) (s1,a5) 开始。不动
episode: s 1 → a 5 s 1 → a 1 s 1 → a 1 ⋯ s_1\xrightarrow{a_5}s_1\textcolor{blue}{\xrightarrow{a_1}s_1\xrightarrow{a_1}\cdots} s1a5s1a1s1a1⋯
q π 0 ( s 1 , a 4 ) = 0 + γ ( − 1 ) + γ 2 ( − 1 ) + ⋯ = ( − 1 ) × 1 × ( 1 − γ ( n + 2 ) ) 1 − γ = − γ 1 − γ q_{\pi_0}(s_1, a_4)=0+\gamma (-1)+\gamma^2(-1)+\cdots=(-1)\times\frac{1\times(1-\gamma^{(n+2)})}{1-\gamma}=\frac{-\gamma}{1-\gamma} qπ0(s1,a4)=0+γ(−1)+γ2(−1)+⋯=(−1)×1−γ1×(1−γ(n+2))=1−γ−γ

策略改进: 让 s 1 s_1 s1 处选择 执行动作 a 2 a_2 a2 或 动作 a 3 a_3 a3
——————————
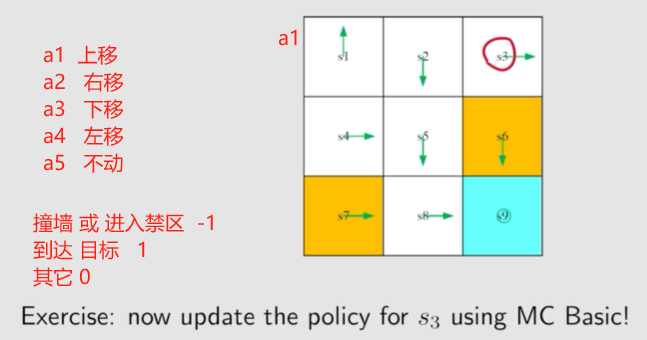
练习:


a 1 a_1 a1: 上移
a 2 a_2 a2: 右移
a 3 a_3 a3: 下移
a 4 a_4 a4: 左移
a 5 a_5 a5: 不动
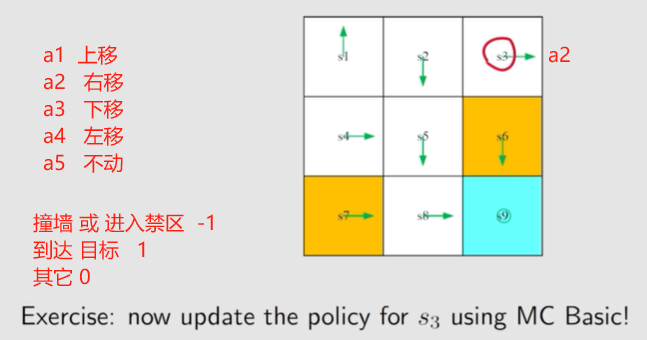
通过 观察 发现, 应该 让 s 3 s_3 s3 往左 🤣
讨论 s 3 s_3 s3 时,所有动作均纳入考量范围。
s 3 s_3 s3 上一个策略的动作的 a 2 a_2 a2 右移
若是再次 进入当前状态,将采取之前策略的动作。
1、从 ( s 3 , a 1 ) (s_3, a_1) (s3,a1) 开始。上移 撞墙
episode: s 3 → a 1 s 3 → a 2 s 3 → a 2 ⋯ s_3\xrightarrow{a_1}s_3\textcolor{blue}{\xrightarrow{a_2}s_3\xrightarrow{a_2}\cdots} s3a1s3a2s3a2⋯
q π 0 ( s 3 , a 1 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + ⋯ = ( − 1 ) × 1 × ( 1 − γ ( n + 2 ) ) 1 − γ = − 1 1 − γ q_{\pi_0}(s_3, a_1)=-1+\gamma (-1)+\gamma^2(-1)+\cdots=(-1)\times\frac{1\times(1-\gamma^{(n+2)})}{1-\gamma}=\frac{-1}{1-\gamma} qπ0(s3,a1)=−1+γ(−1)+γ2(−1)+⋯=(−1)×1−γ1×(1−γ(n+2))=1−γ−1
2、从 ( s 3 , a 2 ) (s_3, a_2) (s3,a2) 开始。 右移 撞墙
episode: s 3 → a 2 s 3 → a 2 s 3 → a 2 ⋯ s_3\xrightarrow{a_2}s_3\textcolor{blue}{\xrightarrow{a_2}s_3\xrightarrow{a_2}\cdots} s3a2s3a2s3a2⋯
q π 0 ( s 3 , a 2 ) = − 1 + γ ( − 1 ) + γ 2 ( − 1 ) + ⋯ = ( − 1 ) × 1 × ( 1 − γ ( n + 2 ) ) 1 − γ = − 1 1 − γ q_{\pi_0}(s_3, a_2)=-1+\gamma (-1)+\gamma^2(-1)+\cdots=(-1)\times\frac{1\times(1-\gamma^{(n+2)})}{1-\gamma}=\frac{-1}{1-\gamma} qπ0(s3,a2)=−1+γ(−1)+γ2(−1)+⋯=(−1)×1−γ1×(1−γ(n+2))=1−γ−1
3、从 ( s 3 , a 3 ) (s_3, a_3) (s3,a3) 开始。 下移 进入禁止区
episode: s 3 → a 3 s 6 → a 3 s 9 → a 5 s 9 → a 5 s 9 → a 5 s 9 ⋯ s_3\xrightarrow{a_3}s_6\xrightarrow{a_3}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\cdots s3a3s6a3s9a5s9a5s9a5s9⋯
q π 0 ( s 3 , a 3 ) = − 1 + γ 1 + γ 2 1 + γ 3 1 + ⋯ = − 1 + 1 1 − γ = γ 1 − γ q_{\pi_0}(s_3, a_3)=-1+\gamma1+\gamma^21+\gamma^31+\cdots=-1+\frac{1}{1-\gamma}=\frac{\gamma}{1-\gamma}~~ qπ0(s3,a3)=−1+γ1+γ21+γ31+⋯=−1+1−γ1=1−γγ ✔
4、从 ( s 3 , a 4 ) (s_3, a_4) (s3,a4) 开始。左移
episode: s 3 → a 4 s 2 → a 3 s 5 → a 3 s 8 → a 2 s 9 → a 5 s 9 → a 5 s 9 → a 5 ⋯ s_3\xrightarrow{a_4}s_2\xrightarrow{a_3}s_5\xrightarrow{a_3}s_8\xrightarrow{a_2}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}s_9\xrightarrow{a_5}\cdots s3a4s2a3s5a3s8a2s9a5s9a5s9a5⋯
q π 0 ( s 3 , a 4 ) = 0 + γ 0 + γ 2 0 + γ 3 1 + γ 4 1 + γ 5 1 + ⋯ = γ 3 1 − γ q_{\pi_0}(s_3, a_4)=0+\gamma0+ \gamma^20+ \gamma^31+ \gamma^41+ \gamma^51+\cdots=\frac{\gamma^3}{1-\gamma} qπ0(s3,a4)=0+γ0+γ20+γ31+γ41+γ51+⋯=1−γγ3
5、从 ( s 3 , a 5 ) (s_3, a_5) (s3,a5) 开始。 不动
episode: s 3 → a 5 s 3 → a 2 s 3 → a 2 s 3 → a 2 ⋯ s_3\xrightarrow{a_5}s_3\textcolor{blue}{\xrightarrow{a_2}s_3\xrightarrow{a_2}s_3\xrightarrow{a_2}\cdots} s3a5s3a2s3a2s3a2⋯
q π 0 ( s 3 , a 5 ) = 0 + γ ( − 1 ) + γ 2 ( − 1 ) + γ 3 ( − 1 ) + ⋯ = − 1 1 − γ q_{\pi_0}(s_3, a_5)=0+\gamma(-1)+\gamma^2(-1)+\gamma^3(-1)+\cdots=\frac{-1}{1-\gamma} qπ0(s3,a5)=0+γ(−1)+γ2(−1)+γ3(−1)+⋯=1−γ−1
向下 a 3 a_3 a3 进入 禁止区最大。!!!只是中间策略,还不是最优策略。
——————————————————————
示例 2:
episode 长度的影响
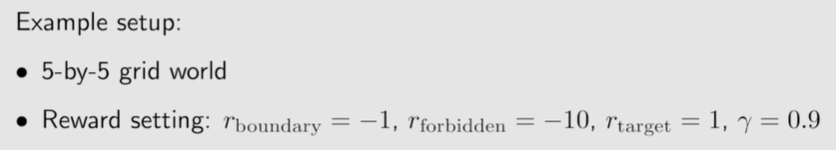

当 episode length 较短时,只有接近目标的状态具有非零状态值。
随着 episode length 的增加,距离目标较近的状态比距离目标较远的状态更早具有非零值。
长到足以找到目标即可。
————————
从一个状态出发,agent 必须至少经过一定的步数才能到达目标状态,然后才能获得正奖励。如果 episode length 小于所需的最小步数,回报为零,估计的状态值也为零。在本例中,episode length 必须不少于15,这是从左下角状态开始到达目标所需的最小步数。
上述分析涉及到一个重要的奖励设计问题——稀疏奖励,稀疏奖励是指除非达到目标,否则无法获得正奖励的情况。稀疏的奖励设置要求玩家的 episode 长度应足以达到目标。当状态空间很大时,这个需求很难满足。因此,稀疏奖励问题降低了学习效率。
在上述网格世界的例子中,我们可以重新设计奖励设置,使智能体在达到接近目标的状态时获得一个小的正奖励。这样可以在目标周围形成一个“吸引场”,使 agent 更容易找到目标。
——————
5.3 MC Exploring Starts
P4
MC Basic 算法的优缺点:
1、优点: 清晰揭示核心思想
2、缺点: 过于简单 不实用
具体原因:

对 MC Basic 算法 进行改进:

高效使用数据:
first-visit:只有第一次遇到的时候估计, 后续遇到不再进行估计。
every-visit:每次遇到都估计

就样本使用效率而言,every-visit 策略是最好的。
如果一个 episode 足够长,以至于它可以多次访问所有 状态-动作对,那么这个 episode 可能足以使用 every-visit 策略 估计所有动作值。然而,every-visit 策略获得的样本是相关的,因为从第二次访问开始的轨迹只是从第一次访问开始的轨迹的子集。然而,如果两次访问在轨迹上彼此距离较远,则相关性不强。
- 额外参数用于 判断两次访问距离的远近?
5.3.2
何时更新策略?
方式一:在策略评估步骤中,收集从状态-动作对开始的所有 episodes,然后使用 平均 return 来近似动作值。
- MC Basic 算法所采用的。
- agent 必须等到所有 episodes 都收集完毕。
方式二:使用 单个 episode 的 return 来近似动作值。✔
- 得到一个 episode 的结果就改进
- 逐步改善 策略
GPI: Generalized policy iteration
- 在 policy-evaluation 和 policy-improvement 进程间不断切换。
搜索 最佳策略 的方法: MC Exploring Starts 【MC Basic 的进阶版本】
1、episode 获取: 状态-动作 对 集合
2、策略 评估 和 改进
- 从 后往前算

选择 MC Exploring Starts 的原因:
Exploring:理论上,只有充分探索了每个状态的每个动作值,我们才能选到最佳动作。如果一个行动没有被探索,这个行动可能恰好是最优的,这样错过了最佳动作。
- 从每一个 ( s , a ) (s, a) (s,a) 出发, 都要有 episode, 这样可以用后面的 reward 来估计 return,进一步估计 action value。
Starts:
要访问每一个 ( s , a ) (s, a) (s,a), 获取后面生成 reward 的数据。两个方式:
1、考虑 从 ( s , a ) (s, a) (s,a) 开始一个 episode,
2、从其它的 ( s , a ) (s, a) (s,a) 开始, 经过 所需的 ( s , a ) (s, a) (s,a) , 后面的数据也可以用于估计这个 ( s , a ) (s, a) (s,a) 的 return 。【visit】
visit 的方式 由于 策略 和 环境 的随机性,无法保证 从 某一个 ( s , a ) (s, a) (s,a) 开始一定经过 剩下的 ( s , a ) (s, a) (s,a)。
——> 对于 任意一个 ( s , a ) (s, a) (s,a) , 保证一定有一个 episode 从该 ( s , a ) (s, a) (s,a) 开始。
在实践中,exploring starts 很难实现。对于许多应用,特别是那些涉及与环境进行物理交互的应用,很难从每个 状态-动作对 开始收集所有 的 episodes。
5.4 MC ε-Greedy:无需 exploring starts
P5 - P6
exploring starts: 要求每个 状态-动作对 都可以被访问足够多次。 ——> 软策略 亦可 达到
软策略: 每一个 action 都有可能 执行。
确定的策略:贪心策略
随机策略: soft policy 中 的 ε \varepsilon ε-greedy
soft policy: 任一状态 采取 任一动作 的 概率均为 正。
当 有限个 状态-动作对 开始的 episodes 已经可以覆盖 所有的 状态-动作对, 此时 可以 无需 exploring starts。
ε 贪心策略
π ( a ∣ s ) = { 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) , 贪心动作 ε ∣ A ( s ) ∣ , 其它动作 \pi(a|s)=\left\{ \begin{aligned} &1- \frac{\varepsilon}{|\mathcal{A}(s)|} (|\mathcal{A}(s)| - 1), &贪心动作\\ &\frac{\varepsilon}{|\mathcal{A}(s)|}, &其它动作\\ \end{aligned} \right. π(a∣s)=⎩ ⎨ ⎧1−∣A(s)∣ε(∣A(s)∣−1),∣A(s)∣ε,贪心动作其它动作
- ε ∈ [ 0 , 1 ] \varepsilon\in[0, 1] ε∈[0,1], ∣ A ( s ) ∣ |\mathcal{A}(s)| ∣A(s)∣ 是 动作集 s s s 的长度。
- 选择 贪心动作的 几率总是 大于 其它动作。 因为 1 − ε ∣ A ( s ) ∣ ( ∣ A ( s ) ∣ − 1 ) = 1 − ε + ε ∣ A ( s ) ∣ ≥ ε ∣ A ( s ) ∣ 1- \frac{\varepsilon}{|\mathcal{A}(s)|} (|\mathcal{A}(s)| - 1) = 1-\varepsilon+\frac{\varepsilon}{|\mathcal{A}(s)|}\geq\frac{\varepsilon}{|\mathcal{A}(s)|} 1−∣A(s)∣ε(∣A(s)∣−1)=1−ε+∣A(s)∣ε≥∣A(s)∣ε

使用 ε ε ε 贪心策略 的原因: 平衡 exploitation 和 exploration
exploitation VS exploration:
exploitation:充分利用。 知道某个 action 的 action value 比较大,下一时刻马上实施 该动作。
- ε ε ε = 0, 贪心, 看当前
exploration:探索。虽然知道 某个 action 当前有更多的 reward, 但认为 当前信息 存在不完备问题, 仍考虑探索 其它 action。
- ε ε ε = 1, 对 每个动作的 选择概率 相同, 均匀分布,探索性 更强。
如何 将 ε ε ε 贪心策略 运用到 基于 MC 的强化学习 算法?
Π \Pi Π:所有 可能策略 的集合
策略改进步骤:
π k + 1 ( s ) = arg max π ∈ Π ∑ a π ( a ∣ s ) q π k ( s , a ) \pi_{k+1}(s)=\arg\max_{\pi\in \textcolor{blue}{\Pi}}\sum_{a}\pi(a|s)q_{\pi_k}(s, a) πk+1(s)=argπ∈Πmaxa∑π(a∣s)qπk(s,a)
最优策略为:
π k + 1 ( a ∣ s ) = { 1 , a = a k ∗ 0 , a ≠ a k ∗ \pi_{k+1}(a|s)=\left\{ \begin{aligned} &1, &a = a_k^*\\ &0, &a \neq a_k^*\\ \end{aligned} \right. πk+1(a∣s)={1,0,a=ak∗a=ak∗
其中 a k ∗ = arg max a q π k ( s , a ) a_k^*=\arg\max\limits_{a}q_{\pi_k}(s, a) ak∗=argamaxqπk(s,a)
————————————————————
Π ε \textcolor{blue}{\Pi_{\varepsilon}} Πε: ε \varepsilon ε 给定 时的 ε \varepsilon ε 贪心策略 集合
策略改进步骤:
π k + 1 ( s ) = arg max π ∈ Π ε ∑ a π ( a ∣ s ) q π k ( s , a ) \pi_{k+1}(s)=\arg\max_{\pi \in \textcolor{blue}{\Pi}_{\varepsilon}}\sum_{a}\pi(a|s)q_{\pi_k}(s, a) πk+1(s)=argπ∈Πεmaxa∑π(a∣s)qπk(s,a)
最优策略为:
π k + 1 ( a ∣ s ) = { 1 − ∣ A ( s ) ∣ − 1 ∣ A ( s ) ∣ ε , a = a k ∗ 1 ∣ A ( x ) ∣ ε , a ≠ a k ∗ \pi_{k+1}(a|s)=\left\{ \begin{aligned} & \textcolor{blue}{1-\frac{|\mathcal{A}(s)|-1}{|\mathcal{A}(s)|}\varepsilon}, &a = a_k^*\\ &\textcolor{blue}{\frac{1}{|\mathcal{A}(x)|}\varepsilon}, &a \neq a_k^*\\ \end{aligned} \right. πk+1(a∣s)=⎩ ⎨ ⎧1−∣A(s)∣∣A(s)∣−1ε,∣A(x)∣1ε,a=ak∗a=ak∗
$\Pi$ Π \Pi Π

————————
P6
ε \varepsilon ε-greedy 的探索性
当 ε \varepsilon ε 比较大时, 探索性较强, 可以 不用 exploring starts 这样的条件。从某一些 (s, a) 对 出发的 episodes 就能 覆盖 其它 所有 的 (s, a) 对。 状态-动作 对

ε = 1 \varepsilon=1 ε=1, 均匀分布, 每个 action 的执行概率相等。
25 个状态, 每个状态 有 5 个 action。一共 25 * 5 = 125 个 状态-动作 ( s , a ) (s, a) (s,a) 对。
从访问次数可以看出, 从 某一些 ( s , a ) (s, a) (s,a) 出发, 即可覆盖其它所有的 ( s , a ) (s, a) (s,a)。

当 ε \varepsilon ε 比较小时, 当 步数 达到 1 万时, 仍有 状态-动作对 未被探索到。
例子:
按照以下步骤运行 MC - greedy 算法:
在每次迭代中:在 episode 生成步骤中,使用之前的策略生成一个100万步 的 episode !
在其余步骤中,使用单个 episode 更新策略。
两次迭代可以得到最优的 ε \varepsilon ε-greedy 策略。
5.5 ε − ~~\varepsilon- ε− greedy 策略的探索与利用
ε \varepsilon ε-greedy 策略:
探索性较强,不需要 exploring starts 条件。
获得的策略通常不是最优的。——> 设置较小的 ε \varepsilon ε
- 因为 最终获得的策略 只是 ε \varepsilon ε-greedy 策略 集合 Π ε \Pi_{\varepsilon} Πε中的最优。
ε \varepsilon ε 逐渐减小:一开始设置较大的 ,较强的探索能力;后面 让 ε \varepsilon ε 逐渐趋向于 0, 增加获得最优策略的可能性。
例子:

随着 ε \varepsilon ε 增大, 所获得的最优策略变差。
如果策略中具有最大概率的行为是相同的,则两个 ε \varepsilon ε 贪婪策略是一致的 (consistent)。
因此一般在后面 让 ε \varepsilon ε 逐渐趋向于 0。
exploration探索 和 exploitation利用 构成了强化学习的基本权衡。
探索意味着策略可以采取尽可能多的行动。这样,所有的动作都可以被访问和评估。
利用是指改进后的策略应采取 动作值最大的贪心行为。但是,由于探索不够,目前得到的动作值可能不准确,所以我们在利用的同时要不断探索,避免遗漏最优动作。
ε − \varepsilon- ε− greedy 策略 提供了一种平衡探索和利用的方法。
一方面, ε − \varepsilon- ε− greedy 策略 采取贪心行为的概率更高,从而可以利用估计值。
另一方面, ε − \varepsilon- ε− greedy 策略 也有机会采取其他行动,使其能够继续探索。
ε − \varepsilon- ε− greedy 策略 不仅用于基于 MC 的强化学习算法,还用于其他强化学习算法,如第 7 章介绍的时间差分学习。
ε \varepsilon ε 减小 ——> 利用
ε \varepsilon ε 增大 ——> 探索
√ 5.6 小结:
MC Basic:这是最简单的基于 MC 的强化学习算法。该算法通过将 策略迭代 算法中基于模型的策略评估步骤替换为基于无模型 MC 的估计组件而获得。给定足够的样本,保证算法收敛到最优策略和最优状态值。
MC Exploring Starts:该算法是 MC Basic 的一个变体。MC Basic 算法可以采用 first-visit 策略 或 every-visit 策略来更有效地利用样本。
MC ε \varepsilon ε-Greedy:这个算法是 MC Exploring Starts 的一个变体。具体来说,在策略改进步骤中,它搜索 最优的 ε \varepsilon ε-greedy 策略,而不是贪心策略。这样可以增强策略的探索能力,从而消除 exploring starts 的条件。
exploration探索 和 exploitation利用 之间的权衡。随着 ε \varepsilon ε 值的增大, ε \varepsilon ε-greedy 策略的探索能力增强,贪心行为的利用减少。另一方面,如果 ε \varepsilon ε 的值降低,我们可以更好地利用贪心行为,但探索能力下降。
————————————————
√ 5.7 Q&A
均值估计问题:基于随机样本计算随机变量的期望值。
免模型的 基于 MC 的强化学习 的核心思想:
将 策略迭代算法 中基于模型的策略评估步骤 ——> 免模型 的 基于 MC 的策略评估步骤。
initial-visit, first-visit, every-visit
它们是在一个 回合episode 中使用样本的不同策略。
一个 episode 可能会访问在许多 状态-动作 组合中。
initial-visit策略使用 整个 episode 来估计 初始 状态-动作对的 动作值。 【MC Basic】
every-visit 和 first-visit 策略可以更好地利用给定的样本。
如果在每次访问状态-动作对时, 都用 episode 的其余部分估计其动作值,则这种策略称为every-visit。【MC ε \varepsilon ε-Greedy】
如果我们仅在 状态-动作对 第一次被访问时估计其动作值,这样的策略被称为first-visit。
- first-visit 和 every-visit 哪个好些呢?一般怎么选择用哪种? P97
——> 样本使用效率上,every-visit 最好,但若是两次访问较近,可能存在相关性。
⭐ 可参考链接: https://deepgram.com/ai-glossary/monte-carlo-learning
——————
习题笔记:
均值估计: 利用一些随机样本来估算一个随机变量的 均值 或 期望。
研究 均值估计问题的原因:状态值 和 动作值 为随机变量期望
蒙特卡罗(Monte Carlo)估计在强化学习中的作用是什么?
- MC 是用来直接估计动作值的。注意本次课中没有用 MC 估计状态值,因为即使估计出来状态值,还需要进一步估计动作值,因此要一步到位估计动作值。
在强化学习中“模型”(model):表示 状态转换 和 奖励函数 的概率分布
在强化学习中“数据”:从与环境的互动中获得的经验样本
MC Basic算法 把 策略迭代算法 中 依赖模型的部分 用不依赖模型的部分替换掉得到的算法。
MC Basic 算法的每次迭代有 2 个步骤:策略评估 和 策略改进

相关文章:

▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch5 蒙特卡洛方法【model-based ——> model-free】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 学堂在线 习题 2、 过 电子书 是否遗漏 【下载:本章 PDF GitHub 页面链接 】 【第二轮 才整理的,忘光了。。。又看了一遍视频】 3、 过 MOOC 习题 看 PDF 迷迷糊糊, 恍恍惚惚。…...
【linux】Valgrind工具集详解(十六):交叉编译、移植到arm(失败)
1、源码下载 官网:https://valgrind.org/ 源码:https://valgrind.org/downloads/current.html 2、配置 ./configure CC=arm-linux-gnueabihf-gcc \CXX=arm-linux-gnueabihf-g++ \AR=arm-linux-gnueabihf-ar \--host=arm-linux-gnueabihf \--pr...
答案版)
前端面试题(七)答案版
面试形式:线下面试:时长20分钟 特殊要求:996加班30k上限 面试评价:技术题 面试官:前端技术人员 面试官的提问大纲:本公司招聘要求本人简历 面试流程以及面试题: 第一个环节:自…...
为微信小程序项目添加eslint
背景 在使用vscode开发微信小程序的过程中,修改js的时候发现没有报错提示,让我很不习惯,所以想为微信小程序项目添加eslint配置 编码实战 为微信小程序配置ESLint可以遵循以下步骤: 安装ESLint及其相关插件 首先,…...

Win10用户必看:最好用最稳定的版本在此,值得一试!
在Win10电脑操作中,用户可以根据的需要,下载安装不同的系统版本。现在,许多用户好奇Win10哪个版本最好用最稳定?接下来小编给大家推荐最好用最稳定的Win10版本,这些系统版本经过优化升级,相信会给大家带来最…...

处理文本内容的命令和正则表达式
处理文本内容的命令 正则表达式匹配的是文本内容,linux的文本三剑客 都是针对文本内容 文本三剑客: grep 过滤文本内容 sed 针对文本内容进行增删改查 awk 按行取列 文本三剑客都是按行进行匹配。 grep grep的作用就是使用正则表达式来匹配文本内…...

AI与音乐:当技术与艺术发生冲突
AI在创造还是毁掉音乐? 在科技日新月异的今天,人工智能(AI)已经渗透到了我们生活的方方面面,音乐领域也不例外。然而,尽管AI为音乐创作带来了前所未有的便利,我却深感其正在毁掉音乐的本质。 …...
java泛型学习
没有java泛型会存在的问题 假设我们有一个方法,希望通过传递不同类型的参数,输出不同类型的对象值。正常情况下我们可能会写不同的方法来实现,但是这样会导致类不断增加,并且类方法很相似,不能够复用。进而导致类爆炸…...

vscode c++ 开发环境配置
今天各位同学已经安装了mingw环境,但部分同学vscode开发环境又问题,究其原因,还是vscode 编译环境配置错误,有问题的同学 按如下步骤处理: 1、卸载相关插件。按下列步骤重新安装插件。 2、继续在搜索框中搜索并安装 C…...
PHP安装配置
文章目录 1.下载PHP2.配置环境变量3.Apache安装配置 1.下载PHP PHP即“超文本预处理器”,是一种通用开源脚本语言。PHP是在服务器端执行的脚本语言,与C语言类似,是常用的网站编程语言。PHP独特的语法混合了C、Java、Perl以及 PHP 自创的语法…...

std::vector<>的{}用法与stl中的共享指针
讨论 std::vector<>的{}用法比较方便,在stl中的共享指针中是否适用? 代码 #include <iostream> #include <memory> #include <vector> using namespace std;int main() {vector<int> vt1({1,3,5});vec…...

《FFmpeg开发实战:从零基础到短视频上线》资源下载和内容勘误
资源下载 下面是《FFmpeg开发实战:从零基础到短视频上线》一书用到的工具和代码资源: 1、本书使用的FFmpeg版本为FFmpeg 5.1.2,也可在FFmpeg的github主页上下载最新的FFmpeg源码。 2、本书第12章使用的Android Studio版本为Android Studio D…...
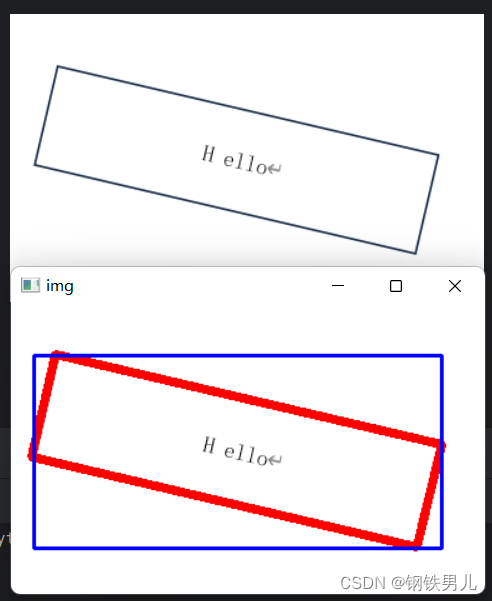
OpenCV目标识别
一 图像轮廓 具有相同颜色或强度的连续点的曲线。 图像轮廓的作用 可以用于图像分析 物体的识别与检测 注意 为了检测的准确性,需要先对图像进行二值化或Canny操作。 画轮廓时会修改输入的图像。 轮廓查找的API findContours(img,mode,ApproximationMode,...)…...
密码学及其应用——为什么选择接近的质数因子对RSA加密算法不安全?
RSA加密算法是一种广泛使用的非对称加密算法,它的安全性依赖于大整数分解的难度。具体来说,RSA算法生成的公钥包含一个大整数N,这是两个大质数p和q的乘积。然而,如果这两个质数p和q太接近,则可以相对容易地对N进行因式…...

爱心商城管理系统的设计
管理员账户功能包括:系统首页,个人中心,管理员管理,企业管理,用户管理,论坛管理,商品管理,公告管理,用户捐赠 企业账户功能包括:系统首页,个人中…...

【python】linux下安装chromedriver
首先,安装selenium模块 pip3 install selenium查看系统内chrome版本: google-chrome --version 根据谷歌浏览器版本下载对应的浏览器驱动版本: wget https://storage.googleapis.com/chrome-for-testing-public/126.0.6478.114/linux64/ch…...

Day18—使用Scrapy框架快速开发爬虫
Scrapy是一个强大的Python框架,用于快速开发爬虫程序。它提供了一整套工具来处理网页爬取和数据提取,非常适合于数据挖掘和信息抓取。本文将详细介绍如何使用Scrapy框架,包括创建项目、编写爬虫规则、设置中间件和管道等。 1. Scrapy框架概述 Scrapy框架以其高性能、易用性…...
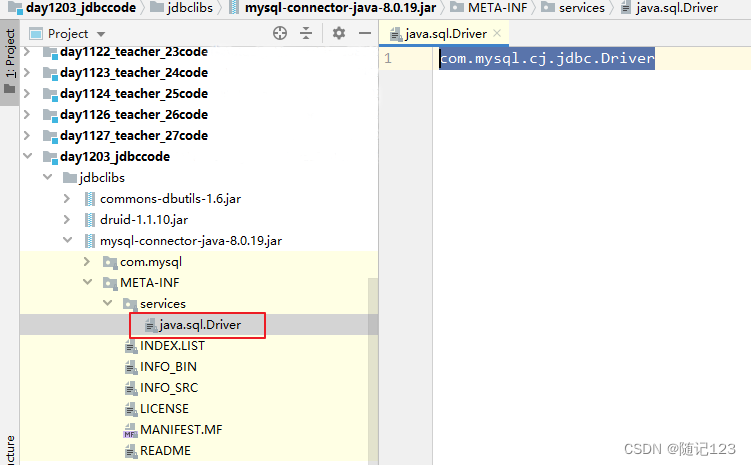
04--MySQL8.0_JDBC
第一章 JDBC概述 之前我们学习了JavaSE,编写了Java程序,数据保存在变量、数组、集合等中,无法持久化,后来学习了IO流可以将数据写入文件,但不方便管理数据以及维护数据的关系; 后来我们学习了数据库管理软件MySQL,可以方便的管理数据1。 那么如何将它俩结合起来呢?即…...
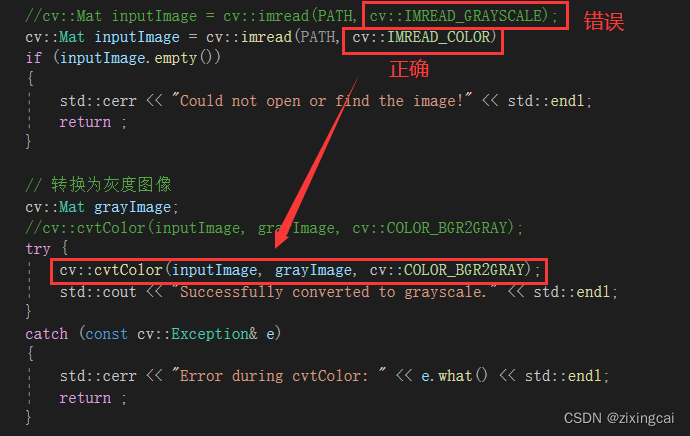
OPENCV中0x00007FFE5F35F39C发生异常
原因:读取图片时已经为灰度图像,又进行了一次灰度处理cvtColor 解决方法:如上图所示,将cv::imread的第二个参数改为cv::IMREAD_COLOR;或者保留cv::IMREAD_GRAYSCALE,删去后面的cv::cvtColor...
 -- 第三部分(行为型模式))
Python 设计模式(第2版) -- 第三部分(行为型模式)
Python 设计模式(第2版) 再介绍下行为型设计模式。 行为型模式,顾名思义,它主要关注的是对象的责任。它们用来处理对象之间的交互,以实现更大的功能。行为型模式建议:对象之间应该能够彼此交互,同时还应该是松散耦合…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...