【算法时间复杂度】学习记录
最近开算法课,开几篇文章记录一下算法的学习过程。
关于算法的重要性
学习计算机当程序员的话,在编程过程中是绕不开算法这个大矿山的,需要我们慢慢挖掘宝藏。
算法(Algorithm)是指用来操作数据、解决程序问题的一组方法。对于同一个问题,使用不同的算法,也许最终得到的结果是一样的,但在过程中消耗的资源和时间却会有很大的区别。
时间复杂度
先了解一下关于时间复杂度的相关概念:
涉及到代码所用时间,我们可以琢磨把代码跑一遍记录一下起始和结束的时间得出整个算法用时,但是很多情况我们是需要理论分析的,不是上机测试,另外硬件的不同也会导致时间有差异。这时候就出现了一个叫做大O表示法。
算法的时间复杂度,用来度量算法的运行时间,记作: T(n) = O(f(n))。它表示随着 输入大小n 的增大,算法执行需要的时间的增长速度可以用 f(n) 来描述。
时间复杂度分析的基本策略是:从内向外分析,从最深层开始分析。如果遇到函数调用,要深入函数进行分析
常见描述时间复杂度的表达式:
O(1):常量时间
O(n):线性时间
O(log n):对数时间
O(n^2):二次方时间
O(2^n):指数时间
O(n!):阶乘时间
常见的算法时间复杂度分析:
O(1)< O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n) <O(n!) < O(n^n)
如何计算时间复杂度
O(1)
int func(int n)
{n++;return n*2;
}
上面代码运行时间是一个常量,虽然运行时间是2,但是用O(1)表示,代表时间复杂度是一个常数。
O(n)
int func(int n)
{int sum = 0;for(int i=0; i<n; i++){sum = sum + i;}return sum;
}
上面程序我们分析函数的执行时间是随着n的变化成线性关系:n+2,用O(n)表示线性。
O(n^2 )
int func(int n)
{int sum = 0;for(int i=0; i<n; i++){for(int j=0; j<n; j++){sum = sum + i + j;}}return sum;
}
上面的程序是两层循环的程序,函数的执行时间是n的2次方关系:n^2+2 ,用O(n^2 )来表示时间复杂度。(关于为什么可以省去低幂的我们下面会说明)
O(2^n)
O(2^n)表示指数复杂度,随着n的增加,算法的执行时间成倍增加,它是一种爆炸式增长的情况。
int func(int n)
{if(n==0) return 1;return func(n) + func(n-1)
}
O(log n)
O(log n)表示对数时间复杂度,算法执行时间和n是一种对数关系。这种类型的算法会在执行的过程中,随着程序的执行其完成某个功能的操作步骤越来越少。 其中,我们所熟知的二分查找法就是一个很好的例子。比如,下面这个代码在一个有序列表中查找某个值的位置,我们通过二分法进行查找。
int func(int a[], int size, int num)
{int left = 0;int right = size-1;while(left <= right){int mid = (left + right)/2;if(a[mid] > num){right = mid - 1;}else if (a[mid] < num){left = mid + 1;}else{return num;}}return -1;
}
O(n!)
这个我不是很了解,找一个网上的例子来说说吧。
旅行商问题
假设有一个旅行商人要拜访n+1个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求得的路径长度为所有路径之中的最小值。
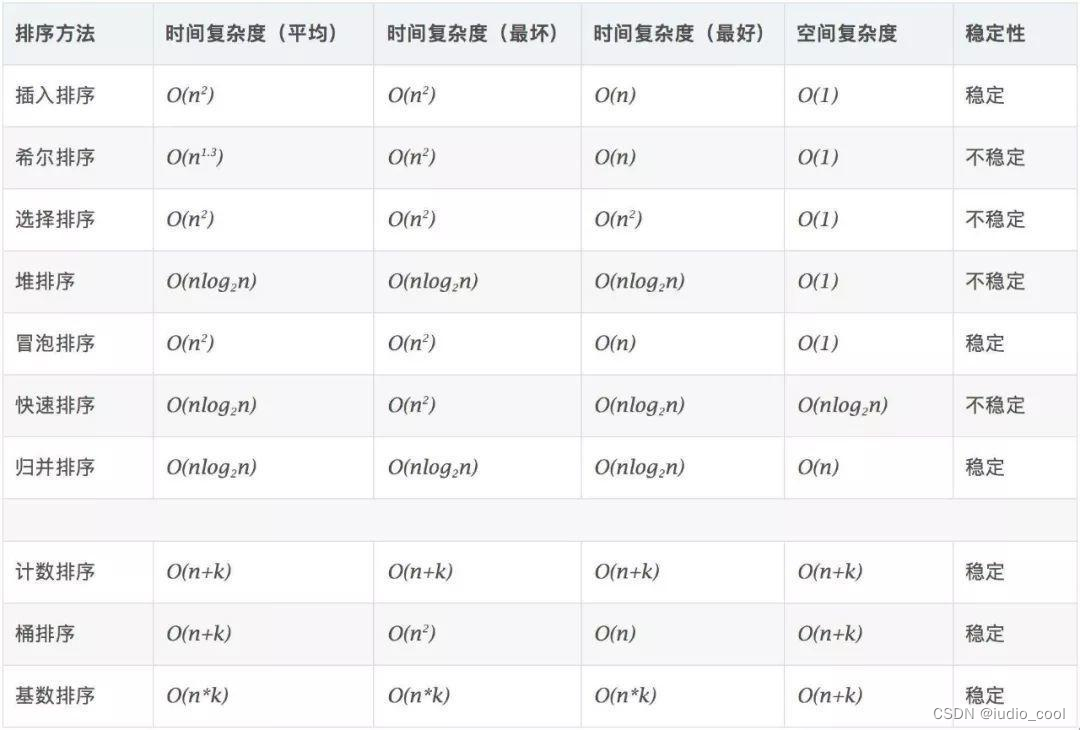
常见算法的时间复杂度
相关文章:

【算法时间复杂度】学习记录
最近开算法课,开几篇文章记录一下算法的学习过程。 关于算法的重要性 学习计算机当程序员的话,在编程过程中是绕不开算法这个大矿山的,需要我们慢慢挖掘宝藏。 算法(Algorithm)是指用来操作数据、解决程序问题的一组…...

汽车车机芯片Linux系统内核编译问题总结
谈到车机,很多人会想到华为问界上装的大屏车机,号称车机的天花板,基于鸿蒙OS的,而今天谈到的车机芯片用的是linux内核Kernel,对于它的编译,很多人一时会觉得头大,的确如果工具不是很齐全,就会遇到这样那样的问题,但是过程都会有错误提示,按照错误提示基本可以解决,而…...

Android13 音量曲线调整
Android13 音量曲线调整 Android13 上配置文件的路径: /vendor/sprd/modules/audio/engineconfigurable_apm/工程目录/system/etc/audio_engine_config/audio_policy_engine_stream_volumes.xml /vendor/sprd/modules/audio/engineconfigurable_apm/工程目录/sys…...
OpenHarmony通过MQTT连接 “改版后的华为IoT平台”
一、前言 本篇文章我们使用的是BearPi-HM_Nano开发板:小熊派的主板+E53_IA1扩展板 源码用的是D6_iot_cloud_oc,点击下载BearPi-HM_Nano全量源码 那么为什么要写这篇呢? 前段时间看到OpenHarmony群里,经常有小伙伴问接入华为IoT平台的问题,他们无法正常连接到华为IoT平台等…...
SQS (Simple Queue Service)简介
mazon Simple Queue Service (SQS)是一种完全托管的消息队列服务,可以让你分离和扩展微服务、分布式系统和无服务应用程序。 在讲解SQS之前,首先让我们了解一下什么是消息队列。 消息队列 还是举一个电商的例子,一个用户在电商网站下单后付…...
)
高速PCB设计指南系列(三)
第一篇 高密度(HD)电路的设计 本文介绍,许多人把芯片规模的BGA封装看作是由便携式电子产品所需的空间限制的一个可行的解决方案,它同时满足这些产品更高功能与性能的要求。为便携式产品的高密度电路设计应该为装配工艺…...
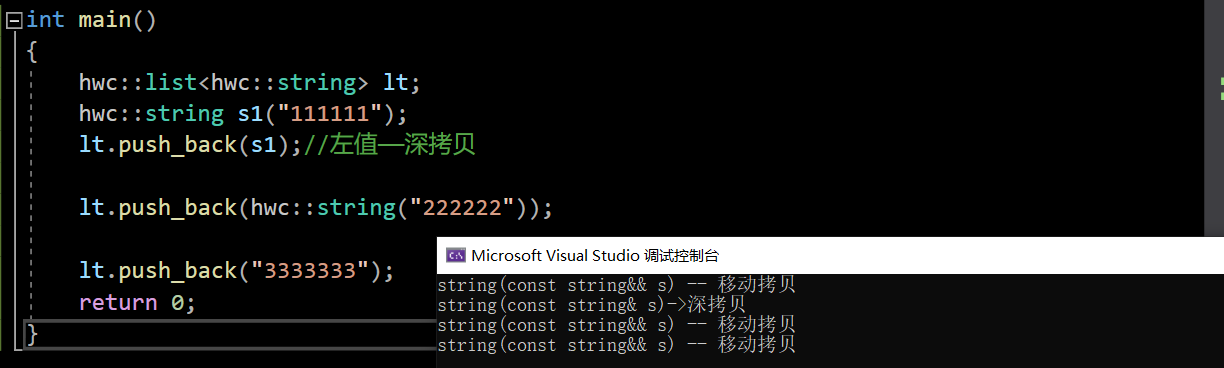
【C++】C++11——左右值|右值引用|移动语义|完美转发
文章目录一、左值与右值1.概念2.引用3.注意二、右值引用的意义1.左值引用意义2.右值引用和移动语义3.容器新增三、万能引用四、完美转发一、左值与右值 1.概念 左值是什么?右值是什么? 左值是一个表示数据的表达式(如变量名或解引用的指针&…...

[ROC-RK3399-PC Pro] 手把手教你移植主线Buildroot(基于2023.02-rc3版本)
🍇 博主主页:Systemcall小酒屋🍇 博主简介:Neutionwei,C站嵌入式领域新星创作者之一,一枚热爱开源技术、喜欢分享技术心得的极客,注重简约风格,热衷于用简单的案例讲述复杂的技术&am…...

重温线性代数
前言 对于普通的数学工作者而言,掌握矩阵、线性空间的基本性质和用法比领会抽象的概念更实用。数学专业的同学需要全面深入学习近世代数的理论和演绎法则,例如模的概念和运算。 总之,我个人认为,不论是微积分、还是线性代数&…...

2023河北沃克HEGERLS甘肃金昌重型仓储项目案例|托盘式四向穿梭车智能密集存储系统在工业行业的创新应用
项目名称:自动化仓储托盘式四向穿梭车智能密集立体库项目 项目合作客户:甘肃省金昌市某集团企业 项目施工地域:甘肃省金昌市 设计与承建单位:河北沃克金属制品有限公司(自主品牌:海格里斯HEGERLS&#x…...

软件测试的案例分析 - 闰年5
文章目的 显示不同的博客能获得多少博客质量分 (这是关于博客质量分的测试 https://www.csdn.net/qc) 这个博客得了 83 分。怎么才能得到更多分数? 正文 我们谈了不少测试的名词, 软件是人写的, 测试计划和测试用例也是人写的, 人总会犯错误。错误发生…...

Linux文件基础I/O
文件IO文件的常识基础IO为什么要学习操作系统的文件操作C语言对于函数接口的使用接口函数介绍如何理解文件文件描述符重定向更新给模拟实现的shell增加重定向功能为什么linux下一切皆文件?文件的常识 1.空文件也要在磁盘占据空间 2.文件 内容 属性 3.文件操作 对…...
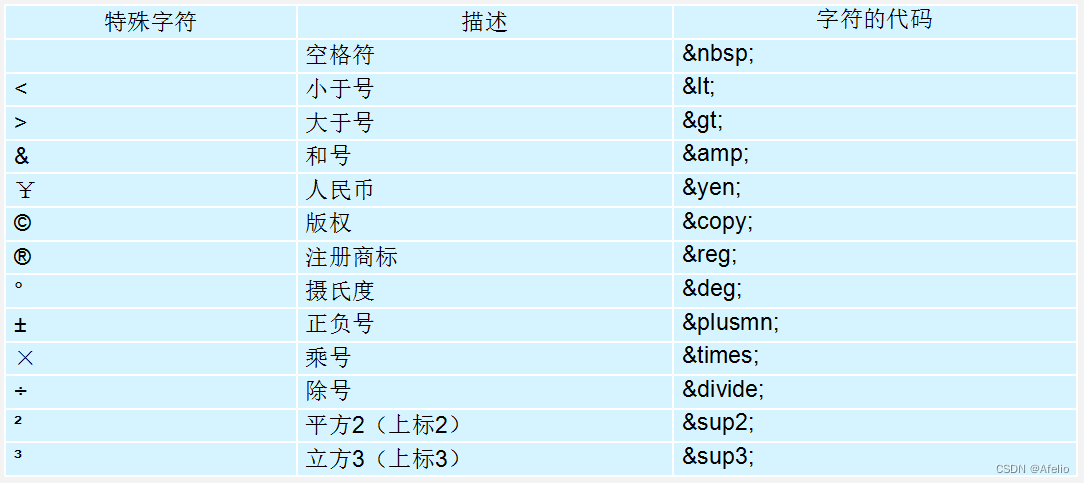
HTML看这一篇就够啦,HTML基础大全,可用于快速回顾知识,面试首选
HTML 1 基础 1.1 DOCTYPE <!DOCTYPE> 文档类型声明,作用就是告诉浏览器使用哪种HTML版本来显示网页。 <!DOCTYPE html> 这句代码的意思是: 当前页面采取的是 HTML5 版本来显示网页. 注意: 声明位于文档中的最前面的位置,处于 标签之前。 …...
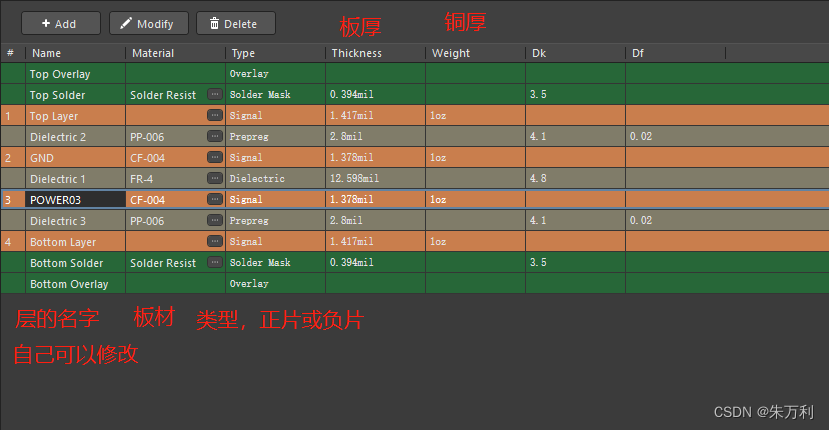
Altium Designer(AD)软件使用记录05-PCB叠层设计
目录Altium Designer(AD)软件使用记录05-PCB叠层设计一、正片层和负片层的介绍1、正片层(Signal)2、负片层(Plane)3、内电层的分割实现二、正片层和负片层的内缩设计1、负片设置内缩20H原则2、正片铺铜设置内缩1、设置规则2、重新铺铜三、AD的层叠设计四、叠层设计需要注意的问…...
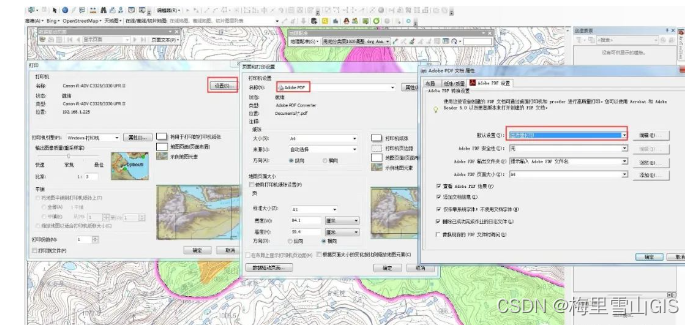
ArcGIS动态表格批量出图
一.产品介绍:ArcGIS动态表格扩展模块Mapping and Charting Solutions,可用于插入动态表格,与数据驱动结合,出图效率无敌。注:优先选择arcgis10.2.2。 二、下载连接: https://www.xsoftnet.com/share/a001CX…...

ChatGPT真神奇,但是也真焦虑
ChatGPT火爆ChatGPT的火爆程度不用说也知道。就目前来说,已经开始冲击各行业了,比如客服、智能助手、语言学习、自然语言处理等等等。。ChatGPT冲击冲击最高的可能就是中间这个段位的了。高段位无法取代,但是低段位,通过使用ChatG…...
mos管驱动与米勒平台介绍、消除
mos驱动设计 1.选择适当的驱动芯片 为了控制MOSFET,需要使用专门的驱动芯片。选择合适的芯片需要考虑MOSFET的电压和电流需求。常见的驱动芯片包括IR2110、IR2184、MIC4424等。 2.设计电路 在驱动电路中,需要加入一些电路元件来保证MOSFET的顺畅工作…...

20230311英语学习
Philosophy of Food: Guidelines for an Authentic Approach to Eating 饮食哲学:值得思考的问题 Whats Philosophical About Food? Philosophy of food finds its basis on the idea that food is a mirror.Eating mirrors the making of a self, that is, the …...
)
【面试题】Nginx面试题汇总(无解答)
什么是Nginx?谈谈个人都理解,项目中是否用到,为什么要用,有什么优点?为什么要用Nginx?为什么Nginx性能这么高?Nginx怎么处理请求的?什么是正向代理和反向代理?使用“反向…...
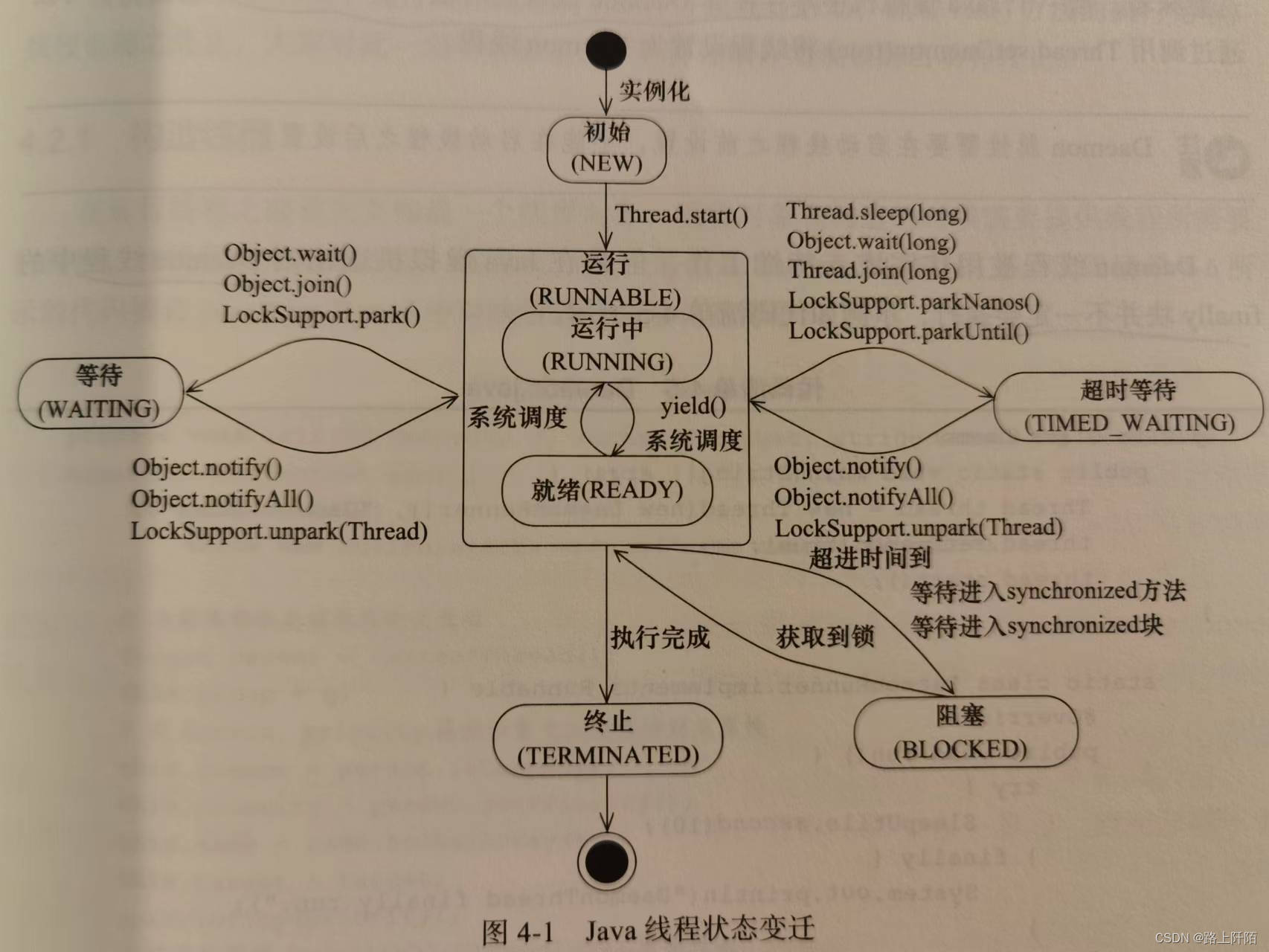
Java面试总结(六)
进程和线程的区别 根本区别: 进程时操作系统资源分配的基本单位,而线程是处理器任务调度和执行的基本单位。 资源开销: 每个进程都有自己独立的代码和数据空间(程序上下文),进程之间的切换开销比较大&…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

OkHttp 中实现断点续传 demo
在 OkHttp 中实现断点续传主要通过以下步骤完成,核心是利用 HTTP 协议的 Range 请求头指定下载范围: 实现原理 Range 请求头:向服务器请求文件的特定字节范围(如 Range: bytes1024-) 本地文件记录:保存已…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

sqlserver 根据指定字符 解析拼接字符串
DECLARE LotNo NVARCHAR(50)A,B,C DECLARE xml XML ( SELECT <x> REPLACE(LotNo, ,, </x><x>) </x> ) DECLARE ErrorCode NVARCHAR(50) -- 提取 XML 中的值 SELECT value x.value(., VARCHAR(MAX))…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...
