(考研湖科大教书匠计算机网络)第四章网络层-第三节1:IPv4地址概述
- 获取pdf:密码7281
- 专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航
文章目录
- 一:IPv4地址概述
- 二:IPv4地址表示方法
- (1)概述
- (2)8位无符号二进制数转十进制正整数
- (3)十进制正整数转8位无符号二进制数
本节对应视频如下
- 【计算机网络微课堂(有字幕无背景音乐版)】:IPv4地址概述
一:IPv4地址概述
IPv4地址:就是给以太网上的每一台主机(或路由器)的每一个接口分配一个在全世界范围内唯一的32比特的标识符。IP地址由因特网名字和数字分配机构(ICANN)进行分配
- 我国用户可向 亚太网络信息中心(APNIC) 申请IP地址,需要缴费。
- 2011年2月3日,互联网号码分配管理局IANA (由ICANN行使职能)宣布,IPv4地址已经分配完毕
- 我国在2014至2015年也逐步停止了向新用户和应用分配IPv4地址。同时全面开展商用部署IPv6
IPv4地址的编址方法经历了如下三个历史阶段
- 分类编址(1981)
- 划分子网(1985)
- 无分类编址(1993)
二:IPv4地址表示方法
(1)概述
IPv4地址表示方法:由于32比特的IPv4地址不方便阅读、记录以及输入等,因此IPv4地址采用点分十进制表示方法以方便用户使用
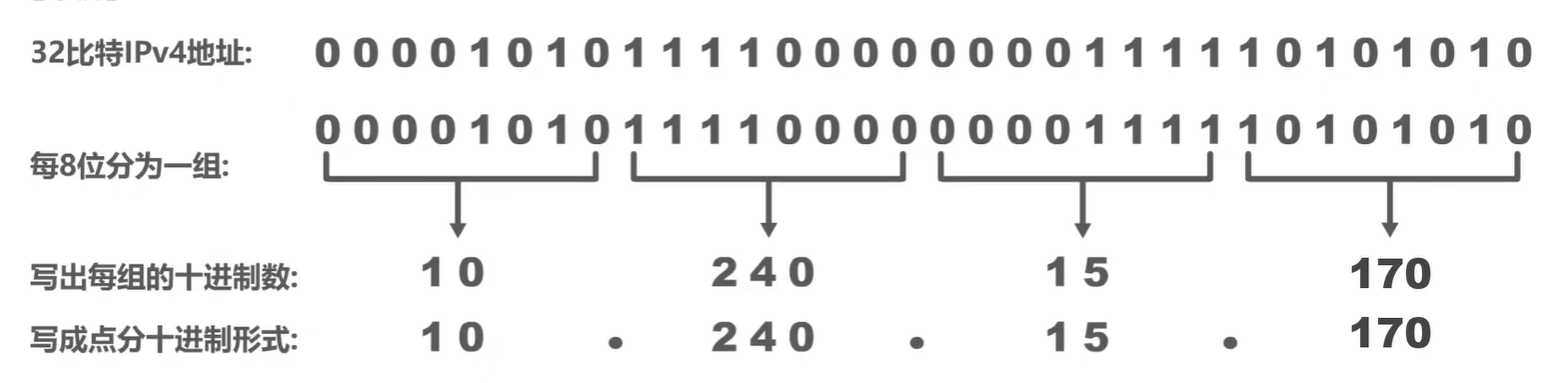
(2)8位无符号二进制数转十进制正整数
- 更多有关进制转换问题可见:(计算机组成原理)第二章数据的表示和运算-第一节1:进位计数及进制转换
二进制数的每个位权值为
| 2102^{10}210 | 292^{9}29 | 282^{8}28 | 272^{7}27 | 262^{6}26 | 252^{5}25 | 242^{4}24 | 232^{3}23 | 222^{2}22 | 212^{1}21 | 202^{0}20 | 2−12^{-1}2−1 | 2−22^{-2}2−2 | 2−32^{-3}2−3 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1024 | 512 | 256 | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 | 0.5 | 0.25 | 0.125 |
8位无符号二进制整数转为十进制整数方法如下:
(b7b6b5b4b3b2b1b0)2=(b7×27+b6×26+b5×25+b4×24+b3×23+b2×22+b1×21+b0×20)10(b_{7}b_{6}b_{5}b_{4}b_{3}b_{2}b_{1}b_{0})_{2}=(b_{7}×2^{7}+b_{6}×2^{6}+b_{5}×2^{5}+b_{4}×2^{4}+b_{3}×2^{3}+b_{2}×2^{2}+b_{1}×2^{1}+b_{0}×2^{0})_{10} (b7b6b5b4b3b2b1b0)2=(b7×27+b6×26+b5×25+b4×24+b3×23+b2×22+b1×21+b0×20)10
举例:
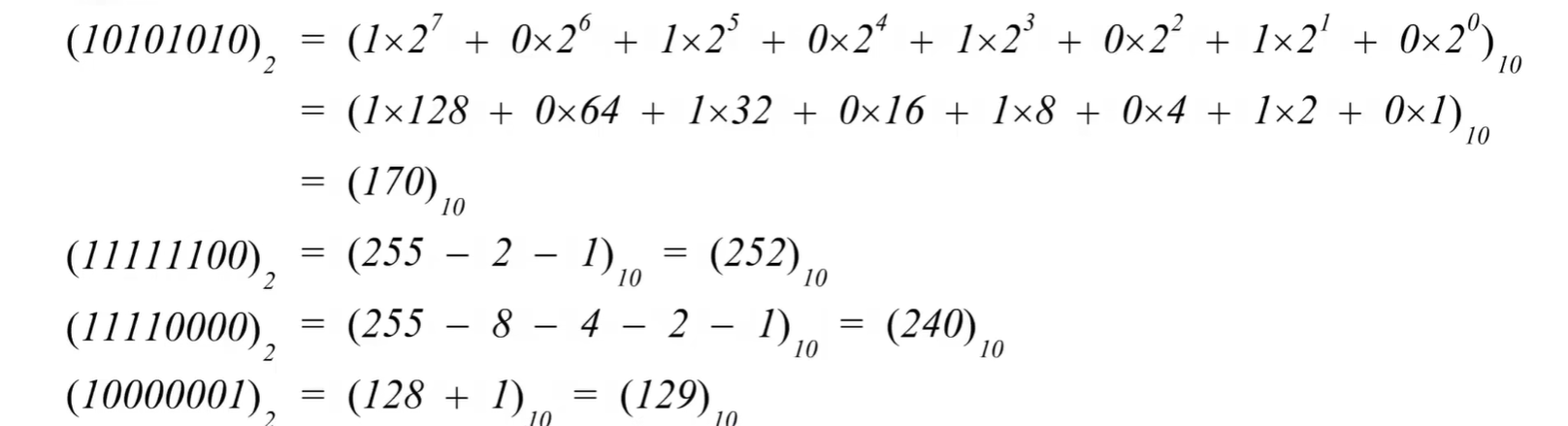
(3)十进制正整数转8位无符号二进制数
基本方法:除2取余法

快速方法:凑值法
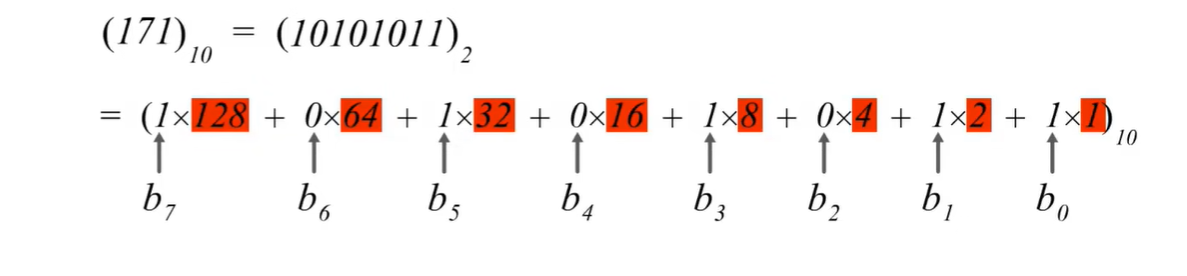
相关文章:
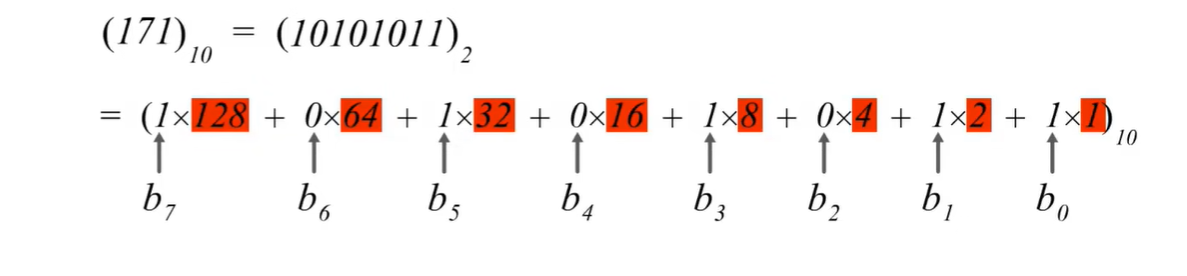
(考研湖科大教书匠计算机网络)第四章网络层-第三节1:IPv4地址概述
获取pdf:密码7281专栏目录首页:【专栏必读】考研湖科大教书匠计算机网络笔记导航 文章目录一:IPv4地址概述二:IPv4地址表示方法(1)概述(2)8位无符号二进制数转十进制正整数ÿ…...

B站Python与OpenCV人脸识别项目超详细记录(对图片、视频、摄像头人脸的检测)
课程来源:一天搞定人脸识别项目!学不会up直接下跪!(pythonopencv)_哔哩哔哩_bilibili 图片来源:感谢王鹤棣先生友情出镜~ 环境配置详见: 在conda虚拟环境中安装OpenCv并在pycharm中使用_cond…...

【Node.js实战】一文带你开发博客项目之Koa2重构(实现session、开发路由、联调、日志)
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,也会涉及到服务端 📃个人状态: 在校大学生一枚,已拿多个前端 offer(秋招) 🚀未…...
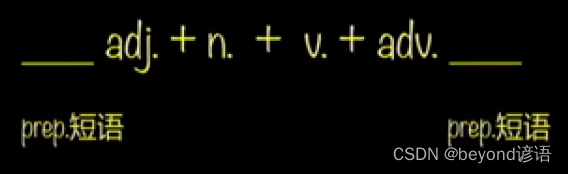
第一部分:简单句——第二章:简单句的补充
简单句的核心构成:一主一谓 主语/宾语/表语 可以变成名词/代词/doing/to do 谓语动词有四种核心变化:三态 一否 时态语态情态否定 简单句的核心:将简单句给写对 简单句的补充:将简单句给写的更好、更充分 简单句的补充 1、限定…...

Spring Security简介
前面我们已经完成了传智健康后台管理系统的部分功能,例如检查项管理、检查组管理、套餐管理、预 约设置等。接下来我们需要思考2个问题: 问题1:在生产环境下我们如果不登录后台系统就可以完成这些功能操作吗? 答案显然是否定的&am…...
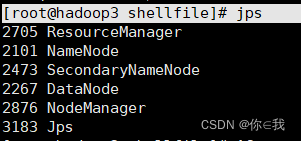
Hadoop安装 --- 简易安装Hadoop
目录 1、使用xftp工具 在opt目录下创建install和soft文件 2、使用xftp工具 将压缩包上传到install文件 3、编写shell脚本 3.1、创建目录来放shell脚本 3.2、创建autoinsatll.sh文件并修改权限 3.3、编写autoinsatll.sh 文件 刷新资源 运行文件 格式化 启动所有进程 Ha…...

俞军产品方法论,消化吸收,要点整理
一、总体概括二、产品经理、价值、用户模型、交易模型三、价值、产品和企业的价值生存游戏的常见要点:企业做产品的4方面产出:四、决策五、俞军产品方法论,认知迭代史1)俞军12条产品军规2)产品经理职级的背后影响因素:…...

spring注解的开端(@Component替代bean标签的使用)
目录 一、介绍 1.什么是注解开发? 2.Spring注解的版本 3.基于spring注解的应用 4. Component的细分注解 5.相关注解 二、简单例子讲解 1.类打注解 2.扫描注解放入工厂 3.总工厂取注解调用 4.运行结果 总结: 一、介绍 1.什么是注解开发&…...
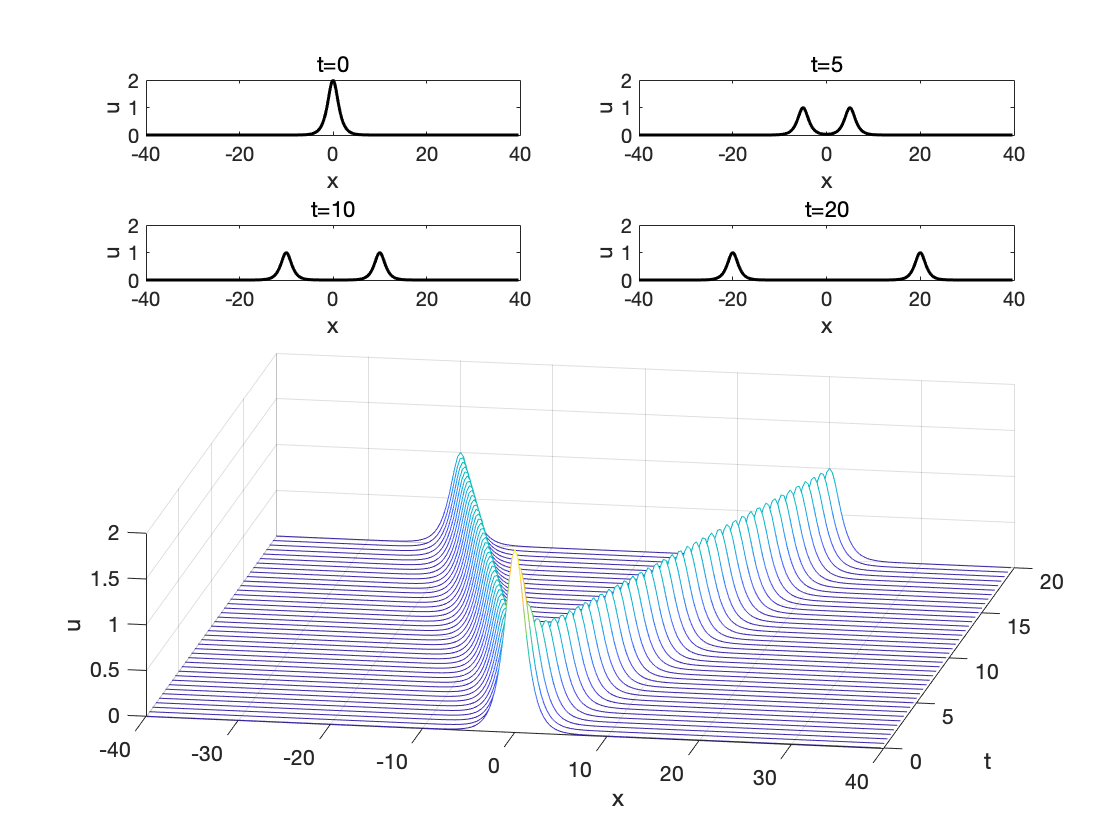
Matlab傅里叶谱方法求解一维波动方程
傅里叶谱方法求解基本偏微分方程—一维波动方程 一维波动方程 对于一根两端固定、没有受到任何外力的弦, 若只研究其中的一段, 在不太长的时间 里, 固定端来不及对这段弦产生影响, 则可以认为固定端是不存在的, 弦的长度为无限大。 这种无界 (−∞<x<∞)(-\infty<x&…...
函数典型例题)
py3中 collections.Counter()函数典型例题
文章目录py3中 collections 的常用STL**Counter()** 函数**defaultdict()** 函数**deque()** 函数**orderedDict()** 函数(缺例题)小结py3中 collections 的常用STL 对于这个工具包非常好用,尤其是其中的 Counter() 函数 使用次数颇为频繁&a…...

Linux部署达梦数据库超详细教程
陈老老老板🦸👨💻本文专栏:国产数据库-达梦数据库👨💻本文简述:本文讲一下达梦数据库的下载与安装教程(Linux版),超级详细。👨💻…...

ctfshow 每周大挑战 极限命令执行
《简单的命令执行题目》 这里感叹一下,g4佬是真好厉害,这次题目十分的难,嗯,对我这种菜鸡来说是这样的,想了一天,最后结束了,也还是没有想明白第五题的解法,我真是fw,到最…...

使用vue3,vite,less,flask,python从零开始学习硅谷外卖(16-40集)
严正声明! 重要的事情说一遍,本文章仅供分享,文章和代码都是开源的,严禁以此牟利,严禁侵犯尚硅谷原作视频的任何权益,我知道学习编程的人各种各样的心思都有,但这不是你对开源社区侵权的理由&am…...

坚持就是胜利
很多朋友,可能坚持了多年的同等学力申硕考试,依然没有通过。如果你感到困惑,感到迷茫,要坚信:坚持就能胜利。有很多人跟你一样,一直坚持在路上,没有停止脚步。 生活没有你想象的那么好ÿ…...
 或者转置 intrinsic (内参)矩阵的原因)
代码中出现转置 pose (c2w,外参矩阵) 或者转置 intrinsic (内参)矩阵的原因
在代码中见到 pose(c2w),intrinsic 矩阵的转置,觉得比较奇怪。 后来想了一下为什么。下面解释一下: 用 c2w 矩阵举例子。理论上,一个 c2w 左乘上 一个相机坐标系下的点 P的坐标,能够得到该点在…...

2023 年腾讯云服务器配置价格表出炉(2核2G/2核4G/4核8G/8核16G、16核32G)
腾讯云轻量应用服务器为轻量级的云服务器,使用门槛低,按套餐形式购买,轻量应用服务器套餐自带的公网带宽较大,4M、6M、7M、10M、14M及20M套餐可选,如果是云服务器CVM这个带宽价格就要贵很多了。 1、轻量应用服务器优惠…...
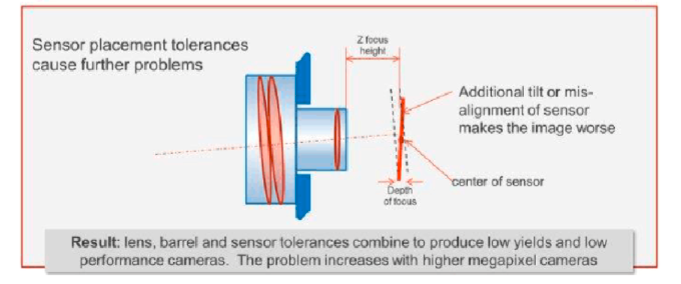
相机出图画面一半清晰,一半模糊的原因是什么?
1、问题背景:在做项目的过程中,有遇到过几次,出图后画面是一半清晰,一半模糊的现象,再重新对焦也是一样。但换了个镜头后就好了,这应该是镜头的质量问题,但导致镜头出现这种问题的具体原因是什么…...
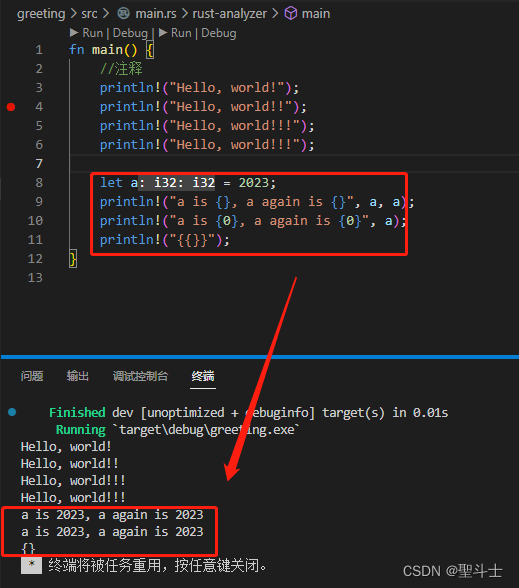
Rust学习入门--【4】Rust 输出到命令行
Rust 语言中的打印“函数” 学习新的编程语言时,大家都喜欢打印“Hello World”。 在Rust中怎样将字符串打印出来呢? Rust 输出文字的方式主要有两种:println!() 和 print!()。 “函数”差异说明: 这两个"函数"都是向…...

Vector刷写方案—vFlash工具介绍
我是穿拖鞋的汉子,魔都中坚持长期主义的工科男! 今天魔都天气是连阴雨,滴滴答答的下个不停,心情也跟着潮湿起来!老规矩分享一段喜欢的文字,避免成为高知识低文化的工程师: 即使在真正的困境里,也一直提示自己,每次自恋不得超过十分钟! 那些看似无法度过得困境,不是…...
》)
【阶段总结】《非结构化信息分析应用与实践(筹)》
《非结构化信息分析应用与实践(筹)》Part 1.知识储备一、机器学习 1.几种常见的有监督学习算法 2.几种常见的无监督学习算法 3.数据挖掘基础知识 30 问 二、神经网络与深度学习 1.MP神经网络模型(附实例代码讲解) 2.图解LST…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

Python 高级应用10:在python 大型项目中 FastAPI 和 Django 的相互配合
无论是python,或者java 的大型项目中,都会涉及到 自身平台微服务之间的相互调用,以及和第三发平台的 接口对接,那在python 中是怎么实现的呢? 在 Python Web 开发中,FastAPI 和 Django 是两个重要但定位不…...
