【数据结构与算法】最小生成树,Prim算法,Kruskal算法 详解
最小生成树的实际应用背景。
最节省经费的前提下,在n个城市之间建立通信联络网。
Kruskal算法(基于并查集)
void init() {for (int i = 1; i <= n; i++) {pre[i] = i;}
}ll root(ll a) {ll i = a;while (pre[i] != i) {i = pre[i];}return i = pre[i];
}bool merge(ll a, ll b) {ll ra = root(a);ll rb = root(b);if (ra == rb) {return 0;}pre[ra] = rb;return 1;
}ll kruskal() {sort(edge.begin(), edge.end());init();ll sum = 0;ll cnt = 0;for (const auto e : edge) {if (merge(e.u, e.v)) {sum += e.w;cnt++;}}return sum;
}
什么图适合用Prim算法求最小生成树,什么图适合用Kruskal算法求最小生成树。
-
Prim算法:归并顶点,与边数无关,适合于稠密图,即边的数量接近于节点数量的平方。Prim算法从一个节点开始,每次都添加一条连接已选节点和未选节点的最小边,因此它更适合于边的数量较多的情况。
-
Kruskal算法:归并边,适合于稀疏图,即边的数量远小于节点数量的平方。Kruskal算法每次都添加一条当前最小的边,只要这条边不会形成环,因此它更适合于边的数量较少的情况。
图示用Prim算法及Kruskal算法求最小生成树的过程。
-
Prim算法:

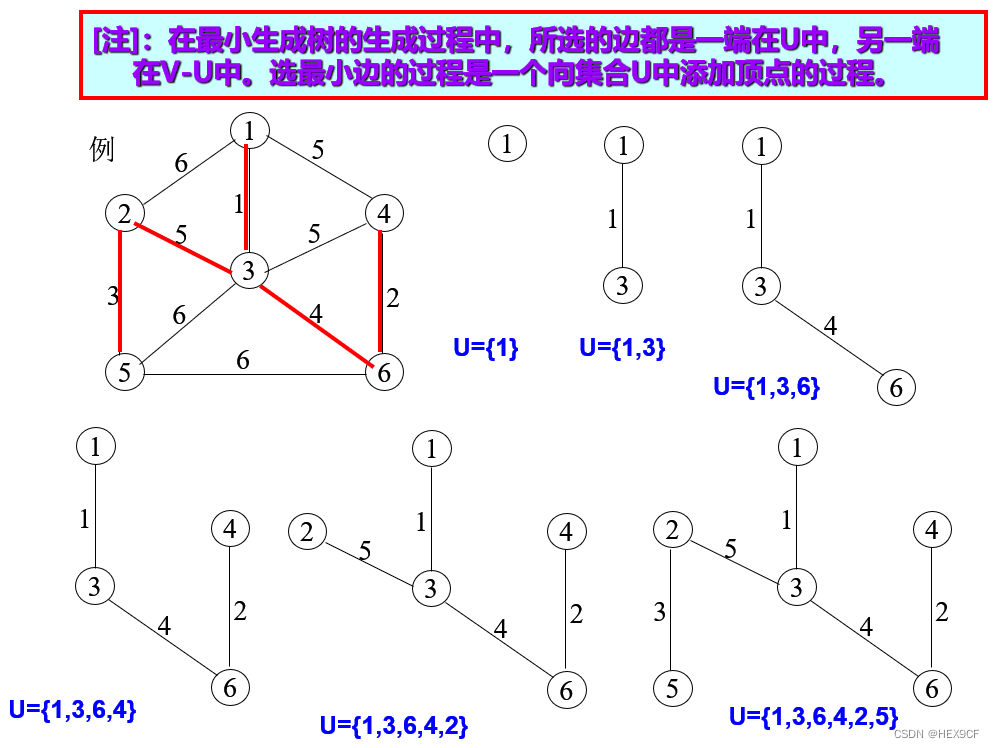
-
Kruskal算法:
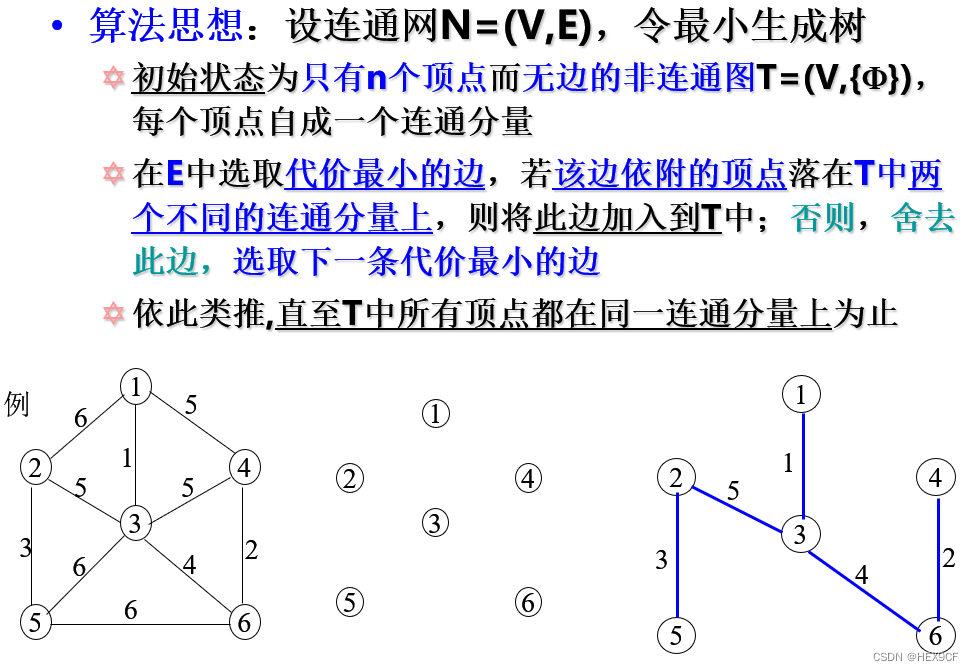
相关文章:

【数据结构与算法】最小生成树,Prim算法,Kruskal算法 详解
最小生成树的实际应用背景。 最节省经费的前提下,在n个城市之间建立通信联络网。 Kruskal算法(基于并查集) void init() {for (int i 1; i < n; i) {pre[i] i;} }ll root(ll a) {ll i a;while (pre[i] ! i) {i pre[i];}return i p…...

【启明智显产品分享】Model3工业级HMI芯片详解系列专题(三):安全、稳定、高防护
芯片作为电子设备的核心部件,,根据不同的应用领域被分为不同等级。工业级芯片适用于工业自动化、控制系统和仪器仪表等领域,对芯片的安全、稳定、防护能力等等有着较高的要求。这些芯片往往需要具备更宽的工业温度范围,能够在更恶…...

【面试干货】Java中的四种引用类型:强引用、软引用、弱引用和虚引用
【面试干货】Java中的四种引用类型:强引用、软引用、弱引用和虚引用 1、强引用(Strong Reference)2、软引用(Soft Reference)3、弱引用(Weak Reference)4、虚引用(Phantom Reference…...

对称/非对称加密
对称加密和非对称加密是两种主要的加密方式,用于保护数据的机密性和完整性。它们在密钥的使用和管理上有着显著的不同。 对称加密 原理 对称加密(Symmetric Encryption)使用相同的密钥进行加密和解密。这意味着发送方和接收方必须共享相同…...

DDei在线设计器-API-DDeiSheet
DDeiSheet DDeiSheet是代表一个页签,一个页签含有一个DDeiStage用于显示图形。 DDeiSheet实例包含了一个页签的所有数据,在获取后可以通过它访问其他内容。DDeiFile中的sheets属性记录了当前文件的页签列表。 一个DDeiFile实例至少包含一个DDeiSheet…...

随想录 Day 69 并查集 107. 寻找存在的路径
随想录 Day 69 并查集 107. 寻找存在的路径 理论基础 int n 1005; // n根据题目中节点数量而定,一般比节点数量大一点就好 vector<int> father vector<int> (n, 0); // C里的一种数组结构// 并查集初始化 void init() {for (int i 0; i < n; i)…...
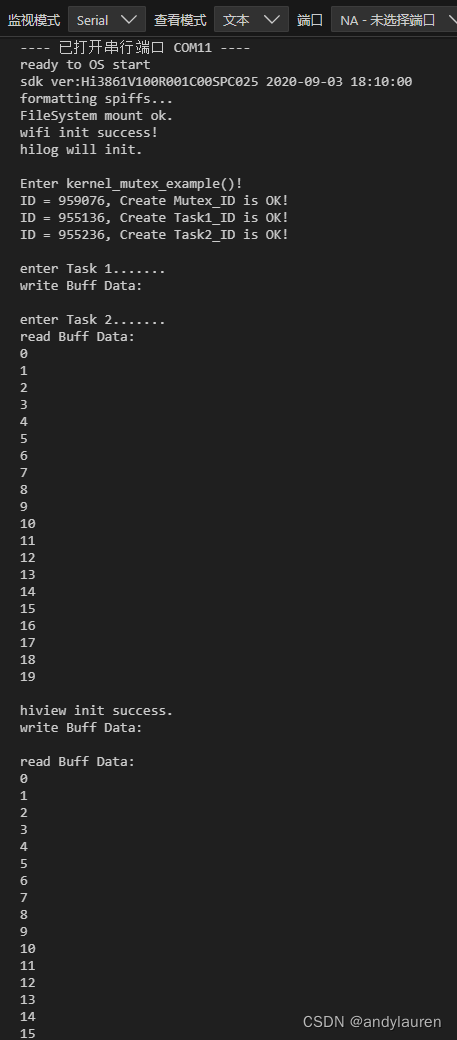
Hi3861 OpenHarmony嵌入式应用入门--LiteOS Mutex
CMSIS 2.0接口中的Mutex(互斥锁)是用于在多线程环境中保护共享资源的访问机制。Mutex(互斥锁)是一种特殊的信号量,用于确保同一时间只有一个线程可以访问特定的共享资源。 在嵌入式系统或多线程应用中,当多…...

使用STM32F103完成基于I2C协议的AHT20温湿度传感器的数据采集
文章目录 一、什么是“软件I2C”和“硬件I2C”1.1 什么是“软件I2C”1.2 什么是“硬件I2C” 二、软件I2C和硬件I2C2.1 软件模拟2.2硬件I2C 三、配置STM32CubeMX四、配置keil代码4.1 创建文件4.2 复制文件4.3 在keil中添加文件4.4 添加路径4.5 代码修改 五、硬件连接六、总结 一…...

Huffman树——AcWing 148. 合并果子
目录 Huffman树 定义 运用情况 注意事项 解题思路 AcWing 148. 合并果子 题目描述 运行代码 代码思路 其它代码 代码思路 Huffman树 定义 它是一种最优二叉树。通过构建带权路径长度最小的二叉树,经常用于数据压缩等领域。 运用情况 在数据压缩中&a…...
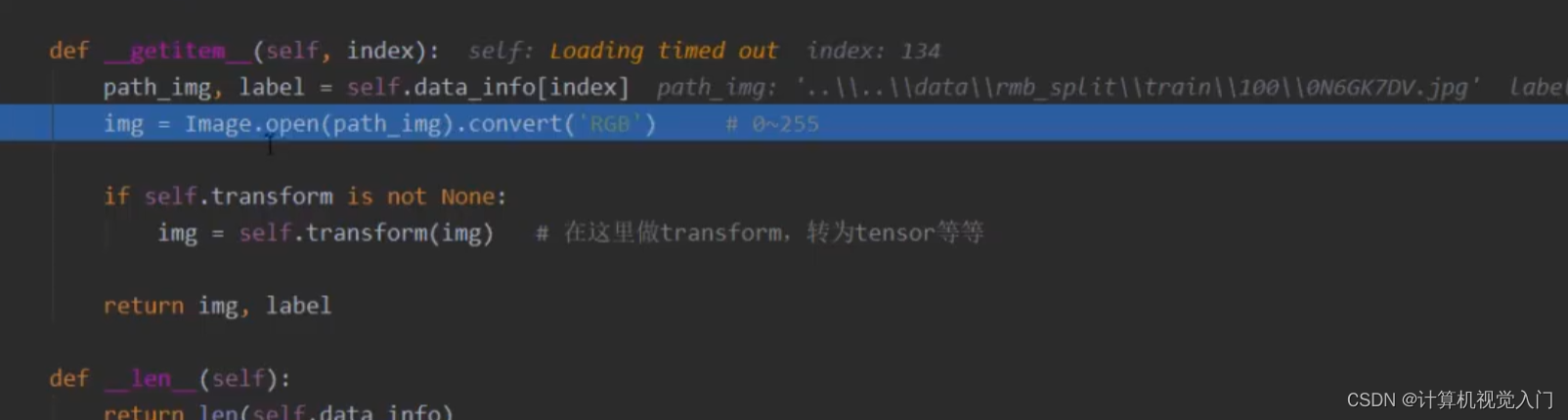
05 Pytorch 数据读取 + 二分类模型
05 Pytorch 数据读取 二分类模型05 Pytorch 数据读取 二分类模型05 Pytorch 数据读取 二分类模型 01 数据读取 DataLoader(set作为参数) 02 Dataset 从哪读,怎么读? 功能:数据从哪里读取? 如何读取…...

数据仓库之Kappa架构
Kappa架构是一种简化的数据处理架构,旨在处理实时数据流,解决传统Lambda架构中批处理和实时处理的复杂性。Kappa架构完全基于流处理,不区分批处理和实时处理,所有数据都是通过流处理系统进行处理。以下是对Kappa架构的详细介绍&am…...
Metro)
ReactNative进阶(二十八)Metro
文章目录 一、前言二、Metro生命周期2.1 解析(Resolution)2.2 转换(Transformation)2.3 序列化(Serialization) 三、拓展阅读 一、前言 众所周知,Metro 是 React Native 默认的 JavaScript 打包模块。对于前端项目,打包工具已有webpack(大而全ÿ…...

python爬虫入门到精通路线
当谈及Python爬虫从入门到精通的路线时,我们可以将其分为几个关键阶段,每个阶段都有其特定的学习目标和内容。以下是一个清晰的路线规划: 1. 入门阶段 基础知识 学习Python的基础语法、数据类型、控制流等。了解基本的网络协议(…...
Java 笔记:常见正则使用
文章目录 Java 笔记:常见正则使用正则简介常用匹配年月日的时间匹配手机号码校验 参考文章 Java 笔记:常见正则使用 正则简介 正则表达式定义了字符串的模式。 正则表达式可以用来搜索、编辑或处理文本。 正则表达式并不仅限于某一种语言,但…...
vue 2.0项目中使用tinymce富文本框遇到的问题
安装Tinymce 现在tinymce-vue最新版本是4.0,用的vue3.0的了,所以搭建的vue2.0项目要使用之前的版本 ( 安装指定版本 ). 首先安装tinymce的vue组件,因为没有注册服务 npm install tinymce/tinymce-vue2.0.0 -S接着安装tinymce: npm install…...
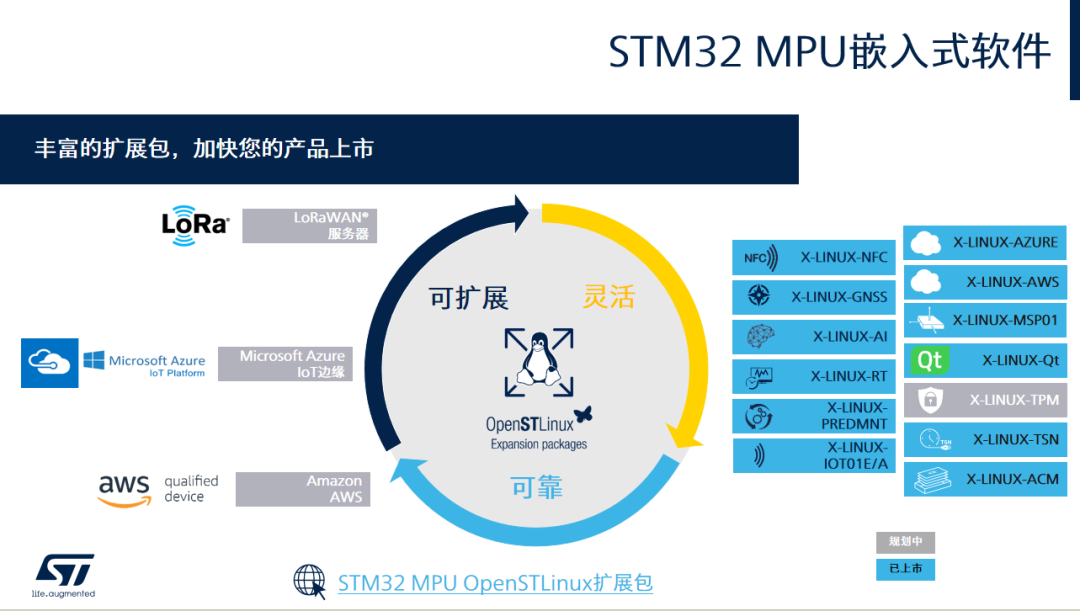
【STM32+FPGA】先进算力+强安全+边缘AI,64位STM32MP2聚焦工业4.0应用
工业应用数字化和智能化程度,是衡量新质生产力的重要标准。STM32最新一代64位微处理器STM32MP2凭借先进算力、丰富接口和高安全性,为高性能和高度互联的工业4.0应用赋能。 STM32MP2四大关键特性,为工业4.0应用赋能 STM32MP2系列的第一颗产品S…...
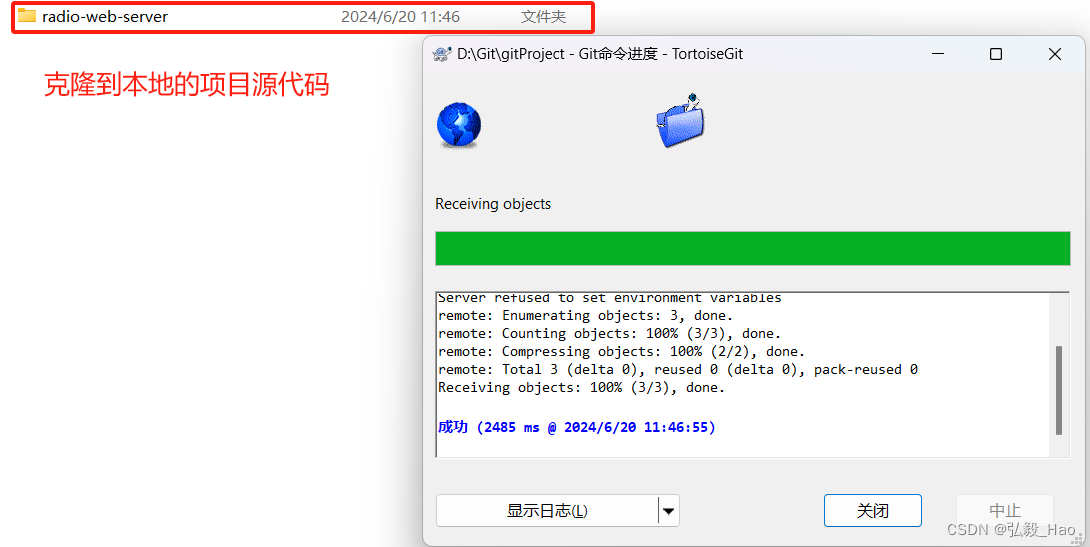
Git 和 TortoiseGit 安装和配置(图文详解)
使用git,需要在Windows上需要安装两个软件:1)Git 2)TortoiseGit 若需要,可以下载TortoiseGit汉化语言包。 注意:tortoiseGit是在安装了Git的基础上运行的,所以需要先安装Git,后安装…...

OpenAI CTO谈GPT-5将达博士生智力水平;斯坦福评估排名前十两款来自中国
🦉 AI新闻 🚀 OpenAI CTO谈GPT-5将达博士生智力水平 摘要:美国达特茅斯工程学院采访了OpenAI首席技术官米拉・穆拉蒂,她表示GPT-4的智力相当于高中生,而GPT-5将在一年半后发布,预计达到博士生水平。穆拉蒂…...

焦化超低排平台组成部分
焦化行业作为重工业的重要组成部分,其环保问题一直备受关注。近年来,随着环保意识的提升和技术的不断进步,朗观视觉焦化超低排平台应运而生,成为推动焦化行业绿色发展的重要力量。本文将深入剖析焦化超低排平台的组成部分…...

鸿蒙 navigation路由跳转,页面struct 下的生命周期、onShow、onHidden等不会触发问题
经常用安卓思维考虑问题,用习惯了Router方式跳转,但是官方推荐用 navigation,当然它有它的有点, 也有小瑕疵,用了api11 后 发现 navigation路由跳转 ,只要被它包裹的跳转到下页面的,有些生命周期…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

wpf在image控件上快速显示内存图像
wpf在image控件上快速显示内存图像https://www.cnblogs.com/haodafeng/p/10431387.html 如果你在寻找能够快速在image控件刷新大图像(比如分辨率3000*3000的图像)的办法,尤其是想把内存中的裸数据(只有图像的数据,不包…...
