当前位置： 首页 > news >正文

【Android面试八股文】Kotlin内置标准函数apply的原理是什么？

news 2025/9/16 20:46:08

文章目录

  • 一、原理解析
  • 二、 示例代码
    • 2.1 具体示例
      • 应用场景
    • 2.2 为什么使用 `apply`？

apply 是 Kotlin 标准库中的一个高阶函数，它的作用是在对象上执行一个代码块，并返回这个对象本身。其原理涉及到函数类型和接收者对象的结合使用。

一、原理解析

  1. 函数类型与接收者对象的结合：

    • apply 函数的声明如下：
      inline fun <T> T.apply(block

相关文章：

【Android面试八股文】Kotlin内置标准函数apply的原理是什么？

文章目录 一、原理解析二、 示例代码2.1 具体示例应用场景2.2 为什么使用 `apply`？apply 是 Kotlin 标准库中的一个高阶函数，它的作用是在对象上执行一个代码块，并返回这个对象本身。其原理涉及到函数类型和接收者对象的结合使用。 一、原理解析 函数类型与接收者对象的结合…...

编程日记 2024/6/24 18:05:17

RegionClip环境安装踩坑指南

RegionClip环境安装 RegionClip环境安装)问题1问题2问题3问题4问题5 RegionClip环境安装) 特别强调&#xff0c;不要单独去安装detectron2&#xff0c;会出现model.clip不存在的错误&#xff0c;通过python -m pip install -e RegionCLIP就可以问题1 问题&#xff1a;torch-c…...

编程日记 2024/6/24 18:03:15

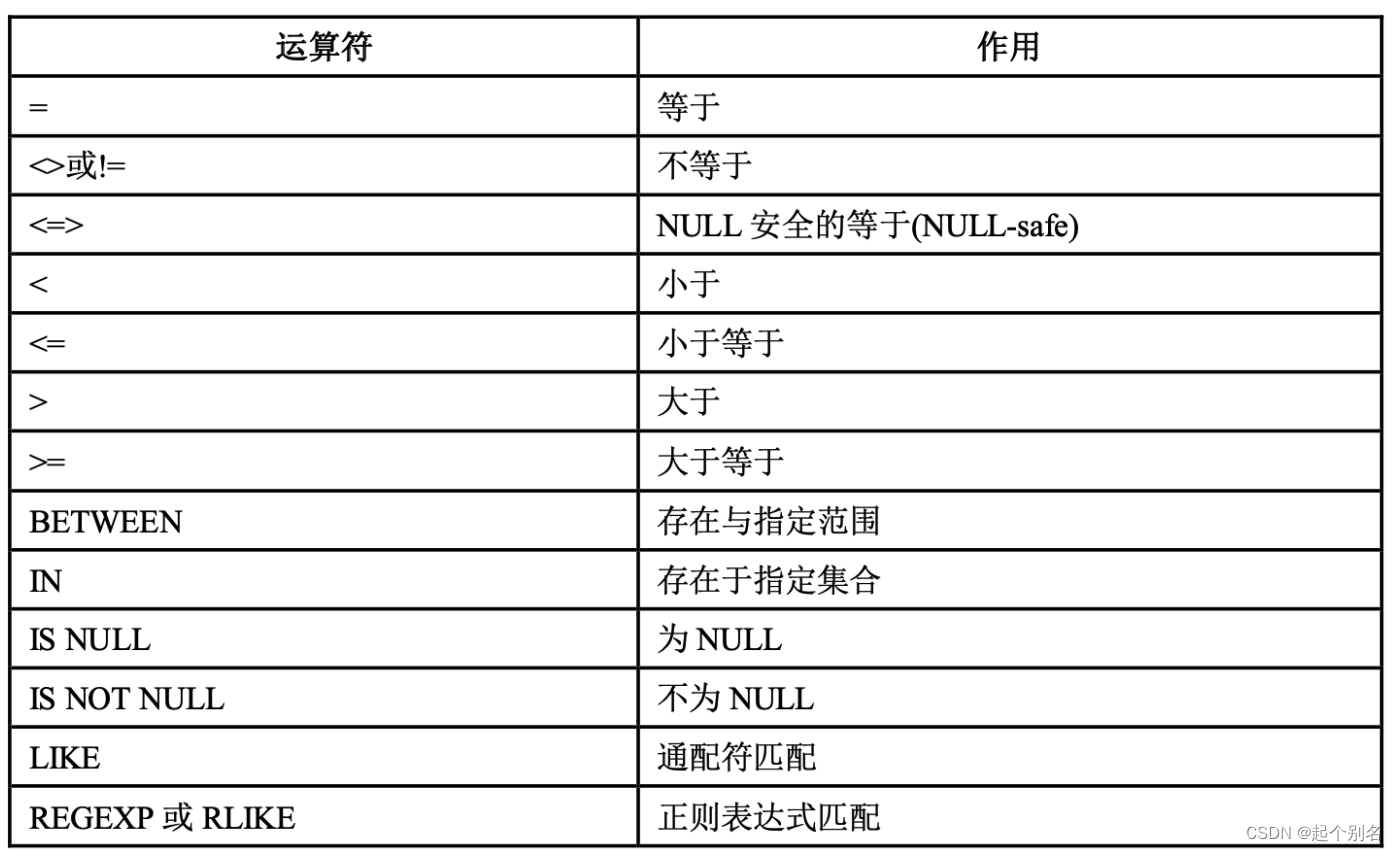
MySQL数据类型、运算符以及常用函数

MySQL数据类型 MySQL数据类型定义了数据的大小范围&#xff0c;因此使用时选择合适的类型&#xff0c;不仅会降低表占用的磁盘空间&#xff0c; 间接减少了磁盘I/O的次数&#xff0c;提高了表的访问效率&#xff0c;而且索引的效率也和数据的类型息息相关。 数值类型 浮点类型…...

编程日记 2024/6/24 18:00:11

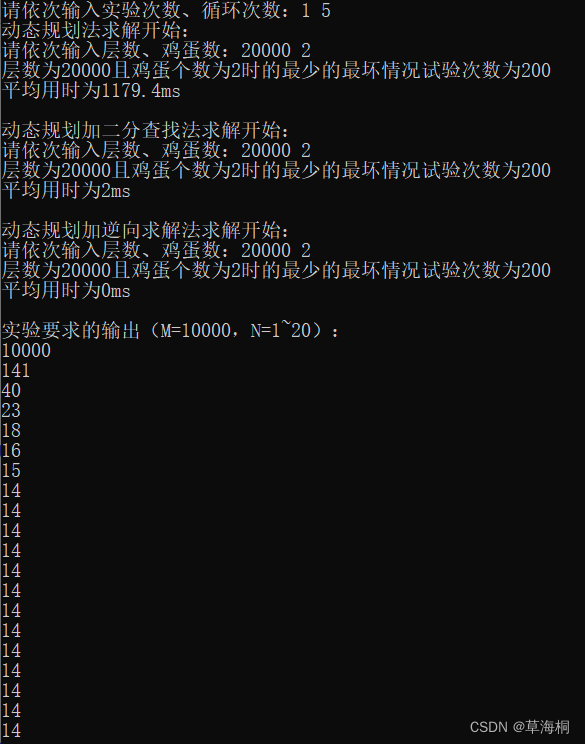
算法设计与分析：动态规划法求扔鸡蛋问题 C++

目录 一、实验目的 二、问题描述 三、实验要求 四、算法思想和实验结果 1、动态规划法原理&#xff1a; 2、解决方法&#xff1a; 2.1 方法一&#xff1a;常规动态规划 2.1.1 算法思想&#xff1a; 2.1.2 时间复杂度分析 2.1.3 时间效率分析 2.2 方法二&#xff1a;动态规划加…...

编程日记 2024/6/24 17:59:10

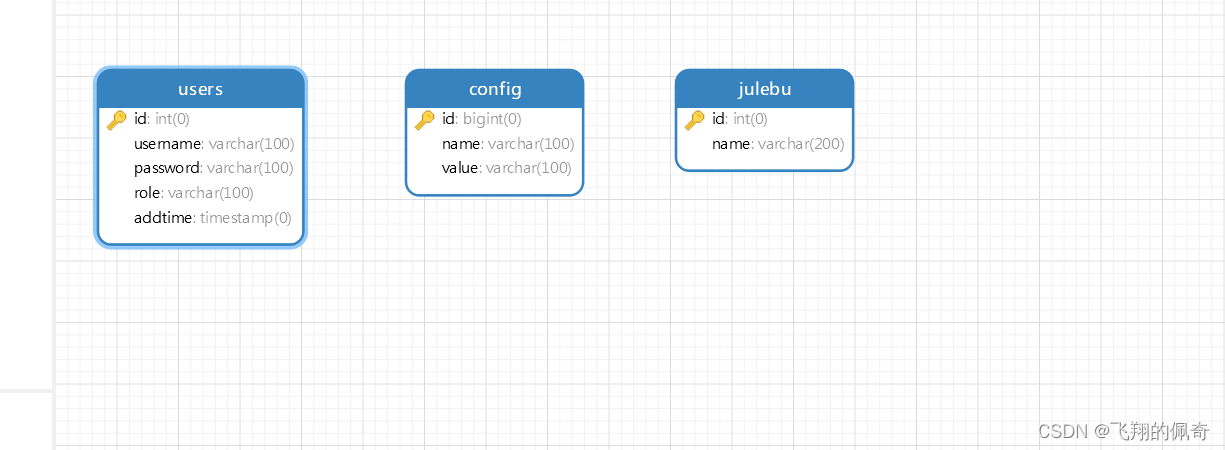
Java项目：基于SSM框架实现的电子竞技管理平台【ssm+B/S架构+源码+数据库+毕业论文】

一、项目简介 本项目是一套基于SSM框架实现的电子竞技管理平台 包含&#xff1a;项目源码、数据库脚本等&#xff0c;该项目附带全部源码可作为毕设使用。 项目都经过严格调试&#xff0c;eclipse或者idea 确保可以运行&#xff01; 该系统功能完善、界面美观、操作简单、功能…...

编程日记 2024/6/24 17:58:09

Scala入门介绍

Scala 是一种强大的多范式编程语言&#xff0c;旨在融合面向对象编程和函数式编程的特性。它运行在 Java 虚拟机&#xff08;JVM&#xff09;上&#xff0c;因此可以无缝地与 Java 库进行交互。以下是对 Scala 的入门介绍&#xff0c;并附带了一些基本代码示例。 环境设置 首先…...

编程日记 2024/6/24 17:56:06

品牌策划背后的秘密：我为何对此工作情有独钟？

你是否曾有过一个梦想&#xff0c;一份热爱&#xff0c;让你毫不犹豫地投身于一个行业&#xff1f; 我就是这样一个对品牌策划充满热情的人。 从选择职业到现在&#xff0c;我一直在广告行业里“混迹”&#xff0c;一路走来&#xff0c;也见证了许多对品牌策划一知半解的求职…...

编程日记 2024/6/24 17:55:04

超越招聘技术人才目标的最佳技术招聘统计数据

研究发现&#xff0c;难以找到的人才比以往任何时候都更难找到&#xff1a;根据新人才委员会招聘调查报告&#xff1a;2024年难以找到的人才的战略和战略&#xff0c;60%的受访者表示&#xff0c;熟练人才的招聘时间比一年前长。调查进一步揭示了以下关于招聘技术的关键事实&am…...

编程日记 2024/6/24 17:53:00

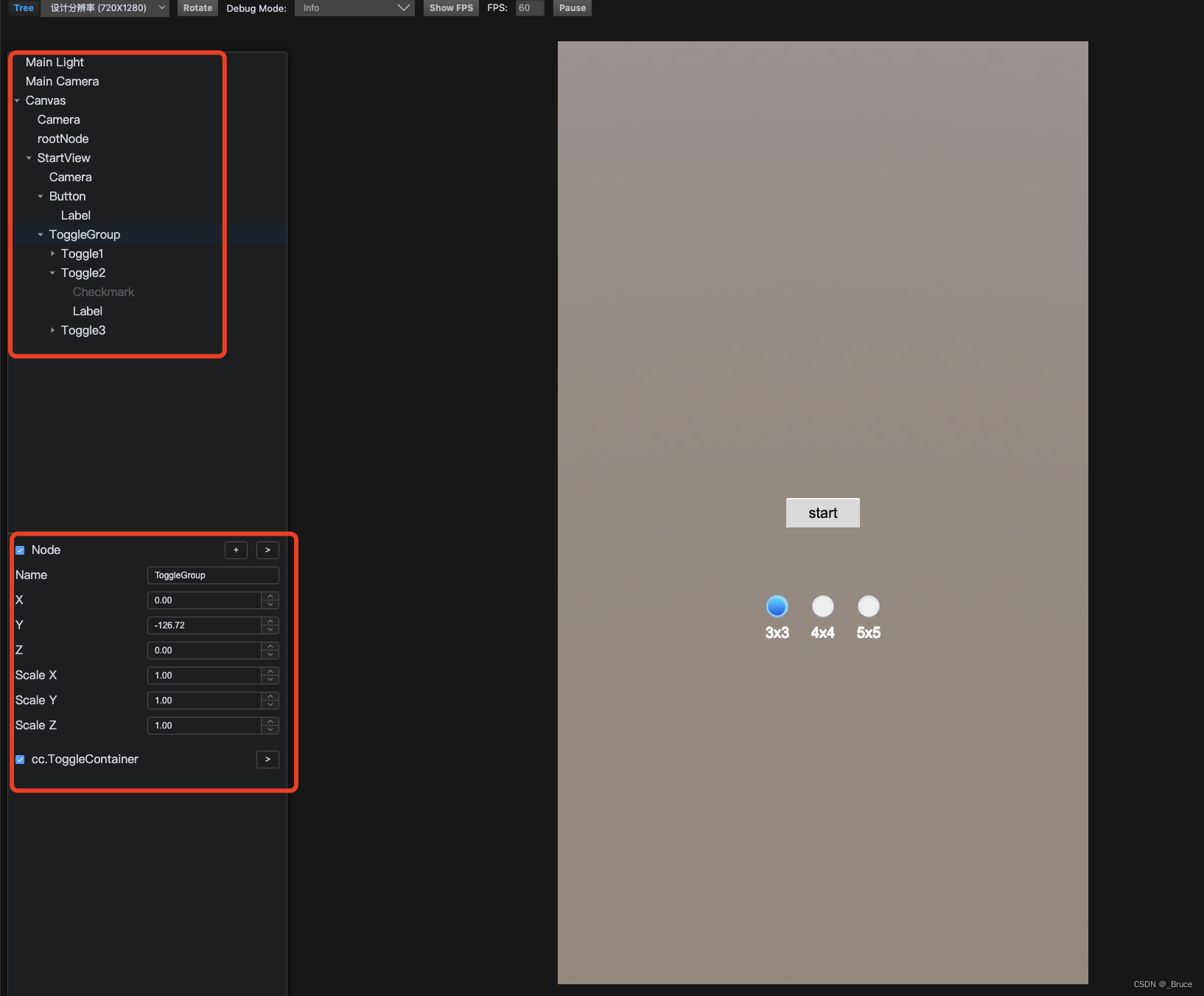
cocos creator 调试插件

适用 Cocos Creator 3.4 版本&#xff0c;cocos creator 使用google浏览器调试时&#xff0c;我们可以把事实运行的节点以节点树的形式显示在浏览器上&#xff0c;支持运行时动态调整位置等、、、 将下载的preview-template插件解压后放在工程根目录下&#xff0c;然后重新运行…...

编程日记 2024/6/24 17:51:55

Clickhouse监控_监控的指标以及Grafana配置Clickhouse指标异常时触发报警

使用PrometheusGrafana来监控Clickhouse服务和性能指标 Clickhouse监控指标的官方文档https://clickhouse.com/docs/zh/operations/monitoring 建议使用PrometheusGrafana组合监控Clickhouse服务和性能指标&#xff0c;数据流向&#xff1a;Prometheus的clickhouse_exporter组件…...

编程日记 2024/6/24 17:50:53

动手学深度学习（Pytorch版）代码实践 -卷积神经网络-27含并行连结的网络GoogLeNet

27含并行连结的网络GoogLeNet import torch from torch import nn from torch.nn import functional as F import liliPytorch as lp import matplotlib.pyplot as pltclass Inception(nn.Module):# c1--c4是每条路径的输出通道数def __init__(self, in_channels, c1, c2, c3, …...

编程日记 2024/6/24 17:49:49

fastadmin多语言切换设置

fastadmin版本&#xff1a;1.4.0.20230711 以简体&#xff0c;繁体&#xff0c;英文为例 一&#xff0c;在application\config.php 里开启多语言 // 是否开启多语言lang_switch_on > true, // 允许的语言列表allow_lang_list > [zh-cn, en,zh-tw], 二…...

编程日记 2024/6/24 17:48:46

如何清理docker build的缓存

在使用 Docker 构建镜像时&#xff0c;Docker 会利用构建缓存来加速后续的构建过程。如果某一层及其所有上层未发生变化&#xff0c;Docker 就会重用这一层的缓存。虽然这可以显著提升构建速度&#xff0c;但有时你可能希望强制 Docker 忽略缓存&#xff0c;以确保从头开始重新…...

编程日记 2024/6/24 17:44:42

OceanBase v4.2 特性解析：如何用分页保序功能解决MySQL模式分页查询不稳定

导言 在MySQL业务迁移OceanBase过程中&#xff0c;经常遇到的一个问题是分页查询结果的不稳定性&#xff0c;这通常需要数据库DBA介入绑定执行计划。下面简单举个例子&#xff0c;以便大家更好地理解为什么有的分页查询&#xff0c;在原来的MySQL数据库下运行没有问题&#xf…...

编程日记 2024/6/24 17:43:26

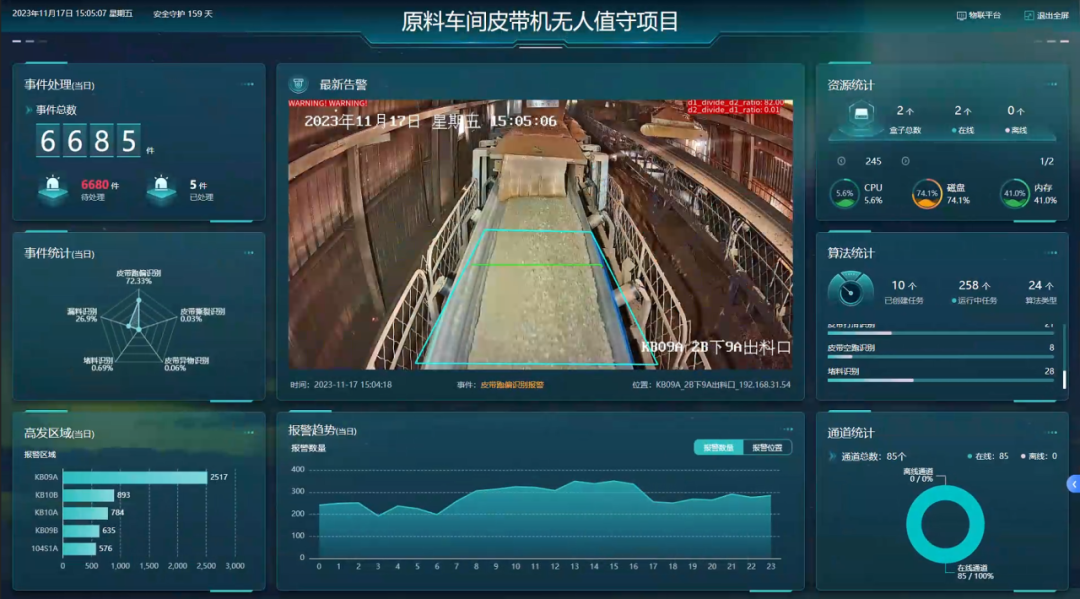
RK3588/算能/Nvidia智能盒子：加速山西铝业智能化转型，保障矿业皮带传输安全稳定运行

近年来&#xff0c;各类矿山事故频发&#xff0c;暴露出传统矿业各环节的诸多问题。随着全国重点产煤省份相继出台相关政策文件&#xff0c;矿业智能化建设进程加快。皮带传输系统升级是矿业智能化的一个重要环节&#xff0c;同时也是降本增效的一个重点方向。 △各省份智能矿山…...

编程日记 2024/6/24 17:38:17

2024.6.24 IDEA中文乱码问题（服务器 控制台 TOMcat）实测已解决

1.问题产生原因&#xff1a; 1.文件编码不一致&#xff1a;如果文件的编码方式与IDEA设置的编码方式不一致&#xff0c;就会产生乱码。确保文件和IDEA使用相同的编码&#xff0c;通常是UTF-8。2.IDEA设置问题&#xff1a;检查IDEA的全局编码设置和项目编码设置是否正确。3.终端…...

编程日记 2024/6/24 17:37:11

桌面编辑器ONLYOFFICE 功能多样性快来试试吧！

目录 ONLYOFFICE 桌面编辑器 8.1 ONLYOFFICE介绍 主要功能和特点 使用场景 1.PDF编辑器 2.幻灯片版式 3.编辑&#xff0c;审阅和查看模式 4.隐藏连接到云版块 5.RTL语言支持和本地化选项 6.媒体播放器 7、其他新功能 8.下载 总结 ONLYOFFICE 桌面编辑器 8.1 官网地…...

编程日记 2024/6/24 17:36:10

三维渲染中的散光圆

三维渲染中的散光圆 散光圆&#xff08;Circle of Confusion&#xff0c;CoC&#xff09;是三维渲染和摄影中的一个重要概念&#xff0c;尤其在景深&#xff08;Depth of Field&#xff0c;DoF&#xff09;效果的生成中起着关键作用。它描述了在成像过程中&#xff0c;焦点前后…...

编程日记 2024/6/24 17:35:06

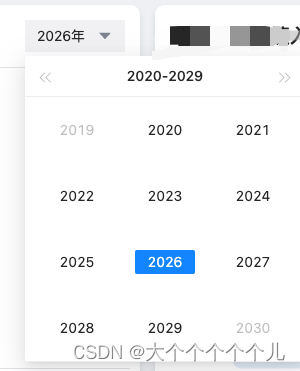
Vue3 + Ant-Design 中 a-date-picke 实现选择切换年份 没有鼠标光标，输入框内自带‘年’

效果图&#xff1a; 效果图 <a-date-picker ref"datePicker" v-model:value"year" picker"year" value-format"YYYY年" format"YYYY年" :bordered"false" :allowClear"false" inputReadOnly change&…...

编程日记 2024/6/24 17:34:02

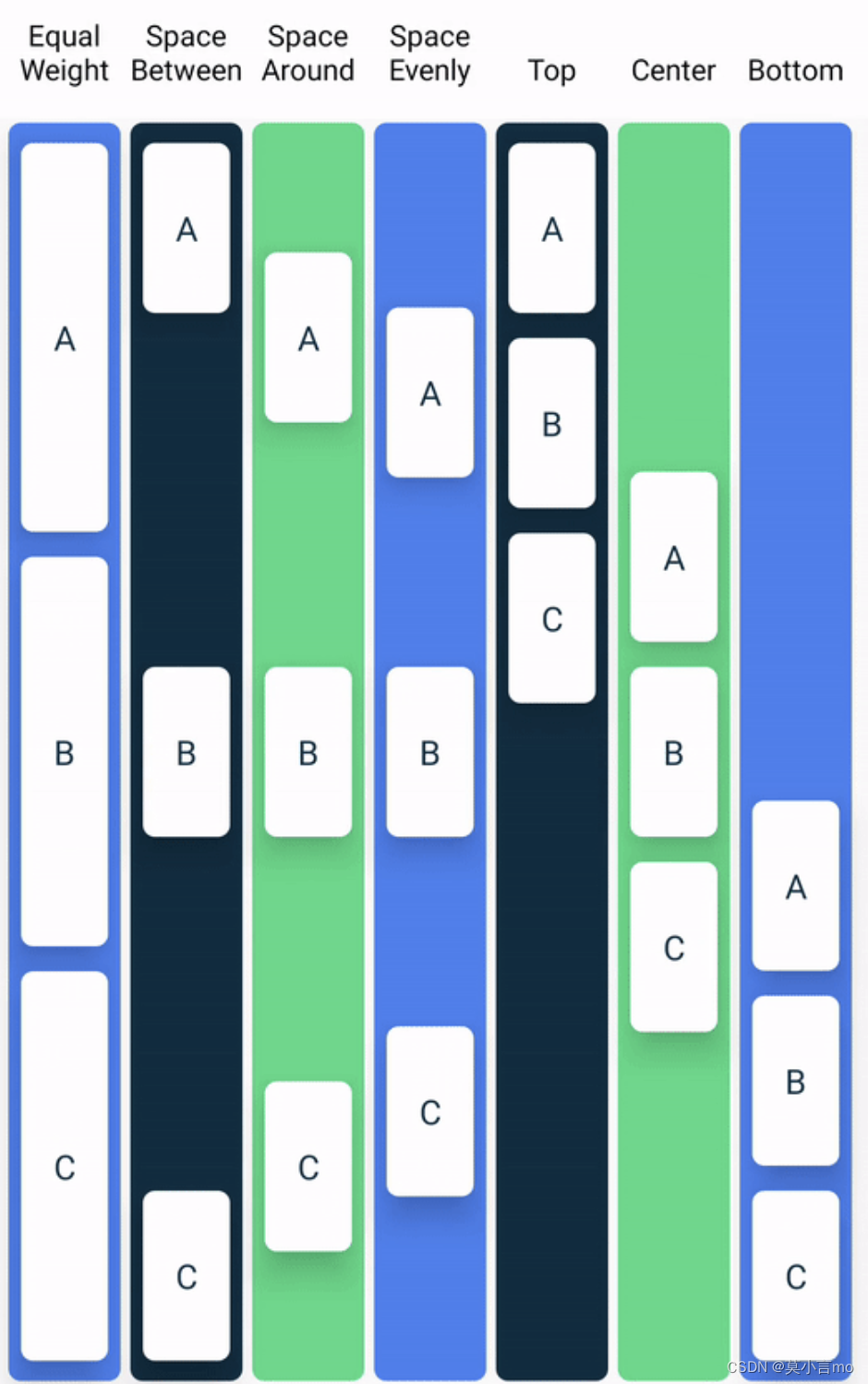
Jetpack Compose_Alignment对其+Arrangement排列

文章目录 1.Alignment 对齐1.1Alignment 对齐方式1.2AbsoluteAlignment 绝对对齐1.3BiasAlignment 偏差对齐1.4BiasAbsoluteAlignment偏差绝对对齐 2.Arrangement 排列2.1Arrangement 排列方式2.2Arrangement.Horizontal2.3Arrangement.Vertical 1.Alignment 对齐 1.1Alignmen…...

编程日记 2024/6/24 17:32:58

HTML 语义化

目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案&#xff1a; 语义化标签&#xff1a; <header>&#xff1a;页头<nav>&#xff1a;导航<main>&#xff1a;主要内容<article>&#x…...

编程新知 2025/8/7 7:40:03

pam_env.so模块配置解析

在PAM&#xff08;Pluggable Authentication Modules&#xff09;配置中&#xff0c; /etc/pam.d/su 文件相关配置含义如下&#xff1a; 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块&#xff0c;负责验证用户身份&am…...

编程新知 2025/8/21 21:33:01

Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！

一、引言 在数据驱动的背景下&#xff0c;知识图谱凭借其高效的信息组织能力&#xff0c;正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合&#xff0c;探讨知识图谱开发的实现细节&#xff0c;帮助读者掌握该技术栈在实际项目中的落地方法。 …...

编程新知 2025/9/11 9:34:44

k8s业务程序联调工具-KtConnect

概述 原理 工具作用是建立了一个从本地到集群的单向VPN&#xff0c;根据VPN原理&#xff0c;打通两个内网必然需要借助一个公共中继节点&#xff0c;ktconnect工具巧妙的利用k8s原生的portforward能力&#xff0c;简化了建立连接的过程&#xff0c;apiserver间接起到了中继节…...

编程新知 2025/9/1 10:25:23

人工智能（大型语言模型 LLMs）对不同学科的影响以及由此产生的新学习方式

今天是关于AI如何在教学中增强学生的学习体验&#xff0c;我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育&#xff0c;这并非炒作&#xff0c;而是已经发生的巨大变革。教育机构和教育者不能忽视它&#xff0c;试图简单地禁止学生使…...

编程新知 2025/9/5 8:48:52

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)

前言&#xff1a; 双亲委派机制对于面试这块来说非常重要&#xff0c;在实际开发中也是经常遇见需要打破双亲委派的需求&#xff0c;今天我们一起来探索一下什么是双亲委派机制&#xff0c;在此之前我们先介绍一下类的加载器。 目录 ​编辑 前言&#xff1a; 类加载器 1. …...

编程新知 2025/9/14 14:00:12

Chrome 浏览器前端与客户端双向通信实战

Chrome 前端&#xff08;即页面 JS / Web UI&#xff09;与客户端&#xff08;C 后端&#xff09;的交互机制&#xff0c;是 Chromium 架构中非常核心的一环。下面我将按常见场景&#xff0c;从通道、流程、技术栈几个角度做一套完整的分析&#xff0c;特别适合你这种在分析和改…...

编程新知 2025/9/7 8:49:16

comfyui 工作流中 图生视频 如何增加视频的长度到5秒

comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗&#xff1f; 在ComfyUI中实现图生视频并延长到5秒&#xff0c;需要结合多个扩展和技巧。以下是完整解决方案&#xff1a; 核心工作流配置&#xff08;24fps下5秒120帧&#xff09; #mermaid-svg-yP…...

编程新知 2025/9/3 7:13:34

Axure 下拉框联动

实现选省、选完省之后选对应省份下的市区...

编程新知 2025/9/7 8:46:59

Python常用模块：time、os、shutil与flask初探

一、Flask初探 & PyCharm终端配置 目的： 快速搭建小型Web服务器以提供数据。 工具： 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask： 建议： 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装，避免频繁切换。 PyCharm Terminal 配置建议： 打开 Py…...

编程新知 2025/7/20 9:54:36