Jetpack Compose_Alignment对其+Arrangement排列
文章目录
- 1.Alignment 对齐
- 1.1Alignment 对齐方式
- 1.2AbsoluteAlignment 绝对对齐
- 1.3BiasAlignment 偏差对齐
- 1.4BiasAbsoluteAlignment偏差绝对对齐
- 2.Arrangement 排列
- 2.1Arrangement 排列方式
- 2.2Arrangement.Horizontal
- 2.3Arrangement.Vertical
1.Alignment 对齐
1.1Alignment 对齐方式
Alignment
| 类型 | 对齐方式 | 说明 | ||
|---|---|---|---|---|
| Alignment | TopStart | 顶部左对齐 | ||
| TopCenter | 顶部居中对齐 | |||
| TopEnd | 顶部右对齐 | |||
| CenterStart | 居中左对齐 | |||
| Center | 居中 | |||
| CenterEnd | 居中右对齐 | |||
| BottomStart | 底部左对齐 | |||
| BottomCenter | 底部居中 | |||
| BottomEnd | 底部右对齐 | |||
| Alignment.Vertical | Top | 竖直的置顶 | ||
| CenterVertically | 竖直的居中 | |||
| Bottom | 竖直的置底 | |||
| Alignment.Horizontal | Start | 水平的置左 | ||
| CenterHorizontally | 水平的居中 | |||
| End | 水平的置右 |
疑问:为什么有 Alignment 了,还需要有 Alignment.Vertical 和 Alignment.Horizontal 呢?
因为有些控件,如 Row 只能调整竖直方向上的对齐方式,水平方向上调的是 Arrangement 排列,因此对齐枚举需要限制为特定方向上的
1.2AbsoluteAlignment 绝对对齐
AbsoluteAlignment
不知道布局方向的常见对齐方式的集合。
| 类型 | 对齐方式 | 说明 | ||
|---|---|---|---|---|
| Alignment | TopLeft | 左上角 | ||
| TopRight | 右上角 | |||
| CenterLeft | 居中左侧 | |||
| CenterRight | 居中右侧 | |||
| BottomLeft | 底部左侧 | |||
| BottomRight | 底部右侧 | |||
| Alignment.Horizontal | Left | 水平方向左侧 | ||
| Right | 水平方向右侧 |
当不知道是横向还是纵向布局方式时使用,暂时还没想到应用场景。(欢迎评论补充)
1.3BiasAlignment 偏差对齐
BiasAlignment
-1: 表示 start/top
0: 表示 center
1: 表示 end/bottom
data class BiasAlignment(val horizontalBias: Float, // 水平方向对齐方式val verticalBias: Float // 竖直方向对齐方式
)
1.4BiasAbsoluteAlignment偏差绝对对齐
BiasAbsoluteAlignment
-1: 表示对齐到左上角
0: 表示居中
1: 表示右下角
就是在 左上角 到 右下角 这条斜线上对齐
data class BiasAbsoluteAlignment(private val horizontalBias: Float,private val verticalBias: Float
)
2.Arrangement 排列
2.1Arrangement 排列方式
Arrangement
| 对齐方式 | 说明 | ||
|---|---|---|---|
| Equal Weight | 等宽/高 | ||
| Space Between | 等间距 | ||
| Space Around | 每个item等padding | ||
| Space Evenly | 每个item等margin | ||
| End | 尾部对其 | ||
| Center | 居中 | ||
| Start | 头部对其 |
2.2Arrangement.Horizontal
如:Row 的 horizontalArrangement
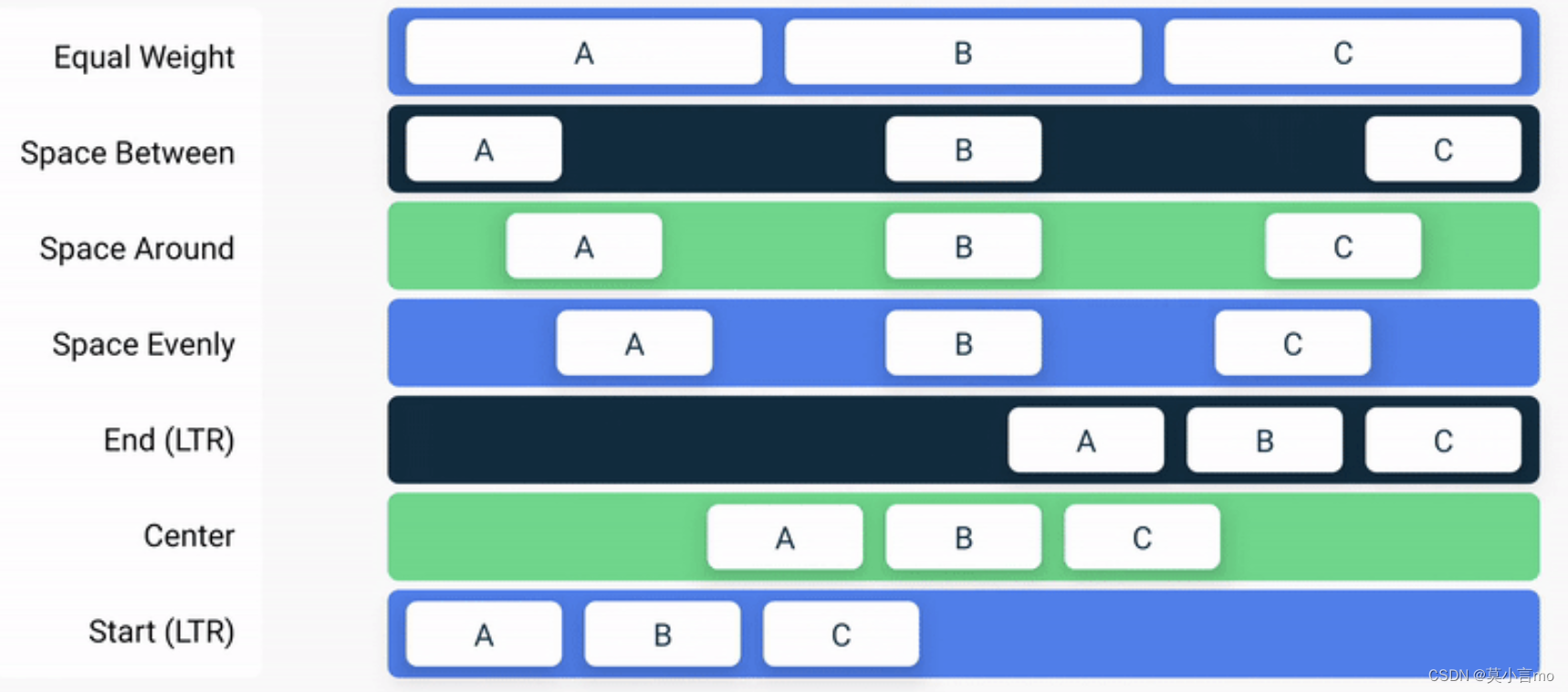
2.3Arrangement.Vertical
如:Column 的 verticalArrangement
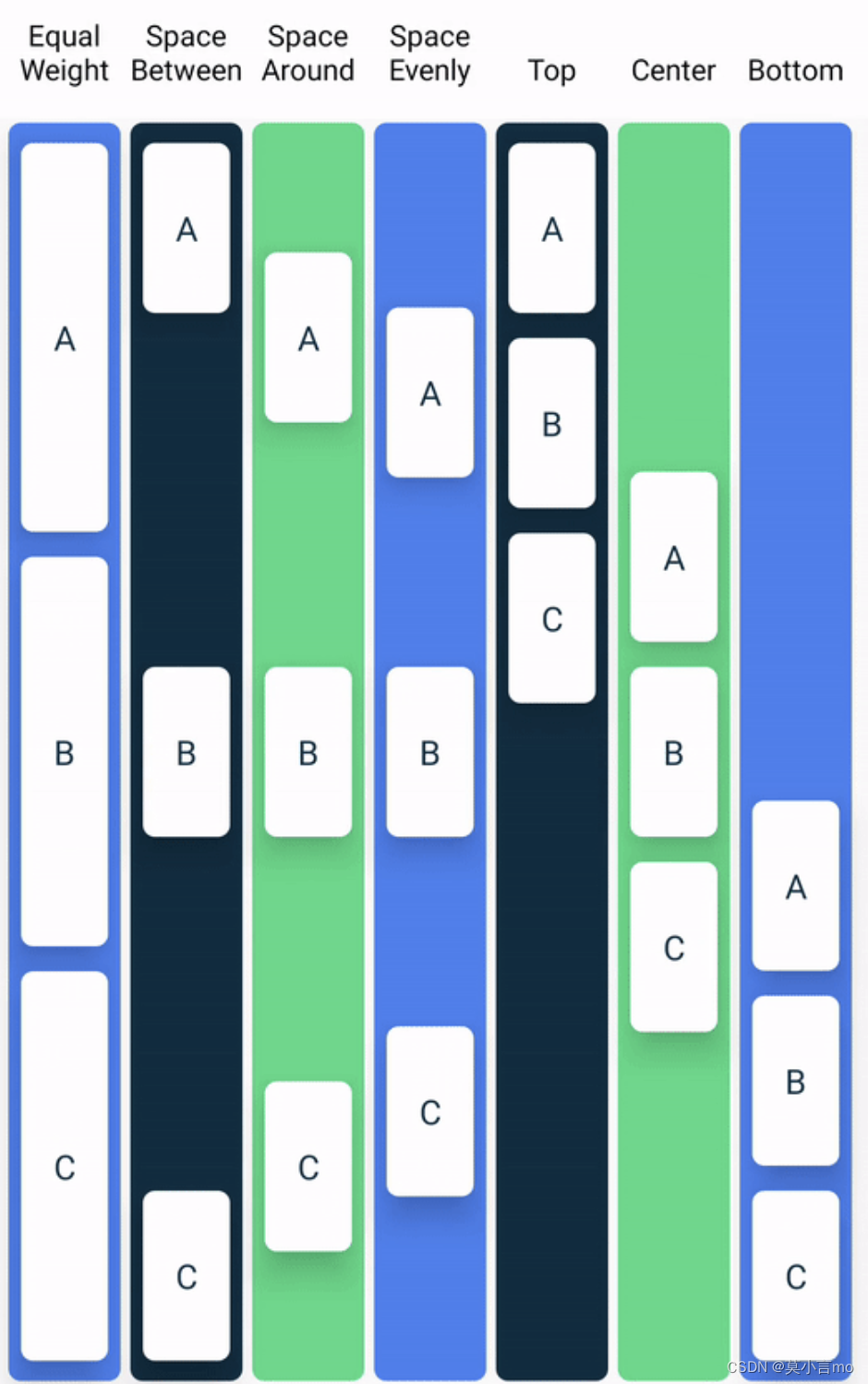
参考:
androidx.compose.foundation.layout
Componse教程 | 关于 Alignment与Arrangement
相关文章:

Jetpack Compose_Alignment对其+Arrangement排列
文章目录 1.Alignment 对齐1.1Alignment 对齐方式1.2AbsoluteAlignment 绝对对齐1.3BiasAlignment 偏差对齐1.4BiasAbsoluteAlignment偏差绝对对齐 2.Arrangement 排列2.1Arrangement 排列方式2.2Arrangement.Horizontal2.3Arrangement.Vertical 1.Alignment 对齐 1.1Alignmen…...
)
Vue进阶之Vue无代码可视化项目(五)
Vue无代码可视化项目 编排引擎smooth-dndLeftPanel.vueLayoutView.vuestores/debug.tsstores/editor.tsAppNavigator.vue添加-左侧栏添加到中间部分LayoutView.vuestore/editor.tsLeftPanel.vue移动-中间部分区域的位置更改新建文件夹utils、文件array.tsarray.tsLayoutView.vu…...

【Linux进程】Linux下的---七大进程状态(什么是进程状态?Linux下有哪些进程状态?)
目录 一、前言 二、什么是进程状态? 三、操作系统(OS)下的 --- 进程状态 🔥运行状态🔥 🔥阻塞状态🔥 🔥挂起状态🔥 四、Linux下的7种进程状态 🔥运行状态 -- R🔥…...

Linux的dev/ 和 sys/ 和 proc/ 目录
linux精神: 一切设备皆文件。 设备被抽象成文件 1、 /dev : 该目录放的设备文件,是应用程序和内核的交互文件,应用程序对这些文件的读写控制可以直接访问到实际的设备 应用程序通过mknod创建的文件,如果底层驱动对mknod的设备号…...

代码随想录算法训练营day64 | 98. 所有可达路径
图论理论基础 1、图的种类 整体上一般分为 有向图 和 无向图。 加权有向图,就是图中边是有权值的,加权无向图也是同理。 2、度 无向图中有几条边连接该节点,该节点就有几度 在有向图中,每个节点有出度和入度。出度ÿ…...
php上传zip压缩包到服务器并解压,解析压缩包内excel表格数据导入到数据库
需求: 1.需要管理后台将excel表格中的每条单词数据导入到数据库中. 2.每条单词数据对应的图片和音频文件需要上传到服务器中. 为了让客户上传数据方便,考虑了一下决定通过后台上传压缩包的方式实现 测试压缩包: 压缩包的目录结构 管理后台导入教材 public function upload…...

48-5 内网渗透 - JuicyPotato、Pipe Potato提权
Juicy Potato Juicy Potato 与 Rotten Potato(烂土豆) 的原理几乎完全相同,只是在后者的基础上做了扩展,以便更灵活地利用 Rotten Potato。Juicy Potato 不再像 Rotten Potato 那样依赖于一个现有的 Meterpreter,并且可以自定义 COM 对象加载的端口,以及根据系统版本更换…...
Windows C++ 应用软件开发从入门到精通详解
目录 1、引言 2、IDE 开发环境介绍 2.1、Visual Studio 2.2、Qt Creator 3、 C语言特性 3.1、熟悉泛型编程 3.2、了解C/C异常处理 3.3、熟练使用STL容器 3.4、熟悉C11新特性 4、Windows 平台的编程技术与调试技能 4.1、需要掌握的若干编程技术和基础知识 4.2、需…...

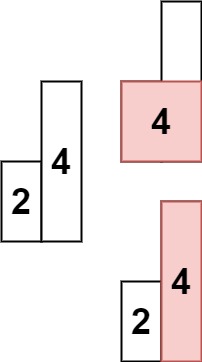
Leetcode 3195. Find the Minimum Area to Cover All Ones I
Leetcode 3195. Find the Minimum Area to Cover All Ones I 1. 解题思路2. 代码实现 题目链接:3195. Find the Minimum Area to Cover All Ones I 1. 解题思路 这一题还是挺简单的,只要找到所有1所在的元素的上下左右4个边界,作为目标矩形…...

ONLYOFFICE8.1版本桌面编辑器测评
目录 一、引言 二、界面设计:简洁大方,操作便捷 三、功能评测:全面升级,满足多样需求 四、性能评测:稳定流畅,高效运行 五、总结与展望 ONLYOFFICE官网链接:ONLYOFFICE - 企业在线办公应用…...

线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
文章目录 1. 单位矩阵的秩1变换1.1 功能说明1.2 证明 2. 单位矩阵 I n I_n In的秩k变换3. 一般矩阵A的秩k变换4. 公式用途4.1 求解方程4.2 卡曼滤波 1. 单位矩阵的秩1变换 1.1 功能说明 假设我们有一个单位矩阵I,列向量u,v那么当我们对单位向量I减去秩为1的矩阵…...

强强联合 极光推送(JPush)成为华为生态市场首家推送类SDK服务商
近日,中国领先的客户互动和营销科技服务商,极光(Aurora Mobile,纳斯达克股票代码:JG)的核心产品极光推送(JPush)顺利通过华为开发者联盟的多项测试及审核,成为首家在Harm…...

防止在 Qt 中触发信号
在 Qt 中工作时,有时我们需要暂时阻止某些信号的触发。以下是一个经典场景:我们有一个 QCheckBox 对象,当用户勾选或取消勾选时,需要调用一个函数,因此我们将这个函数连接到 stateChanged(int state) 信号。然而&#…...
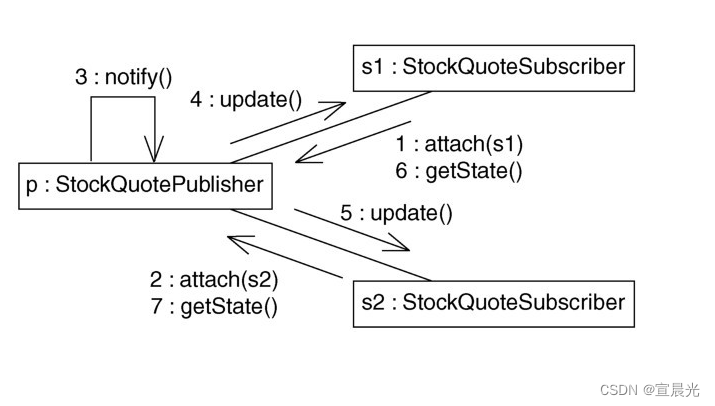
【UML用户指南】-17-对基本行为建模-交互
目录 1、消息的可视化表示 2、对象与角色 3、链和连接件 4、消息 5、序列 6、创建、修改和撤销 7、表示法 8、常用建模技术 8.1、对控制流建模 8.1.1、基于时间的控制流 8.1.2、基于结构的控制流 在任何有意义的系统中,对象都不是孤立存在的,…...

Java中的类加载器与热部署技术详解
Java中的类加载器与热部署技术详解 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在软件开发中,特别是在大型应用和服务的开发过程中,类…...
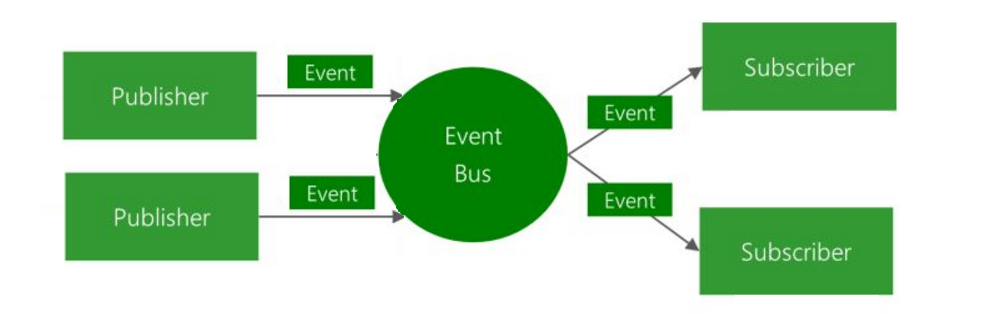
【事件总线】EventBus
文章目录 概述如何使用如何发布消息如何进行消息监听 来源 概述 事件总线是对发布-订阅模式(观察者)的一种实现,是一种集中式事件处理机制,允许不同的组件之间进行彼此通信而又不需要相互依赖,达到一种解耦的目的。 …...
LeetCode 热题100 --双指针
双指针 b站UP主蜜糖:由于数据特征的有序性(大小或者正负),所以可以证明当前节点一定是优于过往节点,从而可以通过数据的维度数量的指针,逐步的迭代收敛最终找到最优解。 283.移动零 相关标签 :…...

从《深入设计模式》一书中学到的编程智慧
软件设计原则 优秀设计的特征 在开始学习实际的模式前,让我们来看看软件架构的设计过程,了解一下需要达成目标与需要尽量避免的陷阱。 代码复用 无论是开发何种软件产品,成本和时间都最重要的两个维度。较短的开发时间意味着可比竞争对…...

Redis 基本配置
Redis的配置文件通常位于 /etc/redis/redis.conf。以下是一些常见的Redis配置选项和它们的说明: 基本配置 1. 绑定地址 bind 127.0.0.1默认情况下,Redis只监听本地接口。如果需要远程访问,可以修改成bind 0.0.0.0,不过这会带来…...
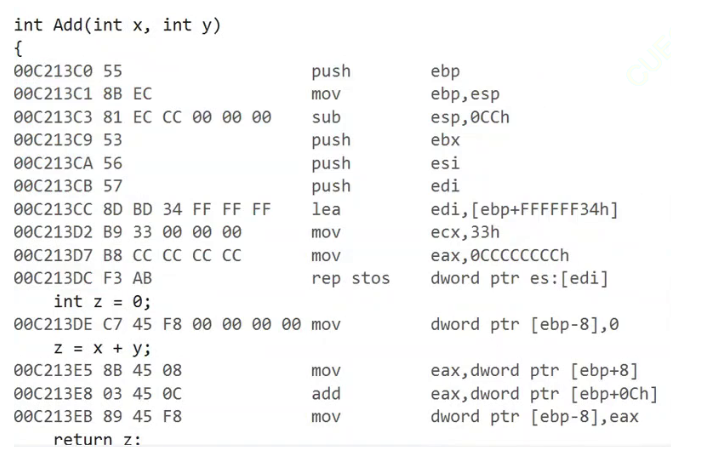
【C++庖丁解牛】函数栈帧的创建与销毁
🍁你好,我是 RO-BERRY 📗 致力于C、C、数据结构、TCP/IP、数据库等等一系列知识 🎄感谢你的陪伴与支持 ,故事既有了开头,就要画上一个完美的句号,让我们一起加油 目录 1. 寄存器2. ebp和esp是如…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

CMake基础:构建流程详解
目录 1.CMake构建过程的基本流程 2.CMake构建的具体步骤 2.1.创建构建目录 2.2.使用 CMake 生成构建文件 2.3.编译和构建 2.4.清理构建文件 2.5.重新配置和构建 3.跨平台构建示例 4.工具链与交叉编译 5.CMake构建后的项目结构解析 5.1.CMake构建后的目录结构 5.2.构…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
