动手学深度学习(Pytorch版)代码实践 -卷积神经网络-27含并行连结的网络GoogLeNet
27含并行连结的网络GoogLeNet


import torch
from torch import nn
from torch.nn import functional as F
import liliPytorch as lp
import matplotlib.pyplot as pltclass Inception(nn.Module):# c1--c4是每条路径的输出通道数def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):super().__init__()# super(Inception, self).__init__(**kwargs)# 线路1,单1x1卷积层self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)# 线路2,1x1卷积层后接3x3卷积层self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)# 线路3,1x1卷积层后接5x5卷积层self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)# 线路4,3x3最大汇聚层后接1x1卷积层self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)def forward(self, x):# 经过每条路径,并应用 ReLU 激活函数p1 = F.relu(self.p1_1(x))p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))p4 = F.relu(self.p4_2(self.p4_1(x)))# 在通道维度上连结输出return torch.cat((p1, p2, p3, p4), dim=1)# 定义模型的各个模块
b1 = nn.Sequential(nn.Conv2d(1, 64, kernel_size=7, stride=2, padding=3), # 第一个卷积层nn.ReLU(), # 激活函数nn.MaxPool2d(kernel_size=3, stride=2, padding=1) # 最大汇聚层
)b2 = nn.Sequential(nn.Conv2d(64, 64, kernel_size=1), # 1x1卷积层nn.ReLU(), # 激活函数nn.Conv2d(64, 192, kernel_size=3, padding=1), # 3x3卷积层nn.ReLU(), # 激活函数nn.MaxPool2d(kernel_size=3, stride=2, padding=1) # 最大汇聚层
)b3 = nn.Sequential(Inception(192, 64, (96, 128), (16, 32), 32), # 第一个Inception块Inception(256, 128, (128, 192), (32, 96), 64), # 第二个Inception块nn.MaxPool2d(kernel_size=3, stride=2, padding=1) # 最大汇聚层
)b4 = nn.Sequential(Inception(480, 192, (96, 208), (16, 48), 64), # 第一个Inception块Inception(512, 160, (112, 224), (24, 64), 64), # 第二个Inception块Inception(512, 128, (128, 256), (24, 64), 64), # 第三个Inception块Inception(512, 112, (144, 288), (32, 64), 64), # 第四个Inception块Inception(528, 256, (160, 320), (32, 128), 128), # 第五个Inception块nn.MaxPool2d(kernel_size=3, stride=2, padding=1) # 最大汇聚层
)b5 = nn.Sequential(Inception(832, 256, (160, 320), (32, 128), 128), # 第一个Inception块Inception(832, 384, (192, 384), (48, 128), 128), # 第二个Inception块nn.AdaptiveAvgPool2d((1, 1)), # 自适应平均汇聚层nn.Flatten() # 展平层
)# 将所有模块串联成一个完整的模型
net = nn.Sequential(b1, # 第一模块b2, # 第二模块b3, # 第三模块b4, # 第四模块b5, # 第五模块nn.Linear(1024, 10) # 最后一层全连接层,输出10个类别
)# 创建一个随机输入张量,并通过每一层,打印输出形状
X = torch.rand(size=(1, 1, 96, 96))
for layer in net:X = layer(X)print(layer.__class__.__name__, 'output shape:\t', X.shape)# 训练参数
lr, num_epochs, batch_size = 0.1, 10, 128
# 加载数据集
train_iter, test_iter = lp.loda_data_fashion_mnist(batch_size, resize=96)
# 训练模型
lp.train_ch6(net, train_iter, test_iter, num_epochs, lr, lp.try_gpu())
# 显示训练过程中的图表
plt.show()# 训练结果:
# 损失 0.254, 训练准确率 0.904, 测试准确率 0.866
# 1534.2 examples/sec on cuda:0# loss 0.246, train acc 0.906, test acc 0.891
# 1492.9 examples/sec on cuda:0
运行效果:

相关文章:

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-27含并行连结的网络GoogLeNet
27含并行连结的网络GoogLeNet import torch from torch import nn from torch.nn import functional as F import liliPytorch as lp import matplotlib.pyplot as pltclass Inception(nn.Module):# c1--c4是每条路径的输出通道数def __init__(self, in_channels, c1, c2, c3, …...
fastadmin多语言切换设置
fastadmin版本:1.4.0.20230711 以简体,繁体,英文为例 一,在application\config.php 里开启多语言 // 是否开启多语言lang_switch_on > true, // 允许的语言列表allow_lang_list > [zh-cn, en,zh-tw], 二…...

如何清理docker build的缓存
在使用 Docker 构建镜像时,Docker 会利用构建缓存来加速后续的构建过程。如果某一层及其所有上层未发生变化,Docker 就会重用这一层的缓存。虽然这可以显著提升构建速度,但有时你可能希望强制 Docker 忽略缓存,以确保从头开始重新…...

OceanBase v4.2 特性解析:如何用分页保序功能解决MySQL模式分页查询不稳定
导言 在MySQL业务迁移OceanBase过程中,经常遇到的一个问题是分页查询结果的不稳定性,这通常需要数据库DBA介入绑定执行计划。下面简单举个例子,以便大家更好地理解为什么有的分页查询,在原来的MySQL数据库下运行没有问题…...
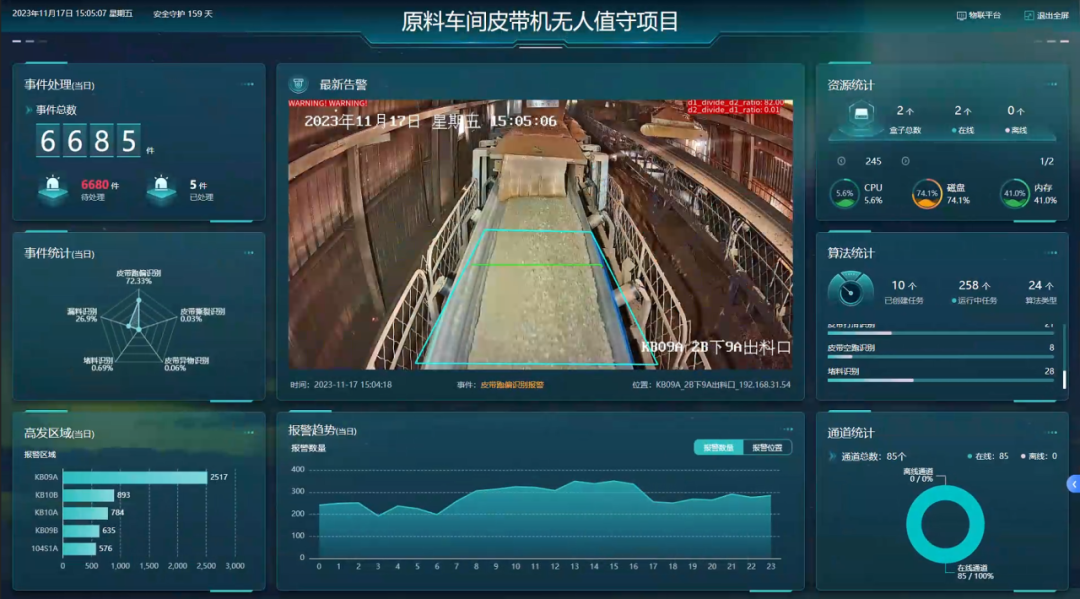
RK3588/算能/Nvidia智能盒子:加速山西铝业智能化转型,保障矿业皮带传输安全稳定运行
近年来,各类矿山事故频发,暴露出传统矿业各环节的诸多问题。随着全国重点产煤省份相继出台相关政策文件,矿业智能化建设进程加快。皮带传输系统升级是矿业智能化的一个重要环节,同时也是降本增效的一个重点方向。 △各省份智能矿山…...

2024.6.24 IDEA中文乱码问题(服务器 控制台 TOMcat)实测已解决
1.问题产生原因: 1.文件编码不一致:如果文件的编码方式与IDEA设置的编码方式不一致,就会产生乱码。确保文件和IDEA使用相同的编码,通常是UTF-8。2.IDEA设置问题:检查IDEA的全局编码设置和项目编码设置是否正确。3.终端…...

桌面编辑器ONLYOFFICE 功能多样性快来试试吧!
目录 ONLYOFFICE 桌面编辑器 8.1 ONLYOFFICE介绍 主要功能和特点 使用场景 1.PDF编辑器 2.幻灯片版式 3.编辑,审阅和查看模式 4.隐藏连接到云版块 5.RTL语言支持和本地化选项 6.媒体播放器 7、其他新功能 8.下载 总结 ONLYOFFICE 桌面编辑器 8.1 官网地…...

三维渲染中的散光圆
三维渲染中的散光圆 散光圆(Circle of Confusion,CoC)是三维渲染和摄影中的一个重要概念,尤其在景深(Depth of Field,DoF)效果的生成中起着关键作用。它描述了在成像过程中,焦点前后…...
Vue3 + Ant-Design 中 a-date-picke 实现选择切换年份 没有鼠标光标,输入框内自带‘年’
效果图: 效果图 <a-date-picker ref"datePicker" v-model:value"year" picker"year" value-format"YYYY年" format"YYYY年" :bordered"false" :allowClear"false" inputReadOnly change&…...
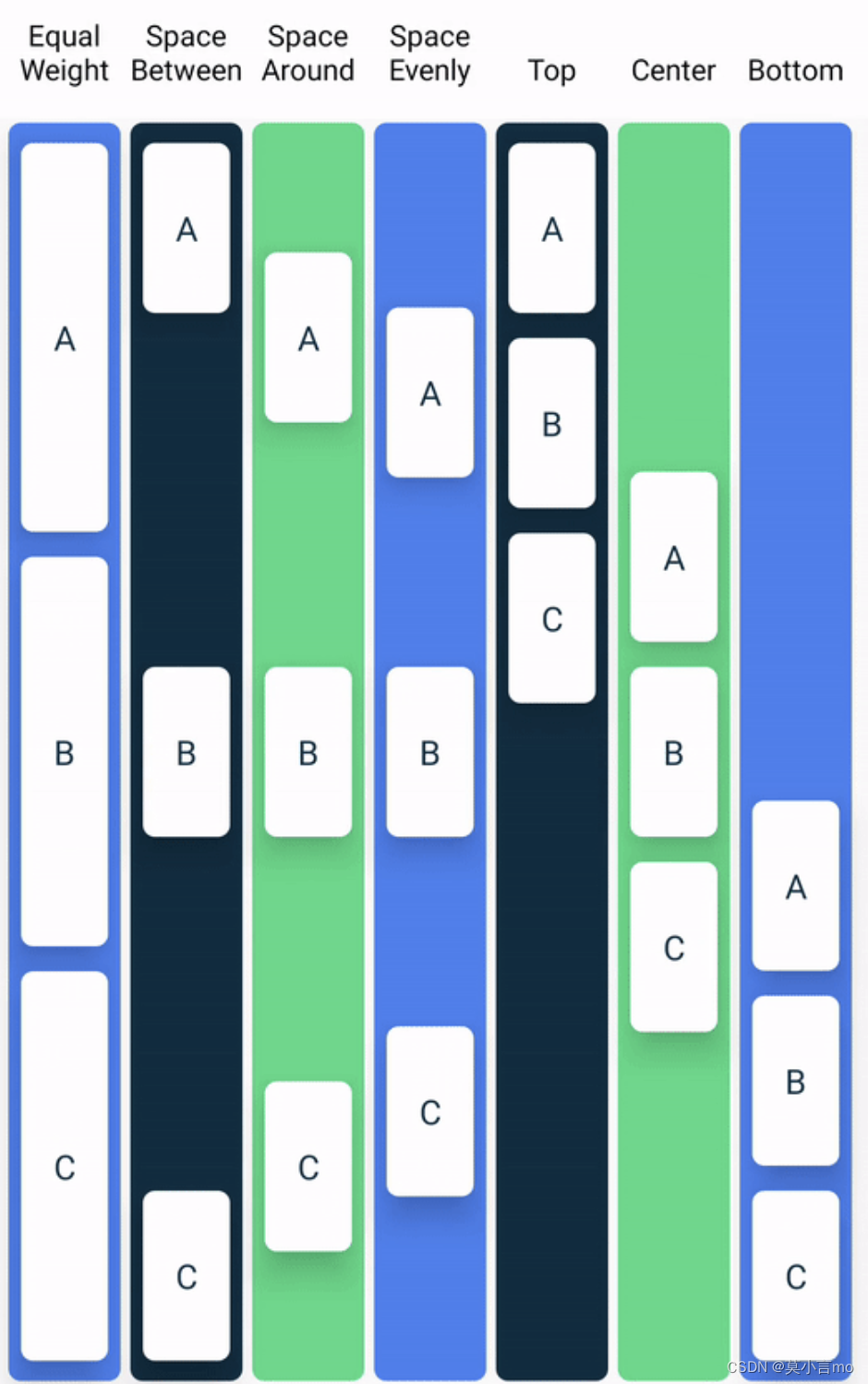
Jetpack Compose_Alignment对其+Arrangement排列
文章目录 1.Alignment 对齐1.1Alignment 对齐方式1.2AbsoluteAlignment 绝对对齐1.3BiasAlignment 偏差对齐1.4BiasAbsoluteAlignment偏差绝对对齐 2.Arrangement 排列2.1Arrangement 排列方式2.2Arrangement.Horizontal2.3Arrangement.Vertical 1.Alignment 对齐 1.1Alignmen…...
)
Vue进阶之Vue无代码可视化项目(五)
Vue无代码可视化项目 编排引擎smooth-dndLeftPanel.vueLayoutView.vuestores/debug.tsstores/editor.tsAppNavigator.vue添加-左侧栏添加到中间部分LayoutView.vuestore/editor.tsLeftPanel.vue移动-中间部分区域的位置更改新建文件夹utils、文件array.tsarray.tsLayoutView.vu…...

【Linux进程】Linux下的---七大进程状态(什么是进程状态?Linux下有哪些进程状态?)
目录 一、前言 二、什么是进程状态? 三、操作系统(OS)下的 --- 进程状态 🔥运行状态🔥 🔥阻塞状态🔥 🔥挂起状态🔥 四、Linux下的7种进程状态 🔥运行状态 -- R🔥…...

Linux的dev/ 和 sys/ 和 proc/ 目录
linux精神: 一切设备皆文件。 设备被抽象成文件 1、 /dev : 该目录放的设备文件,是应用程序和内核的交互文件,应用程序对这些文件的读写控制可以直接访问到实际的设备 应用程序通过mknod创建的文件,如果底层驱动对mknod的设备号…...

代码随想录算法训练营day64 | 98. 所有可达路径
图论理论基础 1、图的种类 整体上一般分为 有向图 和 无向图。 加权有向图,就是图中边是有权值的,加权无向图也是同理。 2、度 无向图中有几条边连接该节点,该节点就有几度 在有向图中,每个节点有出度和入度。出度ÿ…...
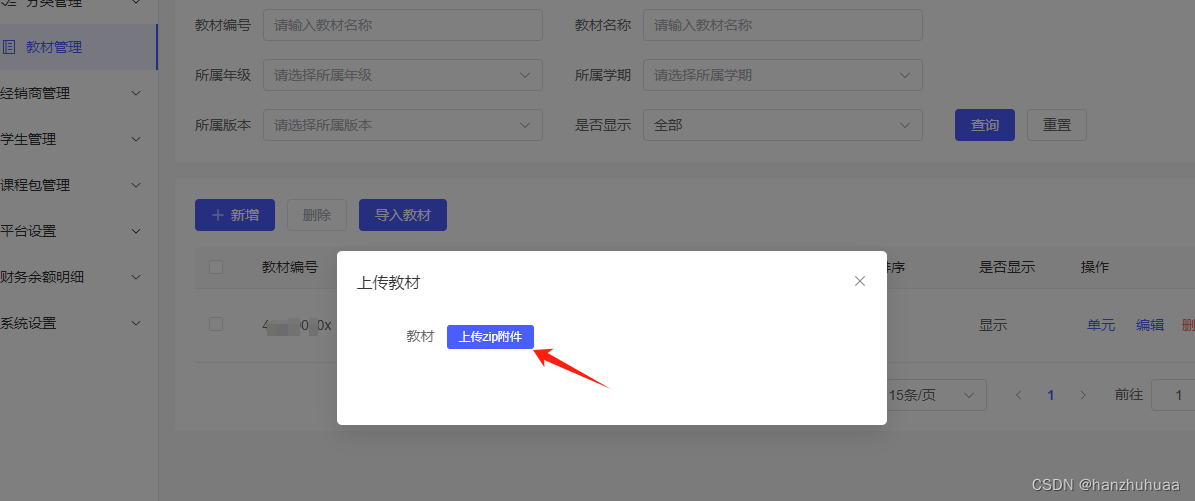
php上传zip压缩包到服务器并解压,解析压缩包内excel表格数据导入到数据库
需求: 1.需要管理后台将excel表格中的每条单词数据导入到数据库中. 2.每条单词数据对应的图片和音频文件需要上传到服务器中. 为了让客户上传数据方便,考虑了一下决定通过后台上传压缩包的方式实现 测试压缩包: 压缩包的目录结构 管理后台导入教材 public function upload…...

48-5 内网渗透 - JuicyPotato、Pipe Potato提权
Juicy Potato Juicy Potato 与 Rotten Potato(烂土豆) 的原理几乎完全相同,只是在后者的基础上做了扩展,以便更灵活地利用 Rotten Potato。Juicy Potato 不再像 Rotten Potato 那样依赖于一个现有的 Meterpreter,并且可以自定义 COM 对象加载的端口,以及根据系统版本更换…...
Windows C++ 应用软件开发从入门到精通详解
目录 1、引言 2、IDE 开发环境介绍 2.1、Visual Studio 2.2、Qt Creator 3、 C语言特性 3.1、熟悉泛型编程 3.2、了解C/C异常处理 3.3、熟练使用STL容器 3.4、熟悉C11新特性 4、Windows 平台的编程技术与调试技能 4.1、需要掌握的若干编程技术和基础知识 4.2、需…...

Leetcode 3195. Find the Minimum Area to Cover All Ones I
Leetcode 3195. Find the Minimum Area to Cover All Ones I 1. 解题思路2. 代码实现 题目链接:3195. Find the Minimum Area to Cover All Ones I 1. 解题思路 这一题还是挺简单的,只要找到所有1所在的元素的上下左右4个边界,作为目标矩形…...

ONLYOFFICE8.1版本桌面编辑器测评
目录 一、引言 二、界面设计:简洁大方,操作便捷 三、功能评测:全面升级,满足多样需求 四、性能评测:稳定流畅,高效运行 五、总结与展望 ONLYOFFICE官网链接:ONLYOFFICE - 企业在线办公应用…...

线性代数|机器学习-P15矩阵A的低秩变换下的逆矩阵
文章目录 1. 单位矩阵的秩1变换1.1 功能说明1.2 证明 2. 单位矩阵 I n I_n In的秩k变换3. 一般矩阵A的秩k变换4. 公式用途4.1 求解方程4.2 卡曼滤波 1. 单位矩阵的秩1变换 1.1 功能说明 假设我们有一个单位矩阵I,列向量u,v那么当我们对单位向量I减去秩为1的矩阵…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

遍历 Map 类型集合的方法汇总
1 方法一 先用方法 keySet() 获取集合中的所有键。再通过 gey(key) 方法用对应键获取值 import java.util.HashMap; import java.util.Set;public class Test {public static void main(String[] args) {HashMap hashMap new HashMap();hashMap.put("语文",99);has…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

【 java 虚拟机知识 第一篇 】
目录 1.内存模型 1.1.JVM内存模型的介绍 1.2.堆和栈的区别 1.3.栈的存储细节 1.4.堆的部分 1.5.程序计数器的作用 1.6.方法区的内容 1.7.字符串池 1.8.引用类型 1.9.内存泄漏与内存溢出 1.10.会出现内存溢出的结构 1.内存模型 1.1.JVM内存模型的介绍 内存模型主要分…...

作为测试我们应该关注redis哪些方面
1、功能测试 数据结构操作:验证字符串、列表、哈希、集合和有序的基本操作是否正确 持久化:测试aof和aof持久化机制,确保数据在开启后正确恢复。 事务:检查事务的原子性和回滚机制。 发布订阅:确保消息正确传递。 2、性…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
