算法设计与分析:动态规划法求扔鸡蛋问题 C++
目录
一、实验目的
二、问题描述
三、实验要求
四、算法思想和实验结果
1、动态规划法原理:
2、解决方法:
2.1 方法一:常规动态规划
2.1.1 算法思想:
2.1.2 时间复杂度分析
2.1.3 时间效率分析
2.2 方法二:动态规划加二分查找最优x
2.2.1 算法思想:
2.2.2 时间复杂度分析
2.2.3 时间效率分析
2.3 方法三:动态规划加逆向求解
2.3.1 算法思想
2.3.2 时间复杂度分析
2.3.3 时间效率分析
3、结果输出示例
一、实验目的
1. 掌握动态规划算法设计思想。
2. 掌握扔鸡蛋问题的动态规划法。
二、问题描述
扔鸡蛋问题是计算机程序设计中的一个经典问题。从一幢楼房的不同楼层往下扔鸡蛋,用最少的最坏情况试验次数,确定鸡蛋不会摔碎的最高安全楼层。仅有一个鸡蛋供试验时,只能采用顺序查找法。有足够多的鸡蛋时,可以采用二分查找法。有多于一个但数量有限的鸡蛋时,采用动态规划方法求解。双蛋问题(two-egg problem)是本问题的一个特例,曾出现于谷歌的程序员面试题中。
有一幢楼房高层。某人准备了N个鸡蛋供试验。他想知道鸡蛋从几层扔下不会摔碎,并确定出最高安全楼层。试验过程中,鸡蛋没有摔碎则可以继续使用,摔碎了则需要换一个鸡蛋继续试验。为保证试验成功,此人要设计一个程序,以最小化最坏情况的试验次数F(M, N)。作为一个数学抽象,本问题采用一些理想化假设:所有鸡蛋抗摔能力相同,不计重复坠地的累积损伤,且忽略试验结果的偶然性。试验成功的标准是在N个鸡蛋用完之前,精确确定最高安全楼层是哪一层。允许有鸡蛋剩余。
如果只有N=1个鸡蛋供试验,则为了保证试验成功,只能从一层开始逐层往上试验。这相当于采用顺序查找算法,最坏试验次数F(M, 1)=M。如果一层就碎了,则最高安全楼层为0。如果M层还不碎,则最高安全楼层为M。
三、实验要求
1. 给出解决问题的动态规划方程;
2. 理论分析该算法的时间复杂度;
3. 分别测试M=10000, 20000, …, 100000, N=20时以及M=50000, N=11, 12, …, 20时的算法运行时间,并分析实验结果;
4. 依次在终端输出M=10000, N=1~20时的F(M, N)值,实验课时检查该代码,限用C或C++语言编写。
四、算法思想和实验结果
1、动态规划法原理:
将复杂问题划分为更小的子问题,通过子问题的最优解来重构原问题的最优解。求解过程中,保存子问题的解,以便在需要时直接查表而不是重复计算,从而减少计算量。
2、解决方法:
2.1 方法一:常规动态规划
2.1.1 算法思想:
用二维数组k[m][n]表示从第m层扔n个鸡蛋的动态规划法最优解,即该实验所要求的最少的最坏情况试验次数。
对于m层、n个鸡蛋的求解,当尝试从第x层扔下一个鸡蛋时,有两种情况:
1)鸡蛋破碎,剩余n-1个鸡蛋,则在第1层至第x-1层(共x-1层)继续尝试,即k[x-1][n-1]。
2)鸡蛋未破碎,仍剩余n个鸡蛋,则在第x+1至m层(共m-x层)继续尝试,即k[m-x][n];
因为题目要求是最坏情况,所以应该取上述两种情况的较大者。又由于要最少实验次数,所以x应该取让前面的较大者尽量小些的值。
得动态规划方程如下:
k[m][n]=1+min{max{k[x-1][n-1],k[m-x][n]}}(x=1,2,3……,m)
实验时
1)对于m=0、m=1或n=1的情况取值依次为0、1、m(在创建**k时就赋值完成)。
2)对于其他值,用三层for循环自底向上依次确定k[i][j]的值。伪代码如下:
F1(m,n)for i=2 to mfor j=2 to nfor x=1 to ik[i][j]=1+max{k[x-1][j-1],k[i-x][j]}return k[m][n]2.1.2 时间复杂度分析
由前面伪代码可知,最外层m-1次,中间层n-1次,最里层i(i=2,3,……,m)次,则时间复杂度为O(n*m^2)。
2.1.3 时间效率分析
由于效率较低,这里降低数据规模,分别测试M=1000, 2000, …, 10000, N=20时以及M=10000,N=11, 12, …, 20时的算法运行时间(对每种情况都运行5次取平均值)。
1)N=20时,以M=1000为基准
| M | 1000 | 2000 | 3000 | 4000 | 5000 | 6000 | 7000 | 8000 | 9000 | 10000 |
| 平均运行时间/ms | 47 | 190 | 434 | 814 | 1310 | 1964 | 2750 | 3706.2 | 4722.4 | 5802 |
| 理论时间/ms | 47 | 188 | 423 | 752 | 1175 | 1692 | 2303 | 3008 | 3807 | 4700 |
得下图:N=20时的实际效率曲线和理论效率曲线图。

两条曲线一开始较贴合,但随着M的增大,实际运行时间与理论运行时间的差(非负)呈现递增趋势。
2)M等于10000时,以N=11为基准:
| N | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 平均运行时间/ms | 2890.5 | 3152.25 | 3443 | 3832 | 4092.5 | 4408 | 4704 | 5180 | 5478 | 5825 |
| 理论时间/ms | 2890.5 | 3153.27 | 3416.05 | 3678.82 | 3941.59 | 4204.36 | 4467.17 | 4729.91 | 4992.68 | 5255.45 |
得下图:M=10000时的实际效率曲线和理论效率曲线图。

与上一个图一样,两条曲线一开始较贴合,但随着N的增大,实际运行时间与理论运行时间的差(非负)呈现递增趋势。
可能原因是
k[i][j]=1+max{k[x-1][j-1],k[i-x][j]}中的数据访问的耗时实际是随着规模的增大而增大的,但分析时间复杂度和理论时间时忽略这个。(实际效率与理论效率之间差某些常数因子)
2.2 方法二:动态规划加二分查找最优x
2.2.1 算法思想:
对于
for x=1 to mk[i][j]=1+max{k[x-1][j-1],k[i-x][j]}当x增大时,k[x-1][j-1]是x相关的非递减函数,而k[i-x][j]是x相关的非递增函数。所以可以在前面的基础上,用二分法求出最优的x,而不是从1到m逐个的尝试、比较。
由于层数为整数,二分到最后有两种情况:
1)二分到最后low!=high,如下图,则应该取点1和点3中次数较小的那个(最坏情况下的最少测试次数),即
k[i][j]=min{k[i-low][j],k[high-1][j-1]}

2)分到最后刚好low=high,如下图:此时x=low=high,k[x-1][j-1=,k[i-x][j]。

伪代码如下:
F2(m,n)for i=2 to mfor j=2 to nl=1;h=i;while l+1<hx=(l+h)/2if k[x-1][j-1]<k[i-x][j]l=xelse if k[x-1][j-1]>k[i-x][j]h=xelse low=high=xk=1+min{k[i-l][j],k[h-1][j-1]}return k[m][n]2.2.2 时间复杂度分析
原来求最优x需m次循环,现在为log m,所以时间复杂度变为O(n*m*log m)
2.2.3 时间效率分析
分别测试M=10000, 20000, …, 100000, N=20时以及M=50000, N=11, 12, …, 20时的算法运行时间(对每种情况都运行20次取平均值)。
1)N=20时,以M=10000为基准
| M | 10000 | 20000 | 30000 | 40000 | 50000 | 60000 | 70000 | 80000 | 90000 | 100000 |
| 平均运行时间/ms | 5 | 9.5 | 14.5 | 19.05 | 29.95 | 34.45 | 41.5 | 47.45 | 57.5 | 62.93 |
| 理论时间/ms | 5 | 10.75 | 16.79 | 23.01 | 29.37 | 35.84 | 42.39 | 49.03 | 55.74 | 62.5 |
得下图:N=20时的实际效率曲线和理论效率曲线图。

两条曲线贴合度较高,说明算法效率基本符合关于m的mlog m级关系。
2)M等于50000时,以N=11为基准
| N | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 平均运行时间/ms | 17 | 18.5 | 19.45 | 20 | 22.5 | 24 | 26.25 | 27.25 | 28.25 | 29 |
| 理论时间/ms | 17 | 18.55 | 20.09 | 21.64 | 23.18 | 24.73 | 26.27 | 27.83 | 29.36 | 30.91 |
得下图:M=50000时的实际效率曲线和理论效率曲线图。

两条曲线较贴合,说明算法效率基本符合关于N的线性关系。
2.3 方法三:动态规划加逆向求解
2.3.1 算法思想
不直接按照在m层、n个鸡蛋的情况下求解最少的最坏情况试验次数,而是逆向求解在n个鸡蛋、r次试验次数且最坏情况下最多能测多少层。找到层数大于m时的最小r。
此时扔鸡蛋,碎了,就继续测楼下;没碎,就继续测楼上。
总的可测楼层数 = 楼上的可测楼层数 + 楼下的可测楼层数 + 1(当前这层楼)。即
k[n][r]=k[n][r-1]+k[n-1][r-1]+1
此时的**k和前面的两种方法的不同,分配的空间不再是k[m+1][n+1],而是为k[n][max],max为一个较大的值(由于实验要求的最大规模M=100000、N=20的解为447,所以这里max取1000,实际未知该解时应取更大些)。
伪代码如下:
F3(m,n)r=0while k[n][r]<m //r不超过mr++for i=1 to nk[i][r]=k[i][r-1]+k[i-1][r-1]+1return r2.3.2 时间复杂度分析
外层while循环(不大于)m次,内层for循环n次,所以时间复杂度为O(n*m)。
2.3.3 时间效率分析
效率较高,m=2000000000,n=20时运行时间仍然小于1ms。
3、结果输出示例
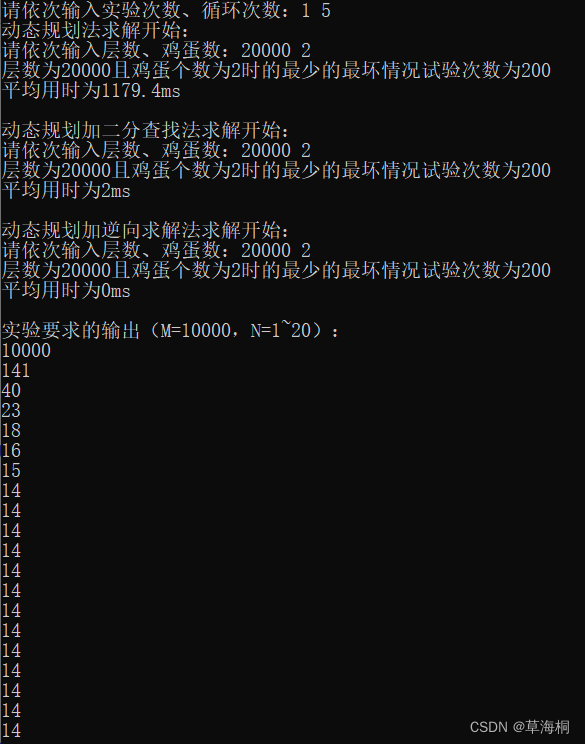
相关文章:

算法设计与分析:动态规划法求扔鸡蛋问题 C++
目录 一、实验目的 二、问题描述 三、实验要求 四、算法思想和实验结果 1、动态规划法原理: 2、解决方法: 2.1 方法一:常规动态规划 2.1.1 算法思想: 2.1.2 时间复杂度分析 2.1.3 时间效率分析 2.2 方法二:动态规划加…...
Java项目:基于SSM框架实现的电子竞技管理平台【ssm+B/S架构+源码+数据库+毕业论文】
一、项目简介 本项目是一套基于SSM框架实现的电子竞技管理平台 包含:项目源码、数据库脚本等,该项目附带全部源码可作为毕设使用。 项目都经过严格调试,eclipse或者idea 确保可以运行! 该系统功能完善、界面美观、操作简单、功能…...

Scala入门介绍
Scala 是一种强大的多范式编程语言,旨在融合面向对象编程和函数式编程的特性。它运行在 Java 虚拟机(JVM)上,因此可以无缝地与 Java 库进行交互。以下是对 Scala 的入门介绍,并附带了一些基本代码示例。 环境设置 首先…...
品牌策划背后的秘密:我为何对此工作情有独钟?
你是否曾有过一个梦想,一份热爱,让你毫不犹豫地投身于一个行业? 我就是这样一个对品牌策划充满热情的人。 从选择职业到现在,我一直在广告行业里“混迹”,一路走来,也见证了许多对品牌策划一知半解的求职…...

超越招聘技术人才目标的最佳技术招聘统计数据
研究发现,难以找到的人才比以往任何时候都更难找到:根据新人才委员会招聘调查报告:2024年难以找到的人才的战略和战略,60%的受访者表示,熟练人才的招聘时间比一年前长。调查进一步揭示了以下关于招聘技术的关键事实&am…...
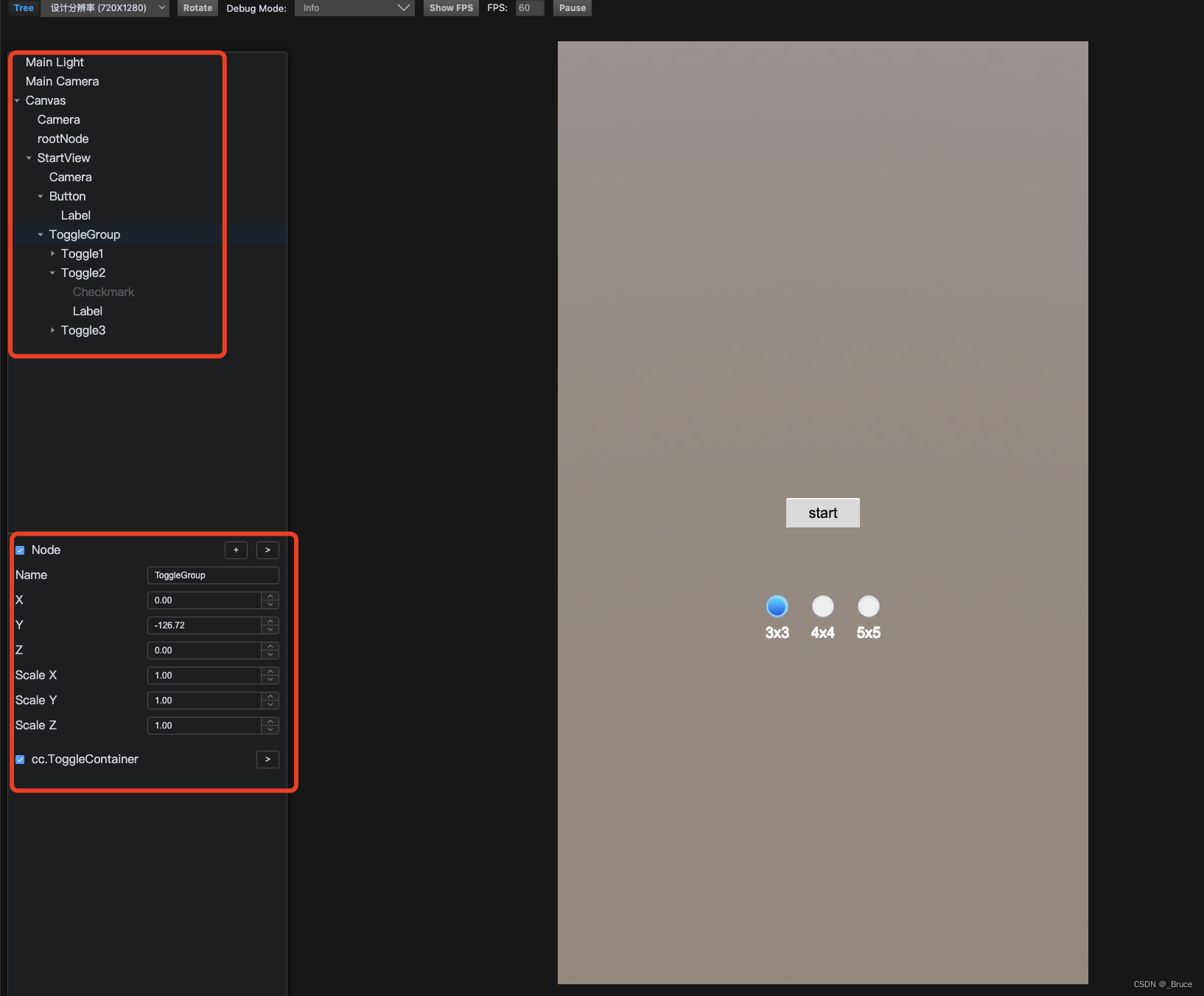
cocos creator 调试插件
适用 Cocos Creator 3.4 版本,cocos creator 使用google浏览器调试时,我们可以把事实运行的节点以节点树的形式显示在浏览器上,支持运行时动态调整位置等、、、 将下载的preview-template插件解压后放在工程根目录下,然后重新运行…...

Clickhouse监控_监控的指标以及Grafana配置Clickhouse指标异常时触发报警
使用PrometheusGrafana来监控Clickhouse服务和性能指标 Clickhouse监控指标的官方文档https://clickhouse.com/docs/zh/operations/monitoring 建议使用PrometheusGrafana组合监控Clickhouse服务和性能指标,数据流向:Prometheus的clickhouse_exporter组件…...

动手学深度学习(Pytorch版)代码实践 -卷积神经网络-27含并行连结的网络GoogLeNet
27含并行连结的网络GoogLeNet import torch from torch import nn from torch.nn import functional as F import liliPytorch as lp import matplotlib.pyplot as pltclass Inception(nn.Module):# c1--c4是每条路径的输出通道数def __init__(self, in_channels, c1, c2, c3, …...
fastadmin多语言切换设置
fastadmin版本:1.4.0.20230711 以简体,繁体,英文为例 一,在application\config.php 里开启多语言 // 是否开启多语言lang_switch_on > true, // 允许的语言列表allow_lang_list > [zh-cn, en,zh-tw], 二…...

如何清理docker build的缓存
在使用 Docker 构建镜像时,Docker 会利用构建缓存来加速后续的构建过程。如果某一层及其所有上层未发生变化,Docker 就会重用这一层的缓存。虽然这可以显著提升构建速度,但有时你可能希望强制 Docker 忽略缓存,以确保从头开始重新…...

OceanBase v4.2 特性解析:如何用分页保序功能解决MySQL模式分页查询不稳定
导言 在MySQL业务迁移OceanBase过程中,经常遇到的一个问题是分页查询结果的不稳定性,这通常需要数据库DBA介入绑定执行计划。下面简单举个例子,以便大家更好地理解为什么有的分页查询,在原来的MySQL数据库下运行没有问题…...
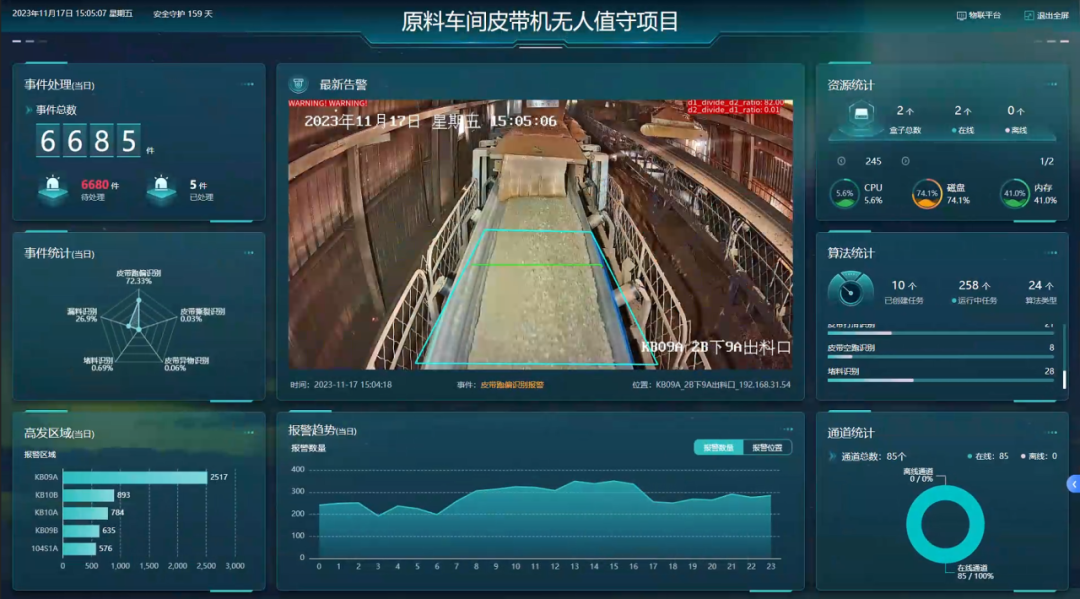
RK3588/算能/Nvidia智能盒子:加速山西铝业智能化转型,保障矿业皮带传输安全稳定运行
近年来,各类矿山事故频发,暴露出传统矿业各环节的诸多问题。随着全国重点产煤省份相继出台相关政策文件,矿业智能化建设进程加快。皮带传输系统升级是矿业智能化的一个重要环节,同时也是降本增效的一个重点方向。 △各省份智能矿山…...

2024.6.24 IDEA中文乱码问题(服务器 控制台 TOMcat)实测已解决
1.问题产生原因: 1.文件编码不一致:如果文件的编码方式与IDEA设置的编码方式不一致,就会产生乱码。确保文件和IDEA使用相同的编码,通常是UTF-8。2.IDEA设置问题:检查IDEA的全局编码设置和项目编码设置是否正确。3.终端…...

桌面编辑器ONLYOFFICE 功能多样性快来试试吧!
目录 ONLYOFFICE 桌面编辑器 8.1 ONLYOFFICE介绍 主要功能和特点 使用场景 1.PDF编辑器 2.幻灯片版式 3.编辑,审阅和查看模式 4.隐藏连接到云版块 5.RTL语言支持和本地化选项 6.媒体播放器 7、其他新功能 8.下载 总结 ONLYOFFICE 桌面编辑器 8.1 官网地…...

三维渲染中的散光圆
三维渲染中的散光圆 散光圆(Circle of Confusion,CoC)是三维渲染和摄影中的一个重要概念,尤其在景深(Depth of Field,DoF)效果的生成中起着关键作用。它描述了在成像过程中,焦点前后…...
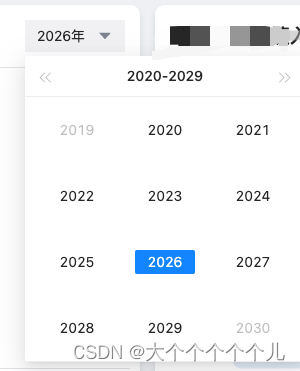
Vue3 + Ant-Design 中 a-date-picke 实现选择切换年份 没有鼠标光标,输入框内自带‘年’
效果图: 效果图 <a-date-picker ref"datePicker" v-model:value"year" picker"year" value-format"YYYY年" format"YYYY年" :bordered"false" :allowClear"false" inputReadOnly change&…...
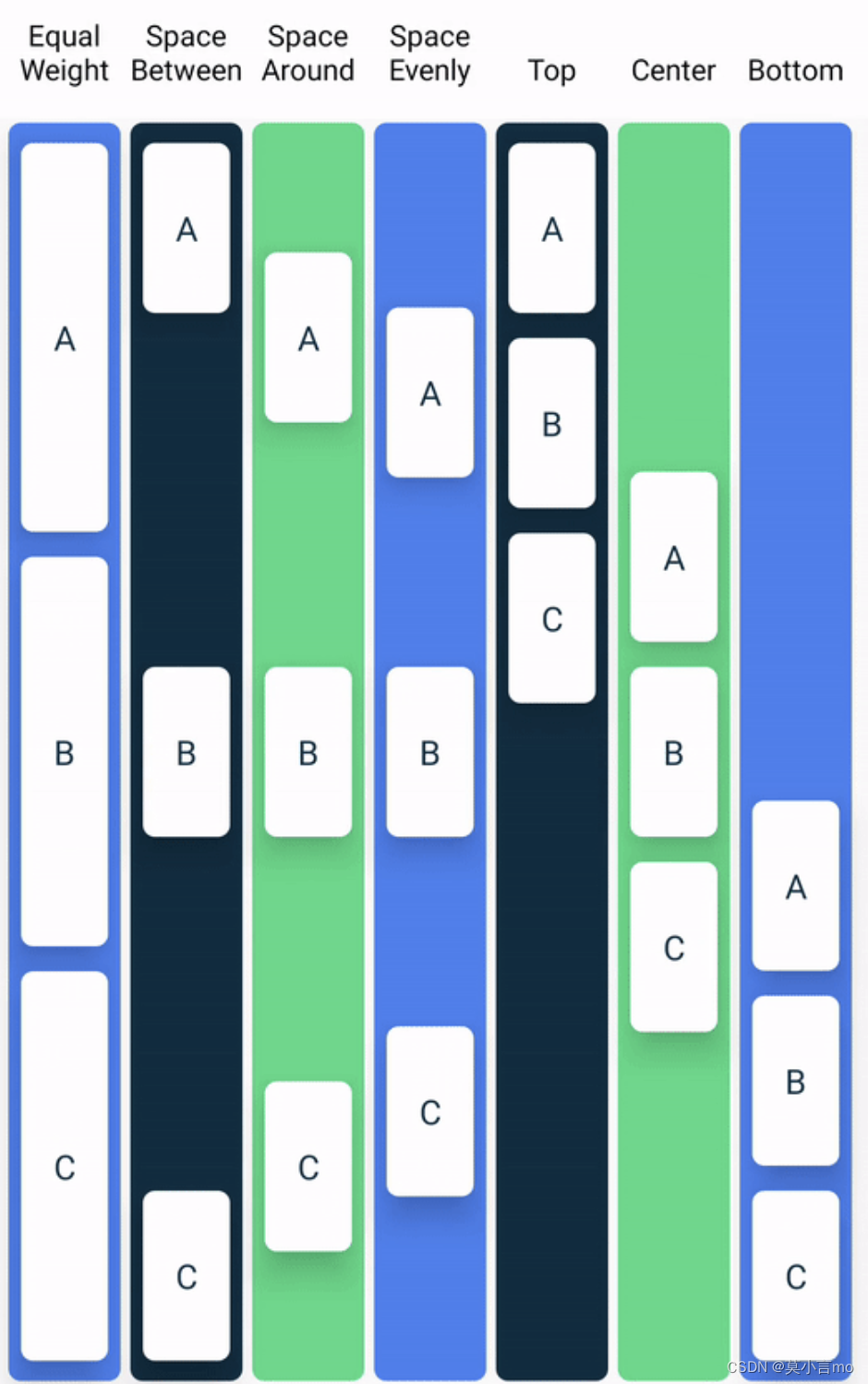
Jetpack Compose_Alignment对其+Arrangement排列
文章目录 1.Alignment 对齐1.1Alignment 对齐方式1.2AbsoluteAlignment 绝对对齐1.3BiasAlignment 偏差对齐1.4BiasAbsoluteAlignment偏差绝对对齐 2.Arrangement 排列2.1Arrangement 排列方式2.2Arrangement.Horizontal2.3Arrangement.Vertical 1.Alignment 对齐 1.1Alignmen…...
)
Vue进阶之Vue无代码可视化项目(五)
Vue无代码可视化项目 编排引擎smooth-dndLeftPanel.vueLayoutView.vuestores/debug.tsstores/editor.tsAppNavigator.vue添加-左侧栏添加到中间部分LayoutView.vuestore/editor.tsLeftPanel.vue移动-中间部分区域的位置更改新建文件夹utils、文件array.tsarray.tsLayoutView.vu…...

【Linux进程】Linux下的---七大进程状态(什么是进程状态?Linux下有哪些进程状态?)
目录 一、前言 二、什么是进程状态? 三、操作系统(OS)下的 --- 进程状态 🔥运行状态🔥 🔥阻塞状态🔥 🔥挂起状态🔥 四、Linux下的7种进程状态 🔥运行状态 -- R🔥…...

Linux的dev/ 和 sys/ 和 proc/ 目录
linux精神: 一切设备皆文件。 设备被抽象成文件 1、 /dev : 该目录放的设备文件,是应用程序和内核的交互文件,应用程序对这些文件的读写控制可以直接访问到实际的设备 应用程序通过mknod创建的文件,如果底层驱动对mknod的设备号…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

Python Einops库:深度学习中的张量操作革命
Einops(爱因斯坦操作库)就像给张量操作戴上了一副"语义眼镜"——让你用人类能理解的方式告诉计算机如何操作多维数组。这个基于爱因斯坦求和约定的库,用类似自然语言的表达式替代了晦涩的API调用,彻底改变了深度学习工程…...
