「动态规划」如何求最长递增子序列的长度?
300. 最长递增子序列![]() https://leetcode.cn/problems/longest-increasing-subsequence/description/
https://leetcode.cn/problems/longest-increasing-subsequence/description/
给你一个整数数组nums,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其余元素的顺序。例如,[3,6,2,7]是数组[0,3,1,6,2,2,7]的子序列。
- 输入:nums = [10,9,2,5,3,7,101,18],输出:4,解释:最长递增子序列是[2,3,7,101],因此长度为4。
- 输入:nums = [0,1,0,3,2,3],输出:4。
- 输入:nums = [7,7,7,7,7,7,7],输出:1。
提示:1 <= nums.length <= 2500,-10^4 <= nums[i] <= 10^4。
进阶:你能将算法的时间复杂度降低到O(nlog(n))吗?
我们用动态规划的思想来解决这个问题。
确定状态表示:根据经验和题目要求,我们用dp[i]表示:以i位置为结尾的所有子序列中,最长递增子序列的长度。
推导状态转移方程:以i位置为结尾的所有子序列分为2类:长度为1的子序列,长度大于1的子序列。如果子序列的长度是1,那么这个子序列是递增子序列。下面我们考虑长度大于1的子序列。
如果以i位置为结尾的子序列的长度大于1,我们可以继续细分为:i位置元素的前面是i - 1位置元素的子序列,i位置元素的前面是i - 2位置元素的子序列,i位置元素的前面是i - 3位置元素的子序列,……,i位置元素的前面是0位置元素的子序列。也就是说,如果子序列中,i位置元素的前面是j位置元素,那么j的范围是[0, i - 1]。
对于每一个j,如果nums[j] < nums[i],那么这个子序列就有可能是递增子序列。要想这个子序列尽可能得长,就要找到以j位置为结尾的最长递增子序列,在这个子序列后面添加nums[i],即为以i位置为结尾的最长递增子序列。
综上所述,dp[i]应该取:「1」和「所有满足0 <= j < i并且nums[j] < nums[i]的j中,最大的dp[j]加1」的较大值。
所以,我们可以把dp表的值都初始化为1,其中dp[0] = 1是显然的。如果i > 0,那么dp[i]就应该取:所有满足0 <= j < i并且nums[j] < nums[i]的j中,最大的dp[j]加1。
填表顺序:根据状态转移方程,显然应从左往右填表。
返回值:根据状态表示,应返回dp表的最大值。
细节问题:dp表的规模和nums相同,均为1 x n。
class Solution {
public:int lengthOfLIS(vector<int>& nums) {int n = nums.size();// 创建dp表vector<int> dp(n, 1);// 填表for (int i = 1; i < n; i++) {for (int j = 0; j < i; j++) {if (nums[j] < nums[i]) {dp[i] = max(dp[i], dp[j] + 1);}}}return *max_element(dp.begin(), dp.end());}
};相关文章:
「动态规划」如何求最长递增子序列的长度?
300. 最长递增子序列https://leetcode.cn/problems/longest-increasing-subsequence/description/ 给你一个整数数组nums,找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列,删除(或不删除)数组中的元素而不改变其…...

深度神经网络DNN概念科普
深度神经网络DNN概念科普 深度神经网络(Deep Neural Network, DNN)是机器学习领域中一类具有多层结构的神经网络模型,它能够通过学习数据中的复杂模式来解决非线性问题。下面是对深度神经网络的详细解析: 基本组成部分 输入层&…...
Tomcat WEB站点部署
目录 1、使用war包部署web站点 2、自定义默认网站目录 3、部署开源站点(jspgou商城) 对主机192.168.226.22操作 对主机192.168.226.20操作 上线的代码有两种方式: 第一种方式是直接将程序目录放在webapps目录下面,这种方式…...

IPv6 中 MAC 33:33 的由来
一、33:33 由来 1. RFC9542 - 2024-05-02 Note IANA allocates addresses under the IANA OUI (00-00-5E) as explained in [RFC9542]. Unicast addresses under the IANA OUI start with 00-00-5E, while multicast addresses under the IANA OUI start with 01-00-5E. In t…...
告别手动邮件处理:使用imbox库轻松管理你的收件箱
imbox库简介: imbox是一个强大的Python库,专为与IMAP服务器交互而设计.IMAP(Internet Message Access Protocol)是一种用于电子邮件的标准协议,允许用户在远程服务器上管理邮件.imbox库通过IMAP协议与邮件服务器通信,帮助用户轻松地读取、搜索…...
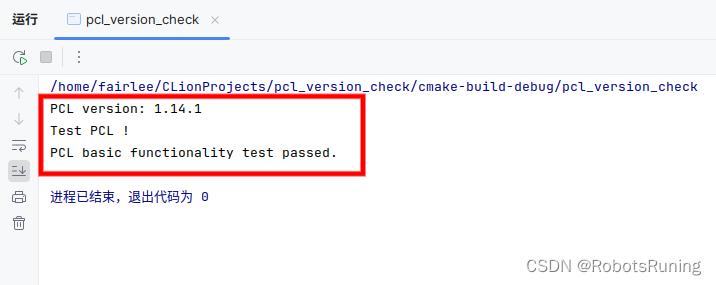
Ubuntu 18.04 安装 PCL 1.14.1
在进行科研项目时,我们常常需要将 C 和 Python 结合起来编程。然而,每次将 PCL(Point Cloud Library)的内容添加到 CMakeLists.txt 文件中时都会报错。在深入分析后,我们推测可能是当前使用的 PCL 1.8 版本与现有程序不…...
公司logo设计大全怎么找?直接帮你设计logo
公司logo设计大全怎么找?在品牌塑造的过程中,Logo无疑是至关重要的一环。一个优秀的Logo不仅能够有效传达公司的核心理念和品牌形象,还能在消费者心中留下深刻的印象。然而,对于许多初创公司或小型企业来说,制作出适合…...

如何调整C#中数组的大小
前言 数组存储多个相同类型的一种非常常用的数据结构。它长度是固定,也就是数组一旦创建大小就固定了。C# 数组不支持动态长度。那在C#中是否有方法可以调整数组大小呢?本文将通过示例介绍一种调整一维数组大小的方法。 方法 数组实例是从 System.Arr…...
通过言语和非言语检索线索描绘睡眠中的记忆再激活茗创科技茗创科技
摘要 睡眠通过重新激活新形成的记忆痕迹来巩固记忆。研究睡眠中记忆再激活的一种方法是让睡眠中的大脑再次暴露于听觉检索线索(定向记忆再激活范式)。然而,记忆线索的声学特性在多大程度上影响定向记忆再激活的有效性,目前还没有得到充分探索。本研究通…...

MDPI旗下SSCI最新影响因子目录出炉!“水刊“Sustainability表现如何?
本周投稿推荐 SSCI • 1区,4.0-5.0(无需返修,提交可录) EI • 各领域沾边均可(2天录用) CNKI • 7天录用-检索(急录友好) SCI&EI • 4区生物医学类,0.1-0.5&…...

Matlab基础篇:数据输入输出
前言 数据输入和输出是 Matlab 数据分析和处理的核心部分。良好的数据输入输出能够提高工作效率,并确保数据处理的准确性。本文将详细介绍 Matlab 数据输入输出的各种方法,包括导入和导出数据、数据处理和数据可视化。 一、导入数据 Matlab 提供了多种方…...
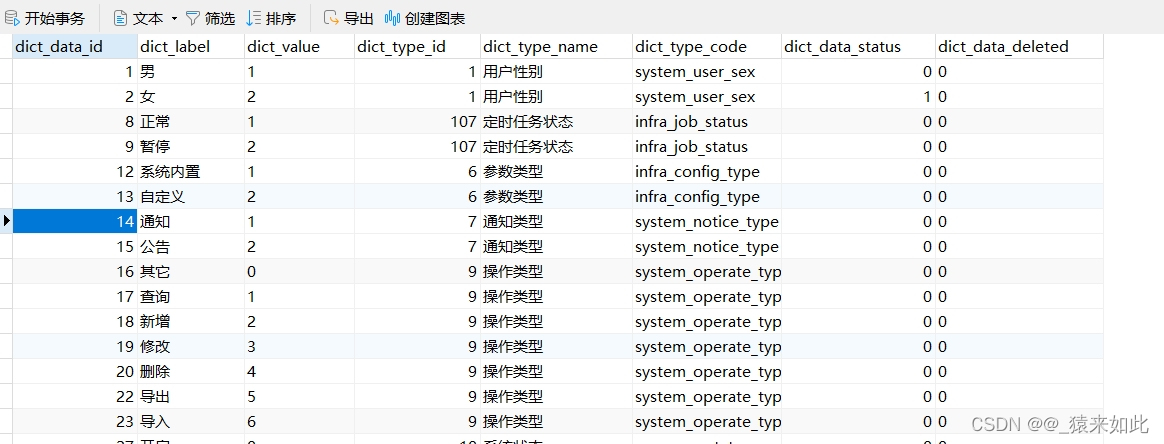
MySQL字典数据库设计与实现 ---项目实战
软件准备✍:Mysql与Navicat可视化命令大全 ----项目实战 文章前言部分 目录 一.摘要 二.设计内容 三.项目实现 一.摘要 本项目关注于字典数据库表结构的设计和数据管理。通过现有的sql文件,实现system_dict_type和system_dict_data两个数据表。随后…...

python数据分析——数据预处理
数据预处理 前言一、查看数据数据表的基本信息查看info()示例 查看数据表的大小shape()示例 数据格式的查看type()dtype()dtypes()示例一示例二 查看具体的数据分布describe()示例 二…...
【Python】使用matplotlib绘制图形(曲线图、条形图、饼图等)
文章目录 一、什么是matplotlib二、matplotlib 支持的图形三、如何使用matplotlib1. 安装matplotlib2. 导入matplotlib.pyplot3. 准备数据4. 绘制图形5. 定制图形6. 显示或保存图形7. (可选)使用subplots创建多个子图注意事项: 四、常见图形使…...

vue下载本地xls模版静态文件
需求导入的下载模版不想放在服务器放在前端本地下载静态资源最简单的方式直接访问 public 文件夹下的文件 方法一:使用静态文件路径 将文件放在 public 文件夹中: 把你的文件从 src/assets 移动到 public 文件夹。例如:public/template.xls。…...

手机开热点,里面的WPA2-Personal和WPA3-Personal的区别
WPA2-Personal和WPA3-Personal这两种协议都是用来保护无线网络安全的,但它们在加密强度和安全性方面有所不同。 WPA2-Personal (Wi-Fi Protected Access 2) WPA2是目前最广泛使用的Wi-Fi安全标准之一。它使用AES(Advanced Encryption Standard…...

算法课程笔记——点积叉积
算法课程笔记——点积叉积...
详解 | DigiCert EV代码签名证书
简介 DigiCert EV 代码签名证书是一种高级别的代码签名证书,它不仅提供了标准代码签名证书的所有安全特性,还增加了额外的身份验证流程,以确保软件开发者或发布者的身份得到最严格验证。这对于提升软件的信任度、防止恶意篡改和确保下载安全…...
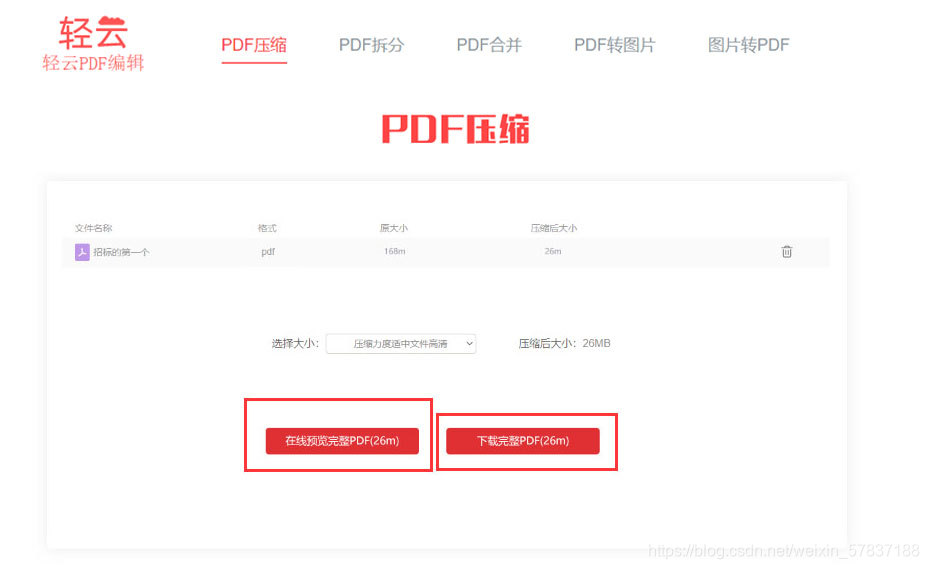
pdf压缩大小,PDF压缩大小不影响清晰度
你是否曾为PDF文件过大而烦恼?想要分享或上传文件时,却因为它的体积而束手无策?别担心,今天我将为大家分享一些简单实用的 PDF 压缩技巧,让你的文件轻松压缩pdf。 打开“轻云处理pdf官网”, 的网站。然后上…...
项目管理必备工具:2024年十大软件排行榜
有效的工具不仅可以帮助团队保持组织性,还能显著提高项目完成率。选择合适的项目管理软件,对于实现这些目标至关重要。 在2024年的各大权威榜单中,排名前十的项目管理软件包括:PingCode、Worktile(国内)&am…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
)
安卓基础(aar)
重新设置java21的环境,临时设置 $env:JAVA_HOME "D:\Android Studio\jbr" 查看当前环境变量 JAVA_HOME 的值 echo $env:JAVA_HOME 构建ARR文件 ./gradlew :private-lib:assembleRelease 目录是这样的: MyApp/ ├── app/ …...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Spring Boot + MyBatis 集成支付宝支付流程
Spring Boot MyBatis 集成支付宝支付流程 核心流程 商户系统生成订单调用支付宝创建预支付订单用户跳转支付宝完成支付支付宝异步通知支付结果商户处理支付结果更新订单状态支付宝同步跳转回商户页面 代码实现示例(电脑网站支付) 1. 添加依赖 <!…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...
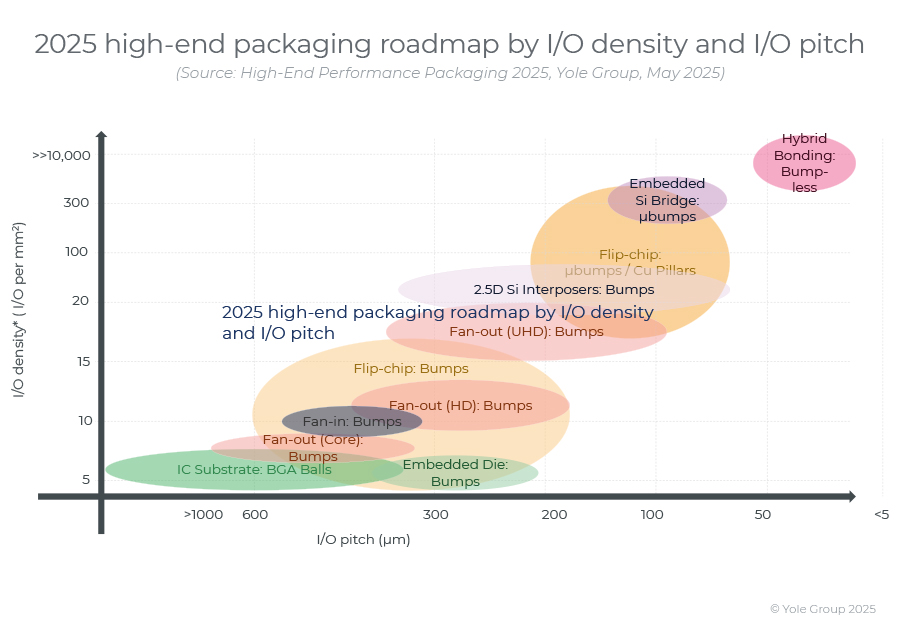
高端性能封装正在突破性能壁垒,其芯片集成技术助力人工智能革命。
2024 年,高端封装市场规模为 80 亿美元,预计到 2030 年将超过 280 亿美元,2024-2030 年复合年增长率为 23%。 细分到各个终端市场,最大的高端性能封装市场是“电信和基础设施”,2024 年该市场创造了超过 67% 的收入。…...
