最小生成树模板(prim,heap-prim,kruskal)
prim
出圈法,时间复杂度 O ( n 2 ) O(n^2) O(n2)
#include<iostream>
#include<vector>
using namespace std;
#define MAX_N 5000
#define inf 100000000
struct edge{int v,w;
};
vector<edge>e[MAX_N+5];
int d[MAX_N+5],vis[MAX_N+5];
int n,m;
int ans=0,cnt=0;
bool prim(int s)
{for(int i=0;i<=n;i++)d[i]=inf;d[s]=0;for(int i=1;i<=n;i++){int u=0;for(int j=1;j<=n;j++)if(!vis[j]&&d[j]<d[u])u=j;vis[u]=1;ans+=d[u];if(d[u]!=inf)cnt++;for(auto ed:e[u]){int v=ed.v,w=ed.w;if(d[v]>w)d[v]=w;}}return n==cnt;
}
int main()
{cin>>n>>m;for(int i=1,a,b,c;i<=m;i++){scanf("%d%d%d",&a,&b,&c);e[a].push_back({b,c});e[b].push_back({a,c});}if(!prim(1)){cout<<"orz"<<endl;return 0;}else{cout<<ans<<endl;return 0;}return 0;}
heap-prim
出队法,时间复杂度 O ( m l o g m ) O(mlogm) O(mlogm)
#include<iostream>
#include<vector>
#include<queue>
using namespace std;
#define MAX_N 5000
#define inf 100000000
struct edge{int v,w;
};
vector<edge>e[MAX_N+5];
int d[MAX_N+5],vis[MAX_N+5];
int n,m;
int ans=0,cnt=0;
priority_queue<pair<int,int>>q;
bool prim(int s)
{for(int i=0;i<=n;i++)d[i]=inf;d[s]=0;q.push({0,s});while(!q.empty()){int u=q.top().second;q.pop();if(vis[u])continue;vis[u]=1;ans+=d[u];cnt++;for(auto ed:e[u]){int v=ed.v,w=ed.w;if(d[v]>w){d[v]=w;q.push({-d[v],v});}}}return n==cnt;
}
int main()
{cin>>n>>m;for(int i=1,a,b,c;i<=m;i++){scanf("%d%d%d",&a,&b,&c);e[a].push_back({b,c});e[b].push_back({a,c});}if(!prim(1)){cout<<"orz"<<endl;return 0;}else{cout<<ans<<endl;return 0;}return 0;}
kruskal
加边法,时间复杂度 O ( m l o g m ) O(mlogm) O(mlogm)
#include<iostream>
#include<algorithm>
using namespace std;
#define MAX_N 5000
#define MAX_M 200000
#define inf 100000000
struct edge{int u,v,w;bool operator<(const edge&t){return w<t.w;}
}e[MAX_M+5];
int k=0;
int n,m;
int fa[MAX_N+5],ans,cnt;
int find(int x)
{return fa[x]==x?x:find(fa[x]);
}
bool kruskal(){sort(e+1,e+m+1);for(int i=1;i<=n;i++)fa[i]=i;for(int i=1;i<=m;i++){int x=find(e[i].u);int y=find(e[i].v);if(x!=y){fa[x]=y;ans+=e[i].w;cnt++;}}return cnt==n-1;
}
int main()
{cin>>n>>m;for(int i=1,a,b,c;i<=m;i++){scanf("%d%d%d",&a,&b,&c);e[++k]={a,b,c};}if(!kruskal()){cout<<"orz"<<endl;return 0;}else{cout<<ans<<endl;return 0;}return 0;}
相关文章:
)
最小生成树模板(prim,heap-prim,kruskal)
prim 出圈法,时间复杂度 O ( n 2 ) O(n^2) O(n2) #include<iostream> #include<vector> using namespace std; #define MAX_N 5000 #define inf 100000000 struct edge{int v,w; }; vector<edge>e[MAX_N5]; int d[MAX_N5],vis[MAX_N5]; int n,m…...

Centos 7 或 8配置国内yum源及epel源-1
官方教程 Yum工具详解 清理Yum缓存:[rootqfedu.com ~]# yum clean all缓存软件包信息: 提高搜索/安装软件的速度[rootqfedu.com ~]# yum makecache查询yum源信息: [rootqfedu.com ~]# yum repolist 查找软件:[rootqfedu.com ~]# yum search mysql 此命令会搜索到系…...

轻松解决Android复杂数据结构序列化
问题描述 当我编写quickupload库时,因为需要在 Service中进行上传任务,向Service传递时我发现需要传递的数据很多并且结构复杂,如果处理不好就会导致以下几个问题 耗时: 需要更多时间进行开发和测试以确保正确的数据处理。容易出错: 由于手…...

解析PDF文件中的图片为文本
解析PDF文件中的图片为文本 1 介绍 解析PDF文件中的图片,由两种思路,一种是自己读取PDF文件中的图片,然后用OCR解析,例如:使用PyMuPDF读取pdf文件,再用PaddleOCR或者Tesseract-OCR识别文字。另一种使用第…...

微信小程序表单
在我们的课程中,我们深入探讨了微信小程序表单的开发和应用。以下是我们课程的主要内容和收获: 一、课程目标 本课程旨在帮助学生掌握微信小程序表单的基本概念、开发流程和最佳实践。学生将学习如何创建和配置表单组件,处理表单数据…...
--学习记录)
Javascript高级程序设计(第四版)--学习记录
var关键字:定义变量同时可以进行赋值 var message"hello" message 10 可以改变保存的值,也可以改变值的类型,但是不推荐这样写。 var声明的变量会成为包含它的函数的局部变量。 function test(){ var message "hello";…...

DVWA-CSRF-samesite分析
拿DVWA的CSRF为例子 接DVWA的分析,发现其实Impossible的PHPSESSID是设置的samesite1. 参数的意思参考Set-Cookie SameSite:控制 cookie 是否随跨站请求一起发送,这样可以在一定程度上防范跨站请求伪造攻击(CSRF)。 下面用DVWA CS…...

代码随想录训练营Day48
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、买卖股票的最佳时机4二、买卖股票的最佳时机含冷冻期三、买卖股票含手续费 前言 提示:这里可以添加本文要记录的大概内容: 今天是…...
:导航守卫_renderroutes)
React进阶(五):导航守卫_renderroutes
在《React进阶(四):路由介绍》博文中,介绍了React路由相关知识,在实际项目开发过程中,路由之间的跳转必定涉及权限、用户是否登陆等限定条件的判定,故需要导航守卫来完成这一事项。 在实现reac…...

Python基础系列教程:从零开始学习Python
Python有很多功能强大的机器学习和大数据分析包,适合对大数据和人工智能感兴趣的同学学习。要想了解一门语言,首先需要了解它的语法。本文将介绍Python的一些基础语法,包括数据类型、变量类型、条件控制、循环结构等内容。废话少说࿰…...

deepl翻译的PDF文档保护密码解除
1、首先将后缀名(.docx)修改为压缩包格式(.zip)。 2、修改解密word加密.py里zip的位置,和新生成的zip的位置和名称 import zipfile import xml.etree.ElementTree as ET import os import shutil# 定义文件路径 zip_file_path rC:\Users\Administrator\Desktop\新…...

LeetCode 算法:二叉树的直径 c++
原题链接🔗:二叉树的直径 难度:简单⭐️ 题目 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由…...
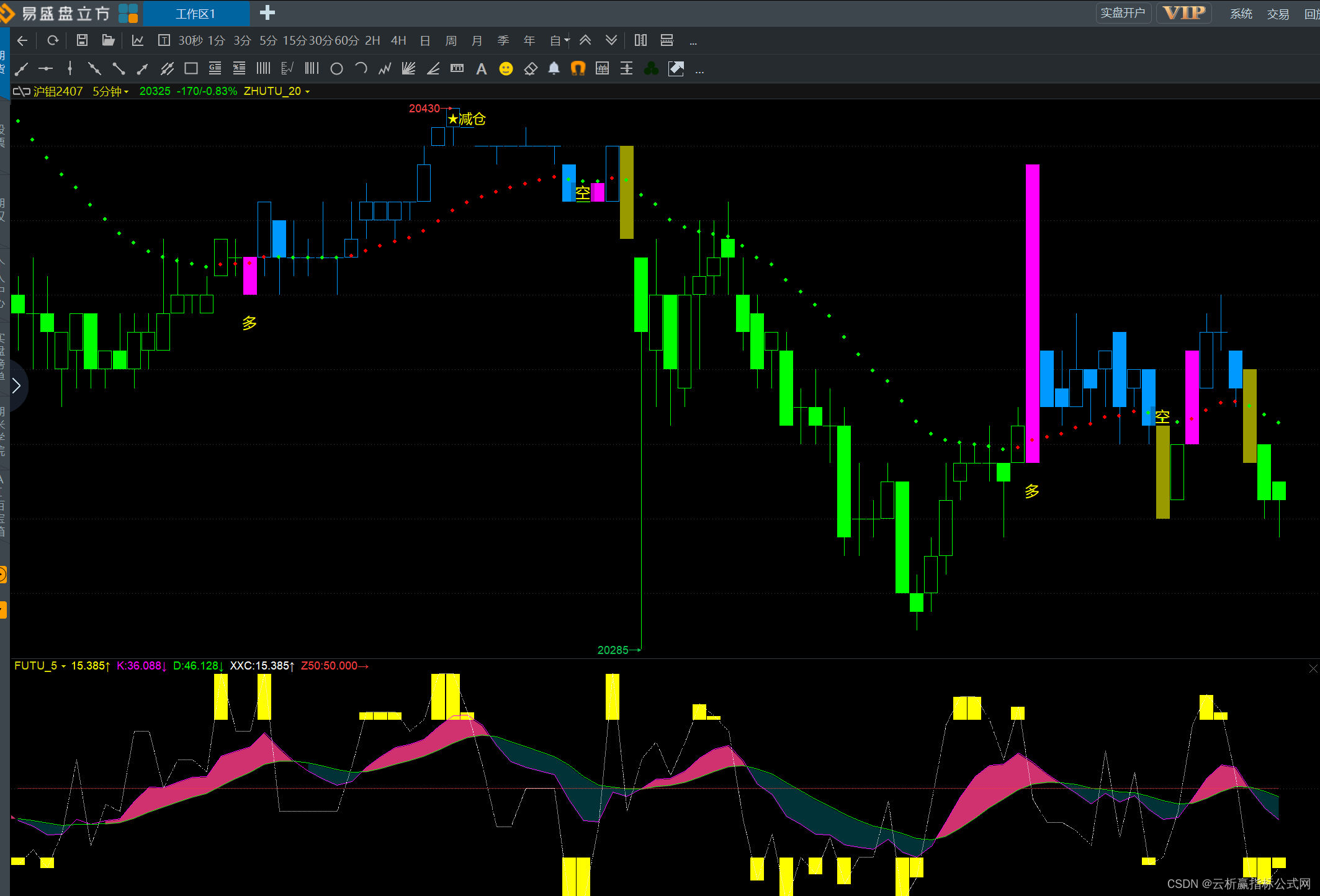
盘立方期货Kdj幅图指标公式源码
盘立方期货Kdj幅图指标公式源码: N:250; WR1:100-100*(HHV(HIGH,N)-CLOSE)/(HHV(HIGH,N)-LLV(LOW,N)),DOT,COLORLIGHTGREEN; EW:EMA(WR1,5); STICKLINE(WR1<20,WR1,20,1,0),COLORYELLOW; STICKLINE(WR1>80,WR1,80,1,0),COLORYELLOW; RSV:(CLOSE-LLV(LOW…...
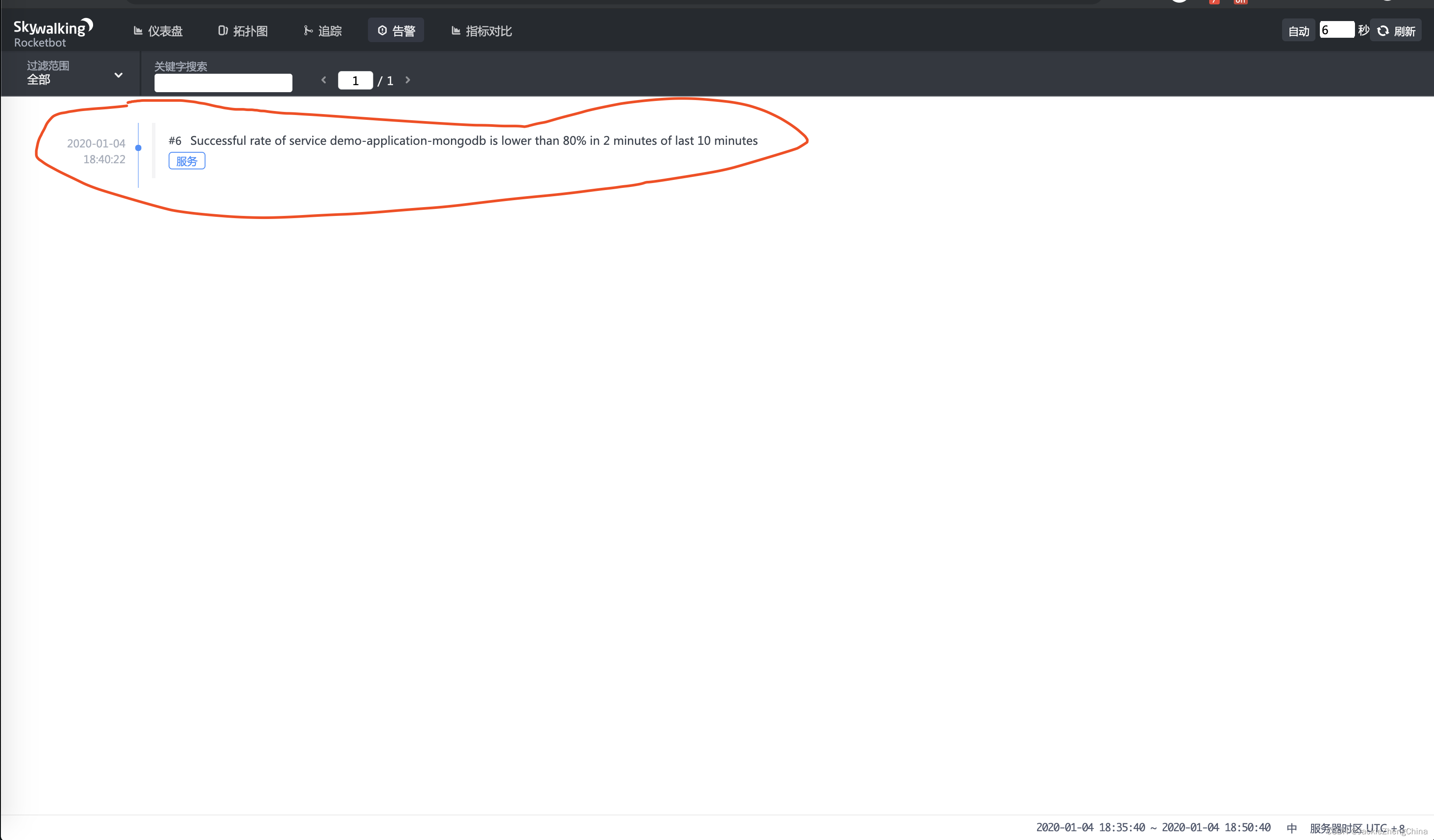
SkyWalking 极简入门
1. 概述 1.1 概念 SkyWalking 是什么? FROM Apache SkyWalking 分布式系统的应用程序性能监视工具,专为微服务、云原生架构和基于容器(Docker、K8s、Mesos)架构而设计。 提供分布式追踪、服务网格遥测分析、度量聚合和可视化一体…...
)
本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件)
上篇回顾: ArkTS开发系列之导航 (2.7动画) 本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件) 一、知识储备 1. 触屏事件:包括点击事件、拖拽事件、触摸事件。 点击事件 Button()....onClick(…...
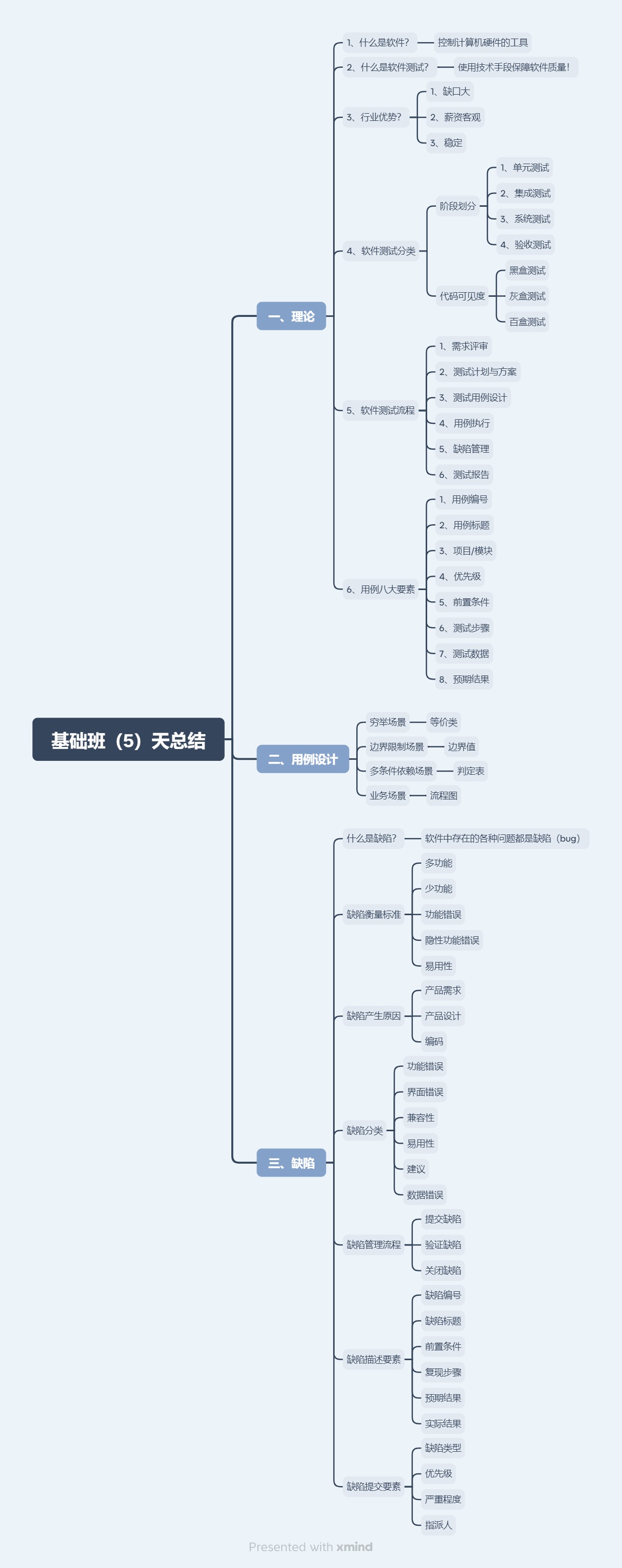
测试的基础知识大全【测试概念、分类、模型、流程、测试用例书写、用例设计、Bug、基础功能测试实战】
测试基础笔记 Day01阶段⽬标⼀、测试介绍⼆、测试常⽤分类2.1 阶段划分单元测试集成测试系统测试验收测试 2.2 代码可⻅度划分⿊盒测试:主要针对功能(阶段划分->系统测试)灰盒测试:针对接⼝测试(阶段划分->集成测…...
Power Apps
目录 一、引言1、Power Apps2、应用场景3、Power Apps的优势与前景4、补充 二、数据源介绍1、SharePoint2、Excel3、Dataverse4、SQL5、补充(1)OneDrive 三、Power Apps应用类型1、画布应用2、模型驱动应用3、网站 Power Pages 四、Power Automate五、Po…...

qt图像处理-将OpenCV的cv::Mat类型转换为QImage类型
在使用Qt进行图像处理时,经常需要将OpenCV的cv::Mat类型转换为QImage类型。以下是几种有效的方法,可以根据具体情况选择合适的方法进行转换。 方法一:直接使用QImage构造函数 这种方法直接使用QImage的构造函数,通过传递cv::Mat的指针和相关参数来创建QImage对象。这种方…...

代码随想录训练营第十八天 530二叉搜索树的最小绝对差 501二叉搜索树中的众数 236二叉树的最近公共祖先
第一题: 原题链接:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode) 思路: 使用中序遍历的方式:左中右。 定义一个pre节点来存放当前节点的前一个节点。 在中序的时候处理递归逻辑: 首先先向…...

微信小程序之横向列表展示
效果图 参考微信小程序可看 代码: <view class"lbtClass"><view class"swiper-container"><scroll-view class"swiper" scroll-x"true" :scroll-left"scrollLeft"><block v-for"(six…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...
