Javascript高级程序设计(第四版)--学习记录
var关键字:定义变量同时可以进行赋值
var message="hello" message = 10可以改变保存的值,也可以改变值的类型,但是不推荐这样写。
- var声明的变量会成为包含它的函数的局部变量。
function test(){ var message = "hello"; } test(); console.log(message);//出错
- var声明提升:变量会自动提升到函数作用域顶部,函数作用域。
function test(){ console.log(message); var message = "hello"; } test();//undefined //等价于以下代码 function test(){ var message; console.log(message); message = "hello" } test();
let关键字:定义变量同时可以赋值。
let message = "hello"
- let不允许同一个块作用域中出现冗余声明
let message; let message;//标识符已经声明过了
- let存在暂时性死区即不存在变量提升
console.log(message);//ReferenceError:message没有定义 let message = "hello";
- let在全局作用域中声明的变量不会成为window对象的属性,var声明的变量则会。
var name = "Jason"; console,log(window.name);// 'Jason'let age = 42; console.log(age);// undefined
const关键字:声明变量并同时赋值且值不允许修改。
const message;//出错 const message = 'hello'; message = Jason';//TypeError:给常量赋值const name = 'Jason'; const name = 'Jason';//SyntaxError:不允许重复声明
数据类型:
- 基本数据类型:Undefined、Null、Boolean、Number、String、Symbol
- 复杂数据类型:Object
相关文章:
--学习记录)
Javascript高级程序设计(第四版)--学习记录
var关键字:定义变量同时可以进行赋值 var message"hello" message 10 可以改变保存的值,也可以改变值的类型,但是不推荐这样写。 var声明的变量会成为包含它的函数的局部变量。 function test(){ var message "hello";…...

DVWA-CSRF-samesite分析
拿DVWA的CSRF为例子 接DVWA的分析,发现其实Impossible的PHPSESSID是设置的samesite1. 参数的意思参考Set-Cookie SameSite:控制 cookie 是否随跨站请求一起发送,这样可以在一定程度上防范跨站请求伪造攻击(CSRF)。 下面用DVWA CS…...

代码随想录训练营Day48
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、买卖股票的最佳时机4二、买卖股票的最佳时机含冷冻期三、买卖股票含手续费 前言 提示:这里可以添加本文要记录的大概内容: 今天是…...
:导航守卫_renderroutes)
React进阶(五):导航守卫_renderroutes
在《React进阶(四):路由介绍》博文中,介绍了React路由相关知识,在实际项目开发过程中,路由之间的跳转必定涉及权限、用户是否登陆等限定条件的判定,故需要导航守卫来完成这一事项。 在实现reac…...

Python基础系列教程:从零开始学习Python
Python有很多功能强大的机器学习和大数据分析包,适合对大数据和人工智能感兴趣的同学学习。要想了解一门语言,首先需要了解它的语法。本文将介绍Python的一些基础语法,包括数据类型、变量类型、条件控制、循环结构等内容。废话少说࿰…...

deepl翻译的PDF文档保护密码解除
1、首先将后缀名(.docx)修改为压缩包格式(.zip)。 2、修改解密word加密.py里zip的位置,和新生成的zip的位置和名称 import zipfile import xml.etree.ElementTree as ET import os import shutil# 定义文件路径 zip_file_path rC:\Users\Administrator\Desktop\新…...

LeetCode 算法:二叉树的直径 c++
原题链接🔗:二叉树的直径 难度:简单⭐️ 题目 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的 长度 。这条路径可能经过也可能不经过根节点 root 。 两节点之间路径的 长度 由…...
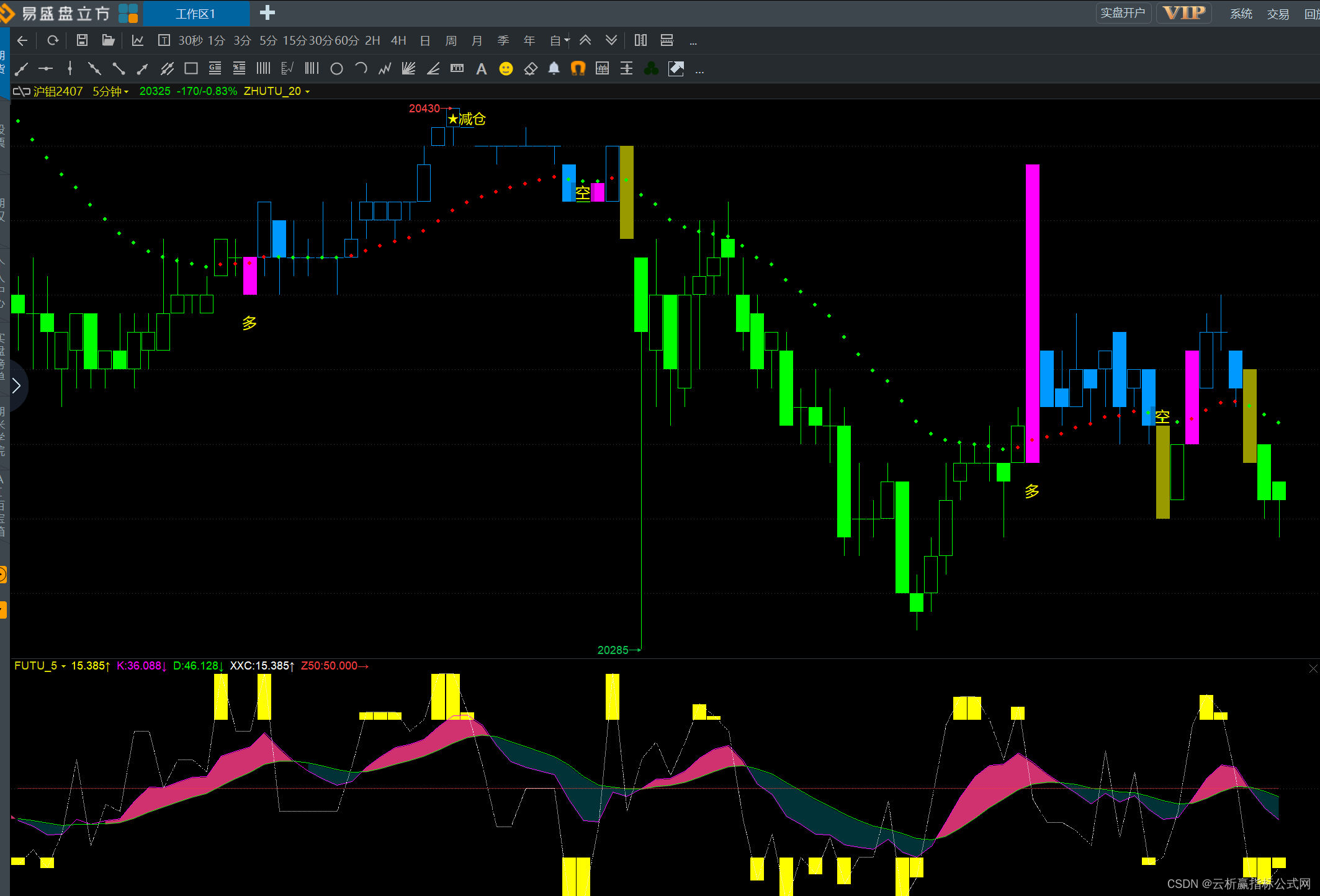
盘立方期货Kdj幅图指标公式源码
盘立方期货Kdj幅图指标公式源码: N:250; WR1:100-100*(HHV(HIGH,N)-CLOSE)/(HHV(HIGH,N)-LLV(LOW,N)),DOT,COLORLIGHTGREEN; EW:EMA(WR1,5); STICKLINE(WR1<20,WR1,20,1,0),COLORYELLOW; STICKLINE(WR1>80,WR1,80,1,0),COLORYELLOW; RSV:(CLOSE-LLV(LOW…...
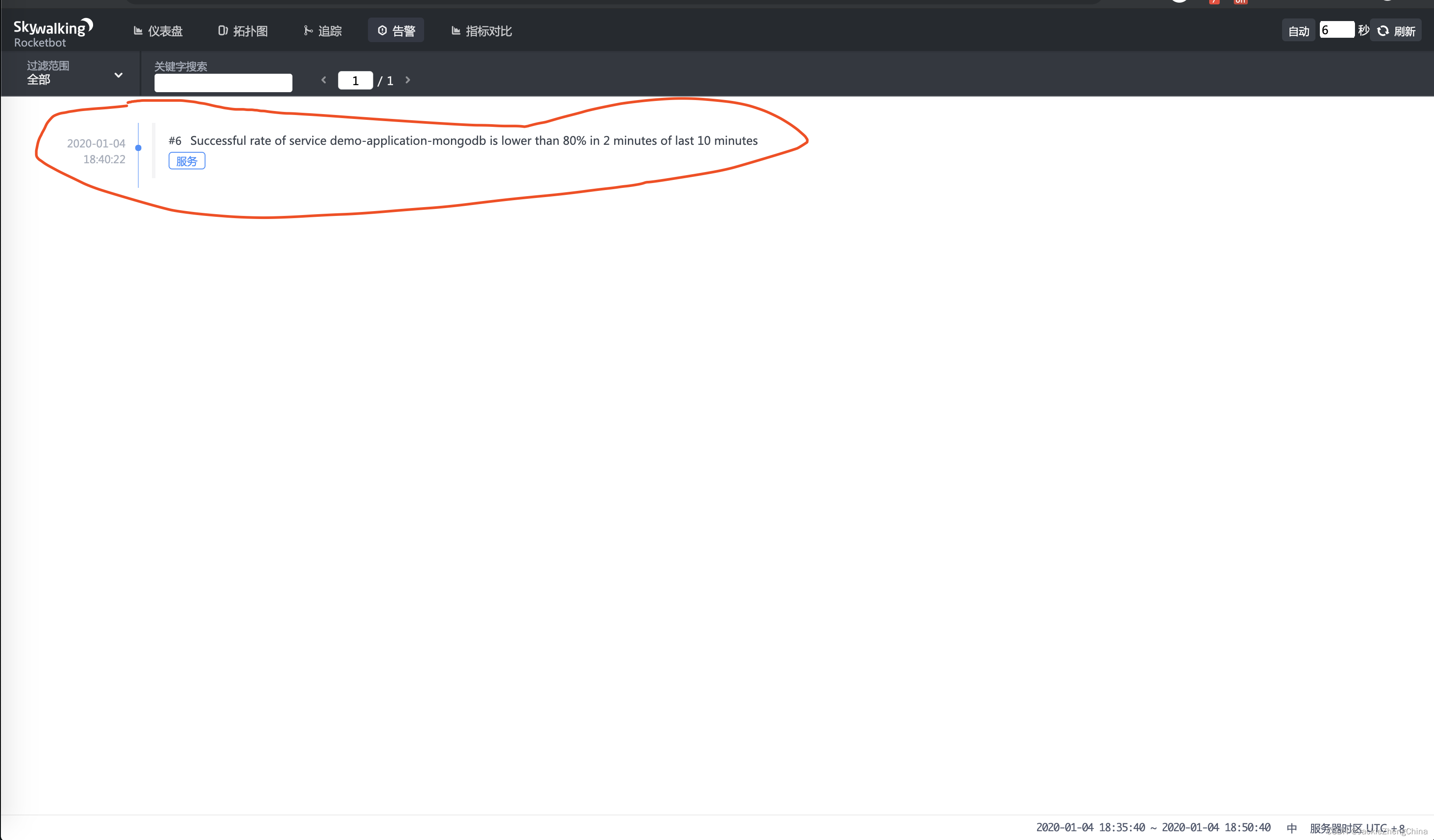
SkyWalking 极简入门
1. 概述 1.1 概念 SkyWalking 是什么? FROM Apache SkyWalking 分布式系统的应用程序性能监视工具,专为微服务、云原生架构和基于容器(Docker、K8s、Mesos)架构而设计。 提供分布式追踪、服务网格遥测分析、度量聚合和可视化一体…...
)
本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件)
上篇回顾: ArkTS开发系列之导航 (2.7动画) 本篇内容:ArkTS开发系列之事件(2.8.1触屏、键鼠、焦点事件) 一、知识储备 1. 触屏事件:包括点击事件、拖拽事件、触摸事件。 点击事件 Button()....onClick(…...
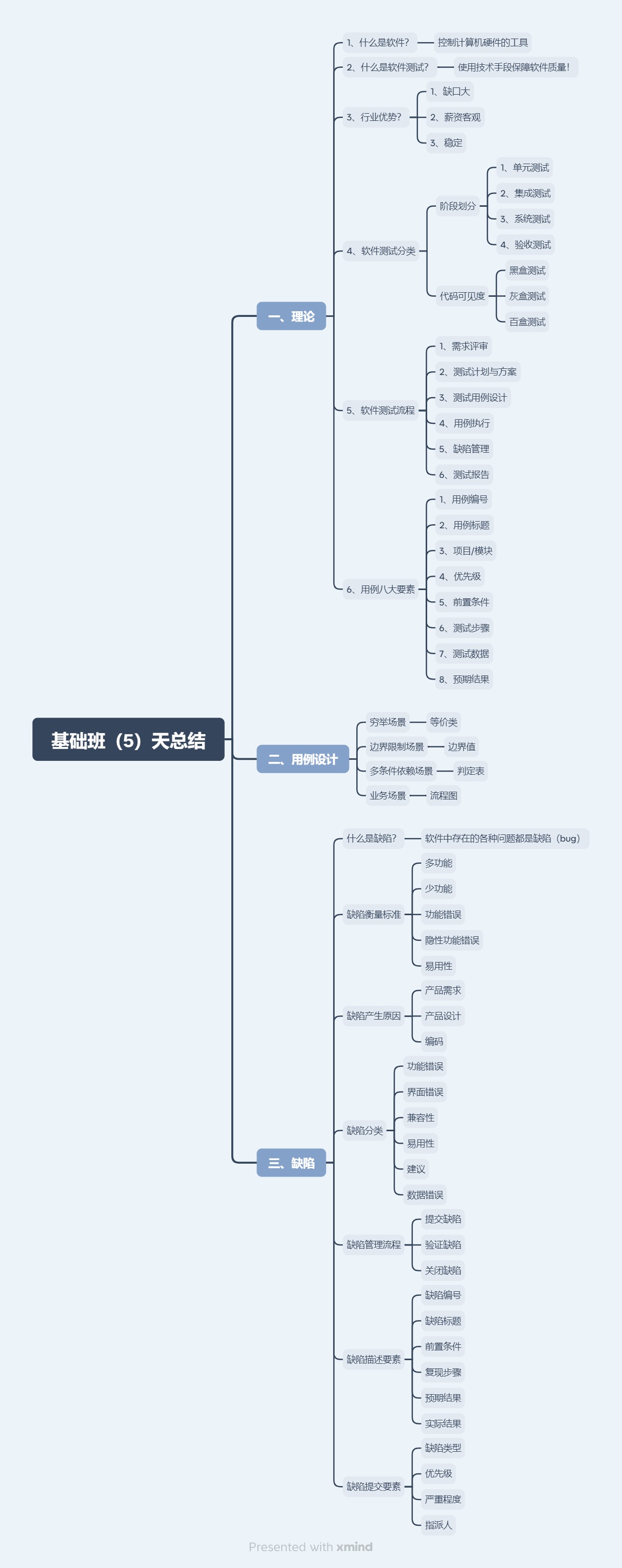
测试的基础知识大全【测试概念、分类、模型、流程、测试用例书写、用例设计、Bug、基础功能测试实战】
测试基础笔记 Day01阶段⽬标⼀、测试介绍⼆、测试常⽤分类2.1 阶段划分单元测试集成测试系统测试验收测试 2.2 代码可⻅度划分⿊盒测试:主要针对功能(阶段划分->系统测试)灰盒测试:针对接⼝测试(阶段划分->集成测…...
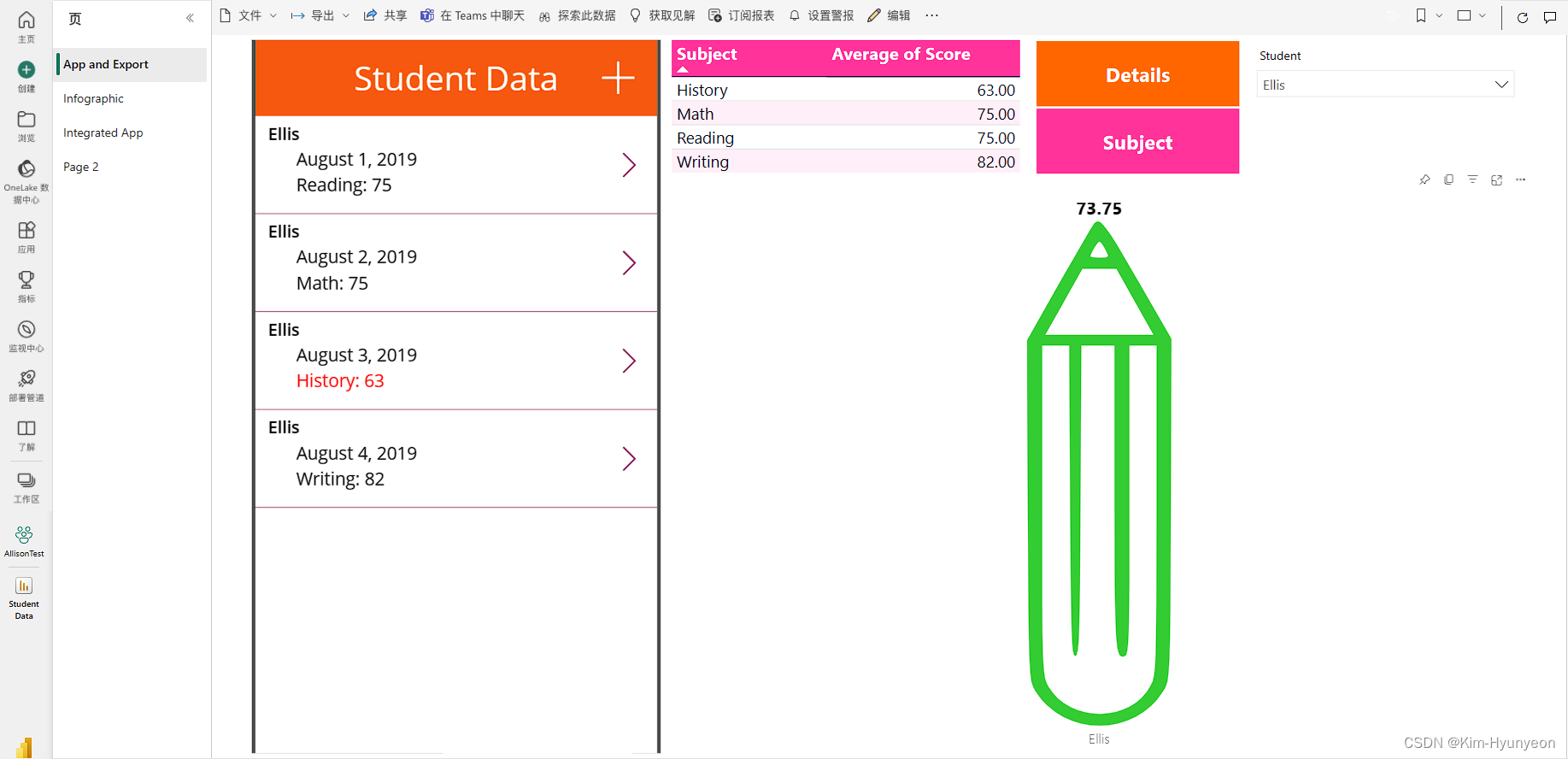
Power Apps
目录 一、引言1、Power Apps2、应用场景3、Power Apps的优势与前景4、补充 二、数据源介绍1、SharePoint2、Excel3、Dataverse4、SQL5、补充(1)OneDrive 三、Power Apps应用类型1、画布应用2、模型驱动应用3、网站 Power Pages 四、Power Automate五、Po…...

qt图像处理-将OpenCV的cv::Mat类型转换为QImage类型
在使用Qt进行图像处理时,经常需要将OpenCV的cv::Mat类型转换为QImage类型。以下是几种有效的方法,可以根据具体情况选择合适的方法进行转换。 方法一:直接使用QImage构造函数 这种方法直接使用QImage的构造函数,通过传递cv::Mat的指针和相关参数来创建QImage对象。这种方…...

代码随想录训练营第十八天 530二叉搜索树的最小绝对差 501二叉搜索树中的众数 236二叉树的最近公共祖先
第一题: 原题链接:530. 二叉搜索树的最小绝对差 - 力扣(LeetCode) 思路: 使用中序遍历的方式:左中右。 定义一个pre节点来存放当前节点的前一个节点。 在中序的时候处理递归逻辑: 首先先向…...

微信小程序之横向列表展示
效果图 参考微信小程序可看 代码: <view class"lbtClass"><view class"swiper-container"><scroll-view class"swiper" scroll-x"true" :scroll-left"scrollLeft"><block v-for"(six…...
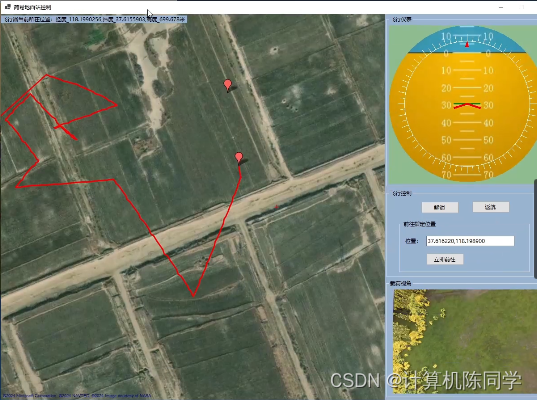
无人机巡检小羊仿真
详细视频地址 仿真效果 可视化三维仿真 gazebo物理仿真 px4 飞控仿真 仿qgc简易地面站 详细视频地址...

springboot redission 分布式锁
Spring Boot中使用Redisson实现分布式锁的方法如下: 1. 首先,需要在项目中引入Redisson依赖。在pom.xml文件中添加以下依赖: xml <dependency> <groupId>org.redisson</groupId> <artifactId>redisson<…...

Vuex中的重要核心属性
Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 Vuex 的核心属性包括: State: State 是 Vuex 存储数据的地方,类似于组件中的 data。它…...

Redis哨兵集群搭建
一、安装Redis 1.安装依赖 yum install -y gcc tcl2.将Redis压缩包解压到对应的目录 tar -zxvf redis-2.8.0.tar.gz mv redis-2.8.0 /usr/local3.编译 cd /usr/local/redis-2.8.0 make && make install4.配置redis.conf # 任意ip都可以访问 bind 0.0.0.0 # 关闭保…...

网络爬虫requests库使用指南
目录 引言 安装requests库 基本用法 发送GET请求 发送POST请求 处理请求头和Cookies 设置请求头 使用Cookies 会话管理 异常处理 流式上传和下载 结语 引言 在Python中进行HTTP请求时,requests库是一个强大且易于使用的第三方库。它允许你发送各种HTTP请…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

select、poll、epoll 与 Reactor 模式
在高并发网络编程领域,高效处理大量连接和 I/O 事件是系统性能的关键。select、poll、epoll 作为 I/O 多路复用技术的代表,以及基于它们实现的 Reactor 模式,为开发者提供了强大的工具。本文将深入探讨这些技术的底层原理、优缺点。 一、I…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...
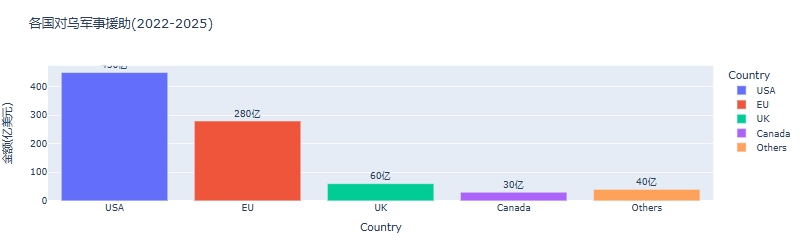
python可视化:俄乌战争时间线关键节点与深层原因
俄乌战争时间线可视化分析:关键节点与深层原因 俄乌战争是21世纪欧洲最具影响力的地缘政治冲突之一,自2022年2月爆发以来已持续超过3年。 本文将通过Python可视化工具,系统分析这场战争的时间线、关键节点及其背后的深层原因,全面…...
