PyTorch实战:借助torchviz可视化计算图与梯度传递
文章目录
-
- Tensor计算的可视化(线性回归为例)
- 如何使用可视化库torchviz
-
- 安装graphviz软件
- 安装torchviz库
- 使用 torchviz.make_dot()
- 安装graphviz软件
- Tensor计算的可视化(线性回归为例)
在学习Tensor时,将张量y用张量x表示,它们背后会有一个函数表达关系,y的
grad_fn
会被赋予一个对应的函数。先定义的x是一个叶子节点,将所有Tensor节点的计算连接起来就可以用一个
有向无环图
(DAG)来表示,称为
计算图
(Computational graphs)。
Computational graphs 例图:

有了图之后就可以清晰直观地理解这个模型的计算过程(forward)和梯度传递(backward)。
在初学线性回归模型的时候,同样可以把手写的线性回归模型以计算图的形式可视化表示出来,可便于深入理解代码背后的计算过程。
Tensor计算的可视化(线性回归为例)
使用的同样是“动手学深度学习的
线性回归从零实现
的例子”。
该模型的定义函数和损失函数为:
def linreg(X, w, b):return torch.mm(X, w) + bdef squared_loss(y_hat, y): return (y_hat - y.view(y_hat.size())) ** 2 / 2在训练模型时定义的损失函数为:
net = linreg
loss = squared_loss
# 因为loss完是一个10*1的张量,所以需要sum一下转换成标量以便标量求导
l = loss(net(X, w, b), y).sum()我们可以将损失函数 l 的计算图表示出来,以
理解梯度是怎么传播
的。
这里使用torchviz的make_dot()函数将这些计算节点表示出来,在
例子
末尾添加代码,执行:
data_iter1 = data_iter(batch_size, features, labels)
X, y = next(data_iter1) # 另取一个batch数据l = loss(net(X, w, b), y).sum()# 判断各节点是否是叶子节点
print(X.is_leaf)
print(y.is_leaf)
print(w.is_leaf)
print(b.is_leaf)
print(l.is_leaf)
print(X.grad_fn)
print(l.grad_fn)from torchviz import make_dot
make_dot(l.mean())
# 这里添加mean()是对之前的取sum()求平均,具体可以参考 自动求导的实现 相关知识。结果显示:
True
True
True
True
False
None
<SumBackward0 object at 0x000001DC230C7DA0>

下面可以对该线性回归模型的损失函数进行分析
:
可以看到X,y,w,b都是计算图中的叶子节点,l表示计算流终点,它不是叶子节点。
X是叶子节点,没有
grad_fn
,即没有创建该Tensor的Function。
l代表父节点,它有创建该Tensor的Function,可以看到它的
grad_fn
是
SumBackward0
,也就是图中倒数第三个节点。
图中可以清晰地看到计算过程和梯度传递的可视化,包含了计算图的信息。左上蓝色框是shape为(2,1)的权重w,右上是b。因为X和y没有被赋予梯度,所以不出现在图中。
箭头的方向是计算执行的朝向,每次计算朝向下一个带
grad_fn
的节点,梯度则根据这个流向进行反传。
以上是最简单的线性模型,在之后的神经网络模型中,同样可以使用类似的方法对
模型
或者
损失函数
等计算过程进行可视化分析。可视化工具torchviz的安装使用见下。
如何使用可视化库torchviz
可视化需要安装torchviz库和graphviz软件。
安装graphviz软件
- 下载:
https://graphviz.org/download/
选择对应的平台的安装方式,Windows是下载安装包。
下载好以后根据向导安装,注意根据提示把graphviz添加到环境变量中去。
2. 安装成功后再cmd界面输入
dot -version
可显示版本信息

3. 安装python库:
pip install graphviz
安装torchviz库
pip install torchviz
使用 torchviz.make_dot()
使用 torchviz.make_dot() 函数就可以将Tensor计算和梯度传播过程可视化了。推荐在jupyter环境下使用。
使用方法:直接在make_dot()中传入待分析的Tensor变量即可,比如上面的例子。
如果想自行控制计算图的展示,在jupyter notebook中使用display即可:
dot = torchviz.make_dot(l) # make_dot返回一个dot(一个Diagraph对象)
display(dot)其它进阶使用方法可以参考官方的文档:
地址
。
参考文献:
https://pytorch.org/blog/computational-graphs-constructed-in-pytorch/
相关文章:

PyTorch实战:借助torchviz可视化计算图与梯度传递
文章目录 Tensor计算的可视化(线性回归为例) 如何使用可视化库torchviz 安装graphviz软件 安装torchviz库使用 torchviz.make_dot() 在学习Tensor时,将张量y用张量x表示,它们背后会有一个函数表达关系,y的 grad_f…...
【软件测试】软件测试入门
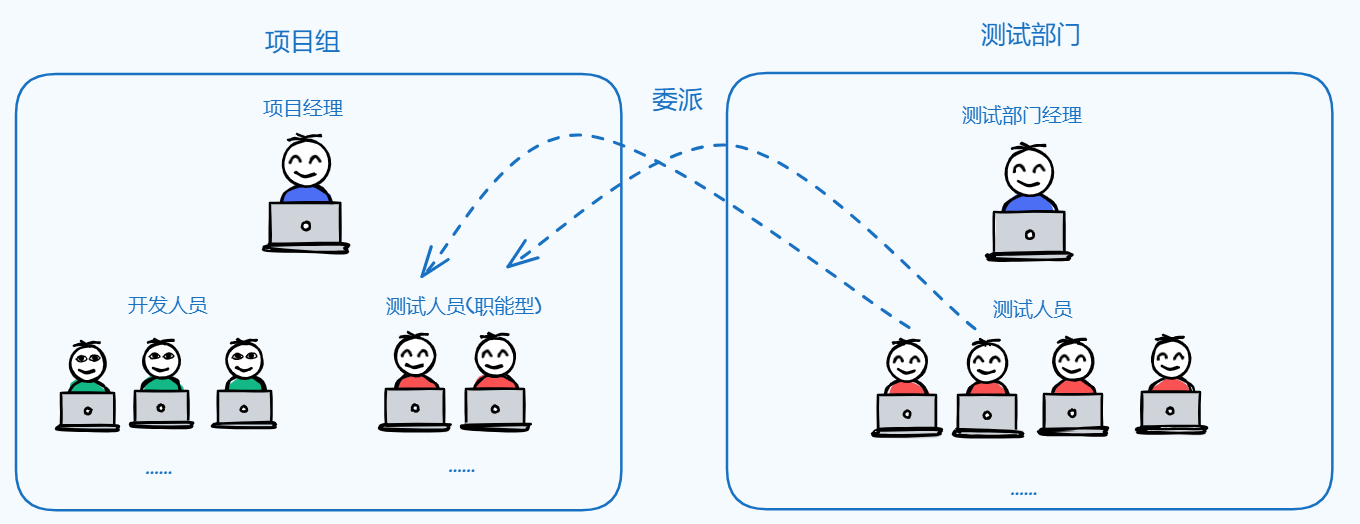
软件测试入门 一、什么是软件测试二、软件测试和软件开发的区别三、软件测试在不同类型公司的定位1. 无组织性2. 专职 OR 兼职3. 项目性VS.职能性4.综合型 四、一个优秀的软件测试人员具备的素质1. 技能相关2. 非技能相关 一、什么是软件测试 最常见的理解是:软件测…...

Windows操作防火墙命令
Windows操作防火墙命令 启用防火墙: netsh advfirewall set allprofiles state on禁用防火墙: netsh advfirewall set allprofiles state off添加新的入站规则允许端口80(HTTP): netsh advfirewall firewall add r…...

二维数组的知识
二维数组: 1.同种数组类型的集合 2.连续的内存空间 3.由多个一维数组组成 定义方式: 存储类型 数据类型 数组名[常量表达式(行数)][常量表达式(列数)]࿱…...

HR3.0时代,人力资本效能如何进化?| 易搭云DHR
宏观经济增速放缓、市场竞争激烈,对各行各业、各种岗位都面临更大挑战,如何降本增效还是每个企业主的关注焦点。 企业的主要支出往往是员工成本,总体上超过企业总开支的75%,轻资产类型的企业甚至可能超80%,但裁员、加班…...
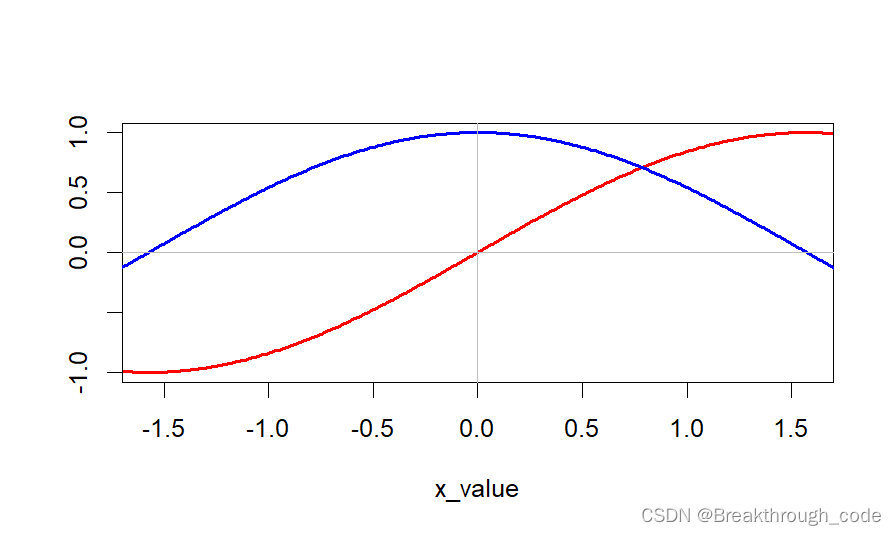
R语言做图
目录 1. 图形参数 2. 低级图形 3. 部分高级图形 参考 1. 图形参数 图形参数用于设置图形中各种属性。 有些参数直接用在绘图函数内,如plot函数可以用 pch(点样式)、col(颜色)、cex(文字符号大小倍数&…...

跟着我一步两步三步,用开源方式将AI带入企业
“AI有开源派与闭源派,你挺哪一派?”这是红帽公司针对媒体所做的一次小调查。结果显示,坚定的开源派占50%,挺闭源的仅有5.56%。如果是你,又会怎样选择? 如何才能让AI在企业中快速平稳落地,并且开…...
天途重磅推出无人机教管平台3.1版及飞课APP
天途无人机教管平台,是一款为院校和培训机构等企业级客户提供的公开版无人机在线培训系统,包含后台管理的【教管平台】和终端的【掌上天途APP】。 天途历经4年上百次调研和迭代打磨,已为一百多家院校和培训机构等企业级客户解决了无人机教学和…...
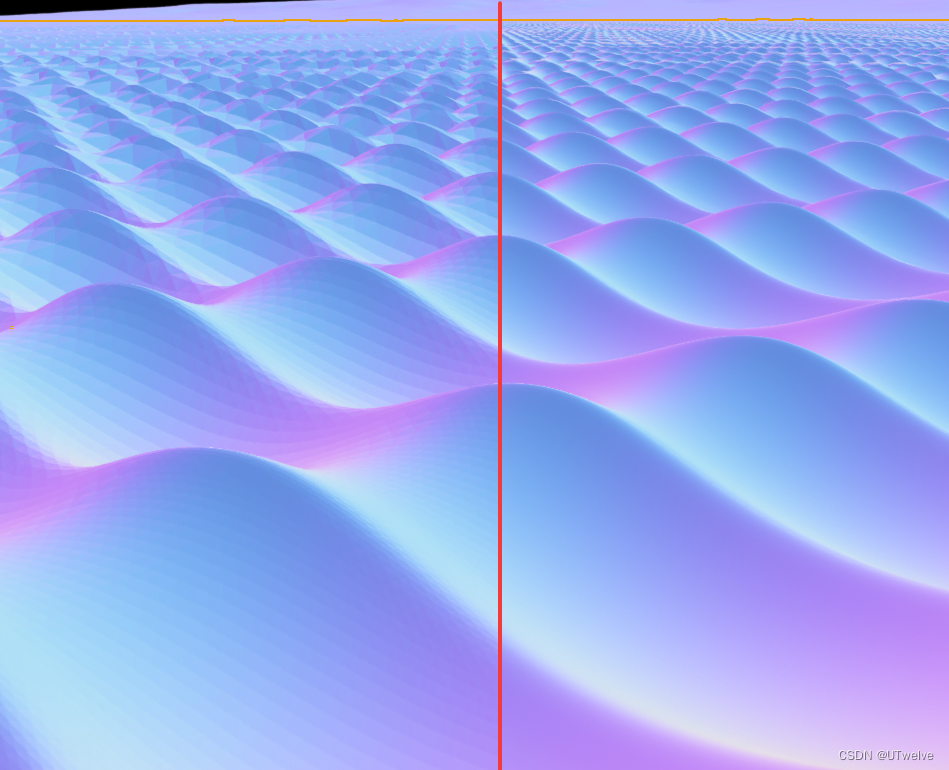
虚幻引擎 Gerstner Waves -GPU Gems 从物理模型中实现有效的水体模拟
这篇文章重点在于结合GPU Gems一书中有关Gerstner Waves 的数学公式,在虚幻引擎中复现正确的Gerstner Waves和正确的法线 文中内容整理自书中,并附带我的理解,与在虚幻引擎中的实现,可以参考原文看这篇文章,原文网上很…...

Labview_网络流
网络流的介绍 网络流是一种易于配置、紧密集成的动态通信方法,用于将数据从一个应用程序传输到另一个应用程序,其吞吐量和延迟特性可与 TCP 相媲美。但是,与 TCP 不同的是,网络流直接支持任意数据类型的传输,而无需先…...

让生产管理变简单
随着业务的发展,工厂每天要处理很多订单,还要统筹安排各部门工作以及协调上下游加工企业,生产管理问题也随之而来。 1.销售订单评审困难、无法及时抓取到历史数据做参考。由于数据的不及时性、不准确性无法为正常的生产和采购提供数据支撑。同…...

MySQL与SQLite的区别
MySQL 和 SQLite 是两种常见的关系型数据库管理系统,但它们在设计目标、架构和使用场景上有显著的区别。以下是它们的主要区别: 1. 架构与模式 MySQL: 客户端/服务器模式:MySQL 采用 C/S 架构,数据库服务器运行在一…...
Hi3861 OpenHarmony嵌入式应用入门--LiteOS Event
CMSIS 2.0接口使用事件标志是实时操作系统(RTOS)中一种重要的同步机制。事件标志是一种轻量级的同步原语,用于任务间或中断服务程序(ISR)之间的通信。 每个事件标志对象可以包含多个标志位,通常最多为31个&…...
Centos+Jenkins+Maven+Git 将生成的JAR部署到Jenkins服务器上
背景:前一篇写的是Jenkins和项目应用服务器不在同一个服务器上。但是有的公司可能不会给Jenkins单独弄一个服务器。可能就会出现Jenkins就搭建在某一个应用服务器上。这种情况的参考如下的操作。 1、登录 没有安装的参考下面的安装步骤先安装: Jenkins安装手册 输入账号、…...
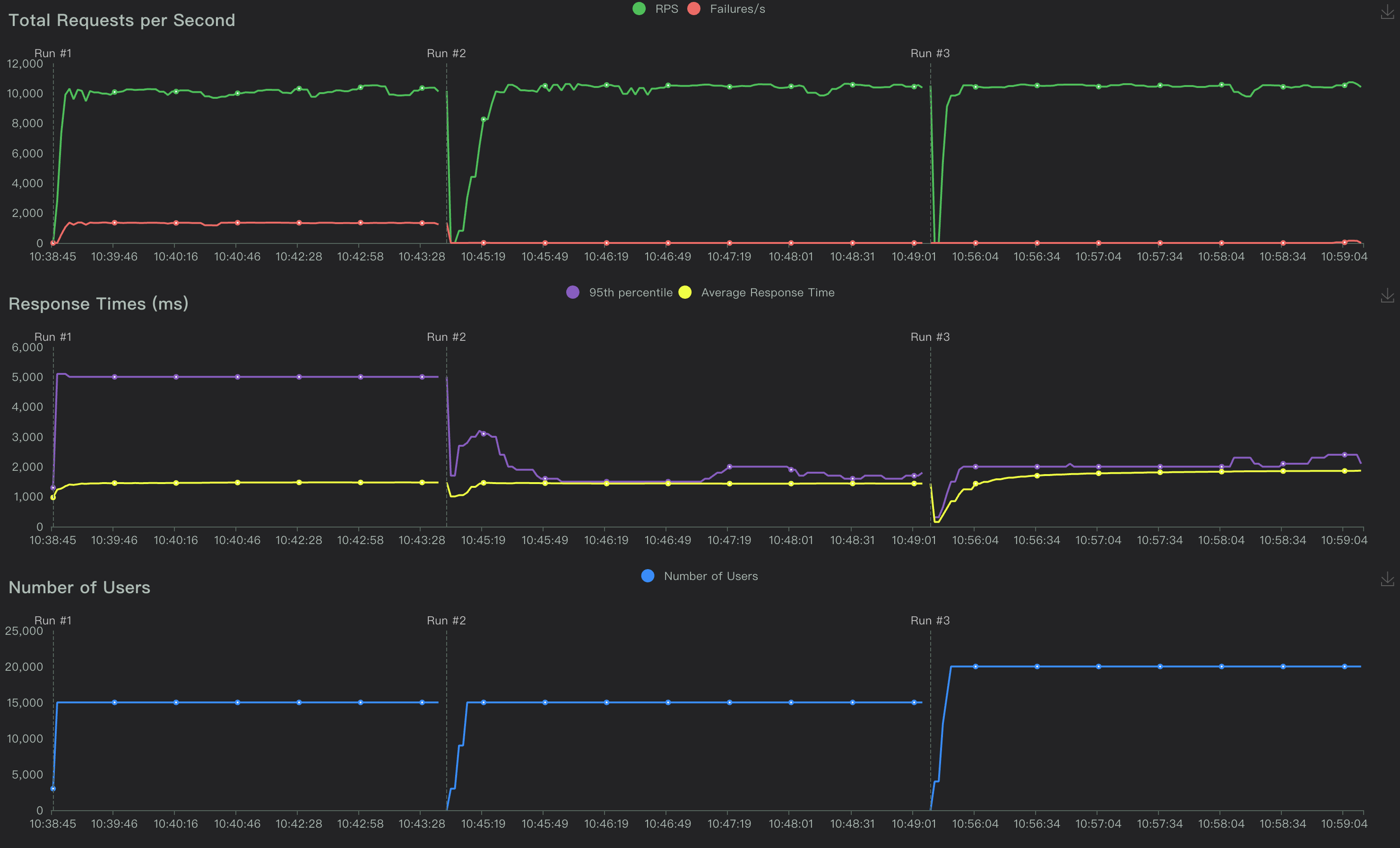
性能评测系列(PT-010):Spring Boot + MySQL,高并发insert
一、测试概述 测试场景 场景编号: PT-010场景描述: Java应用,MySQL单表写测试目的:指定规格、配置、环境下,Java应用数据库简单写场景负载能力评估。(不含调优,所测结果未必是最优结果&#x…...

网站改成HTTPS方法
网站改成HTTPS只要网站没有特殊性的要求,绝大部分网站很轻松的就可以完成,尤其是CMS类似的网站系统或者自助搭建的网站(比如:这种网站可以在网站后台一次性安装并且生效)。 基本要求 将网站改成HTTPS有2个前提&#…...
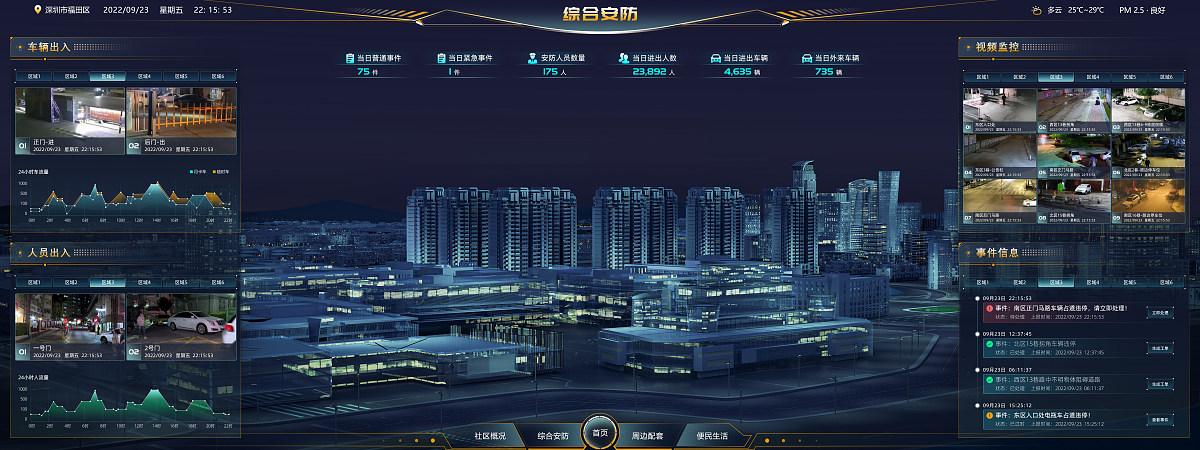
智慧社区:居民幸福生活的保底线,价值非常大。
大屏应该能够显示社区内的关键数据,如人流量、车辆数量、垃圾分类情况等。这些数据可以通过图表、数字、地图等形式展示,以便居民和管理者能够直观地了解社区的情况。 智慧社区可视化大屏成为一个有益于社区管理和居民生活的工具,提供实时、准…...
《昇思25天学习打卡营第1天|NapKinG》
昇思MindSpore 学习昇思大模型的第一天,先了解一下此模型的架构,设计理念,以及层次结构,昇思大模型(MindSpore)的优点有很多,易开发,高效执行,全场景统一部署,是一个全场景深度学习框架 易开发的具体表现为API友好,调试难度低,高效执行包括计算效率,数据预处理效率和分布式训练…...
Java项目毕业设计:基于springboot+vue的幼儿园管理系统
数据库:MYSQL5.7 **应用服务:Tomcat7/Tomcat8 使用框架springbootvue** 项目介绍 管理员;首页、个人中心、用户管理、教师管理、幼儿信息管理、班级信息管理、工作日志管理、会议记录管理、待办事项管理、职工考核管理、请假信息管理、缴费信息管理、幼儿请假管理…...
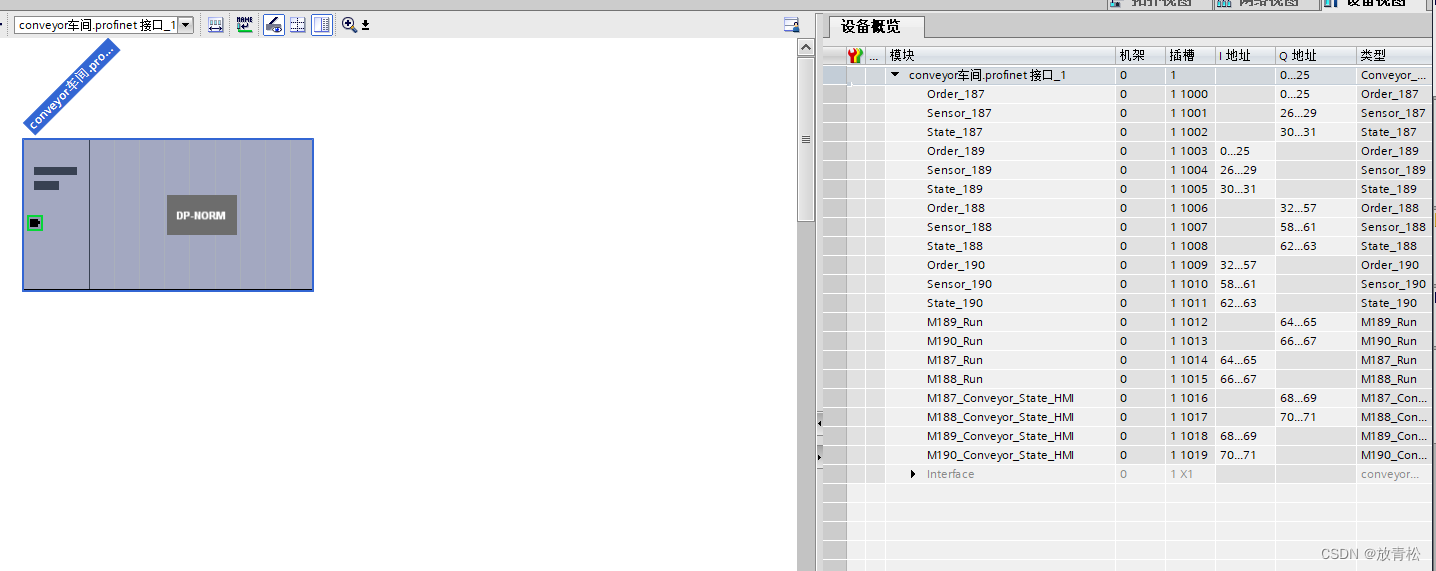
CPU1511作为CPU1513的智能IO设备
一、把一个IO控制器作为另一个IO控制器的IO设备来使用 1、在智能设备通信里定义好传输区后,导出GSD文件 2、在另一个项目程序内添加GSD文件 3、当作PLC的IO设备组态,并连接至PLC_1 4、在右侧更改I区、Q区地址与名称 5、硬件编译并下载,此…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...
