LeetCode —— 只出现一次的数字
只出现一次的数字 I

本题依靠异或运算符的特性,两个相同数据异或等于0,数字与0异或为本身即可解答。代码如下:
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for (auto e : nums){ret ^= e;}return ret;}
};
只出现一次的数字 II

官方使用位运算题解代码如下:
class Solution {
public:int singleNumber(vector<int>& nums) {int ans = 0;for (int i = 0; i < 32; ++i) {int total = 0;for (int num: nums) {total += ((num >> i) & 1);}if (total % 3) {ans |= (1 << i);}}return ans;}
};
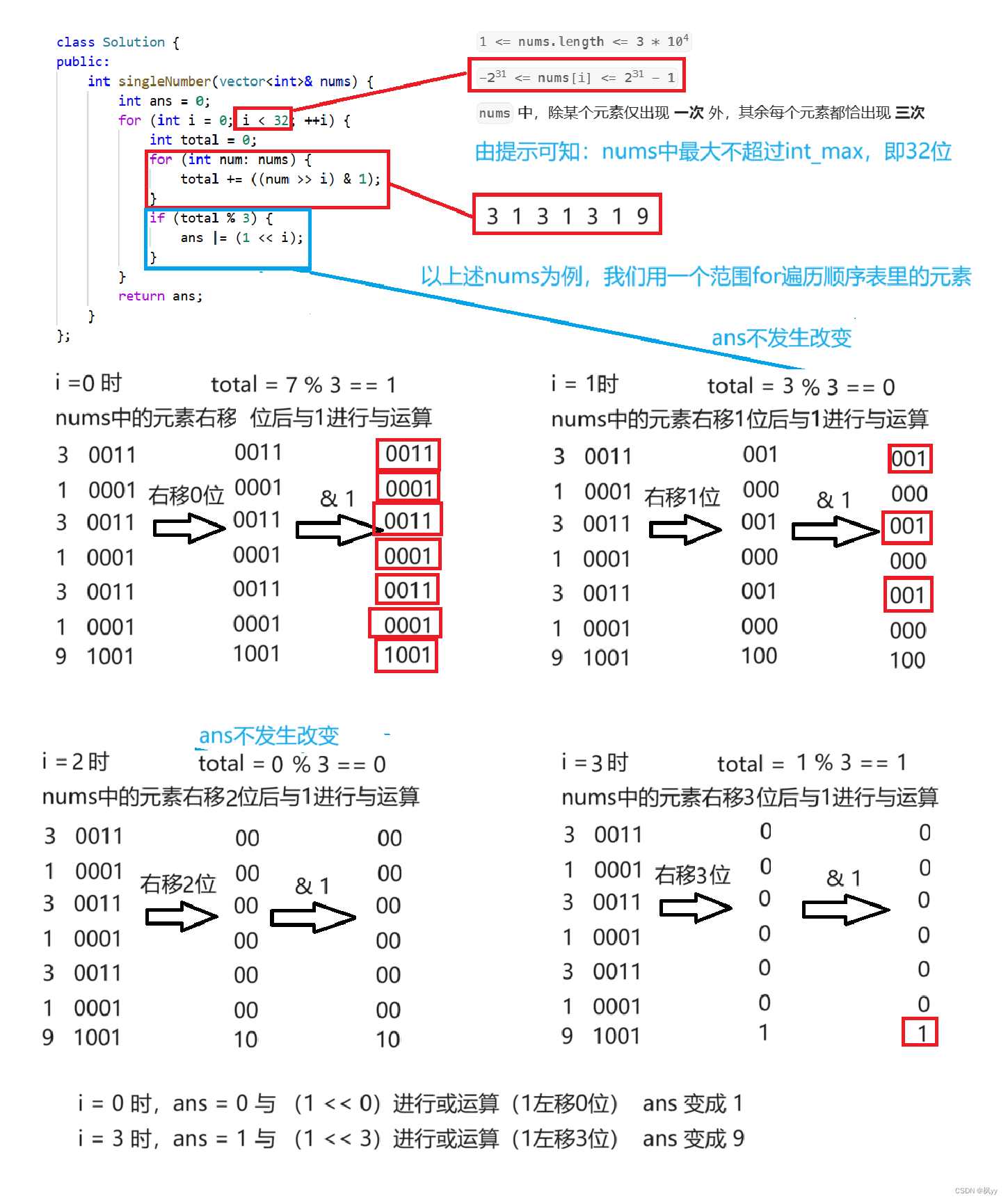
为什么可以这样实现呢?博主也是想了好久,现在解释原理:
- 若顺序表中的元素个数为奇数,那么一定有 2n 组出现 3 次的数和1个只出现一次的数组成,右移n位,由于出现 3 次的数是偶数个,那么与1进行与运算并相加后,必定为3的倍数,如果模3不等于0,只有一种可能:只出现一次的数为1使total不能被整除,说明只出现一次的数第 i 位为1,反之为0。
- 若顺序表中的元素个数为偶数,那么一定有2n + 1组出现三次的数和1个只出现一次的数组成,右移n位,由于出现 3 次的数是奇数个,那么与1进行与运算并相加后,必定为3的倍数,如果模 3 不等于 0 ,只有一种可能:只出现一次的数为1使total不能被整除,说明只出现一次的数第 i 位为1,反之为0。
只出现一次的数字 III

本人选择了一个较为好理解的答案, 题解大神(灵茶山艾府)使用位运算题解代码如下:
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {// 负数在计算机是补码的形式存在// 无符号取负数就是取反加一unsigned int x = 0;for (auto e : nums){x ^= e;}int lowbit = x & -x;// 此方法可以算出最低比特位 vector<int> ans(2);for (auto f : nums){ans[(f & lowbit) != 0] ^= f;}return ans;}
};
看完图之后是否理解得更加深刻了呢?个人觉得第二次遍历相当巧妙,下面看大佬给出的解释:

希望本篇文章对你有帮助,有问题请在评论区指正,感谢阅读。
相关文章:

LeetCode —— 只出现一次的数字
只出现一次的数字 I 本题依靠异或运算符的特性,两个相同数据异或等于0,数字与0异或为本身即可解答。代码如下: class Solution { public:int singleNumber(vector<int>& nums) {int ret 0;for (auto e : nums){ret ^ e;}return ret;} };只出…...
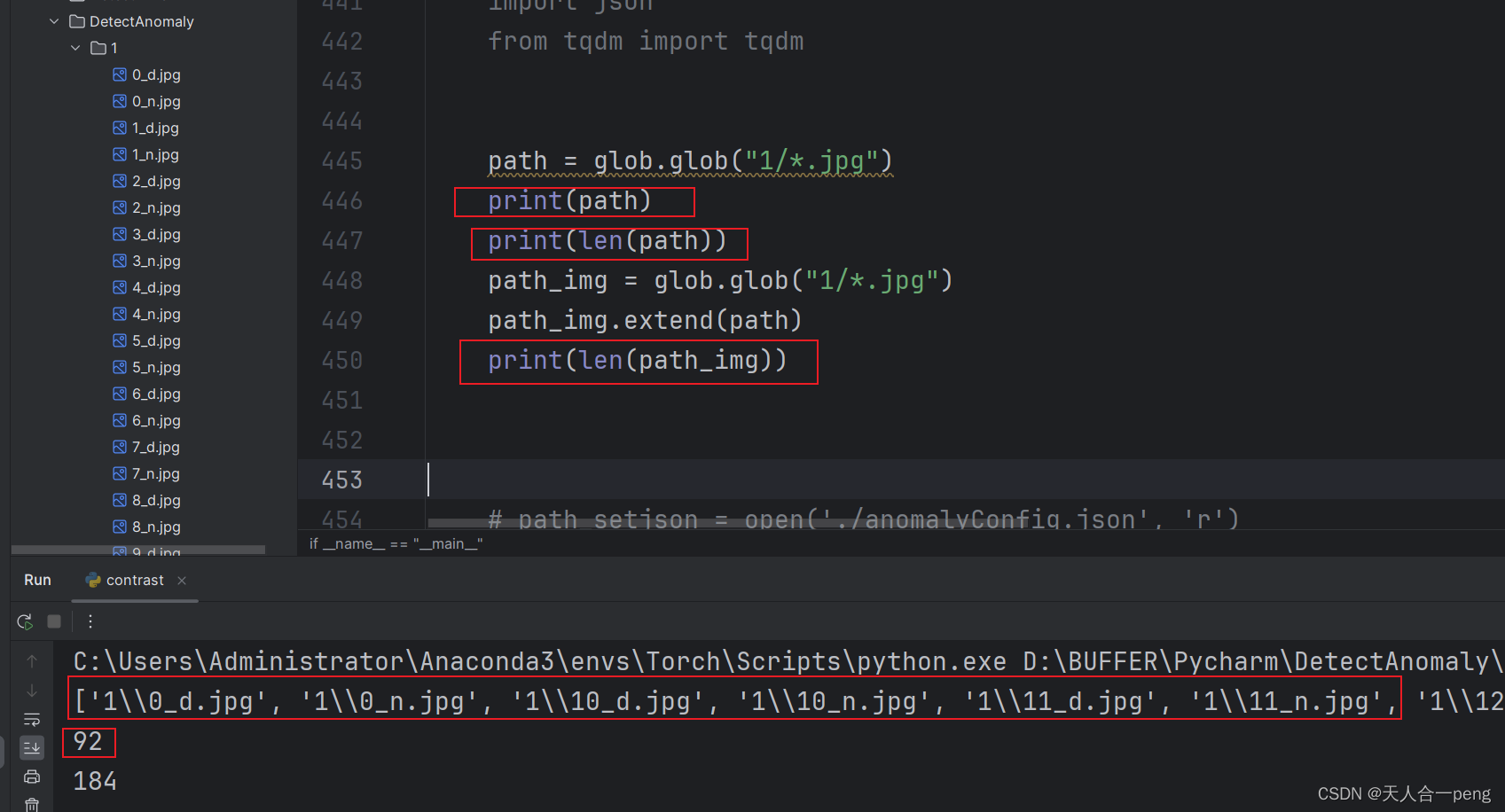
python遍历文件夹中所有图片
python遍历文件夹中的图片-CSDN博客 这个是之前的版本,现在这个版本会更好,直接进来就在列表中 path glob.glob("1/*.jpg")print(path)print(len(path))path_img glob.glob("1/*.jpg")path_img.extend(path)print(len(path_img))…...

速盾:DDOS能打死高防ip吗?
DDoS攻击是一种利用大量计算机或设备发起的分布式拒绝服务攻击。它的目标是通过发送大量流量或请求,使目标服务器或网络资源无法正常工作。高防IP是一种具有强大防御能力的网络服务,能够抵御各种形式的网络攻击,包括DDoS攻击。然而࿰…...

3dsMax怎样让渲染效果更逼真出色?三套低中高参数设置
渲染是将精心构建的3D模型转化为逼真图像的关键步骤。但要获得令人惊叹的渲染效果,仅仅依赖默认设置是不够的。 实现在追求极致画面效果的同时,兼顾渲染速度和时间还需要进行一些调节设置,如何让渲染效果更加逼真? 一、全局照明与…...

Android的OverlayFS原理与作用
标签: OverlayFS; Android;Overlay Filesystem; Android的OverlayFS原理与作用 概述 OverlayFS(Overlay Filesystem)是一种联合文件系统,允许将一个或多个文件系统叠加在一起,使它们表现为一个单一的文件系统。Android系统利用OverlayFS来实现动态文件系统的叠加和管…...

奇点临近:人类与智能时代的未来
在信息爆炸的时代,我们每天都被海量的信息所淹没,如何才能在这个嘈杂的世界中找到真正有价值的信息?如何才能利用信息的力量,提升我们的认知水平,重塑我们的未来? 这些问题的答案,或许都能在雷…...
NAS教程丨铁威马如何登录 SSH终端?
适用型号: 所有TNAS 型号 如您有特殊操作需要通过 SSH 终端登录 TNAS,请参照以下指引: (注意: 关于以下操作步骤中的"cd /"的指令,其作用是使当前 SSH/Telnet 连接的位置切换到根目录,以免造成对卷的占用.请不要遗漏它.) Windows…...

2024-06-24 百度地图的使用及gps定位坐标获取
1.百度地图的使用教程 2. 定位功能的实现 第一种:通过h5自带定位获取当前gps坐标 var options {enableHighAccuracy: true,timeout: 5000,maximumAge: 0};function success(pos) {var crd pos.coords;alert(crd.latitude---crd.longitude---crd.accuracy);conso…...

Python二级考试试题②
1. 以下关于程序设计语言的描述,错误的选项是: A Python语言是一种脚本编程语言 B 汇编语言是直接操作计算机硬件的编程语言 C 程序设计语言经历了机器语言、汇编语言、脚本语言三个阶段 D 编译和解释的区别是一次性翻译程序还是每次执行时都要翻…...

安装和使用nvm安装Nodejs
文章目录 安装和使用 nvm1. 安装 nvm2. 重新加载终端配置3. 安装所需的 Node.js 版本4. 使用安装的 Node.js 版本 nvm 常用命令 安装和使用 nvm 以下是安装 nvm 并使用它来安装 Node.js 的步骤: 1. 安装 nvm 首先,您需要安装 nvm。您可以使用 curl 或…...
)
非遗!四川省21市非遗大师工作室申报认定条件程序和认定补贴经费支持(管理办法)
第一章总则 第一条贯彻落实中共中央办公厅、国务院办公厅《关于进一步加强非物质文化遗产保护工作的意见》(厅字〔2021〕31号)、四川省文化和旅游厅等12部门《关于进一步加强非物质文化遗产保护工作的实施意见》(川文旅发〔2022〕25号&#…...

uni-app系列:uni.navigateTo传值跳转
文章目录 1. 使用URL参数2. 使用页面栈注意事项:uni.navigateTo API 参数详细说明回调函数参数 在uni-app中,如果想要通过uni.navigateTo方法跳转到另一个页面并传递参数,可以使用页面路由的URL参数或者页面栈的方式来传递。但是,…...

6.3万美刀BTC的车还能上吗?
原创 | 刘教链 隔夜BTC接连下挫,一度击穿63k(6.3万美刀)。[昨夜6.23内参说到了几个导致近期行情低迷的原因,比如,仅6月份以来,BTC矿工们就以一年来最快的速度,向市场倾泻了几十亿美刀的现货]。 其实,矿工慌…...

在 Vue 3 中设置 `@` 指向根目录的方法汇总
在 Vue 3 项目开发中,为了方便管理和引用文件路径,设置 指向根目录是一项常见的需求。以下为您总结了几种常见的实现方式。 方法一:使用 Vite 配置(适用于 Vite 构建的项目) 在项目根目录创建 vite.config.js 文件&a…...

基于 NXP LS1046 +FPGA系列 CPCI 架构轨道交通专用板卡
基于 NXP LS1046 系列 CPCI 架构轨道板卡 该产品是一款 CPCI 无风扇架构的高可靠性板卡,CPU 选用 NXP LS1046A 系统平台,支持嵌入式 Linux 或者标准 Ubuntu Linux 、凝思等操作系统,轨道交通 EMC 及宽温级别设计,板载多路 M12 高速…...

快速上手 Spring Boot:基础使用详解
快速上手 Spring Boot:基础使用详解 文章目录 快速上手 Spring Boot:基础使用详解1、什么是SpringBoot2、Springboot快速入门搭建3、SpringBoot起步依赖4、SpringBoot自动配置:以tomcat启动为例5、SpringBoot基础配置6、yaml7、多环境开发配置…...
react学习——08三点运算符
1、代码 let arr1[1,3,5,7,9]let arr2[2,4,6,8,10]console.log(...arr1);//展开一个数组let arr3[...arr1,...arr2]//连续数组//在函数中使用function sum (...numbers){console.log(,numbers)numbers.reduce((previousValue,currentValue)>{return previousValuecurrentVa…...

腾讯云OpenCloudOS系统上安装MySQL
在腾讯云OpenCloudOS系统上安装MySQL,可以通过以下步骤进行: 更新软件包列表: sudo yum update -y 安装MySQL服务器: sudo yum install mysql-server -y 启动MySQL服务: sudo systemctl start mysqld 设置MySQL…...

C++ - 介绍enum的使用
在 C 中,枚举关键字用于定义枚举,枚举是一种用户定义的数据类型,由一组命名的积分常量组成。枚举可以用有意义的名称来表示相关常量的集合,从而提高代码的可读性和可维护性。 In C, the enum keyword is used to define an enumer…...
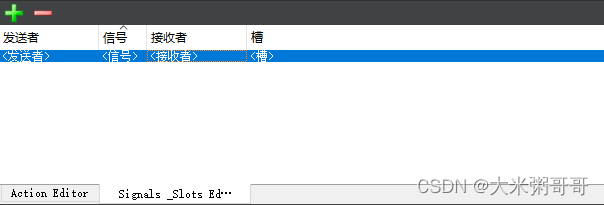
Qt 信号与槽的使用详解 - 多种绑定形式、同步异步、Lambda表达式等
Qt 信号与槽的使用详解 - 多种绑定形式、同步异步、Lambda表达式等 引言一、信号与槽常见的绑定形式二、信号与槽的连接方式 - 同步异步 引言 在Qt框架中,信号与槽(Signals and Slots)机制是一种强大的通信方式,它允许对象之间进…...

Appium+python自动化(十六)- ADB命令
简介 Android 调试桥(adb)是多种用途的工具,该工具可以帮助你你管理设备或模拟器 的状态。 adb ( Android Debug Bridge)是一个通用命令行工具,其允许您与模拟器实例或连接的 Android 设备进行通信。它可为各种设备操作提供便利,如安装和调试…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【JavaSE】多线程基础学习笔记
多线程基础 -线程相关概念 程序(Program) 是为完成特定任务、用某种语言编写的一组指令的集合简单的说:就是我们写的代码 进程 进程是指运行中的程序,比如我们使用QQ,就启动了一个进程,操作系统就会为该进程分配内存…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

Golang——6、指针和结构体
指针和结构体 1、指针1.1、指针地址和指针类型1.2、指针取值1.3、new和make 2、结构体2.1、type关键字的使用2.2、结构体的定义和初始化2.3、结构体方法和接收者2.4、给任意类型添加方法2.5、结构体的匿名字段2.6、嵌套结构体2.7、嵌套匿名结构体2.8、结构体的继承 3、结构体与…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...
