线性代数、矩阵计算

一、线性代数

1、对于向量，若a是标量，为a的绝对值乘以b的向量长度。

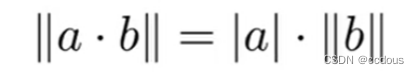
2、点乘

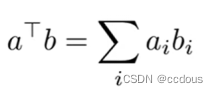
3、范数：向量或者矩阵的长度

        L1范数：（对向量）每个元素的绝对值求和

        L2范数：（对向量）torch.norm(向量)，得到一个标量，元素平方和的开根

        F范数：（对矩阵）第4点中

4、范数，b、c为向量，A为矩阵。矩阵范数有点复杂，我们一般用F范数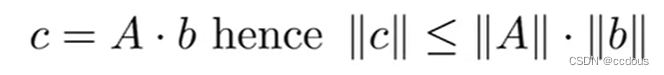

        （1）矩阵范数：最小满足上面公式的值

        （2）F范数：就像拉长了一样

                

5、对称和反对称，定义跟线代不太一样，反对称是另一半为负对称

6、正定矩阵：这个矩阵这样乘以任何一个向量都大于等于0

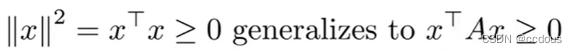
7、正交矩阵

8、置换矩阵（是正交矩阵，每行每列只有一个为1，线代里面我们用于做初等变化）

9、特征值与特征向量

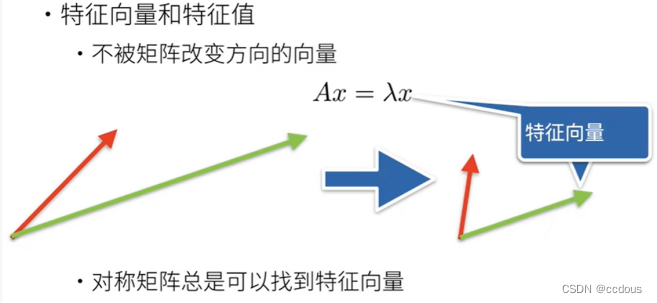
二、Pytorch中的线代

1、只有一个元素的张量是标量

2、求和，可以选择轴，降低维度相当于在那个轴上拍扁。

        （1）eg: A.shape->torch.Size([2,5,4])

        

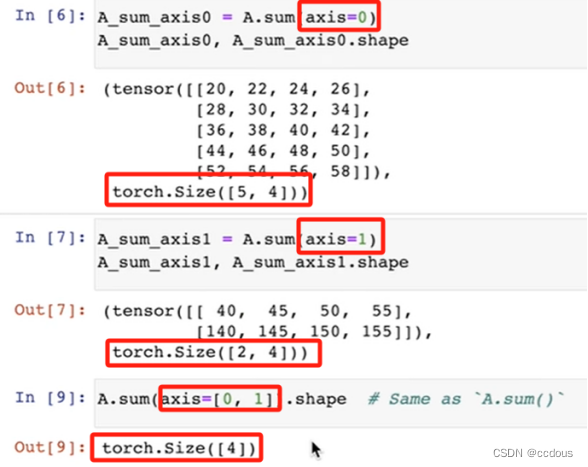
        （2）使用keepdims可以保留维度，便于广播机制同样shape操作，被求和那个维度大小变为1，也就是前者直接拍扁了，后者会按的长度为1

        

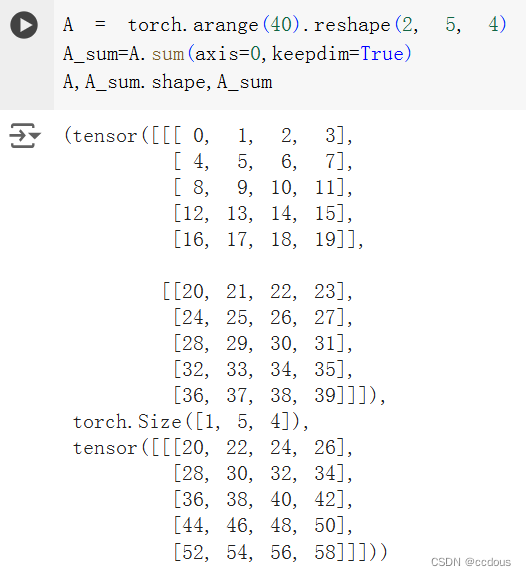
3、求均值A.mean()或A.average()，等价于求和除以元素个数（也可以定维度计算）

此处A.shape[]可得出该维度的长度

4、累加求和A.cumsum(axis=n)：每个位置是他前面的元素的和

        

5、矩阵乘以向量mv=Matrix Vector Multiplication，矩阵乘以矩阵mm

        

6、求L2范数torch.norm(向量)，得到一个标量；求L1范数每个元素的绝对值求和；对矩阵，F范数，前面写到了，torch.norm(矩阵)。

三、矩阵计算

1、亚导数（应用于不可微的函数），比如绝对值函数

        

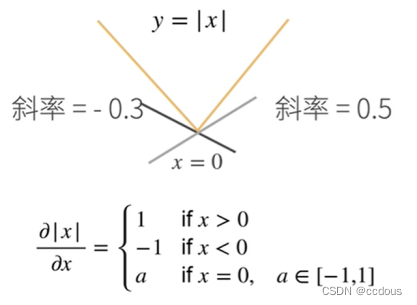
2、将导数扩展到向量则为梯度，表示变化最大的那个方向

        （1）Y是标量，x是列向量，y关于x求导是行矩阵

                

                

        （2）Y是列向量，x是标量，y关于x求导也是列矩阵

                

        （3）向量关于向量求导是矩阵

                

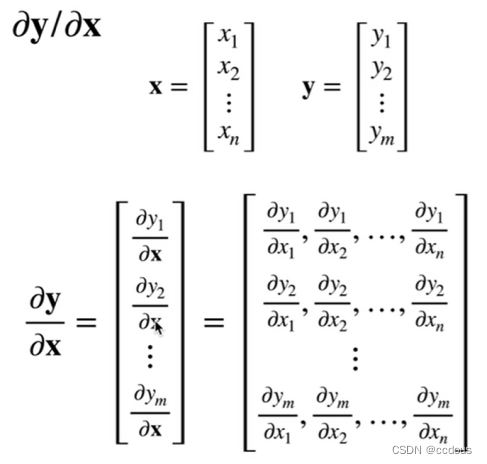
                I是对角矩阵，a是与x无关的矩阵

                

                下图中后面部分求导，相当于把下部的向量转置

                

                                                                                                        对不起，李沐老师