树与二叉树(概念篇)
树与二叉树
- 1 树的概念
- 1.1 树的简单概念
- 1.2 树的概念名词
- 1.3 树的相关表示
- 2 二叉树的概念
- 2.1 二叉树的简单概念
- 2.1.1 特殊二叉树
- 2.2 二叉树的性质
- 2.3 二叉树的存储结构
1 树的概念
1.1 树的简单概念
树是一种非线性的数据结构,它是由n(n>=0)个有限节点组成的一个具有层次关系的集合。把它称作树是因为它看起来就像一棵倒挂的树,也就是说它的根在上,而叶在下。
- 树有一个特殊的节点,称为根节点,根节点没有前驱节点。
- 除根节点外,其余节点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<=i<=m)又是一棵结构与树类似的子树。这样的每棵子树的根节点有且只有一个前驱,可以有0个或多个后继节点。
- 由此可见,树是递归定义的。
注意:树形结构中,子树之间不能有交集(不能成环),否则就不是树形结构。
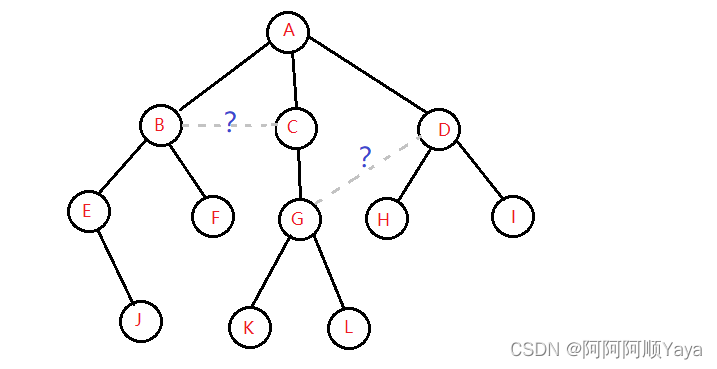
除了根节点外,每个节点有且只有一个父节点,所以可以得出:一棵N个节点的树有N-1条边。
1.2 树的概念名词
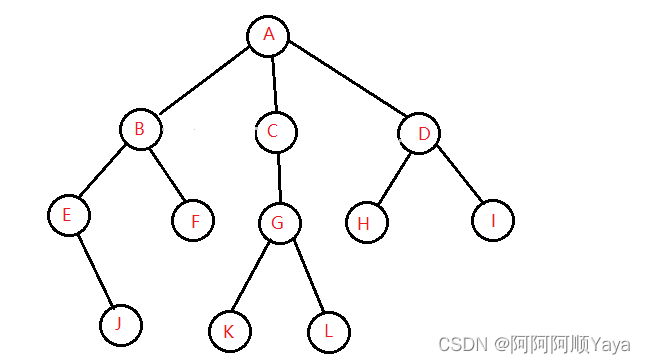
节点的度:一个节点含有的子树的个数称为该节点的度。如图:A节点的度为3。
叶节点或终端节点:度为0的节点称为叶节点。如图:J、F、K、L、H、I都是叶节点。
非终端节点或分支节点:度不为0的节点。
双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点。如图:A分别是B、C、D的父节点。
孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点。如图:B、C、D都是A的子节点。
兄弟节点:具有相同父节点的节点互称为兄弟节点。
树的度:一棵树中,最大的节点的度称为树的度。
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,依此类推。
树的高度或深度:树中节点的最大层次。如图:树的高度为4。
堂兄弟节点:双亲在同一层的节点互为堂兄弟节点。
节点的祖先:从根到该节点所经分支上的所有节点。如图:A节点是所有节点的祖先。
子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如图:所有节点都是A节点的子孙。
森林:由m(m>0)棵互不相交的树组成的集合称为森林。
1.3 树的相关表示
树形结构相对线性结构就比较复杂了,要存储表示起来也就比较麻烦了。既要保存值域,也要保存节点和节点之间的关系。实际中树有很多种表示方式,如:双亲表示法,孩子表示法,孩子双亲表示法以及孩子兄弟表示法等。但最常用的还是孩子兄弟表示法。
可将上图中树的结构用孩子兄弟表示法转化,如下图所示:
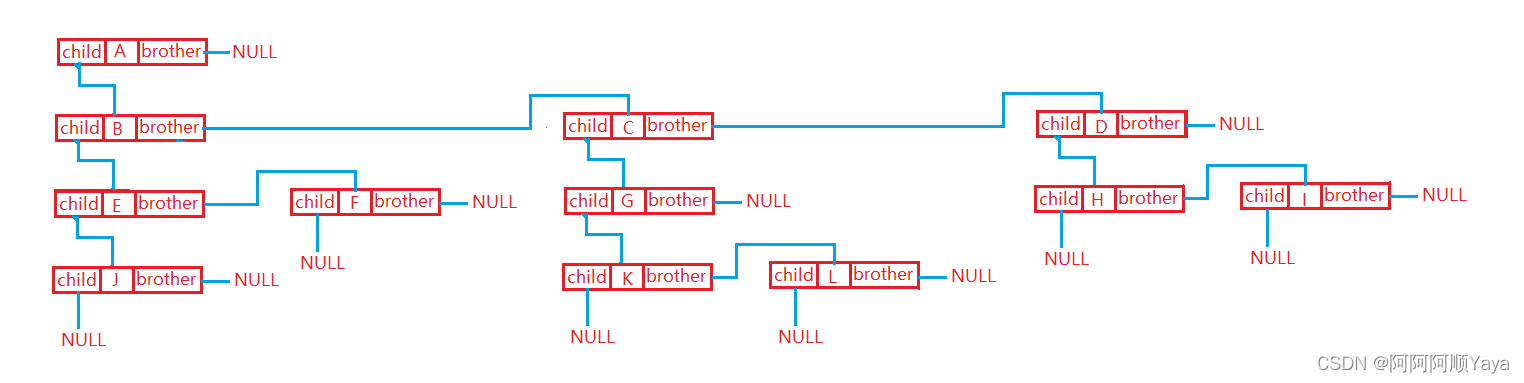
孩子兄弟表示法是用于将任意一棵普通的树转化为二叉树的最有效方法,其节点的结构定义大致如下:
typedef int DataType;
struct Node
{struct Node* _pfirstChild; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};
2 二叉树的概念
2.1 二叉树的简单概念
一棵二叉树是节点的一个有限集合,该集合:
- 或者为空
- 或者由一个根节点加上两棵别称为左子树和右子树的二叉树组成
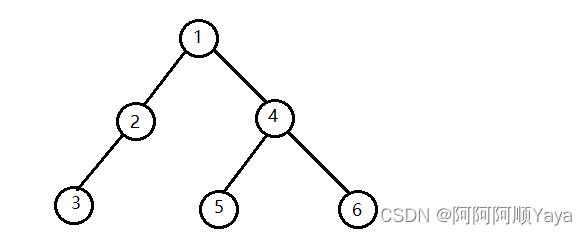
从上图可以看出:
- 二叉树不存在度大于2的节点
二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树
所以可得出,对于任意的二叉树都是由以下几种情况组合构成的:
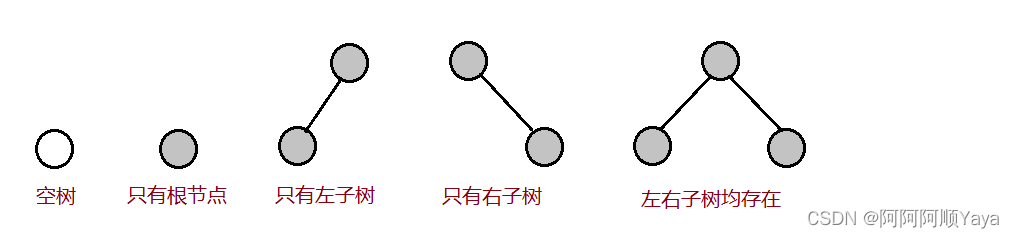
2.1.1 特殊二叉树
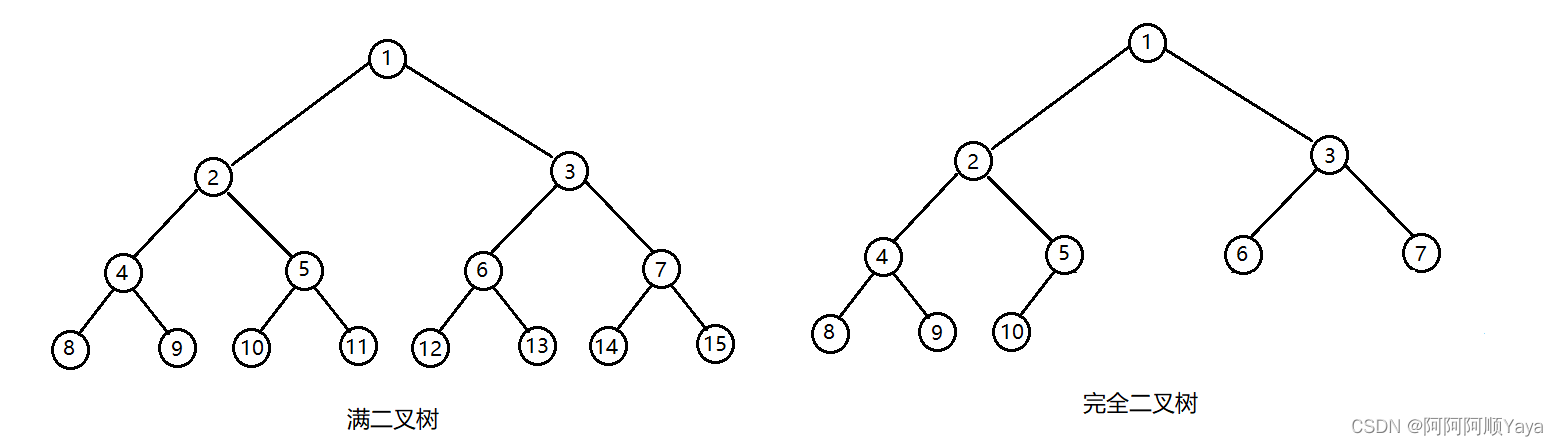
- 满二叉树:一个二叉树,如果每一层的节点数都达到最大值,则这个二叉树就叫做满二叉树。也就是说,如果一棵树的高度为h,且节点总数为2h−12^h-12h−1,则它就是满二叉树。
- 完全二叉树:完全二叉树是一种效率很高的数据结构。完全二叉树是由满二叉树引出来的。对于高度为h的,有n个节点的树,当且仅当其每一个节点都与高度为h的满二叉树中编号从1至n的节点都一一对应时,才被称之为完全二叉树。要注意的是满二叉树是一种特殊的完全二叉树。
2.2 二叉树的性质
- 若规定根节点的层数为1,则一棵非空二叉树的第i层上最多有2(i−1)2^{(i-1)}2(i−1)个节点。
- 若规定根节点的层数为1,则高度为h的二叉树的最大节点数是2h−12^h-12h−1。
- 对于任意一棵二叉树,如果度为0的叶节点个数是n0n_0n0,度为2的分支结点个数是n2n_2n2,则有n0=n2+1n_0=n_2+1n0=n2+1。
- 若规定根节点的层数是1,则具有n个节点的满二叉树的高度:h=log2(n+1)h=log_2(n+1)h=log2(n+1)。
- 对于具有n个节点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的节点有:
若i>0,i节点位置的双亲序号为:(i-1)/2;若i=0,i为根结点序号,无双亲节点。
若2*i+1<n,则 i 节点位置的左孩子序号为:2*i+1(2*i+1>=n时无左孩子)
若2*i+2<n,则 i 节点位置的右孩子序号为:2*i+2(2*i+2>=n时无右孩子)
2.3 二叉树的存储结构
二叉树一般可以使用两种结构进行存储,一种是顺序结构,一种是链式结构。
- 顺序结构存储
顺序结构存储就是使用数组来存储。但数组存储一般只适合表示完全二叉树,因为不是完全二叉树会有空间的浪费。实际使用中只有堆(属于完全二叉树)才会使用数组来存储。二叉树顺序存储在物理上是一个数组,在逻辑上是一棵二叉树。 - 链式结构存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示节点间的逻辑关系。通常的方法是链表中的每个节点由三个域组成:数据域和左右指针域。左右指针分别用来存放该节点左孩子和右孩子所在的链节点的地址。链式结构又分为二叉链和三叉链。简单的一般二叉链就够了,更复杂的数据结构如红黑树等会用到三叉链。
相关文章:

树与二叉树(概念篇)
树与二叉树1 树的概念1.1 树的简单概念1.2 树的概念名词1.3 树的相关表示2 二叉树的概念2.1 二叉树的简单概念2.1.1 特殊二叉树2.2 二叉树的性质2.3 二叉树的存储结构1 树的概念 1.1 树的简单概念 树是一种非线性的数据结构,它是由n(n>0)个有限节点组成的一个具…...
C++回顾(二十五)—— map/multimap容器
25.1 map/multimap的简介 map是标准的关联式容器,一个map是一个键值对序列,即(key,value)对。它提供基于key的快速检索能力。map中key值是唯一的。集合中的元素按一定的顺序排列。元素插入过程是按排序规则插入,所以不能指定插入位置。map的…...

7.3 向量的数量积与向量积
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

Qt静态扫描(命令行操作)
Qt静态扫描(命令行操作) 前沿: 静态代码分析是指无需运行被测代码,通过词法分析、语法分析、控制流、数据流分析等技术对程序代码进行扫描,找出代码隐藏的错误和缺陷,如参数不匹配,有歧义的嵌…...

【Hadoop】配置文件
Hadoop 配置文件分两类:默认配置文件和自定义配置文件,只有用户想修改某一默认 配置值时,才需要修改自定义配置文件,更改相应属性值 (1)默认配置文件: cd $HADOOP_HOME/share/hadoop common路…...

python进程池
Python进程池是Python标准库中multiprocessing模块提供的一种用于管理进程的方式。它可以使Python程序以并行的方式执行任务,提高程序的运行效率。本篇博客将介绍如何使用Python进程池。 创建进程池 在使用Python进程池之前,我们需要先创建一个进程池对…...
笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据
如果笔记本固态盘数据丢失怎么办?笔记本固态盘怎么恢复数据?下面将为大家详细地介绍一下笔记本固态硬盘数据恢复的三种实用方法,希望对大家有所帮助。一、简单恢复方法笔记本固态硬盘数据删除以后,较为简单直接的恢复方法就是从回…...
堆的结构与实现
堆的结构与实现二叉树的顺序结构堆的概念及结构堆的实现堆的创建向上调整建堆向下调整建堆堆的操作链接二叉树的顺序结构 堆其实是具有一定规则限制的完全二叉树。 普通的二叉树是不太适合用数组来存储的,因为可能会存在大量的空间浪费。而完全二叉树会更适合使用顺…...

Pandas快速入门
Pandas是Python中非常流行的数据处理库之一,它提供了一种简单而强大的方法来处理和分析数据。在本篇文章中,我将向你介绍Pandas的基础知识,以便你可以开始使用它来处理和分析数据。 安装Pandas 首先,你需要安装Pandas。可以通过…...
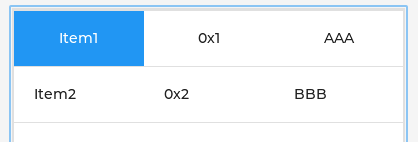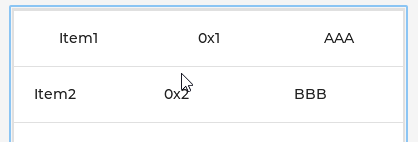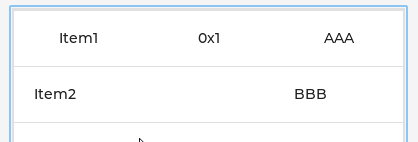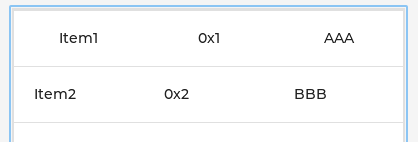
LVGL学习笔记18 - 表Table
目录 1. Parts 1.1 LV_PART_MAIN 1.2 LV_PART_ITEMS 2. 样式 2.1 设置行列数 2.2 设置单元格字符串 2.3 设置单元格宽度 2.4 设置表格高度和宽度 2.5 设置字符串颜色 2.6 设置边框颜色 2.7 设置背景颜色 3. 事件 4. CELL CTRL 表格是由包含文本的行、列和单元格构…...

嵌入式安防监控项目——html框架分析和环境信息刷新到网页
目录 一、html控制LED 二、模拟数据上传到html 一、html控制LED 简单来说就是html给boa服务器发了一个控制指令信息,然后boa转发给cgi进程,cgi通过消息队列和主进程通信。主进程再去启动LED子线程。 这是老师给的工程。 以前学32都有这工具那工具来管…...
centos安装docker详细步骤
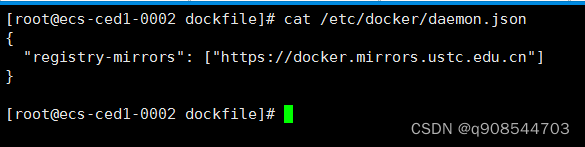
目录 一.前言 1.环境要求2.官网中文安装参考手册 二.安装步骤 1.卸载旧版本2.安装需要的软件包3.设置docker镜像源 1.配置docker镜像源 方式1:官网地址(外国):方式2:阿里云源:2.查看配置是否成功 4.更新yum软件包索引5.可以查看…...
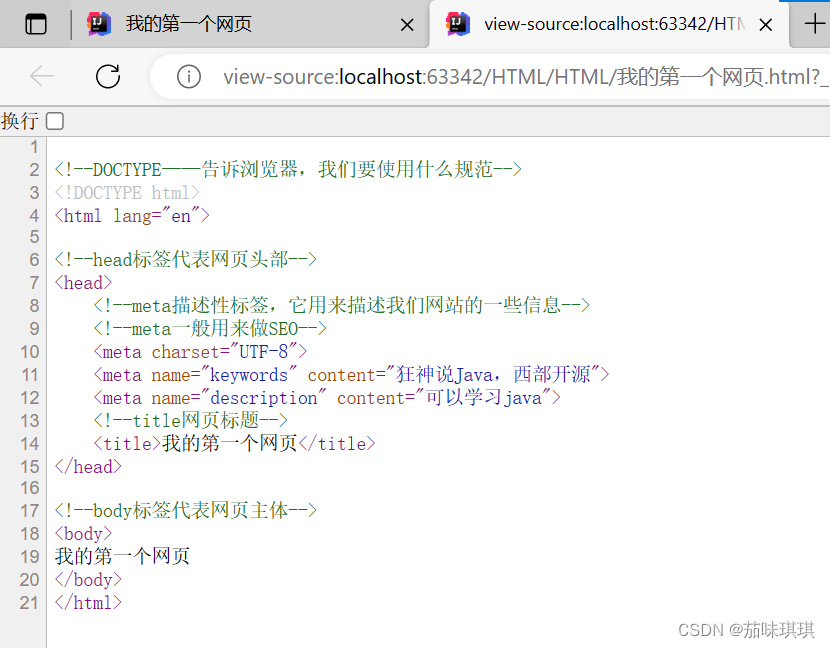
初识HTML、W3C标准、如何利用IDEA创建HTML项目、HTML基本结构、网页基本信息
一、什么是HTML? HTML——Hyper Text Markup Languagr(超文本标记语言) 超文本包括:文字、图片、音频、视频、动画等 目前网页中常用——HTML5 HTML5提供了一些新的元素和一些有趣的新特性,同时也建立了一些新的规则…...

为什么程序员喜欢这些键盘?
文章目录程序员的爱介绍个人体验程序员的爱 程序员是长时间使用计算机的群体,他们需要一款高品质的键盘来保证舒适的打字体验和提高工作效率。在键盘市场上,有很多不同类型的键盘,但是对于程序员来说,机械键盘是他们最钟爱的选择…...

JS中数组去重的几种方法
JS 中有多种方法可以实现数组去重,下面是几种常用的方法:1、使用 Set 去重:Set 数据结构中不能有重复元素,可以将数组转成 Set 类型,再转回数组。let arr [1,2,3,4,5,6,2,3,4]; let uniqueArr [...new Set(arr)]; co…...

Nginx 配置实例-负载均衡
一、实现效果 浏览器地址栏输入地址 http://192.168.137.129/edu/a.html,负载均衡效果,将请求平均分配到8080和8081两台服务器上。 二、准备工作 1. 准备两台tomcat服务器,一台8080,一台8081 (具体操作如下两个链接) Nginx配置实…...

引出生命周期、生命周期_挂载流程、生命周期_更新流程、生命周期_销毁流程、生命周期_总结——Vue
目录 一、引出生命周期 二、生命周期_挂载流程 三、生命周期_更新流程 四、生命周期_销毁流程 五、生命周期_总结 一、引出生命周期 生命周期: 1.又名:生命周期回调函数、生命周期函数、生命周期钩子。 2.是什么:Vue在关键时刻帮我们调…...

C++ STL学习之【vector的使用】
✨个人主页: Yohifo 🎉所属专栏: C修行之路 🎊每篇一句: 图片来源 The power of imagination makes us infinite. 想象力的力量使我们无限。 文章目录📘前言📘正文1、默认成员函数1.1、默认构造…...

方差分析与单因素方差分析
研究分类型自变量对数值型因变量的影响。检验统计的设定和检验方法与变量间的方差是否相等有关。 例如研究行业、服务等级对投诉数的影响:如表格中给出4个行业、每个行业有3个服务等级、样本容量为7、观测值为投诉数。则构成一个3维的矩阵。 在上述基础上…...

分布式链路追踪组件skywalking介绍
SkyWalking组件概念 一个开源的可观测平台, 用于从服务和云原生基础设施收集, 分析, 聚合及可视化数据。SkyWalking 提供了一种简便的方式来清晰地观测分布式系统, 甚至横跨多个云平台。SkyWalking 更是一个现代化的应用程序性能监控(Application Performance Monitoring)系统…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

【Redis技术进阶之路】「原理分析系列开篇」分析客户端和服务端网络诵信交互实现(服务端执行命令请求的过程 - 初始化服务器)
服务端执行命令请求的过程 【专栏简介】【技术大纲】【专栏目标】【目标人群】1. Redis爱好者与社区成员2. 后端开发和系统架构师3. 计算机专业的本科生及研究生 初始化服务器1. 初始化服务器状态结构初始化RedisServer变量 2. 加载相关系统配置和用户配置参数定制化配置参数案…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
