群体优化算法---石墨烯优化算法介绍以及在期权定价上的应用(Black-Scholes模型来计算欧式期权的理论价格)
介绍
石墨烯算法是一种新兴的优化算法,灵感来自于石墨烯的结构和特性。石墨烯是一种由碳原子构成的二维蜂窝状晶格结构,具有优异的机械、电学和热学性能。石墨烯算法通过模拟石墨烯原子之间的相互作用和迁移,来求解复杂的优化问题
基本概念
石墨烯的结构:
石墨烯由碳原子组成,每个碳原子与其他三个碳原子通过共价键连接,形成一个蜂窝状的二维晶格结构。这种结构使得石墨烯具有非常高的强度和导电性。
石墨烯算法的灵感:
石墨烯算法借鉴了石墨烯的这种晶格结构和原子迁移特性,通过模拟碳原子在二维平面上的移动和相互作用,来寻找优化问题的最优解
算法步骤
初始化:
初始化一组解,称为“碳原子”,并将它们随机分布在二维平面上。这些解代表了问题的初始解集。
评估适应度:
计算每个碳原子的适应度值,根据适应度函数评估每个解的优劣。
更新位置:
根据某种规则更新碳原子的位置,模拟碳原子在二维平面上的迁移。这种迁移可以通过模拟退火、粒子群算法或其他元启发式方法来实现。
局部搜索:
在每次迭代中,对每个碳原子进行局部搜索,进一步优化其位置。局部搜索可以通过梯度下降或其他局部优化方法来实现。
选择与替换:
根据适应度值选择较优的碳原子,并用它们替换较差的碳原子,形成新的解集。
迭代:
重复上述步骤,直到达到预定的迭代次数或满足收敛条件。
石墨烯算法的优点
全局搜索能力强:
石墨烯算法能够在广阔的搜索空间中找到全局最优解,避免陷入局部最优。
收敛速度快:
通过模拟碳原子的快速迁移和局部优化,石墨烯算法具有较快的收敛速度。
适应性强:
石墨烯算法可以处理各种类型的优化问题,包括连续、离散和混合优化问题
石墨烯算法的应用
石墨烯算法可以应用于许多实际问题,如:
工程优化:
用于结构优化、路径规划、资源分配等工程领域的问题。
机器学习:
用于神经网络训练、特征选择、超参数优化等机器学习任务。
数据挖掘:
用于聚类分析、关联规则挖掘、分类等数据挖掘任务。
金融优化:
用于投资组合优化、风险管理、期权定价等金融领域的问题
本文代码
定义期权定价模型:我们可以使用Black-Scholes模型来计算欧式期权的理论价格。
设计石墨烯优化算法:模拟石墨烯原子之间的相互作用和迁移,以找到最优的期权定价参数。
整合并实现:将期权定价模型和石墨烯算法整合在一起。
期权定价模型(Black-Scholes)
Black-Scholes模型用于计算欧式看涨期权(Call Option)和看跌期权(Put Option)的价格:
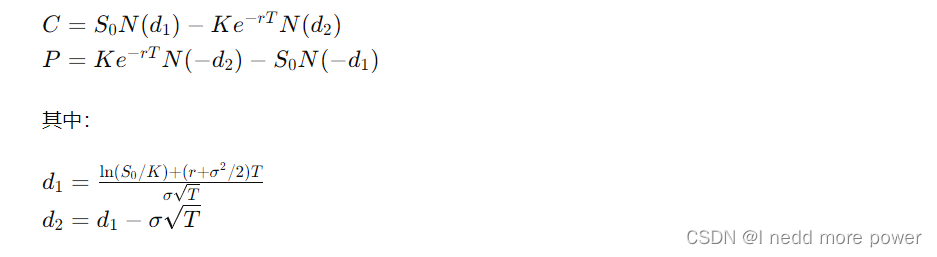
核心代码
Graphene_Option_Pricing.m
function [best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call)% 参数初始化dim = 1; % 需要优化的参数维度:波动率σlower_bound = [0.01]; % 下界:波动率upper_bound = [1.0]; % 上界:波动率max_iter = 500; % 最大迭代次数pop_size = 30; % 种群大小% 适应度函数:计算Black-Scholes理论价格与市场价格的均方误差fitness_func = @(params) calculate_fitness(params, S0, K, r, T, market_price, is_call);% 石墨烯优化算法[best_params, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func);disp('Best parameters found:');disp(best_params);disp('Fitness of best parameters:');disp(best_fitness);% 验证找到的最佳波动率参数optimal_sigma = best_params(1);% 使用最佳波动率参数计算期权价格if is_callmodel_price = Black_Scholes_Call(S0, K, r, optimal_sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, optimal_sigma, T);end% 打印模型价格和市场价格进行比较disp('Optimal sigma:');disp(optimal_sigma);disp('Model option price with optimal sigma:');disp(model_price);disp('Market option price:');disp(market_price);
endfunction fitness = calculate_fitness(params, S0, K, r, T, market_price, is_call)sigma = params(1);if is_callmodel_price = Black_Scholes_Call(S0, K, r, sigma, T);elsemodel_price = Black_Scholes_Put(S0, K, r, sigma, T);end
endfunction C = Black_Scholes_Call(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);C = S0 * normcdf(d1) - K * exp(-r * T) * normcdf(d2);
endfunction P = Black_Scholes_Put(S0, K, r, sigma, T)d1 = (log(S0 / K) + (r + 0.5 * sigma^2) * T) / (sigma * sqrt(T));d2 = d1 - sigma * sqrt(T);P = K * exp(-r * T) * normcdf(-d2) - S0 * normcdf(-d1);
endfunction [best_solution, best_fitness] = Graphene_Optimization(dim, lower_bound, upper_bound, max_iter, pop_size, fitness_func)% 初始化positions = lower_bound + (upper_bound - lower_bound) .* rand(pop_size, dim);% 主循环for iter = 1:max_iter% 更新位置for i = 1:pop_size% 模拟碳原子的迁移new_position = positions(i, :) + rand(1, dim) .* (best_solution - positions(i, :));new_position = max(min(new_position, upper_bound), lower_bound);new_fitness = fitness_func(new_position);% 局部搜索if new_fitness < fitness(i)positions(i, :) = new_position;fitness(i) = new_fitness;end% 更新最优解if new_fitness < best_fitnessbest_fitness = new_fitness;best_solution = new_position;endend% 记录迭代过程中的最优值(可选)disp(['Iteration ', num2str(iter), ': Best Fitness = ', num2str(best_fitness)]);end
endrun_graphene_option_pricing.m
function run_graphene_option_pricing% 示例使用
S0 = 100; % 当前股票价格
K = 100; % 执行价格
r = 0.05; % 无风险利率
T = 1; % 到期时间(年)
market_price = 10; % 市场期权价格
is_call = true; % 是否为看涨期权[best_params, best_fitness] = Graphene_Option_Pricing(S0, K, r, T, market_price, is_call);
disp('Best parameters for sigma:');
disp(best_params);
disp('Best fitness:');
disp(best_fitness);end
说明
初始化:初始化石墨烯算法的种群,包括参数的上下界、最大迭代次数和种群大小。
适应度函数:计算理论价格和市场价格之间的均方误差。
Black-Scholes模型:计算欧式看涨期权和看跌期权的价格。
石墨烯优化算法:通过模拟石墨烯原子的迁移和相互作用,找到最佳的期权定价参数。
结果输出:输出最佳参数和相应的适应度值。
效果
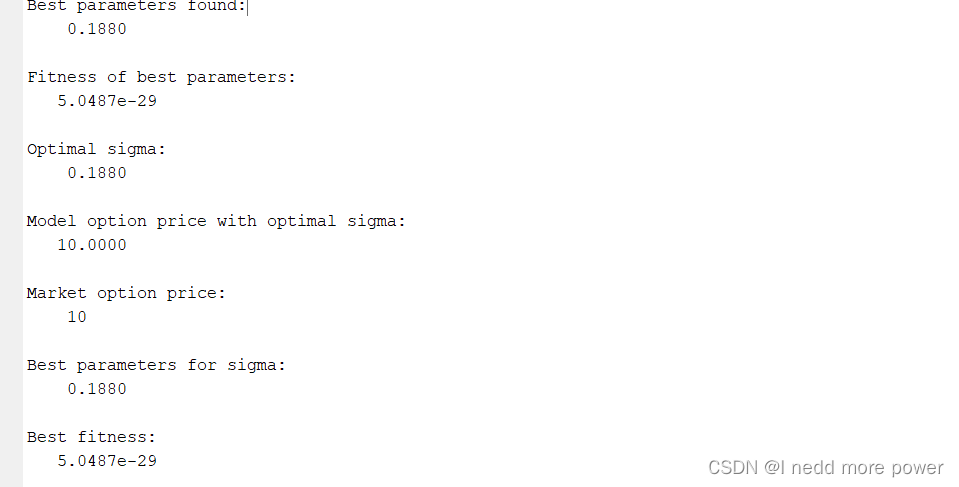
完整代码获取
微信扫一扫,回复"石墨烯优化算法"即可查看完整代码

相关文章:

群体优化算法---石墨烯优化算法介绍以及在期权定价上的应用(Black-Scholes模型来计算欧式期权的理论价格)
介绍 石墨烯算法是一种新兴的优化算法,灵感来自于石墨烯的结构和特性。石墨烯是一种由碳原子构成的二维蜂窝状晶格结构,具有优异的机械、电学和热学性能。石墨烯算法通过模拟石墨烯原子之间的相互作用和迁移,来求解复杂的优化问题 基本概念…...

创纪录!沃飞长空完成新一轮融资,实力获资方认可
作为全球竞逐的战略性新兴产业,今年首次写入政府工作报告的“低空经济”热度正持续提升,在政策、产业等多个层面均有重大突破。行业的飞速发展也吸引了投资界的目光,越来越多资本正投向低空经济。 近期,国内领先的低空出行企业吉…...
1991java Web体检预约管理系统eclipse定制开发mysql数据库BS模式java编程jdbc
一、源码特点 JSP体检预约管理系统是一套完善的web设计系统,对理解JSP java 编程开发语言有帮助,系统具有完整的源代码和数据库,系统主要采用B/S模式开发。开发环境为TOMCAT7.0,eclipse开发,数据库为Mysql5.0,使用…...

如何优雅终止线程/线程池
如何优雅终止线程 分为两个阶段终止线程 1、interrupted(): 让线程从休眠状态转换到RUNNABLE 状态 2、线程终止的标志位:线程会在合适的时机检查这个标志位,如果发现符合终止条件,则自动退出 run() 方法 public class MonitorThread extends Thread {/…...
泰迪智能科技实验室产品-云计算资源管理平台介绍
云计算资源管理平台是一款集群应用程序管理平台,以Docker、Kubernetes为核心引擎的容器化应用部署、运行环境,对数据中心的物理服务器、网络、存储、虚拟服务器等基础架构资源进行集中统一的管理、分配、监控等。平台旨在围绕行业应用逐步由“虚拟化”向…...

.Net WebApi启动 Swagger异常报错: Failed to load API definition
问题描述: 基于.Net6.0的WebApi 启动Swagger报错:Failed to load API definition。即无法加载API定义。 解决方法: 分析程序输出日志: 错误信息: ERROR Microsoft.AspNetCore.Diagnostics.DeveloperExceptionPageMid…...
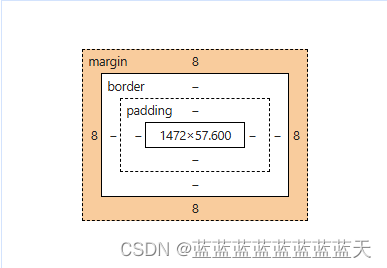
CSS新手入门笔记【导入方法、选择器介绍、选择器优先级、属性详细介绍、盒子模型】
目录 一、目的与优势二、CSS导入方式三、语法结构四、选择器类型基本选择器组合选择器伪类与伪元素属性选择器 六、选择器优先级总结 六、CSS属性1. 字体与文本属性2. 背景属性3. 尺寸与盒模型属性4. 布局与定位5. 列表样式6. 边框与轮廓7. 文本装饰与效果8. 动画与过渡9. 伪类…...

制作高校专属PPT时,如何将校徽设置成透明底色?无须PS
目录 示例:以清华大学为例 1必应搜索“清华大学校徽” 2保存清华大学校徽及校名。 3将校徽导入到PPT中 4 选中校徽,然后依次选择“图片格式”-->颜色-->设置透明色编辑 5出现“画笔”,由于截图的缘故,画笔没有在截…...

设计模式之【适配器模式】
类适配器实现(继承) 类适配器通过继承来实现适配器功能 // 目标接口 public interface Target {void request(); }// 被适配者 public class Adaptee {public void specificRequest() {System.out.println("Adaptee: specificRequest");} }/…...
AI论文降重:一键操作,让你的论文查重率瞬间下降
高查重率是许多毕业生的困扰。通常,高查重率源于过度引用未经修改的参考资料和格式错误。传统的降重方法,如修改文本和增添原创内容,虽必要但耗时且成效不一。 鉴于此,应用AI工具进行AIGC降重成为了一个高效的解决方案。这些工具…...

Cmake--学习笔记
🚀write in front🚀 🔎大家好,我是黄桃罐头,希望你看完之后,能对你有所帮助,不足请指正!共同学习交流 🎁欢迎各位→点赞👍 收藏⭐️ 留言📝…...

LangChain让LLM带上记忆
最近两年,我们见识了“百模大战”,领略到了大型语言模型(LLM)的风采,但它们也存在一个显著的缺陷:没有记忆。 在对话中,无法记住上下文的 LLM 常常会让用户感到困扰。本文探讨如何利用 LangCha…...
Word恢复历史文档,记好4个方法就足够
“我正在准备一个重要的报告,但是电脑突然就崩溃了,导致我的文档还没保存就被关闭了,大家有什么方法可以恢复Word历史文档吗?快给我出出主意吧!” 在数字化时代,文档编辑和保存已经成为我们日常工作和学习中…...
收银系统源码-千呼新零售2.0【线上营销】
千呼新零售2.0系统是零售行业连锁店一体化收银系统,包括线下收银线上商城连锁店管理ERP管理商品管理供应商管理会员营销等功能为一体,线上线下数据全部打通。 适用于商超、便利店、水果、生鲜、母婴、服装、零食、百货等连锁店使用。 详细介绍请查看&a…...

OnlyOffice测评
官方链接: https://www.onlyoffice.com/zh/office-suite.aspx https://www.onlyoffice.com/zh/pdf-editor.aspx OnlyOffice:引领办公效率的新标杆 在数字化时代的浪潮中,办公软件已经成为我们日常工作中不可或缺的一部分。然而,…...

UDS - 8 Application layer protocol
8 应用层协议 来自:ISO 14229-1-2020.pdf 8.1 一般定义 应用层协议应始终是确认消息传输,这意味着对于从客户端发送的每个服务请求,服务器应发送一个或多个相应的响应。 此规则的唯一例外是使用功能寻址或请求/指示指定不生成响应/确认的少数情况。为了不给系统带来许多不…...

二叉树公共最近祖先
文章目录 1. **二叉搜索树(Binary Search Tree, BST)**2. **一般二叉树****递归方法**:**迭代方法**: 案例展示二叉搜索树(BST)中查找LCA一般二叉树中查找LCA1. **使用哈希表存储父节点信息**2. **处理多个查询**3. **异常处理**结…...

智慧运维系统指导规范
随着信息技术的迅猛发展,智慧运维系统在现代企业中扮演着越来越重要的角色。为了提高运维效率、保障系统稳定运行,并制定一套科学、合理的智慧运维系统指导规范至关重要。本规范旨在为企业提供一套全面、系统的智慧运维管理方法和操作准则,以…...

最新自助下单彩虹云商城系统源码,含小储云商城模板免授权
最新彩虹商城源码,含小储云商城模板免授权,试用了一下还行,具体的大家可以看看 源码下载:https://download.csdn.net/download/m0_66047725/89405387 更多资源下载:关注我。...

头条系统-05-延迟队列精准发布文章-概述添加任务(db和redis实现延迟任务)、取消拉取任务定时刷新(redis管道、分布式锁setNx)
文章目录 延迟任务精准发布文章1)文章定时发布2)延迟任务概述2.1)什么是延迟任务2.2)技术对比2.2.1)DelayQueue2.2.2)RabbitMQ实现延迟任务2.2.3)redis实现 3)redis实现延迟任务4)延迟任务服务实现4.1)搭建heima-leadnews-schedule模块4.2)数据库准备4.3)安装redis4.4)项目集成…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

从WWDC看苹果产品发展的规律
WWDC 是苹果公司一年一度面向全球开发者的盛会,其主题演讲展现了苹果在产品设计、技术路线、用户体验和生态系统构建上的核心理念与演进脉络。我们借助 ChatGPT Deep Research 工具,对过去十年 WWDC 主题演讲内容进行了系统化分析,形成了这份…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

微信小程序云开发平台MySQL的连接方式
注:微信小程序云开发平台指的是腾讯云开发 先给结论:微信小程序云开发平台的MySQL,无法通过获取数据库连接信息的方式进行连接,连接只能通过云开发的SDK连接,具体要参考官方文档: 为什么? 因为…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...
