B+树与索引解析
文章目录
- B+树与索引简介
- 几个关键点
- 应用案例
- 场景描述
- 索引创建
- 查询操作
- 更新操作
- 并发处理
- Python代码示例
B+树与索引简介
B+树是一种在计算机科学中广泛使用的自平衡的树数据结构,它能保持数据排序,并且搜索、插入和删除操作的时间复杂度都是O(log n)。B+树被广泛用于数据库和文件系统中,特别是在实现索引时。
在B+树中,所有的值都存储在叶子节点中,而内部节点只用于导航。每个节点可以有多个子节点,这使得B+树的高度相对较低,从而减少了磁盘I/O次数,提高了效率。每个节点包含一个键值对列表,键值对按照键的顺序排序。每个内部节点还包含指向其子节点的指针列表,这些指针指向子节点中的第一个键值对。
在数据库中,B+树通常用于实现索引。当创建一个索引时,数据库会在表中创建一个B+树结构,其中的键是索引列的值,而值是指向实际数据行的指针。这样,当需要查询数据时,可以通过B+树快速地找到所需的数据行,而无需扫描整个表。由于B+树的高度相对较低,因此查询速度非常快,即使在大型数据库中也是如此。
总之,B+树是一种高效的数据结构,适用于大量数据的排序和搜索。在数据库中,B+树通常用于实现索引,以提高查询速度和性能。
几个关键点
当我们更深入地讨论B+树和索引的关系时,有几个关键点需要注意:
-
叶子节点链接:在B+树中,所有叶子节点通过指针相互链接,形成一个链表。这意味着,如果查询的范围跨越多个键值,如在一个区间内查找数据,那么只需要沿着这个链表进行线性扫描,而不需要重新访问根节点或进行深度优先搜索。这对于范围查询特别有用,比如SQL中的
BETWEEN语句。 -
多级索引:在大型数据库中,单层的B+树可能不足以处理巨大的数据量。因此,数据库可能会使用多级索引来进一步优化性能。例如,第一级索引可能是一个B+树,其中的键值是主键的一部分,而值是指向第二级索引的指针。第二级索引可能是一个哈希表或其他类型的索引,用于快速定位具体的行。这种多级索引结构可以在保持高查询速度的同时,处理非常大的数据集。
-
更新操作:虽然B+树在查询方面表现优异,但在频繁的更新操作(插入、删除)下,它需要进行分裂和合并操作来保持平衡,这会消耗更多的资源。因此,在设计数据库系统时,需要权衡索引的读写性能。
-
空间利用率:B+树的设计允许每个节点存储多个键值对,这提高了磁盘空间的利用率,因为每个磁盘I/O操作可以处理更多数据。在现代数据库系统中,这尤为重要,因为它可以减少昂贵的磁盘I/O操作次数。
-
并发控制:在多用户环境中,数据库必须能够处理并发的读写操作。B+树的结构允许对不同节点进行锁定,以支持并发控制机制,如行级锁或页级锁,从而在保证数据一致性的前提下,最大化系统的吞吐量。
综上所述,B+树作为一种高效的数据结构,为数据库提供了强大的索引功能,极大地提高了数据检索的速度和效率,同时在大规模数据管理和并发控制方面也表现出色。
应用案例
B+树在数据库索引中的应用是最为典型的案例之一。让我们以一个具体的应用场景为例,假设我们有一个大型的在线零售数据库,其中包含数百万条客户订单记录。为了快速查询和管理这些数据,我们可以使用B+树作为索引。
场景描述
- 数据库表:
Orders - 主键:
OrderID(整数类型) - 其他字段:
CustomerID,ProductID,Quantity,OrderDate
索引创建
假设我们需要根据OrderID快速检索订单信息,我们可以创建一个基于OrderID的B+树索引。创建索引的过程涉及遍历所有订单记录,将OrderID作为键值,以及指向对应记录的指针作为值,构建一棵B+树。
查询操作
-
单一查询:如果我们需要查找特定
OrderID的订单信息,B+树可以迅速定位到正确的叶子节点,然后直接获取到该订单的所有详细信息,而无需全表扫描。 -
范围查询:假设我们需要找出所有在某个日期范围内的订单,我们可以利用B+树的叶子节点之间的链接特性,从起始日期对应的节点开始,沿着链表遍历到结束日期对应的节点,从而快速获取到所有符合条件的订单。
更新操作
当有新的订单产生时,即需要在B+树中插入新的键值对。B+树的设计确保了在插入新节点时,如果节点已满,则会进行分裂,生成一个新的节点,以保持树的平衡状态。同样,如果删除操作导致某个节点的键值对数量过少,B+树会进行合并操作,以避免树过于稀疏。
并发处理
在多用户同时进行查询和修改的情况下,数据库管理系统可以利用B+树的特性,对正在访问的节点进行锁定,防止其他事务修改这些数据,从而实现有效的并发控制,保证数据的一致性和完整性。
通过上述案例,我们可以看到B+树如何在实际的数据库应用中发挥重要作用,不仅显著提高了查询速度,而且支持高效的更新操作和并发处理,是数据库系统中不可或缺的核心技术之一。
Python代码示例
这里我将提供一个简单的Python代码示例,用于演示如何使用B树的基本操作,包括插入和搜索。请注意,由于B+树的复杂性,这里展示的是一个简化的B树(通常称为B-Tree),而不是完整的B+树实现,但原理相似,且可以帮助理解基本概念。
class BTreeNode:def __init__(self, leaf=False):self.keys = []self.children = []self.leaf = leafdef split_child(self, i, child):new_node = BTreeNode(leaf=child.leaf)self.children.insert(i + 1, new_node)self.keys.insert(i, child.keys.pop(len(child.keys) // 2))new_node.keys = child.keys[len(child.keys) // 2 + 1:]child.keys = child.keys[:len(child.keys) // 2]if not child.leaf:new_node.children = child.children[len(child.children) // 2 + 1:]child.children = child.children[:len(child.children) // 2 + 1]def insert_non_full(self, k):i = len(self.keys) - 1if self.leaf:self.keys.append(None)while i >= 0 and k < self.keys[i]:self.keys[i + 1] = self.keys[i]i -= 1self.keys[i + 1] = kelse:while i >= 0 and k < self.keys[i]:i -= 1i += 1if len(self.children[i].keys) == 2 * t - 1:self.split_child(i, self.children[i])if k > self.keys[i]:i += 1self.children[i].insert_non_full(k)def search(self, k):i = 0while i < len(self.keys) and k > self.keys[i]:i += 1if self.leaf:return i if i < len(self.keys) and self.keys[i] == k else Noneelse:return self.children[i].search(k)t = 3 # minimum degree of the tree
root = BTreeNode()
root.insert_non_full(10)
root.insert_non_full(20)
root.insert_non_full(5)
root.insert_non_full(6)
root.insert_non_full(12)
root.insert_non_full(30)
root.insert_non_full(7)
root.insert_non_full(17)print("Search for 20:", root.search(20)) # Should return the index where 20 is located
print("Search for 100:", root.search(100)) # Should return None as 100 is not in the tree
这段代码定义了一个B树节点类BTreeNode,实现了插入和搜索功能。注意,这里的B树的最小度数t被设置为3,这意味着每个非根节点至少有2个子节点(2 * t - 1是节点最多可以存储的键的数量)。这个简单的例子展示了如何在B树中插入元素,并搜索特定的键值。
请注意,这是一个高度简化的示例,不包括删除操作,也不包括所有错误检查和边界情况处理。在实际应用中,B树和B+树的实现会更加复杂和详尽。
在上一个代码示例中,我们介绍了B树的基本插入和搜索操作。然而,一个完整的B树或B+树实现还需要包括删除操作,以及更复杂的树调整策略,比如节点的合并等。下面,我会简单介绍如何在B树中实现删除操作,尽管不会给出完整代码,但会概述主要步骤。### 删除操作删除操作比插入和搜索要复杂得多,因为它可能导致树的不平衡。以下是删除操作的大致步骤:1. **查找要删除的键**:首先,使用搜索算法找到要删除的键所在的节点。2. **检查节点类型**:- 如果键位于叶节点,直接删除键。- 如果键位于非叶节点,需要找到后继或前驱键(通常是右子树中的最小键或左子树中的最大键),用它替换要删除的键,然后问题转化为删除叶节点中的键。3. **节点合并或再分配**:- 如果删除操作导致节点的键数量低于最小键数量(即节点不满),则需要从相邻兄弟节点中借键,或者与兄弟节点合并。- 如果与兄弟节点合并导致父节点不满,递归地向上合并,直到达到根节点或满足条件为止。### 示例代码框架下面是一个简化版的删除操作伪代码框架:```python
def delete(self, k):# Find the node containing the key knode, index = self._find_node(k)# If the key is found in a leaf node, simply remove itif node.leaf:node.keys.remove(k)# If the key is in an internal node, replace it with its successor or predecessorelse:# Find the successor/predecessorreplacement = self._find_replacement(node, index)# Replace the key with the successor/predecessornode.keys[index] = replacement# Now the problem becomes deleting the successor/predecessor from the leafself.delete(replacement)def _find_node(self, k):# Implement the search algorithm to find the node containing the key kpassdef _find_replacement(self, node, index):# Implement logic to find the successor or predecessorpassdef _borrow_or_merge(self, node):# Implement logic to borrow keys from siblings or merge nodespass
请注意,以上代码是高度抽象的,实际的实现将涉及到更详细的逻辑和边界情况处理,包括如何选择借键还是合并节点,以及如何递归地处理合并过程中可能产生的不平衡。
在处理删除操作时,确保树的平衡是至关重要的,因为不平衡可能导致查询性能下降。因此,一个健壮的B树或B+树实现需要仔细考虑所有可能的情况,并通过适当的调整策略来维护树的平衡。
————————————————
最后我们放松一下眼睛

相关文章:

B+树与索引解析
文章目录 B树与索引简介几个关键点应用案例场景描述索引创建查询操作更新操作并发处理 Python代码示例 B树与索引简介 B树是一种在计算机科学中广泛使用的自平衡的树数据结构,它能保持数据排序,并且搜索、插入和删除操作的时间复杂度都是O(log n)。B树被…...

华为认证hcna题库背诵技巧有哪些?hcna和hcia有什么区别?
大家都知道华为认证hcna是有题库供考生刷题备考的,但题库中海量的题目想要在短时间背诵下来可并不是一件容易的事情,这就需要我们掌握一定的技巧才行。华为认证hcna题库背诵技巧有哪些? hcna和hcna这二者又有什么区别呢?今天的文章将为大家进行详细解…...

【常用报文状态码】
常见的报文状态码如下 200 OK:客户端请求成功。 301 Moved Permanently:表示请求的资源已经被永久移动到了新的URL上; 302 Found:表示请求的资源已经被临时移动到了新的URL上; 304 Not Modified:表示客户…...
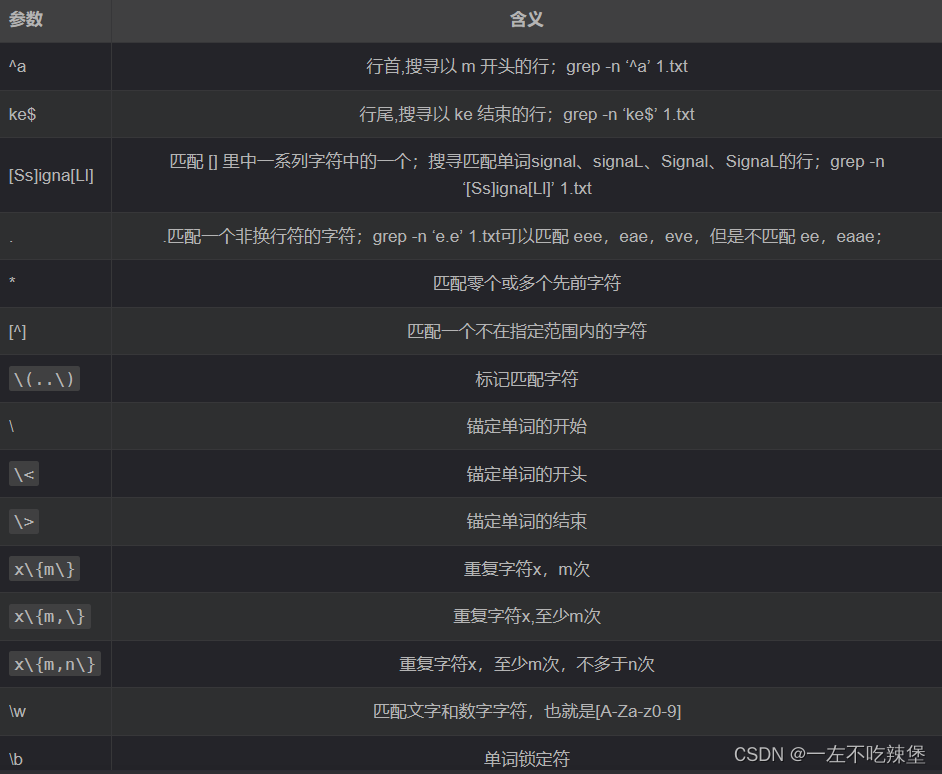
Linux命令详解
1.目录结构 2.history游览历史 3.命令行中的ctrl组合键 4.列出目录的内容 5.修改文件权限chmod 6.文件内容查看 文件管理 7.输出重定向:> 8.管道:| 9.清屏:clear 10.显示当前路径:pwd 11.创建目录:mkdir…...
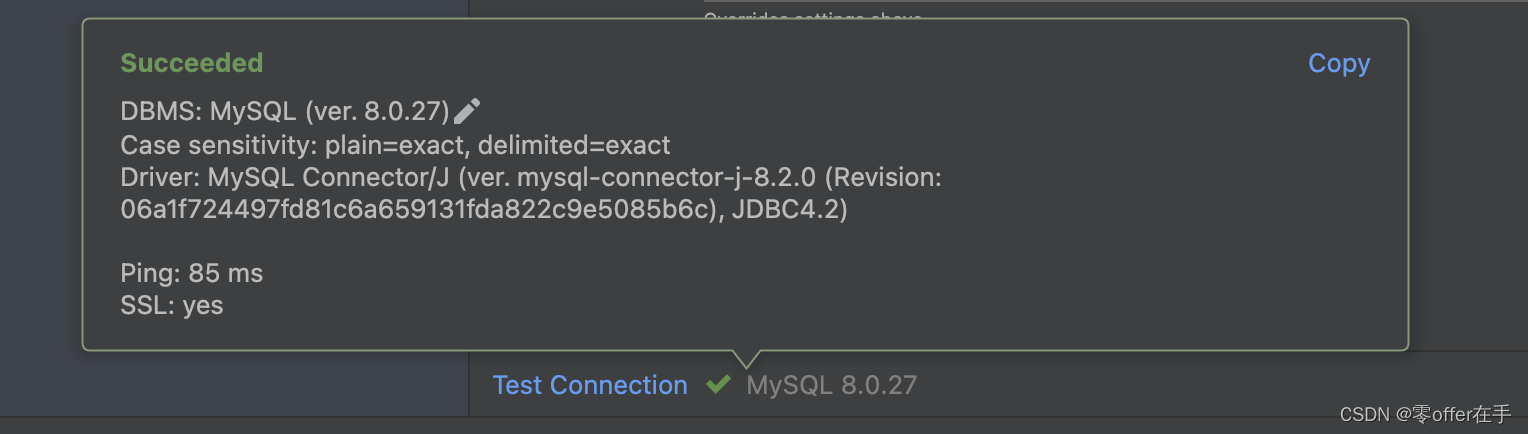
在阿里云使用Docker部署MySQL服务,并且通过IDEA进行连接
阿里云使用Docker部署MySQL服务,并且通过IDEA进行连接 这里演示如何使用阿里云来进行MySQL的部署,系统使用的是Linux系统 (Ubuntu)。 为什么使用Docker? 首先是因为它的可移植性可以在任何有Docker环境的系统上运行应用,避免了在不通操作系…...
实现技巧)
Spring Boot中的国际化(i18n)实现技巧
Spring Boot中的国际化(i18n)实现技巧 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!在开发多语言支持的应用程序时,国际化…...

vite-ts-cesium项目集成mars3d修改相关的包和配置参考
如果vite技术栈下使用原生cesium,请参考下面文件的包和配置修改,想用原生创建的viewer结合我们mars3d的功能的话。 1. package.json文件 "dependencies": {"cesium": "^1.103.0","mars3d": "^3.7.18&quo…...

「树莓派入门」树莓派基础04-VNC连接与配置静态IP
一、VNC连接配置 1. 启用VNC服务 在树莓派上,通过 raspi-config 工具启用VNC服务: sudo raspi-config在配置界面中选择 “Interfacing Options”,然后选择 “VNC” 并启用它。 2. 连接到VNC服务器 在电脑端安装VNC客户端,如V…...
JAVA编程题期末题库【中】
8.计算邮资 程序代码: public static void main(String[] args) {// 计算邮资//if多分支语句//创建对象java.util.Scanner inputnew java.util.Scanner(System.in); //提示输入用户,输入邮件的重量System.out.println("邮件的重量:");int wei…...

【十年JAVA搬砖路】——MYSQL备份使用mysqldump
使用mysqldump 备份 1.创建备份脚本 cat <<EOF > sqlback.sh source ~/.bashrc NLS_DATE_FORMAT"yyyy-mm-dd HH24:MI:SS"; export NLS_DATE_FORMAT NLS_LANGAMERICAN_AMERICA.ZHS16GBK;export NLS_LANGbackuptimedate %Y%m%d%H%M%S /usr/bin/mysqldump -u…...

MetaGPT全面安装与配置指南
文章目录 MetaGPT环境配置1.1 检查Python版本1.2 拉取MetaGPT仓库1.3 拉取源码本地安装1.4 MetaGPT安装成果全流程展示1.5 尝试简单使用 MetaGPT的API调用2.1 本地部署大模型尝试安装必要的依赖下载并配置大模型配置API服务 2.2 讯飞星火API调用获取API密钥安装讯飞星火SDK调用…...
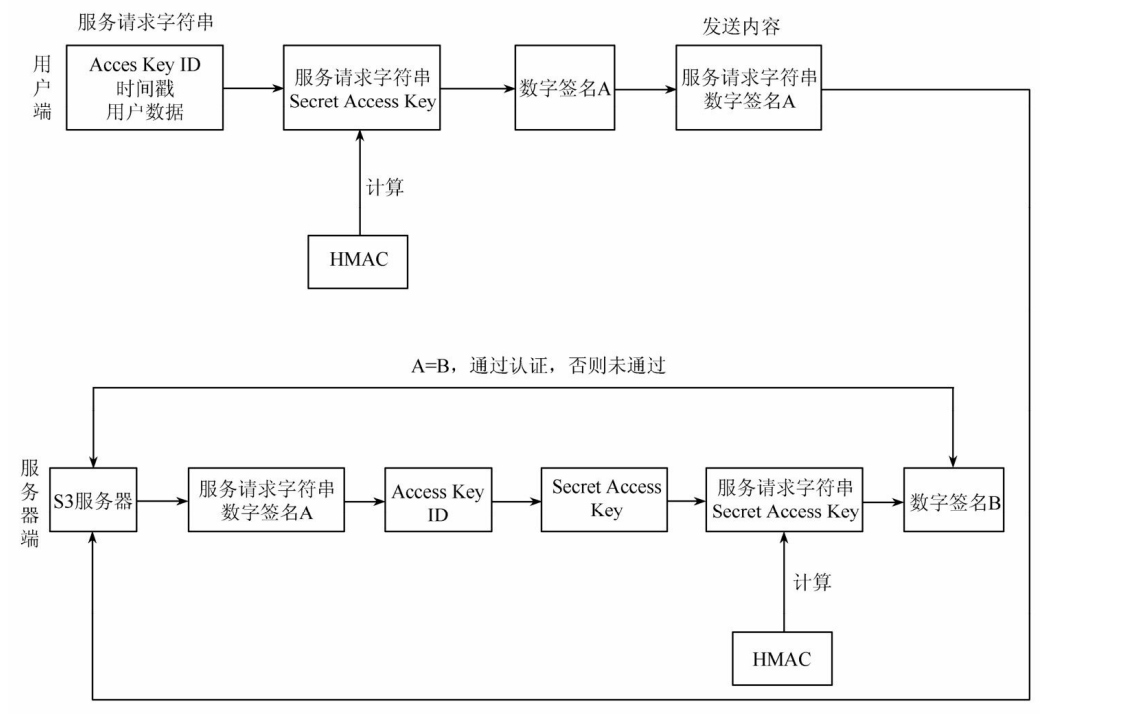
云计算期末综合测试题
云计算综合测试题 单选题填空题判断题简答题 单选题 这里选择题,直接以填空题展示,并给出解析 Bigtable是(Google)开发的分布式存储系统 解析:分布式结构化数据表Bigtable是Google基于GFS和Chubby开发的分布式存储系统…...
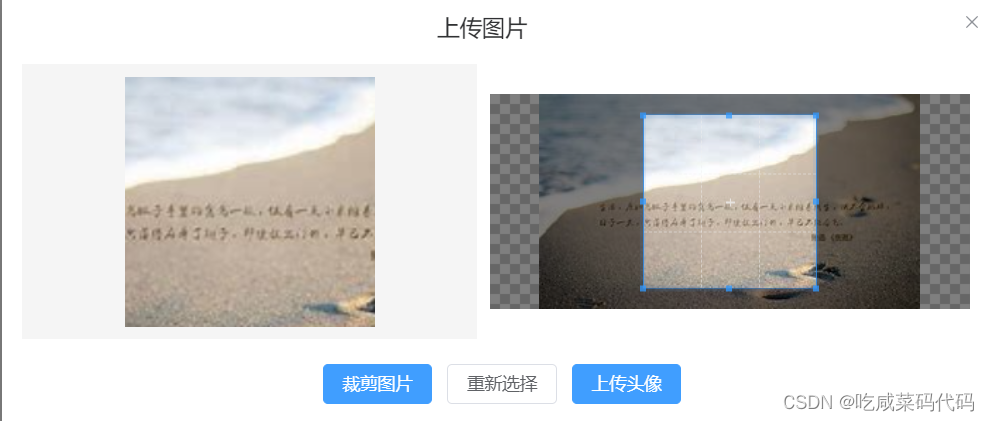
vue3-cropperjs图片裁剪工具-用户上传图片截取-(含预览视频)
效果图 上传图片弹窗预览 对于这个上传图片样式可以参考 官方原代码 官网传送入口 Upload 上传 | Element Plus (element-plus.org) <template><el-uploadclass"upload-demo"dragaction"https://run.mocky.io/v3/9d059bf9-4660-45f2-925d-ce80ad6…...
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第48课-可视化控制机器人
【WEB前端2024】3D智体编程:乔布斯3D纪念馆-第48课-可视化控制机器人 使用dtns.network德塔世界(开源的智体世界引擎),策划和设计《乔布斯超大型的开源3D纪念馆》的系列教程。dtns.network是一款主要由JavaScript编写的智体世界引…...

Java Stream API揭秘:掌握List流操作,打造高效数据处理流程
序言 Java Stream API是Java 8中引入的一个非常重要的功能组成部分,它提供了一种声明式的处理数据集合的方法。它主要特点是基于函数式编程的理念,允许我们以更加简洁、高效的方式进行集合的处理、转换和过滤。通过Stream API,我们可以灵活地…...
))
最新Java面试题及答案(Java基础、设计模式、Java虚拟机(jvm))
文章目录 前言一、Java基础题1.什么是Java?2.Jdk和Jre和JVM的区别?3.Java语言有哪些特点?4.Java有哪些数据类型?5.switch 是否能作用在 byte 上,是否能作用在 long 上,是否能作用在 String上?6.…...
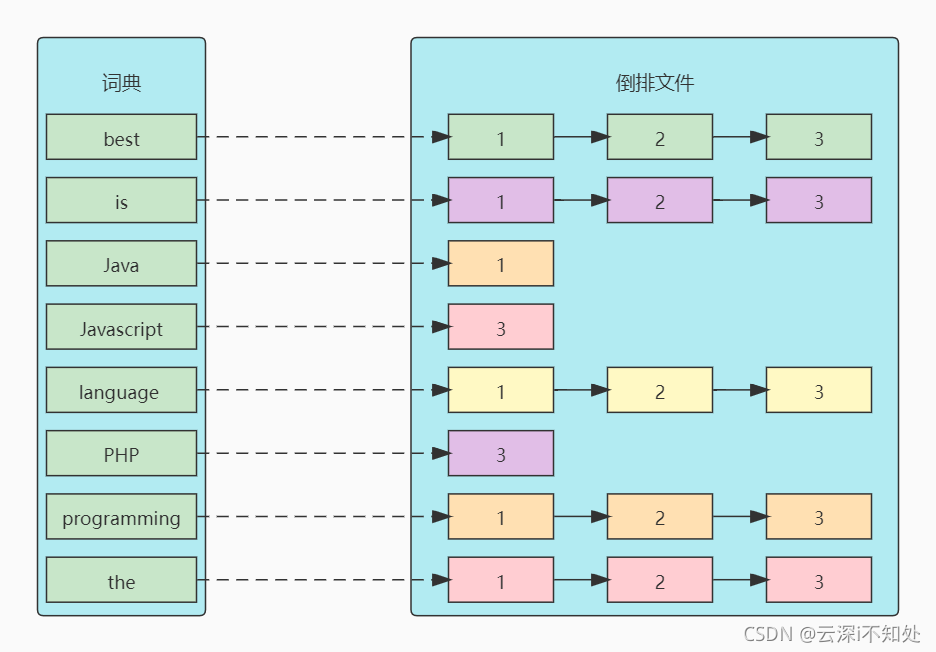
详解Elastic Search高速搜索背后的秘密:倒排索引
🎬 鸽芷咕:个人主页 🔥 个人专栏: 《C干货基地》《粉丝福利》 ⛺️生活的理想,就是为了理想的生活! 引入 全文搜索属于最常见的需求,开源的 Elasticsearch (以下简称 Elastic)是目前全文搜索引…...

数据库操控指南:玩转数据
对于表中数据的基本操作 数据的操作——DML语句(增删改)1.插入数据2.修改数据3.数据删除 数据的查询——DQL语句1.原理:2.查看表结构3.条件查询4.基础的SELECT语法 阅读指南: 本文章讲述了对于数据库中的数据的基本操作࿰…...

前端 CSS 经典:图层放大的 hover 效果
效果 思路 设置 3 层元素,最上层元素使用 clip-path 裁剪成圆,hover 改变圆大小,添加过渡效果。 实现代码 <!DOCTYPE html> <html lang"en"><head><meta charset"utf-8" /><meta http-eq…...

Flutter实现页面间传参
带参跳转 步骤 在router中配置这个路由需要携带的参数,这里的参数是 arguments,注意要用花括号包裹参数名称 在相应组件中实现带参构造函数 在state类中可以直接使用${widget.arguments}来访问到传递的参数 在其他页面中使用Navigator.pushNamed()带参跳转...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

Linux 中如何提取压缩文件 ?
Linux 是一种流行的开源操作系统,它提供了许多工具来管理、压缩和解压缩文件。压缩文件有助于节省存储空间,使数据传输更快。本指南将向您展示如何在 Linux 中提取不同类型的压缩文件。 1. Unpacking ZIP Files ZIP 文件是非常常见的,要在 …...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...
