洛谷U389682 最大公约数合并
这道题最后有一个性质没有想出来,感觉还是有一点遗憾。
性质一、贪心是不对的
8 11 11 16
虽然第一次选择8和16合并是最优的,但是如果合并两次的话8 11 11是最优的。
性质二 、有1的情况就是前k+1个,也就是说,很多情况下取前k+1都是最优的
性质三 如果某个数前面有它的因子,那么合并的时候可以不对 a 1 a_1 a1产生任何影响。同时,如果 b m o d a = 0 , b > a b \mod a=0,b>a bmoda=0,b>a那么 b b b一定比 a a a后合并,也就是说无影响合并只会发生在相同的数之间,因此我们把无影响的数提出来考虑,所以剩下的都是不同的。
性质四 如果所有的数都不同,那么全部都只会和 a 1 a_1 a1合并。在原来的数列中考虑合并形成的连通块。在连通块大小为2的情况时。设 a 1 < x < y a1<x<y a1<x<y,那么有 y − x > = g c d ( x , y ) y-x>=gcd(x,y) y−x>=gcd(x,y)所以, x + y − g c d ( x , y ) > = 2 x > a 1 + x x+y-gcd(x,y)>=2x>a_1+x x+y−gcd(x,y)>=2x>a1+x,不如直接合并 a 1 a_1 a1和 x x x。现在考虑连通块大小超过2的情况。假设某个连通块不包含 1 1 1,那么我们可以通过合并使得该联通块剩下两个数,其中有一个还没有与任何的数合并。Case 1: x < a 1 < y x<a_1<y x<a1<y,这时应该合并 x , a 1 x,a_1 x,a1最优,与原假设矛盾。Case 2: a 1 < = x < = y a_1<=x<=y a1<=x<=y,这时也是合并 a 1 , x a_1,x a1,x更优,所以假设错误。
所以,现在应该把前面有相同的和剩下的全部不同的数分成两个组,然后给这两组分配合并次数,难点就是要怎么求在给定的次数时全部不同组的选择方法,但是我没有坚定的往这个方面想。
性质五 假设给全部不同的数合并 k k k次,那么必然选择 1 , 2 , . . . , k − 1 1,2,...,k-1 1,2,...,k−1,只有第 k k k个是不确定的。考虑选择 a , b , c , d ( a < b < c < d ) a,b,c,d(a<b<c<d) a,b,c,d(a<b<c<d)的情况,那么合并如果是 a , c , d a,c,d a,c,d的话,那么 c o s t ( a , c , d ) − c o s t ( a , b , c ) = d − b + g c d ( a , c , d ) − g c d ( a , b , c ) > = g c d ( b , c ) + g c d ( c , d ) + g c d ( a , c , d ) − g c d ( a , b , c ) > 0 cost(a,c,d)-cost(a,b,c)=d-b+gcd(a,c,d)-gcd(a,b,c)>=gcd(b,c)+gcd(c,d)+gcd(a,c,d)-gcd(a,b,c)>0 cost(a,c,d)−cost(a,b,c)=d−b+gcd(a,c,d)−gcd(a,b,c)>=gcd(b,c)+gcd(c,d)+gcd(a,c,d)−gcd(a,b,c)>0,所以只用考虑第k个点怎么选,而且枚举范围有 a [ i ] − a [ k − 1 ] < g c d ( a 1 , a 2 , . . . , a k − 1 ) a[i]-a[k-1]<gcd(a_1,a_2,...,a_{k-1}) a[i]−a[k−1]<gcd(a1,a2,...,ak−1),这样显然是不超过 O ( n l o g n ) O(nlogn) O(nlogn)的。
相关文章:

洛谷U389682 最大公约数合并
这道题最后有一个性质没有想出来,感觉还是有一点遗憾。 性质一、贪心是不对的 8 11 11 16虽然第一次选择8和16合并是最优的,但是如果合并两次的话8 11 11是最优的。 性质二 、有1的情况就是前k1个,也就是说,很多情况下取前k1都…...

video_多个m3u文件合并成一个m3u文件
主要是用#EXT-X-DISCONTINUITY进行拼接,用简单的例子说明: 第一个文件: #EXTM3U #EXT-X-VERSION:3 #EXT-X-TARGETDURATION:69 #EXT-X-MEDIA-SEQUENCE:1001 #EXTINF:60.000000, xmt202406_11001.ts #EXTINF:60.000000, xmt202406_11002.ts #EXTINF:60.000000, xmt202406_11…...

x264 码率控制 MBtree 原理:i_propagate_cost计算过程
x264 码率控制 MBtree 原理 关于x264 码率控制中 MBtree 算法的原理具体可以参考:x264 码率控制MBtree原理。 i_propagate_cost介绍 该值在 frame.h 中 x264_frame_t结构体中声明。该值是一个 uint16_t型指针变量,在 MBtree 算法中用来存储每个宏块的传播代价。在*frame_ne…...
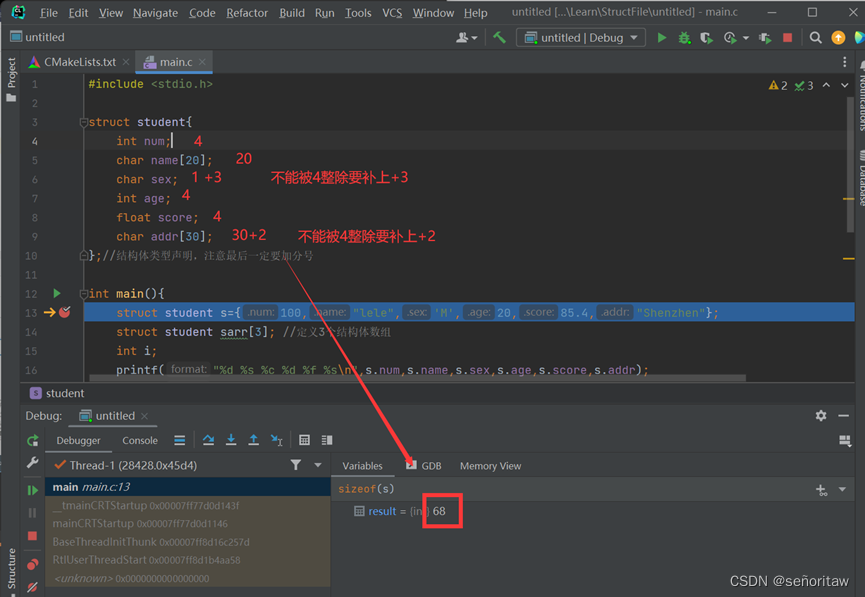
C语言基础笔记(全)
一、数据类型 数据的输入输出 1.数据类型 常量变量 1.1 数据类型 1.2 常量 程序运行中值不发生变化的量,常量又可分为整型、实型(也称浮点型)、字符型和字符串型 1.3 变量 变量代表内存中具有特定属性的存储单元,用来存放数据,即变量的值&a…...
)
通过注释语句,简化实体类的定义(省略get/set/toString的方法)
引用Java的lombok库,减少模板代码,如getters、setters、构造函数、toString、equals和hashCode方法等 import lombok.AllArgsConstructor; import lombok.Data; import lombok.NoArgsConstructor;Data NoArgsConstructor AllArgsConstructorData…...
springboot框架使用Netty依赖中解码器的作用及实现详解
在项目开发 有需求 需要跟硬件通信 也没有mqtt 作为桥接 也不能http 请求 api 所以也不能 json字符串这么爽传输 所以要用tcp 请求 进行数据交互 数据还是16进制的 写法 有帧头 什么的 对于这种物联网的这种对接 我的理解就是 我们做的工作就像翻译 把这些看不懂的 字节流 变成…...

Python爬虫实战之爬取京东商品数据
在数字化时代,数据如同黄金般珍贵,而电商数据,尤其是像京东这样的大型电商平台上的信息,更是商家、市场分析师和数据科学家眼中的瑰宝。本文将带您走进Python爬虫的世界,探索如何高效、合法地采集京东商品数据…...

浅析Resource Quota中limits计算机制
前言 在生产环境中,通常需要通过配置资源配额(Resource Quota)来限制一个命名空间(namespace)能使用的资源量。在资源紧张的情况下,常常需要调整工作负载(workload)的请求值…...
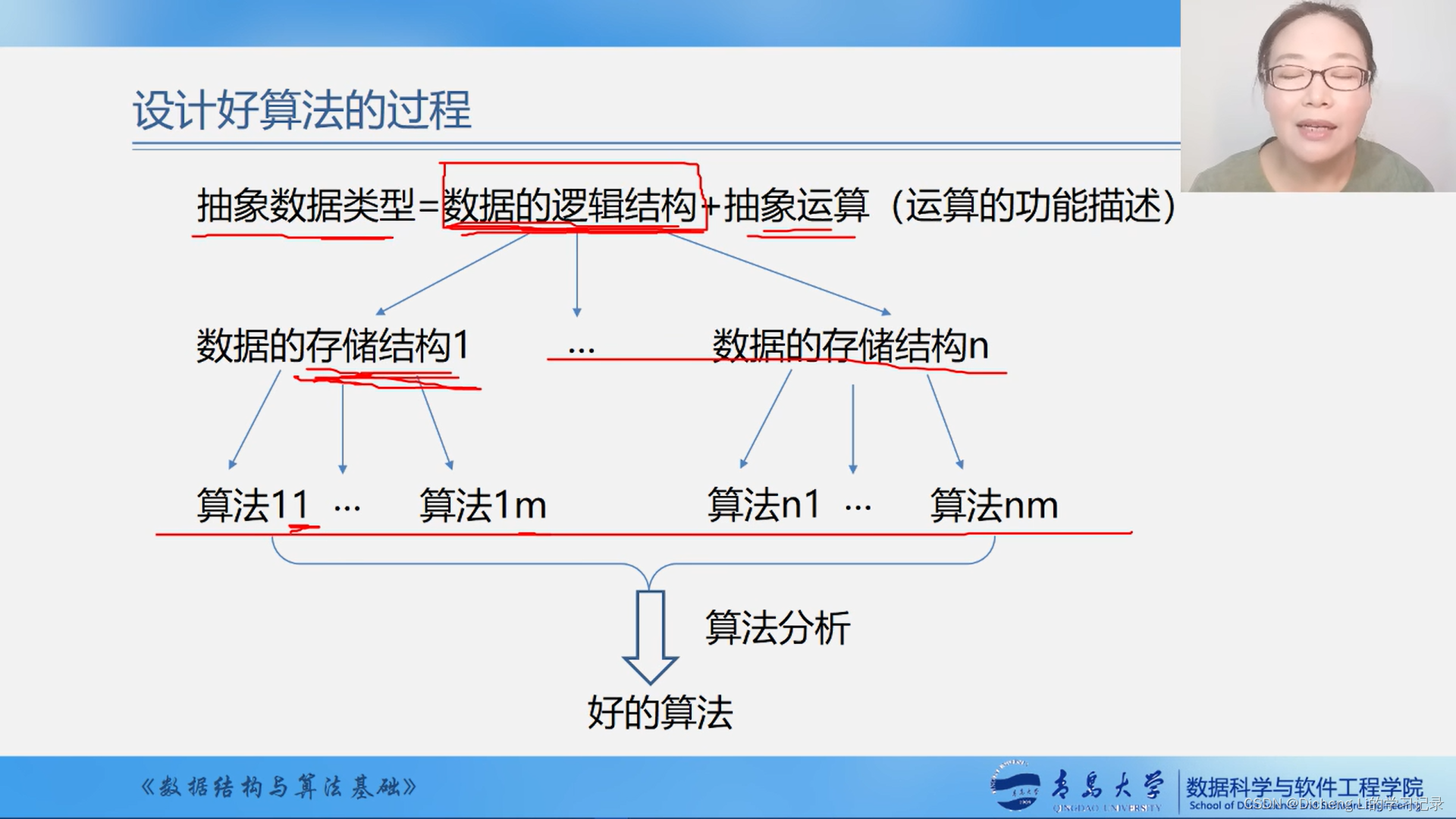
《数据结构与算法基础 by王卓老师》学习笔记——1.4算法与算法分析
一、算法 1.1算法的研究内容 1.2算法的定义 1.3算法的描述 以下是算法的自然语言描述 以下是算法的传统流程图表示 以下是NS流程图表示 1.4算法和程序的区别与联系 1.5算法的五个特性 1.6算法设计的要求 Robustness也称为鲁棒性 二、算法分析 2.1算法时间效率的度量 2.1.1事…...

运维团队如何加强安全设备监控与日志管理
随着信息技术的飞速发展,网络安全问题日益凸显,安全设备的监控和日志管理成为了运维团队不可或缺的工作内容。本文将结合运维行业的实际需求,探讨如何加强安全设备监控与日志管理,以提升系统的安全性和稳定性。 一、安全设备监控…...

仓库管理系统13--物资设置
1、添加窗体 2、设计UI界面 注意这个下拉框的绑定,你看到的选项是由displaymember决定,当你选择了哪个选项时,后台绑定这个选项的ID <UserControl x:Class"West.StoreMgr.View.GoodsView"xmlns"http://schemas.microsoft…...
机器人控制系列教程之URDF文件语法介绍
前两期推文:机器人控制系列教程之动力学建模(1)、机器人控制系列教程之动力学建模(2),我们主要从数学的角度介绍了机器人的动力学建模的方式,随着机器人技术的不断发展,机器人建模成为了机器人系统设计中的一项关键任务。URDF&…...

Arathi Basin (AB) PVP15
Arathi Basin (AB) PVP15 阿拉希盆地,PVP,15人战场...

Ubuntu/Linux SSH 端口转发
文章目录 Ubuntu/Linux SSH 端口转发概述本地端口转发场景一场景二 参考资料 Ubuntu/Linux SSH 端口转发 概述 SSH, Secure Shell 是一种在网络上用于安全远程登录到另一台机器的工具。除了远程登录以外,ssh 的端口转发是它的另一项强大功能。通过 ssh 端口转发功…...

flask的locked_cached_property
下面是一个关于 locked_cached_property 装饰器的详细教程。这个装饰器将一个方法转换为一个惰性属性,在第一次访问时计算其值,并在随后的访问中缓存该值。同时,它在多线程环境中是线程安全的。 教程:理解和使用 locked_cached_p…...
OSI七层模型TCP/IP四层面试高频考点
OSI七层模型&TCP/IP四层&面试高频考点 1 OSI七层模型 1. 物理层:透明地传输比特流 在物理媒介上传输原始比特流,定义了连接主机的硬件设备和传输媒介的规范。它确保比特流能够在网络中准确地传输,例如通过以太网、光纤和无线电波等媒…...

Swagger2及常用校验注释说明
Api(value "后台用户管理") RestController RequestMapping("bossuser") public class BossUserController {ApiOperation(value "测试接口")PostMapping("test")public String testUser(Valid RequestBody TestUser user) {LOG.inf…...
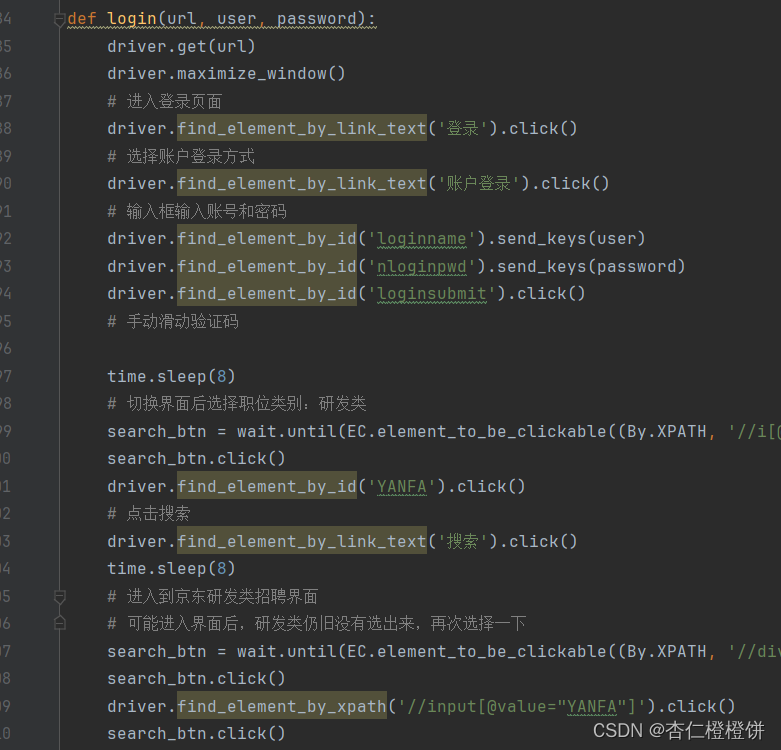
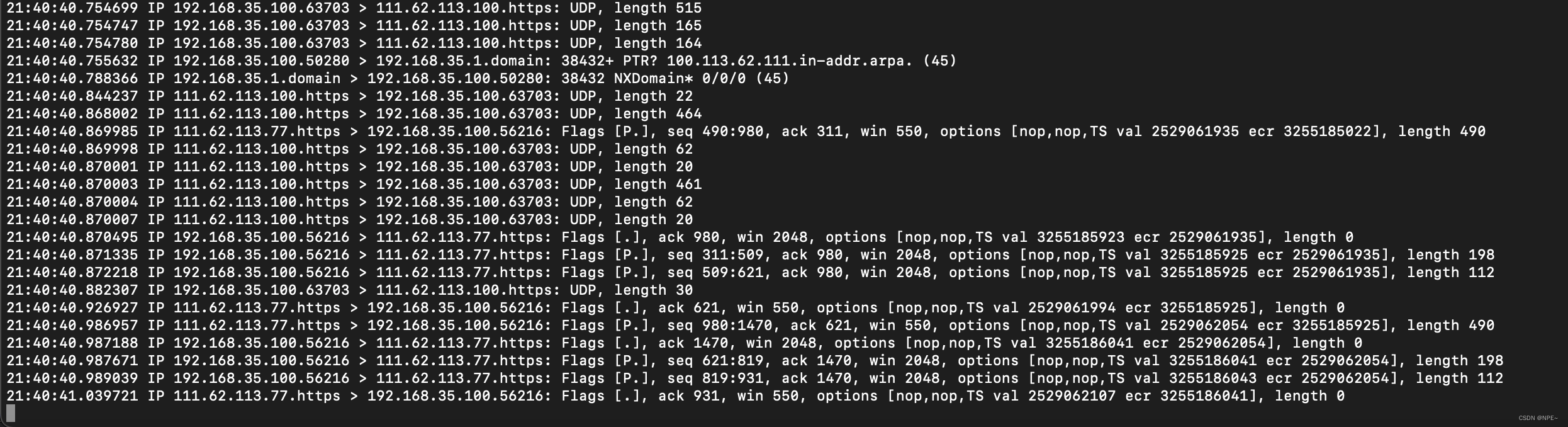
【项目实训】各种反爬策略及爬虫困难点总结
在这里,我总结了本次项目的数据收集过程中遇到的反爬虫策略以及一些爬虫过程中容易出现问题的地方。 user-agent 简单的设置user-agent头部为浏览器即可: 爬取标签中带href属性的网页 对于显示岗位列表的页面,通常检查其源代码就会发现&…...

能量智慧流转:全面升级储能电站的智能网关解决方案
监控系统是电化学储能电站的关键组成部分,储能电站也需要相应的监控系统,通过监控系统对储能设备的状态进行监测,实时感知储能设备的健康状态,控制储能设备的充放电功率和时机等, 一个好的监控系统可以实现储能电站安全…...
【金融研究】6月,对冲基金狂卖美国科技股 短期乐观,长期悲观?“油价最大空头”花旗:明年跌到60
科技股新高的背后,是对冲基金与散户投资者的分歧,对冲基金正在向散户投资者出售创纪录数量的科技/半导体/美股“七姐妹”股票。 对冲基金狂卖美国科技股 在五大明星科技股(苹果、亚马逊、微软、英伟达、谷歌)轮番创下历史新高的…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

R 语言科研绘图第 55 期 --- 网络图-聚类
在发表科研论文的过程中,科研绘图是必不可少的,一张好看的图形会是文章很大的加分项。 为了便于使用,本系列文章介绍的所有绘图都已收录到了 sciRplot 项目中,获取方式: R 语言科研绘图模板 --- sciRplothttps://mp.…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...
