概率论与数理统计期末复习
概率论常考知识点汇总







总括
1. 基础概率论
- 概率定义:理解概率是事件发生的可能性度量,范围从0(不可能)到1(必然发生)。
- 概率公理:掌握概率的三大公理,即非负性、规范性和可加性。
- 条件概率:P(A|B)表示在事件B已发生的条件下,事件A发生的概率。
- 贝叶斯定理:用于计算在已知某些证据或数据的条件下,某个假设为真的概率。
- 独立事件与相关事件:理解独立事件的概率乘法规则及相关事件的处理方法。
2. 随机变量及其分布
- 离散随机变量:了解伯努利分布、二项分布、泊松分布等,以及它们的应用场景。
- 连续随机变量:熟悉均匀分布、正态分布(高斯分布)、指数分布等,掌握其概率密度函数(PDF)和累积分布函数(CDF)。
- 联合分布与边缘分布:理解多维随机变量的联合分布,及其边缘分布的计算方法。
- 条件分布与协方差:学习如何基于给定条件下一个随机变量的分布,以及随机变量间的相互依赖关系。
3. 数理统计基础
- 点估计:了解均值、中位数、众数作为参数的估计方法,以及最大似然估计和最小二乘法。
- 区间估计:掌握置信区间的概念,理解如何构建参数的置信区间,特别是正态分布情况下的Z检验和t检验。
- 假设检验:熟悉原假设与备择假设,掌握单样本和双样本检验,包括显著性水平、p值的理解与应用。
- 方差分析(ANOVA):理解方差分析的基本原理,用于比较两个以上样本均值是否存在显著差异。
4. 高级主题(根据兴趣选择)
- 贝叶斯统计:深入理解贝叶斯分析,包括先验概率、后验概率和贝叶斯推断。
- 大数定律与中心极限定理:掌握这两个定理对于统计推断的重要意义。
- 非参数统计:了解当数据不符合正态分布或其他特定分布时,使用如卡方检验、秩和检验等非参数方法。
- 时间序列分析:研究随时间变化的数据序列,涉及自回归模型(AR)、移动平均模型(MA)及它们的组合ARIMA等。
基本概率公式
在概率论中,事件之间的关系及其运算主要涉及交集、并集、补事件以及条件概率,这些是理解和计算复合事件概率的基础。下面详细解释这些概念:
1. 交集 (Intersection)
- 定义:如果A和B是两个事件,那么A∩B表示事件A和事件B同时发生的事件。即A和B的交集包含了所有既属于A又属于B的样本点。
- 概率运算:事件A和B同时发生的概率,记作P(A∩B),等于各自发生的概率的乘积,仅当A和B是独立事件时,即P(A∩B) = P(A) * P(B)。若A和B不独立,则需要根据具体情况计算。
2. 并集 (Union)
-
定义:事件A和B的并集,记作A∪B,包含所有至少属于A或B(或两者都属于)的样本点。
-
概率运算
:事件A或B至少有一个发生的概率,记作P(A∪B),可以通过以下公式计算:
𝑃(𝐴∪𝐵)=𝑃(𝐴)+𝑃(𝐵)−𝑃(𝐴∩𝐵)P(A∪B)=P(A)+P(B)−P(A∩B)
这里减去P(A∩B)是为了避免A和B共同部分被重复计算。
3. 补事件 (Complement)
- 定义:对于任意事件A,它的补事件记作A’或𝐴ˉAˉ,表示A不发生的事件。
- 概率运算:一个事件与其补事件的概率之和等于1,即P(A’) = 1 - P(A)。补事件的概念简化了某些问题的处理,特别是在计算“至少”或“至多”这类问题时。
4. 条件概率 (Conditional Probability)
-
定义:在事件B已经发生的条件下,事件A发生的概率,记作P(A|B)。
-
计算公式
:
𝑃(𝐴∣𝐵)=𝑃(𝐴∩𝐵)𝑃(𝐵)P(A∣B)=P(B)P(A∩B)
只有当P(B) > 0时,上述公式才有意义。
5. 乘法法则 (Multiplication Rule)
-
用于计算两个事件同时发生的概率,特别地,它也关联条件概率和无条件概率的关系:
𝑃(𝐴∩𝐵)=𝑃(𝐴)⋅𝑃(𝐵∣𝐴)=𝑃(𝐵)⋅𝑃(𝐴∣𝐵)P(A∩B)=P(A)⋅P(B∣A)=P(B)⋅P(A∣B)
这表明可以从不同的角度理解两个事件同时发生的概率
随机变量
随机变量
定义:随机变量是将随机试验的结果与实数建立对应关系的函数。它可以分为两种类型:
- 离散随机变量:取值为有限个或可数无限个确定值的随机变量,如抛掷一枚骰子得到的点数。
- 连续随机变量:取值可以在某个区间内取任何值(理论上无限多)的随机变量,如测量一个人的身高。
分布函数
定义:随机变量 𝑋X 的分布函数(Cumulative Distribution Function, CDF),记作 𝐹(𝑥)F(x),定义为随机变量 𝑋X 取值小于或等于 𝑥x 的概率。形式上,对于任意实数 𝑥x,有:
𝐹(𝑥)=𝑃(𝑋≤𝑥)F(x)=P(X≤x)
性质:
- 单调性:分布函数 𝐹(𝑥)F(x) 是单调不减的,即如果 𝑥1<𝑥2x1<x2,则 𝐹(𝑥1)≤𝐹(𝑥2)F(x1)≤F(x2)。
- 右连续性:𝐹(𝑥)F(x) 在每一个点 𝑥x 处都是右连续的,意味着 𝐹(𝑥)F(x) 在 𝑥x 的右侧极限存在,并等于 𝐹(𝑥)F(x) 在 𝑥x 处的值。
- 边界条件:分布函数在 −∞−∞ 处为 0,在 +∞+∞ 处为 1,即 𝐹(−∞)=0F(−∞)=0,𝐹(+∞)=1F(+∞)=1。
- 概率计算:对于任意两个实数 𝑎a 和 𝑏b,若 𝑎<𝑏a<b,则随机变量 𝑋X 落在区间 (𝑎,𝑏](a,b] 内的概率为 𝑃(𝑎<𝑋≤𝑏)=𝐹(𝑏)−𝐹(𝑎)P(a<X≤b)=F(b)−F(a)。
分布函数的分类
- 离散随机变量的分布函数:通常是阶梯函数,每一步的跳跃高度代表相应值的概率质量。
- 连续随机变量的分布函数:对于连续型随机变量,分布函数是连续的,而概率密度函数 𝑓(𝑥)f(x) 与分布函数的关系为 𝐹′(𝑥)=𝑓(𝑥)F′(x)=f(x) 在 𝑓(𝑥)f(x) 连续的地方成立,即分布函数的导数(在定义的地方)给出了概率密度。
离散型概率以及分布
离散型概率分布描述的是离散随机变量取不同值的概率。离散随机变量只能取有限个或可数无限个值,每个值都有一个明确的概率与之对应。下面是几个典型的离散型概率分布及其特征:
1. 伯努利分布 (Bernoulli Distribution)
- 定义:伯努利试验是指只有两种可能结果的试验,通常称为“成功”和“失败”,且每次试验这两种结果的概率保持不变。设成功的概率为 𝑝p,失败的概率为 1−𝑝1−p,则一个伯努利随机变量 𝑋X 取值为1(成功)的概率为 𝑝p,取值为0(失败)的概率为 1−𝑝1−p。
- 概率质量函数 (PMF):𝑃(𝑋=𝑘)=𝑝𝑘(1−𝑝)1−𝑘P(X=k)=pk(1−p)1−k,其中 𝑘=0,1k=0,1。
2. 二项分布 (Binomial Distribution)
- 定义:在一系列独立的伯努利试验中,成功次数的分布称为二项分布。如果进行了 𝑛n 次独立的伯努利试验,每次试验成功的概率为 𝑝p,则在这些试验中恰好成功 𝑘k 次的概率服从二项分布。
- PMF:𝑃(𝑋=𝑘)=(𝑛𝑘)𝑝𝑘(1−𝑝)𝑛−𝑘P(X=k)=(kn)pk(1−p)n−k,其中 (𝑛𝑘)(kn) 是组合数,表示从 𝑛n 个不同元素中取出 𝑘k 个元素的组合方式数量。
3. 泊松分布 (Poisson Distribution)
- 定义:泊松分布常用来描述在一定时间或空间区域内,稀有事件发生次数的概率分布。如果平均每单位时间(或空间)内事件发生的次数为 𝜆λ,则在任意时间(或空间)区间内事件发生 𝑘k 次的概率遵循泊松分布。
- PMF:𝑃(𝑋=𝑘)=𝜆𝑘𝑒−𝜆𝑘!P(X=k)=k!λke−λ,其中 𝜆λ 是平均事件数,𝑒e 是自然对数的底。
4. 几何分布 (Geometric Distribution)
- 定义:几何分布描述的是首次成功前进行试验的次数。在一个伯努利试验序列中,直到首次成功所需试验的次数 𝑋X 服从几何分布,每次试验成功的概率为 𝑝p。
- PMF:𝑃(𝑋=𝑘)=(1−𝑝)𝑘−1𝑝P(X=k)=(1−p)k−1p,𝑘=1,2,3,…k=1,2,3,…。
5. 负二项分布 (Negative Binomial Distribution)
- 定义:负二项分布描述的是在第 𝑟r 次成功之前已经发生了 𝑘k 次失败的概率分布。它扩展了几何分布,考虑了达到固定成功次数前的失败次数。
- PMF:𝑃(𝑋=𝑘)=(𝑘+𝑟−1𝑘)𝑝𝑟(1−𝑝)𝑘P(X=k)=(kk+r−1)pr(1−p)k,其中 𝑟r 是预先设定的成功次数。
组合公式
组合公式是用来计算从n个不同元素中不重复地选择r个元素的方法数,记作 𝐶(𝑛,𝑟)C(n,r) 或者 “𝑛n 选 𝑟r”,也称为二项式系数。公式如下:
𝐶(𝑛,𝑟)=𝑛!𝑟!(𝑛−𝑟)!C(n,r)=r!(n−r)!n!
其中,
- 𝑛!n! 表示n的阶乘,即 𝑛×(𝑛−1)×(𝑛−2)×⋯×1n×(n−1)×(n−2)×⋯×1,
- 𝑟!r! 是r的阶乘,
- 𝑛−𝑟n−r 代表剩余未被选择的元素数量,
- "!"符号表示阶乘运算。
当 𝑛<𝑟n<r 时,𝐶(𝑛,𝑟)C(n,r) 定义为0,因为无法从较少的元素中选择更多的元素。
这个公式在概率论、统计学、组合数学以及日常生活中解决排列组合问题时非常有用。
连续型随机变量
连续性随机变量是概率论中的一种重要概念,它用来描述那些可能取值无法逐一列举,而是在某个区间内可以取任意实数值的随机变量。与离散型随机变量不同,连续型随机变量在数轴上的取值是连续的,其概率分布需要用概率密度函数(probability density function, PDF)来描述,而不是概率质量函数。以下是连续性随机变量的详细解析:

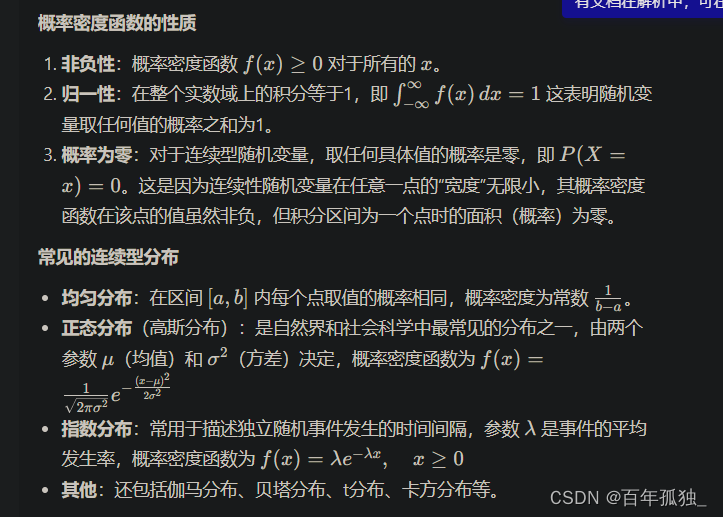
常见的连续型随机变量的及其分布

离散型随机变量函数的分布
离散型随机变量函数的分布是指如果有一个离散型随机变量 𝑋X,其概率质量函数(probability mass function, PMF)为 𝑃(𝑋=𝑥𝑖)=𝑝𝑖P(X=xi)=pi,对于 𝑋X 的某个函数 𝑌=𝑔(𝑋)Y=g(X),我们想要找到 𝑌Y 的分布,即求解 𝑌Y 的概率质量函数 𝑃(𝑌=𝑦𝑗)P(Y=yj)。
处理离散型随机变量函数分布的一般步骤如下:
- 确定 𝑌Y 的可能值:首先需要明确通过函数 𝑔g 转换后,𝑌Y 可能取到的所有值。这通常需要考虑 𝑋X 的所有可能取值,并应用 𝑔g 函数。
- 计算每个 𝑦𝑗yj 的概率:对于 𝑌Y 的每一个可能值 𝑦𝑗yj,需要找出所有能使 𝑔(𝑋)=𝑦𝑗g(X)=yj 的 𝑋X 的值集合 𝑆𝑗Sj,然后将这些 𝑋X 值对应的概率相加来得到 𝑃(𝑌=𝑦𝑗)P(Y=yj)。
𝑃(𝑌=𝑦𝑗)=∑𝑥𝑖∈𝑆𝑗𝑃(𝑋=𝑥𝑖)P(Y=yj)=∑xi∈SjP(X=xi)
这里,𝑆𝑗Sj 是使得 𝑔(𝑥𝑖)=𝑦𝑗g(xi)=yj 成立的所有 𝑥𝑖xi 的集合。
- 特殊情况处理:如果函数 𝑔g 导致某些 𝑌Y 的值没有对应的 𝑋X 值(即 𝑔g 不是满射),则那些 𝑌Y 的值的概率为0。反之,如果 𝑔g 将多个 𝑋X 映射到同一个 𝑌Y 值,则需要累加这些 𝑋X 值的概率。
举例说明:
假设 𝑋X 是一个离散型随机变量,取值为 {1, 2, 3},相应的概率分别为 1331。考虑函数 𝑌=𝑔(𝑋)=𝑋2Y=g(X)=X2。
- 确定 𝑌Y 的可能值:应用 𝑔g 后,𝑌Y 的可能值为 {1, 4, 9}。
- 计算每个 𝑦𝑗yj 的概率:
- 对于 𝑌=1Y=1,只有当 𝑋=1X=1 时成立,因此 𝑃(𝑌=1)=𝑃(𝑋=1)=13P(Y=1)=P(X=1)=31。
- 对于 𝑌=4Y=4,只有当 𝑋=2X=2 时成立,所以 𝑃(𝑌=4)=𝑃(𝑋=2)=13P(Y=4)=P(X=2)=31。
- 对于 𝑌=9Y=9,只有当 𝑋=3X=3 时成立,故 𝑃(𝑌=9)=𝑃(𝑋=3)=13P(Y=9)=P(X=3)=31。
最终,我们得到了 𝑌Y 的概率质量函数 𝑃(𝑌=1)=13P(Y=1)=31, 𝑃(𝑌=4)=13P(Y=4)=31, 𝑃(𝑌=9)=13P(Y=9)=31,这表明 𝑌Y 也是一个均匀分布的离散型随机变量。
二维连续型随机变量及其分布
二维连续性随机变量指的是由两个连续随机变量构成的随机向量,它们可以同时描述两个相互关联的连续随机现象。二维连续性随机变量的联合分布由联合概率密度函数(Joint Probability Density Function, JPDF)来描述,而边缘分布则描述了每个变量单独的分布情况。以下是二维连续性随机变量及其分布的详细说明:


协方差

计算协方差
计算协方差的具体步骤可以通过一个简单的例子来说明。假设我们有一组关于两个变量 𝑋X 和 𝑌Y 的数据对,分别是:
| 𝑋X | 𝑌Y |
|---|---|
| 2 | 4 |
| 4 | 6 |
| 6 | 8 |
| 8 | 10 |
首先,我们计算每个变量的平均值(均值):
𝐸[𝑋]=2+4+6+84=204=5E[X]=42+4+6+8=420=5𝐸[𝑌]=4+6+8+104=284=7E[Y]=44+6+8+10=428=7
接下来,我们使用样本协方差的公式来计算协方差:
𝐶𝑜𝑣^(𝑋,𝑌)=1𝑛−1∑𝑖=1𝑛(𝑥𝑖−𝑥‾)(𝑦𝑖−𝑦‾)Cov(X,Y)=n−11∑i=1n(xi−x)(yi−y)
其中 𝑛=4n=4 是样本量,𝑥‾=5x=5 是 𝑋X 的均值,𝑦‾=7y=7 是 𝑌Y 的均值。现在,我们计算每一项并求和:
- 对于第一对数据(2, 4):(2−5)(4−7)=(−3)(−3)=9(2−5)(4−7)=(−3)(−3)=9
- 对于第二对数据(4, 6):(4−5)(6−7)=(−1)(−1)=1(4−5)(6−7)=(−1)(−1)=1
- 对于第三对数据(6, 8):(6−5)(8−7)=(1)(1)=1(6−5)(8−7)=(1)(1)=1
- 对于第四对数据(8, 10):(8−5)(10−7)=(3)(3)=9(8−5)(10−7)=(3)(3)=9
现在,将这些乘积相加并应用公式:
𝐶𝑜𝑣^(𝑋,𝑌)=14−1×(9+1+1+9)=13×20=203Cov(X,Y)=4−11×(9+1+1+9)=31×20=320
因此,变量 𝑋X 和 𝑌Y 之间的样本协方差大约为 6.676.67。这个正值表明 𝑋X 和 𝑌Y 之间存在正相关关系,即随着 𝑋X 的增加,𝑌Y 也倾向于增加。

相关文章:

概率论与数理统计期末复习
概率论常考知识点汇总 总括 1. 基础概率论 概率定义:理解概率是事件发生的可能性度量,范围从0(不可能)到1(必然发生)。概率公理:掌握概率的三大公理,即非负性、规范性和可加性。条…...
python 识别图片点击,设置坐标,离设置坐标越近的优先识别点击
import pyautogui import cv2 import numpy as np import mathdef find_and_click(template_path, target_x, target_y, match_threshold0.8):"""在屏幕上查找目标图片并点击。Args:template_path: 目标图片的路径。target_x: 预设的坐标 x 轴值。target_y: 预设…...

【实战教程】如何使用JMeter来轻松测试WebSocket接口?
1、websocket接口原理 打开网页:从http协议,升级到websocket协议,请求建立websocket连接服务器返回建立成功成功客户端向服务端发送匹配请求服务端选择一个客服上线服务器返回客服id客户端向服务器发送消息服务器推送消息给指定的客服服务器…...

【linux】详解——库
目录 概述 库 库函数 静态库 动态库 制作动静态库 使用动静态库 如何让系统默认找到第三方库 lib和lib64的区别 /和/usr/和/usr/local下lib和lib64的区别 环境变量 配置相关文件 个人主页:东洛的克莱斯韦克-CSDN博客 简介:C站最萌博主 相关…...

RuntimeError: “exp_vml_cpu“ not implemented for ‘Half‘
遇到 "exp_vml_cpu" not implemented for Half 这个运行时错误,意味着你尝试在一个操作中使用了半精度(Half 或 float16)数据类型,但是该操作在当前环境下并没有针对半精度数据类型的实现。 半精度(float16&…...

JVM之双亲委派机制
1.双亲委派机制 在Java中,类加载器具有层次结构。每个Java实现的类加载器中保存了一个成员变量叫“父”类加载器(parent),可以理解为上级,并不是继承关系。应用程序类加载器的parent父加载器是扩展类加载器࿰…...

Gemalto SafeNet Luna HSM服务器硬件监控指标解读
在现代化的信息安全体系中,硬件安全模块(HSM)扮演着至关重要的角色,它负责保护和管理敏感的数据和密钥。Gemalto SafeNet Luna HSM作为一款高性能的硬件安全模块,广泛应用于金融、政府和企业等领域。为了确保Luna HSM的…...

计算机视觉与人工智能领域常用期刊和会议缩写
在撰写论文时有时候会面临超篇幅的情况,这时候一个常用的操作便是使用期刊(会议)的缩写或者半缩写来替换期刊(会议)全称 为了方便自己后续使用相关的缩写 特此整理 如有不当之处 欢迎大家指正~~ 计算机视觉与人工智能…...
ONLYOFFICE桌面编辑器8.1版:个性化编辑和功能强化的全面升级
ONLYOFFICE是一款全面的办公套件,由Ascensio System SIA开发。该软件提供了一系列与微软Office系列产品相似的办公工具,包括处理文档(ONLYOFFICE Document Editor)、电子表格(ONLYOFFICE Spreadsheet Editor࿰…...
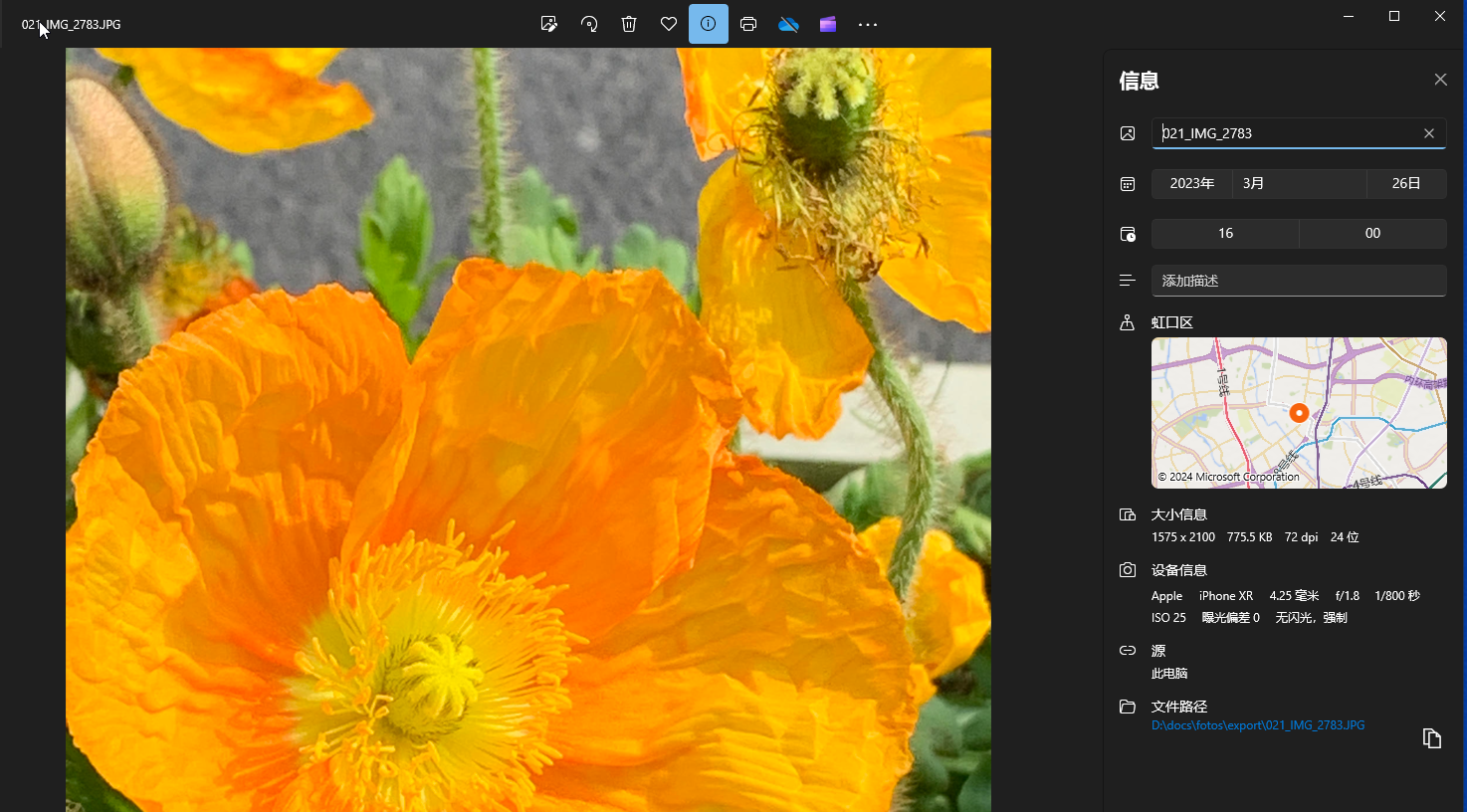
用一个实例看如何分享大量照片 续篇二,关于Exif (Exchangeable Image File) - 可交换图像文件
续篇二:说说关于照片隐含的 Exif (Exchangeable Image File) 可交换图像文件 数码照片的Exif 参数有很多,重要的Exif信息:拍摄日期、时间、拍摄器材、GPS信息。 当然这主要对自己的档案有意义,如果放到网上还是建议抹去这些信息。…...

使用Python自动化收集和处理视频资源的教程
在这篇教程中,我们将介绍如何利用Python脚本自动化收集和处理视频资源。这篇文章将帮助您掌握基本的网络自动化技术,并使用相关库进行视频资源的获取和保存。以下是具体的实现步骤和代码示例。 环境准备 在开始之前,请确保您的工作环境中已…...

字节数组输出流转换为Base64方法记录
1. 今天在做字节数组转换Base64的时候遇到一个问题,转换成的Base64字符串自动换行,导致传输失败 关键代码: ByteArrayOutputStream out new ByteArrayOutputStream(); ............. BASE64Encoder encoder new BASE64Encoder(); Stri…...
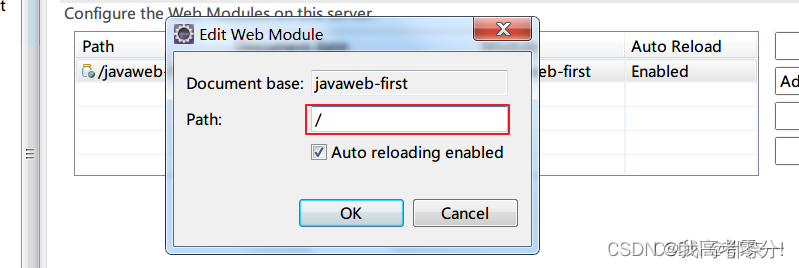
在eclipse中导入idea项目步骤
一、可以把其它项目的.project, .classpath文件拷贝过来,修改相应的地方则可。 1、.project文件只需要修改<name>xxx</name>这个项目名称则可 2、.classpath文件通常不用改, 二、右击 项目名 >选择“Properties”>选择 Re…...
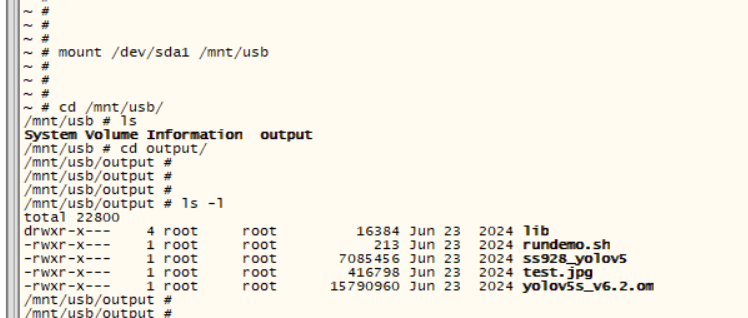
海思SS928/SD3403开发笔记4——u盘挂载
首先一定要将u盘格式化成fat32。 挂载 mkdir /mnt/usb mount /dev/sda1 /mnt/usb成功示意图: 取消挂载 umount /mnt/usb...
)
偏微分方程算法之抛物型方程差分格式编程示例六(混合边界条件下C-N格式)
目录 一、研究问题 二、C++代码 三、计算结果 一、研究问题 对于混合边界条件下的抛物型偏微分方程求解,我们使用Crank-Nicolson格式(C-N格式),边界条件采用中心差商,即...

【5G核心网】5G NWDAF(Network Data Analytics Function)网元功能介绍
博主未授权任何人或组织机构转载博主任何原创文章,感谢各位对原创的支持! 博主链接 本人就职于国际知名终端厂商,负责modem芯片研发。 在5G早期负责终端数据业务层、核心网相关的开发工作,目前牵头6G技术研究。 博客内容主要围绕…...

今日思考分享:全网爆火的山东车牌之歌原因是什么?
山东车牌之歌的爆火反映了一种潜在而又浅显的需求被满足的过程。 首先,这首歌击中了人们的“潜”需求。在日常出行中,我们确实会偶尔对看到的不同地区车牌产生好奇,但往往这种好奇心一闪而过,没有具体的途径去满足。而山东车牌之歌…...

Spring Boot 2.x + Mybatis Plus 多数据源配置
MP官方文档提供有多数据源配置方案,这里没有使用其方案,原因是项目不想引入过多依赖 提供一下官网的文档供各位选择多数据源支持 | MyBatis-Plus (baomidou.com) 配置文件 application.properties文件配置两个数据源信息,yaml文件自行修改…...

2、数据库模型图、er图
关系 user和administarators是多对一的关系 user和order是一对多的关系 shipped和order是多对一的关系 order和books是多对多的关系 leavewords和order是一对一的关系 stock和books是一对多的关系 Chens 数据库表示法——ER图 Crows Foot数据库表示法——数据库模型图 Navicat表…...
Docker的理解
Docker的理解 Docker为什么用Docker?1.提升系统资源利用率2.更快速的交付和部署3.高效的部署和扩容4.更简单的管理 Docker核心技术Docker镜像Docker容器Docker仓库 Docker实现原理Linux NamespaceCgroupUnion FS Docker的应用场景1.微服务架构2.持续集成3.快速部署和…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
