C语言一些逆置算法
目录
整数逆置
数组逆置
矩阵转置
整数逆置
如7234变为4327
int Reversed(int n){int x,reversed_n=0;while(n!=0){x=n%10; reversed_n=reversed_n*10+x;n=n/10;}return reversed_n;
}
数组逆置
将数组{1,2,3,4,5,6}逆置为{6,5,4,3,2,1}
void Reverse(int a[],int l,int r){while(l<r){int temp;temp=a[l];a[l]=a[r];a[r]=temp;l++;r--;}
}
利用数组逆置的性质,然后我们知道(A-1B-1)-1 = BA ,可以用这个性质实现循环左移函数
void Converse(int a[],int num,int len){ //num是移动位数,len是数组长度Reverse(a,0,num-1); //A逆Reverse(a,num,len-1); //B逆Reverse(a,0,len-1); //然后AB整体逆就能得到BA
}
//主函数
int a[8]={1,2,3,4,5,6,7,8};
Converse(a,3,8); //循环左移三位
矩阵转置
以对角线为对称交换两个元素
int temp;
for (i = 0; i < n; i++) { //两个for循环遍历上三角元素for (j = i + 1; j < n; j++) { //上三角与下三角交换temp = a[i][j];a[i][j] = a[j][i]; a[j][i] = temp;}
}
相关文章:

C语言一些逆置算法
目录 整数逆置 数组逆置 矩阵转置 整数逆置 如7234变为4327 int Reversed(int n){int x,reversed_n0;while(n!0){xn%10; reversed_nreversed_n*10x;nn/10;}return reversed_n; }数组逆置 将数组{1,2,3,4,5,6}逆置为{6,5,4,3,2,1} void Reverse(int a[],int l,int r){w…...

CentOS7安装MongoDB
文章目录 一、 环境准备二、安装包下载三、 软件安装和启动3.1 将下载好的安装包上传到 Linux 服务器某个目录下,并使用以下命令解压压缩包。3.2 将解压后的目录移动到 /usr/local 目录下,并改名为 mongodb 。3.3 进入 mongo 目录,并创建文件…...

python笔记----少儿编程课程
第1课: 认识新朋友-python 知识点: 1、在英文状态下编写Python语句。 2、内置函数print()将结果输出到标准的控制台上,它的基本语法格式如下: print("即将输出的内容") #输出的内容要用引号引起来,可…...
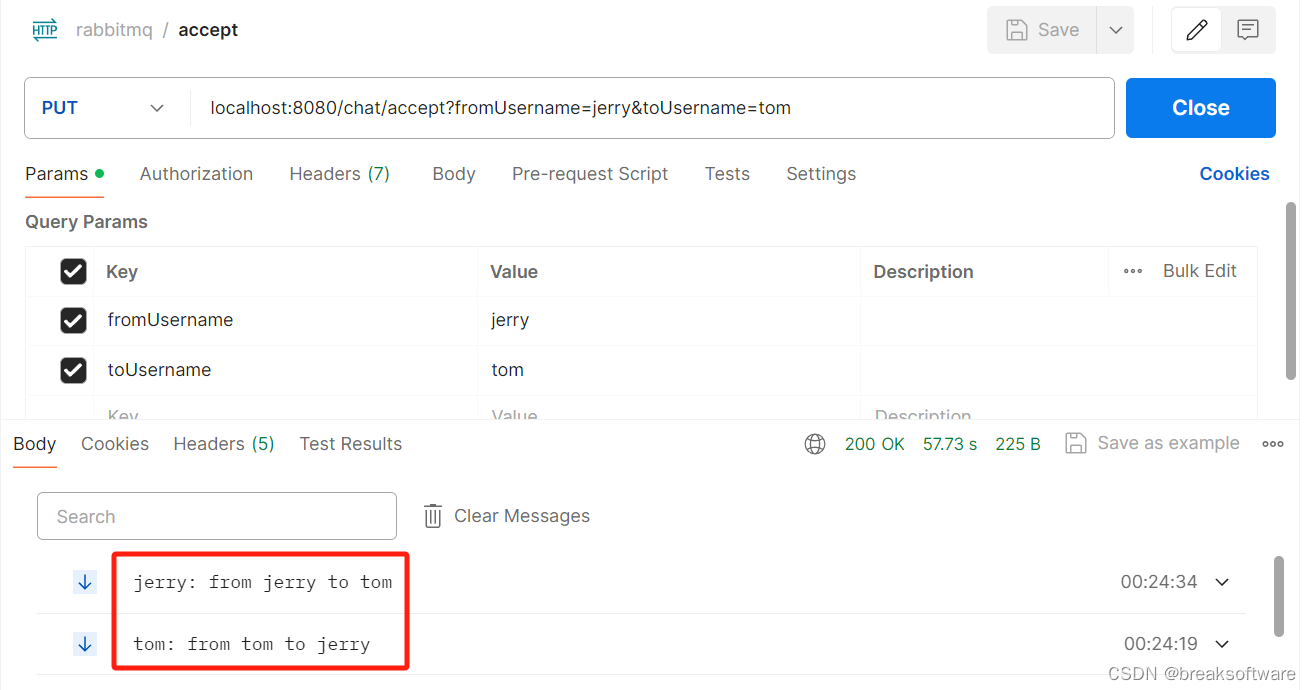
RabbitMQ实践——搭建单人聊天服务
大纲 创建Core交换器用户登录发起聊天邀请接受邀请聊天实验过程总结代码工程 经过之前的若干节的学习,我们基本掌握了Rabbitmq各个组件和功能。本文我们将使用之前的知识搭建一个简单的单人聊天服务。 基本结构如下。为了避免Server有太多连线导致杂乱,下…...

GPT-5
欢迎来到 Papicatch的博客 文章目录 🍉技术突破预测 🍈算法进步 🍈理解力提升 🍈行业推动力 🍉人机协作的未来 🍈辅助决策 🍈增强创造力 🍈复杂任务中的角色 🍈人…...
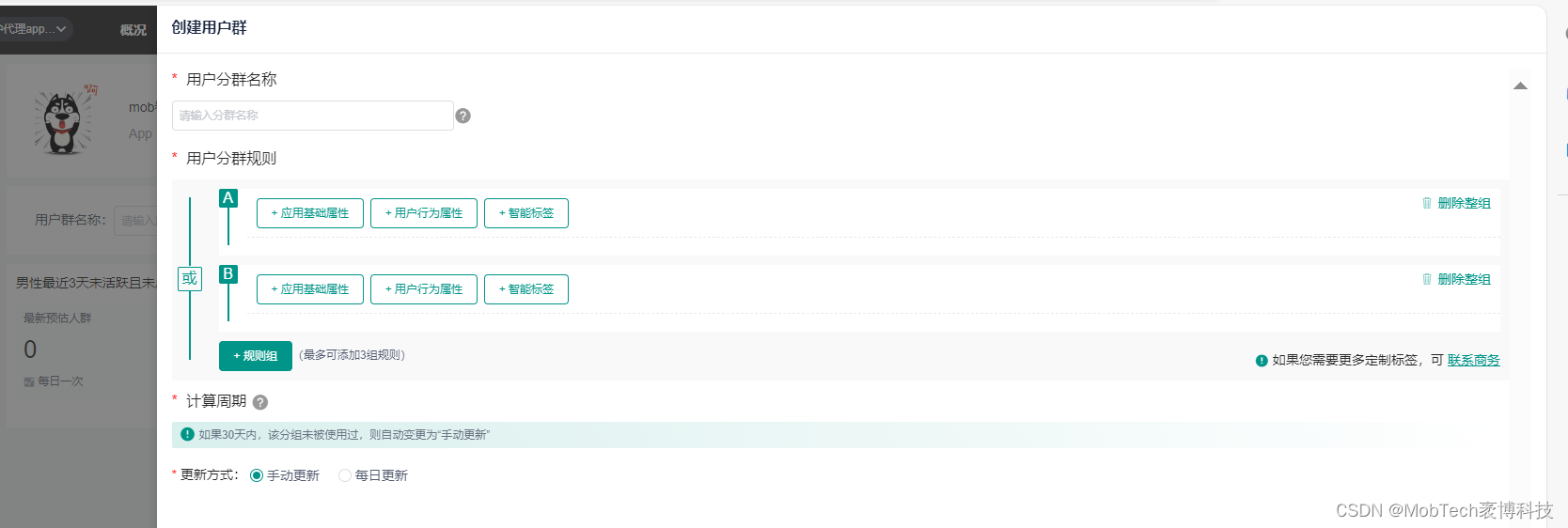
Vip-智能预估+大数据标签+人群全选=用户分群!
Mobpush用户分群功能升级,创建推送入口vip用户可进入自有选择标签创建“用户分群”,相比于免费标签,“用户标签”维度更丰富。在应用基础属性上,增加“品牌”、“网络状态”、“运营商”,众所周知,不同厂商…...
SpringBoot异常处理机制之自定义404、500错误提示页面 - 518篇
历史文章(文章累计500) 《国内最全的Spring Boot系列之一》 《国内最全的Spring Boot系列之二》 《国内最全的Spring Boot系列之三》 《国内最全的Spring Boot系列之四》 《国内最全的Spring Boot系列之五》 《国内最全的Spring Boot系列之六》 《…...

为什么选择Xinstall CPA结算系统?因为它能帮您解决这些痛点!
在App推广和运营的道路上,我们时常面临着各种挑战和痛点。其中,结算系统的复杂性和不透明性往往成为制约我们发展的瓶颈。然而,有了Xinstall CPA结算系统,这些问题将迎刃而解,让您的App推广之路更加顺畅和高效。 一、…...

2024年【建筑电工(建筑特殊工种)】模拟试题及建筑电工(建筑特殊工种)作业考试题库
题库来源:安全生产模拟考试一点通公众号小程序 2024年建筑电工(建筑特殊工种)模拟试题为正在备考建筑电工(建筑特殊工种)操作证的学员准备的理论考试专题,每个月更新的建筑电工(建筑特殊工种)作业考试题库祝您顺利通过建筑电工(建筑特殊工种)考试。 1、…...

解锁数字化转型的双引擎:MSP和CMP的力量
随着企业数字化转型的深入,云计算已经成为现代企业IT基础设施的重要组成部分。为了高效地管理和优化多云环境,企业通常会依赖管理服务提供商 (Managed Service Providers, MSP) 和云管理平台 (Cloud Management Platforms, CMP)。本文将探讨MSP和CMP的定…...
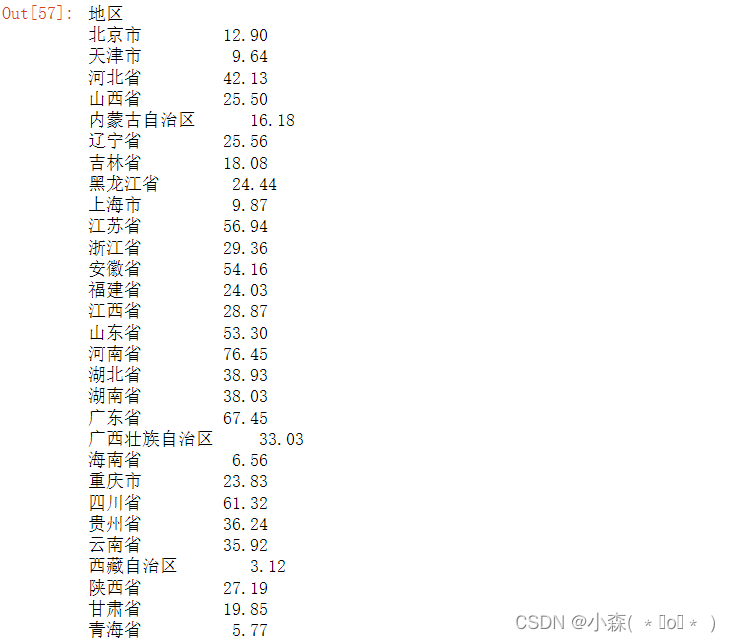
Pyecharts入门
数据可视化 Pyecharts简介 Apache ECharts 是一个由百度开源的数据可视化,凭借着良好的交互性,精巧的图表设计,得到了众多开发者的认可。而 Python 是一门富有表达力的语言,很适合用于数据处理。当数据分析遇上数据可视化时&#…...
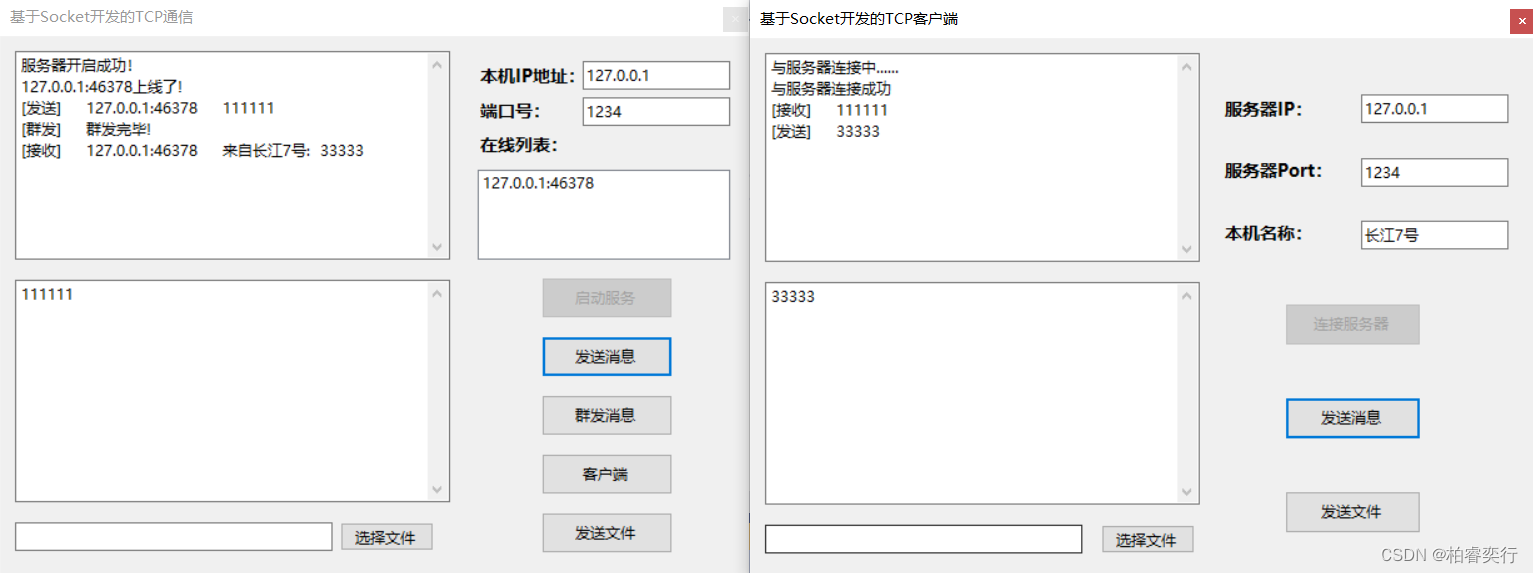
Socket编程详解(一)服务端与客户端的双向对话
目录 预备知识 视频教程 项目前准备知识点 1、服务器端程序的编写步骤 2、客户端程序编写步骤 代码部分 1、服务端FrmServer.cs文件 2、客户端FrmClient.cs文件 3、启动文件Program.cs 结果展示 预备知识 请查阅博客http://t.csdnimg.cn/jE4Tp 视频教程 链接&#…...
)
使用Python实现深度学习模型:强化学习与深度Q网络(DQN)
深度Q网络(Deep Q-Network,DQN)是结合深度学习与强化学习的一种方法,用于解决复杂的决策问题。本文将详细介绍如何使用Python实现DQN,主要包括以下几个方面: 强化学习简介DQN算法简介环境搭建DQN模型实现模型训练与评估1. 强化学习简介 强化学习是一种训练智能体(agent…...

Py-Spy、Scalene 和 VizTracer 的对比分析
在前几篇文章中,我们详细介绍了如何使用 py-spy、scalene 和 viztracer 进行性能分析和优化。今天,我们将对这三个性能分析工具进行详细对比,帮助你选择最适合你的工具。 工具简介 Py-Spy: 实时性能分析:Py-Spy 可以…...

软考架构师考试内容
软考系统架构设计师考试是中国计算机技术与软件专业技术资格(水平)考试(简称软考)中的一项高级资格考试,旨在评估考生是否具备系统架构设计的能力。根据提供的参考资料,考试内容主要包括以下几个方面&#…...

【MySQL基础篇】概述及SQL指令:DDL及DML
数据库是一个按照数据结构来组织、存储和管理数据的仓库。以下是对数据库概念的详细解释:定义与基本概念: 数据库是长期存储在计算机内的、有组织的、可共享的、统一管理的大量数据的集合。 数据库不仅仅是数据的简单堆积,而是遵循一定的规则…...
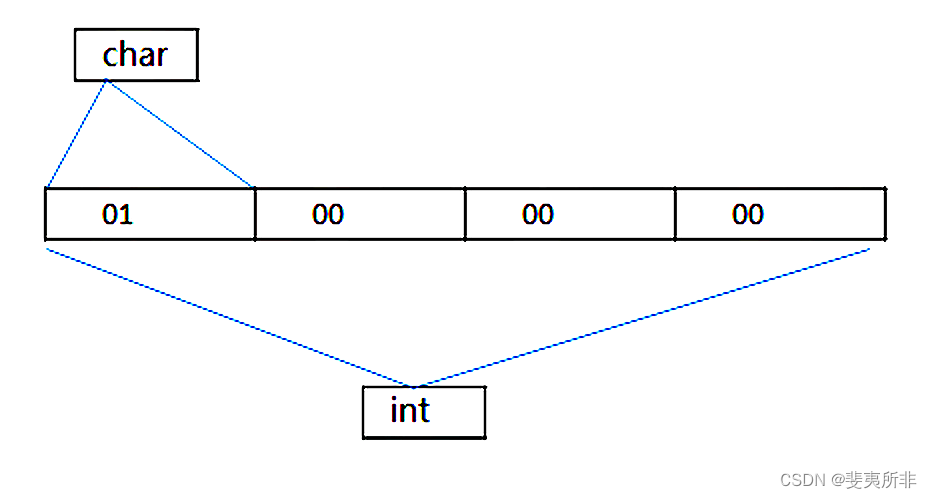
计算机网络 —— 网络字节序
网络字节序 1、网络字节序 (Network Byte Order)和本机转换 1、大端、小端字节序 “大端” 和” 小端” 表示多字节值的哪一端存储在该值的起始地址处;小端存储在起始地址处,即是小端字节序;大端存储在起始地址处,即是大端字节…...

区块链不可能三角
区块链不可能三角:探索去中心化、安全与可扩展性的权衡 引言 区块链技术自诞生以来,以其去中心化、透明、安全等特点吸引了全球的关注,成为金融科技领域的重要革新力量。然而,随着区块链应用的日益广泛,一个核心问题…...
新手第一个漏洞复现:MS17-010(永恒之蓝)
文章目录 漏洞原理漏洞影响范围复现环境复现步骤 漏洞原理 漏洞出现在Windows SMB v1中的内核态函数srv!SrvOs2FeaListToNt在处理FEA(File Extended Attributes)转换时。该函数在将FEA list转换成NTFEA(Windows NT FEA)list前&am…...

代码随想录Day64
98.所有可达路径 题目:98. 所有可达路径 (kamacoder.com) 思路:果断放弃 答案 import java.util.*;public class Main {private static List<List<Integer>> adjList;private static List<List<Integer>> allPaths;private sta…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...
