java二叉排序树
1.先看一个需求
给你一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加
2.解决方案分析
使用数组
数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢. [示意图]
数组排序,优点:可以使用二分查找,查找速度快,缺点:为了保证数组有序,在添加新数据时,找到插入位
置后,后面的数据需整体移动,速度慢。[示意图]
使用链式存储-链表
不管链表是否有序,查找速度都慢,添加数据速度比数组快,不需要数据整体移动。[示意图]
使用二叉排序树
3.二叉排序树介绍
二叉排序树:BST: (Binary Sort(Search) Tree), 对于二叉排序树的任何一个非叶子节点,要求左子节点的值比当
前节点的值小,右子节点的值比当前节点的值大。
特别说明:如果有相同的值,可以将该节点放在左子节点或右子节点
比如针对前面的数据 (7, 3, 10, 12, 5, 1, 9) ,对应的二叉排序树为
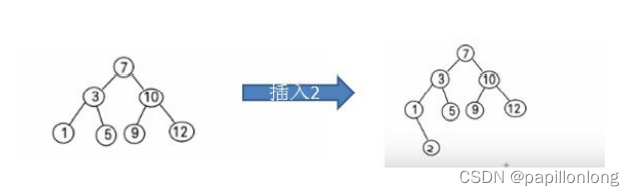
4.二叉排序树创建和遍历
一个数组创建成对应的二叉排序树,并使用中序遍历二叉排序树,比如: 数组为 Array(7, 3, 10, 12, 5, 1, 9) , 创
建成对应的二叉排序树为 :

5.二叉排序树的删除
二叉排序树的删除情况比较复杂,有下面三种情况需要考虑
- 删除叶子节点 (比如:2, 5, 9, 12)
- 删除只有一颗子树的节点 (比如:1)
- 删除有两颗子树的节点. (比如:7, 3,10 )
- 操作的思路分析
//对删除结点的各种情况的思路分析:
第一种情况:
删除叶子节点 (比如:2, 5, 9, 12)
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的 父结点 parent
(3) 确定 targetNode 是 parent 的左子结点 还是右子结点
(4) 根据前面的情况来对应删除
左子结点 parent.left = null
右子结点 parent.right = null;
第二种情况: 删除只有一颗子树的节点 比如 1
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的 父结点 parent
(3) 确定 targetNode 的子结点是左子结点还是右子结点
(4) targetNode 是 parent 的左子结点还是右子结点
(5) 如果 targetNode 有左子结点
5. 1 如果 targetNode 是 parent 的左子结点
parent.left = targetNode.left;
5.2 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.left;
(6) 如果 targetNode 有右子结点
6.1 如果 targetNode 是 parent 的左子结点
parent.left = targetNode.right;
6.2 如果 targetNode 是 parent 的右子结点
parent.right = targetNode.right
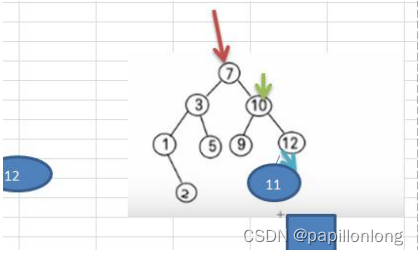
情况三 : 删除有两颗子树的节点. (比如:7, 3,10 )
思路
(1) 需求先去找到要删除的结点 targetNode
(2) 找到 targetNode 的 父结点 parent
(3) 从 targetNode 的右子树找到最小的结点
(4) 用一个临时变量,将 最小结点的值保存 temp = 11
(5) 删除该最小结点
(6) targetNode.value = temp
6.二叉排序树删除结点的代码实现:
public class BinarySortTreeDemo {public static void main(String[] args) {// TODO Auto-generated method stubint arr[] = { 7, 3, 10, 12, 5, 1, 9, 2 };BinarySortTree binarySortTree = new BinarySortTree();// 循环的添加结点到二叉树for (int i = 0; i < arr.length; i++) {binarySortTree.add(new Node(arr[i]));}// 中序遍历二叉排序树System.out.println("中序遍历二叉排序树");binarySortTree.infixOrder();// 1,3,5,7,9,10,12// 测试一下删除叶子节点
// binarySortTree.delNode(2);
// binarySortTree.delNode(1);binarySortTree.delNode(7);System.out.println("删除结点后");binarySortTree.infixOrder();}}//创建二叉排序树
class BinarySortTree {private Node root;// 查找要删除的结点public Node search(int value) {if (root == null) {return null;} else {return root.search(value);}}// 查找父结点public Node searchParent(int value) {if (root == null) {return null;} else {return root.searchParent(value);}}// 编写方法// 1.返回以node为根节点的二叉排序树的最小节点的值// 2.删除以node为根节点的二叉排序树的最小节点的值/*** * @param node 传入的结点(当作二叉排序树的根节点)* @return 返回的以node为结点的二叉树的最小结点的值*/public int delRightTreeMin(Node node) {Node target = node;// 循环的查找左节点,就会找到最小值while (target.left != null) {target = target.left;}// 这时target就指向了最小节点// 删除最小节点delNode(target.value);return target.value;}// 删除结点public void delNode(int value) {if (root == null) {return;} else {// 1.需要先去找到要删除的结点 targetNodeNode targetNode = search(value);// 如果没有找到要删除的结点if (targetNode == null) {return;}// 如果我们发现targetNode没有父结点if (root.left == null && root.right == null) {root = null;return;}// 去查找targetNode的父结点Node parent = searchParent(value);// 如果要删除的节点是叶子节点if (targetNode.left == null && targetNode.right == null) {// 判断targetNode是父结点的左指结点还是右子节点if (parent.left != null && parent.left.value == value) {// 是左指结点parent.left = null;} else if (parent.right != null && parent.right.value == value) {// 是右子结点parent.right = null;}} else if (targetNode.left != null && targetNode.right != null) {// 删除有两颗子树的节点int minVal = delRightTreeMin(targetNode.right);targetNode.value = minVal;} else {// 删除只有一颗子树的结点// 如果要删除的结点有左指结点if (targetNode.left != null) {// 如果targetNode是parent的左指结点if (parent.left.value == value) {parent.left = targetNode.left;} else {// targetNode是parent的右子结点parent.right = targetNode.left;}} else {// 如果要删除的节点有右子结点// 如果targetNode是parent的左指结点if (parent.left.value == value) {parent.left = targetNode.right;} else {// 如果targetNode是parent的右指结点parent.right = targetNode.right;}}}}}// 添加结点方法public void add(Node node) {if (root == null) {root = node;// 如果root为空则直接让root指向node} else {root.add(node);}}// 中序遍历public void infixOrder() {if (root != null) {root.infixOrder();} else {System.out.println("二叉排序树为空,不能遍历");}}
}//创建Node结点
class Node {int value;Node left;Node right;public Node(int value) {super();this.value = value;}// 查找要删除的结点/*** * @param value 希望删除的结点的值* @return 如果找到返回该节点,否则返回null*/public Node search(int value) {if (value == this.value) {return this;} else if (value < this.value) {// 如果查找的值小于当前节点,向左子树递归查找// 如果左子结点为空if (this.left == null) {return null;}return this.left.search(value);} else {// 如果查找的值不小于当前节点,向右子树递归查找if (this.right == null) {return null;}return this.right.search(value);}}// 查找要删除该节点的父节点/*** * @param value 要找到的结点的值* @return 返回的是要删除的结点的父节点,如果没有就返回null*/public Node searchParent(int value) {// 如果当前结点就是要删除的结点的父结点,就返回if ((this.left != null && this.left.value == value) || (this.right != null && this.right.value == value)) {return this;} else {// 如果要查找的值小于当前节点的值,并且当前节点的左指结点不为空if (value < this.value && this.left != null) {return this.left.searchParent(value);// 向左子树递归查找} else if (value >= this.value && this.right != null) {return this.right.searchParent(value);// 向右子树递归查找} else {return null;// 没有找到父结点}}}@Overridepublic String toString() {return "Node [value=" + value + "]";}// 添加结点方法// 递归的方式添加结点,需要满足二叉排序树的要求public void add(Node node) {if (node == null) {return;}// 判断传入结点的值,和当前子树的根结点的值关系if (node.value < this.value) {// 如果当前节点左子节点为nullif (this.left == null) {this.left = node;} else {// 递归的向左子树添加this.left.add(node);}} else {// 添加的结点的值大于当前节点的值if (this.right == null) {this.right = node;} else {// 递归向右子树添加this.right.add(node);}}}// 中序遍历public void infixOrder() {if (this.left != null) {this.left.infixOrder();}System.out.println(this);if (this.right != null) {this.right.infixOrder();}}
}
相关文章:

java二叉排序树
1.先看一个需求 给你一个数列 (7, 3, 10, 12, 5, 1, 9),要求能够高效的完成对数据的查询和添加 2.解决方案分析 使用数组 数组未排序, 优点:直接在数组尾添加,速度快。 缺点:查找速度慢. [示意图] 数组排序…...

聊一聊 gRPC 的四种通信模式
温馨提示:本文需要结合上一篇 gRPC 文章一起食用,否则可能看不懂。 前面一篇文章松哥和大家聊了 gRPC 的基本用法,今天我们再来稍微深入一点点,来看下 gRPC 中四种不同的通信模式。 gRPC 中四种不同的通信模式分别是:…...

科技云报道:开源真的香,风险知多少?
科技云报道原创。 过去几年,开源界一片火热,开源软件技术已全面进军操作系统、云原生、人工智能、大数据、半导体、物联网等行业领域。 数据显示,我国超九成企业在使用或正计划使用开源技术。 与此同时,全球各大开源组织相继兴…...

国产化适配迁移记录
国产化适配迁移记录 本项目基于RuoYi-Vue的框架进行迁移。目前已完成覆盖测试暂无其他问题。 国产化环境 名称版本达梦数据库DmJdbcDriver18 8.1.2.144通用mapper – tk.mybatismapper-spring-boot-starter 4.2.5<!-- 达梦数据库--><dependency><groupId>…...

又一国产开源项目走向世界,百度RPC框架Apache bRPC正式成为ASF顶级项目
2023 年 1 月 26 日,Apache 软件基金会 (ASF) 官方正式宣布Apache bRPC 正式毕业,成为 Apache的顶级项目。 我听到这个消息是挺开心的,毕竟是又一款由国人主导的apche顶级项目,再次证明国内在开源界正在发挥越来越重要的作用。 …...

多数据库学习之GBase8s查询数据库表元信息常用SQL
多数据库学习之GBase8s查询数据库表元信息常用SQL简介常用SQL创建用户创建数据库及模式获取表元数据其他参考链接简介 背景介绍 GBase 8t是基于IBM informix源代码、编译和测试体系自主研发的交易型数据库产品。 南大通用安全数据库管理系统(简称 GBase 8sÿ…...

Jetpack之Lifecycle应用与源码分析
Build lifecycle-aware components that can adjust behavior based on the current lifecycle state of an activity or fragment. 上面是源于官网的定义,简单翻译就是说Lifecycle的作用就是基于当前的Activity或者Fragment的生命周期当前状态构建可感知生命周期的…...

Python序列类型之集合
💐💐💐欢迎来到小十一的博客!!! 🎯博客主页:🎯程序员小十一的博客 🚀博客专栏:🚀Python入门基础语法 🌷欢迎关注ÿ…...

java 自定义json解析注解 复杂json解析
java 自定义json解析注解 复杂json解析 工具类 目录java 自定义json解析注解 复杂json解析 工具类1.背景2、需求-各式各样的json一、一星难度json【json对象中不分层】二、二星难度json【json对象中出现层级】三、三星难度json【json对象中存在数组】四、四星难度json【json对象…...

Vue3配置路由(vue-router)
文章目录前言一、配置路由(vue-router)1、安装路由2、新建页面3、创建路由配置文件4.特殊报错!前言 紧接上篇文章,vue3的配置与vue2是有所差别的,本文就讲述了如何配置,如果本文对你有所帮助请三连支持博主…...

【代码随想录二刷】Day9-字符串-C++
代码随想录二刷Day9 今日任务 28.找出字符串中第一个匹配项的下标 459.重复的子字符串 字符串总结 双指针总结 语言:C KMP 链接:https://programmercarl.com/0459.重复的子字符串.html#kmp 用处:当出现字符串不匹配时,可以利…...

google colab上如何下载bert相关模型
首先要知道模型的地址 tensorflow版本的模型: https://storage.googleapis.com/bert_models/2018_10_18/cased_L-12_H-768_A-12.zip https://storage.googleapis.com/bert_models/2018_11_03/chinese_L-12_H-768_A-12.zip pytorch版本的模型 ‘bert-base-cased’: …...
Vue2.0页面缓存机制联合页面标签的交互(keep-alive + router)
预期效果:(借助iview-ui的在线体验页面示意一下) 项目中只有一部分页面需要缓存,且存在多级路由的页面。每打开一个菜单,就会新增一个 Tab标签,只要 Tab标签不关闭,对应的页面就会被缓存&#x…...
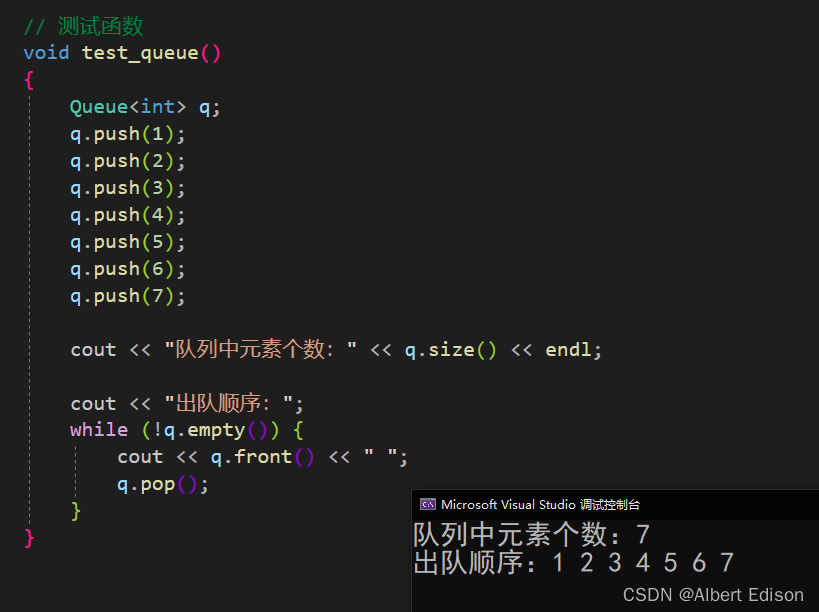
C++STL剖析(四)—— stack和queue的概念和使用
文章目录1. stack的介绍2. stack的构造3. stack的使用🍑 push🍑 top🍑 pop🍑 empty🍑 size🍑 swap🍑 emplace4. queue的介绍5. queue的构造6. queue的使用🍑 push🍑 size…...

流浪地球 | 建筑人是如何看待小破球里的黑科技的?
大家好,这里是建模助手。 想问问大家今年贺岁档,都跟上没有,今天请允许我蹭一下热点表达一下作为一个科幻迷的爱国之情。 抛开大刘的想象力、各种硬核科技&以及大国情怀不提,破球2中的传承还是让小编很受感动,无…...
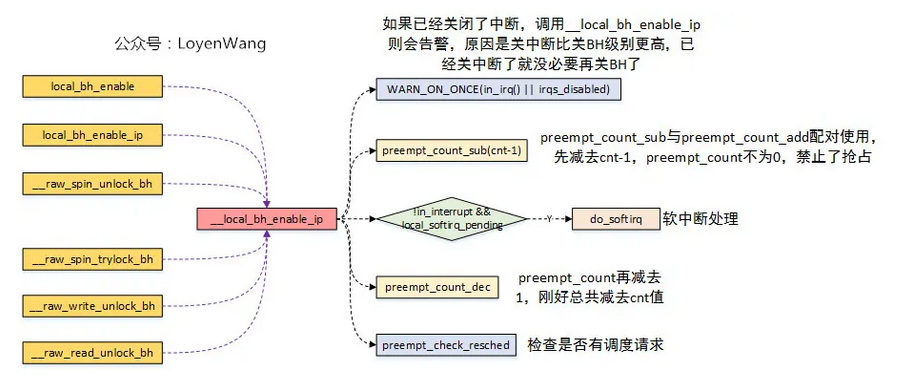
软中断在bottom-half中调用
https://www.bilibili.com/read/cv20785285/简介软中断可以在两个位置得到机会执行:硬中断返回前 irq_exit中断下半部 Bottom-half Enable后情景分析情景1spin_unlock_bh__raw_spin_unlock_bh__local_bh_enable_ip 打开Bottom-half,并让softirq有机会…...
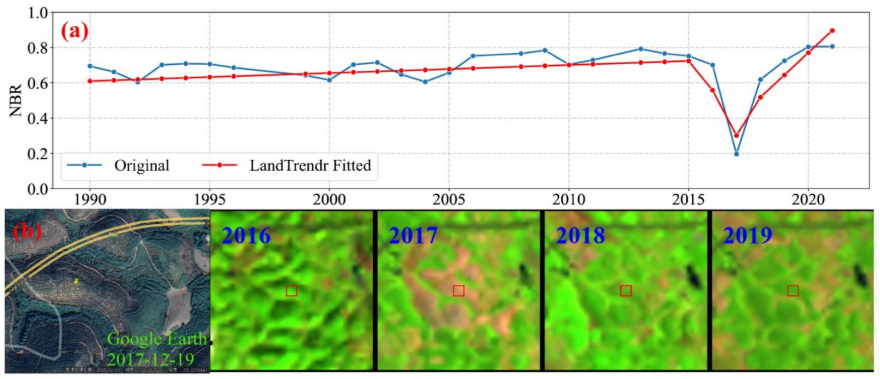
GEE遥感云大数据在林业中的应用
近年来遥感技术得到了突飞猛进的发展,航天、航空、临近空间等多遥感平台不断增加,数据的空间、时间、光谱分辨率不断提高,数据量猛增,遥感数据已经越来越具有大数据特征。遥感大数据的出现为相关研究提供了前所未有的机遇…...

Apollo架构篇 - 客户端架构
前言 本文基于 Apollo 1.8.0 版本展开分析。 客户端 使用 Apollo 支持 API 方式和 Spring 整合两种方式。 API 方式 API 方式是最简单、高效使用使用 Apollo 配置的方式,不依赖 Spring 框架即可使用。 获取命名空间的配置 // 1、获取默认的命名空间的配置 C…...
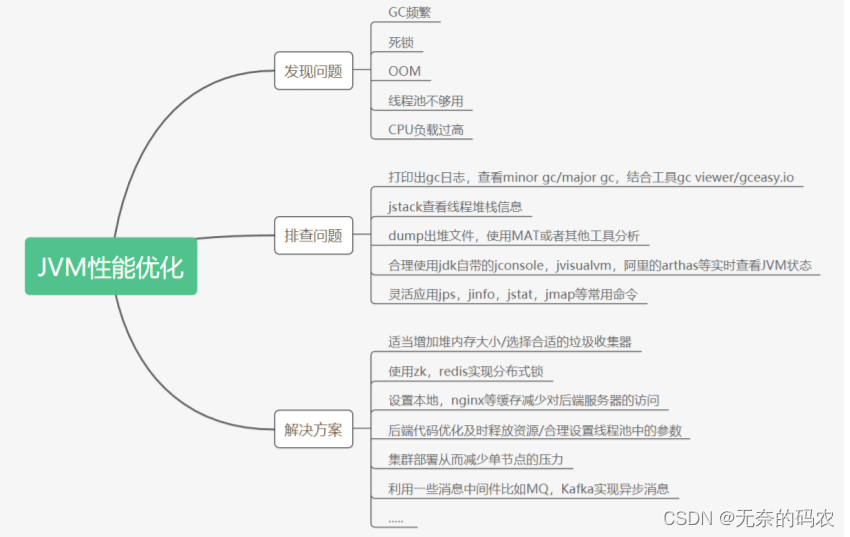
JVM调优最全面的成长 :参数详解+垃圾算法+示例展示+类文件到源码+面试问题
目录1.优秀的Java开发者1.1 什么是Java?1.2 编程语言1.3 计算机[硬件]能够懂的语言1.3.1 计算机发展史1.3.2 计算机体系结构1.3.3 计算机处理数据过程1.3.4 机器语言1.3.5 不同厂商的CPU1.3.6 操作系统1.3.7 汇编语言1.3.8 高级语言1.3.9 编译型和解释型1.3.9.1 编译…...

linux驱动常用函数
以下为一些常见用户态函数在内核中的替代,包括头文件和函数声明:1、动态申请内存:linux/vmalloc.hvoid *vmalloc(unsigned long size);void vfree(const void *addr);2、字符串操作:linux/string.hvoid * memset(void *,int,__ker…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...
