数据结构之B树:深入了解与应用
目录
1. B树的基本概念
1.1 B树的定义
1.2 B树的性质
1.3 B树的阶
2. B树的结构
2.1 节点结构
2.2 节点分裂
2.3 节点合并
3. B树的基本操作
3.1 搜索
3.2 插入
3.3 删除
4. B树的应用
4.1 数据库索引
4.2 文件系统
4.3 内存管理
5. B树的优势和局限
5.1 优势
5.2 局限
6. B树的实现与示例
6.1 B树的插入操作示例
6.2 B树的搜索操作示例
6.3 B树的删除操作示例
7. 结论
B树(B-Tree)是一种自平衡的树数据结构,广泛应用于数据库和文件系统中,用于高效地执行插入、删除和搜索操作。本文将详细介绍B树的概念、结构、操作及其应用,并通过实例和图示帮助读者深入理解B树的工作原理和优势。
1. B树的基本概念
1.1 B树的定义
B树是一种平衡多路查找树,具有以下特点:
- 每个节点包含多个关键字(Keys)和子节点(Children)。
- 节点中的关键字按升序排列。
- 每个节点的子节点数量与其关键字数量有严格关系:假设一个节点包含 n 个关键字,那么它必须有 n+1 个子节点。
- 所有叶子节点在同一层次上,保证了树的平衡性。
1.2 B树的性质
B树的性质包括:
- 根节点至少有两个子节点(除非是空树)。
- 每个节点最多有 m 个子节点(m 是B树的阶,m >= 2)。
- 每个节点(除根节点和叶子节点)至少有 ⌈m/2⌉ 个子节点。
- 所有叶子节点都在同一层次上。
1.3 B树的阶
B树的阶(Order)是一个关键参数,表示每个节点的最大子节点数量。常见的B树阶包括B-Tree、B+-Tree、B*-Tree等,具体的结构和操作可能略有不同,但基本思想是一致的。
2. B树的结构
2.1 节点结构
每个节点包含以下部分:
- 关键字数组(Keys):按升序排列的关键字列表。
- 子节点指针数组(Children):指向子节点的指针列表,数量比关键字多1。
- 节点属性(Properties):包括当前关键字数量、是否为叶子节点等。
2.2 节点分裂
当节点中的关键字数量达到最大值时,需要进行分裂操作,将节点分为两个部分,并将中间关键字提升到父节点中。这个过程保证了B树的平衡性。
2.3 节点合并
当节点中的关键字数量低于最小值时,需要进行合并操作,将关键字和子节点与相邻节点合并,以维持B树的平衡性。
3. B树的基本操作
3.1 搜索
B树的搜索操作类似于二分查找,按以下步骤进行:
- 从根节点开始,逐个比较关键字,找到目标关键字或确定目标关键字所在的子节点。
- 递归地在子节点中搜索,直到找到目标关键字或到达叶子节点。
3.2 插入
B树的插入操作包括以下步骤:
- 从根节点开始,找到插入位置的叶子节点。
- 将新关键字插入叶子节点,保持关键字的升序排列。
- 如果节点关键字数量超过最大值,进行节点分裂,并将中间关键字提升到父节点。
- 递归处理分裂的父节点,直到树恢复平衡。
3.3 删除
B树的删除操作相对复杂,包括以下步骤:
- 找到要删除的关键字所在的节点。
- 如果关键字在叶子节点中,直接删除。
- 如果关键字在内部节点中,用前驱或后继关键字替换,并在子树中删除前驱或后继关键字。
- 如果节点关键字数量低于最小值,进行节点合并或关键字重分配,保持树的平衡性。
4. B树的应用
4.1 数据库索引
B树广泛应用于数据库索引中,如B-Tree索引、B+-Tree索引等。B树结构保证了索引的平衡性和高效性,支持快速插入、删除和搜索操作,适用于大规模数据管理。
4.2 文件系统
B树也应用于文件系统中,如NTFS和HFS+等。通过B树结构,可以高效管理文件目录和元数据,实现快速文件访问和操作。
4.3 内存管理
在内存管理中,B树用于实现分页和虚拟内存映射,通过高效的查找和管理算法,优化内存分配和访问性能。
5. B树的优势和局限
5.1 优势
- 平衡性: B树的所有叶子节点在同一层次上,保证了树的平衡性。
- 高效性: B树的搜索、插入和删除操作都在O(log n)时间复杂度内完成,适合大规模数据管理。
- 灵活性: B树支持多种阶和变种(如B+-Tree、B*-Tree等),可以根据具体应用需求调整结构和参数。
5.2 局限
- 空间复杂度: B树需要额外的指针和属性存储,可能增加内存开销。
- 节点分裂和合并: 插入和删除操作可能涉及节点分裂和合并,增加了操作复杂度和开销。
6. B树的实现与示例
6.1 B树的插入操作示例
以下是一个B树插入操作的示例,演示了插入关键字和节点分裂的过程:
class BTreeNode:def __init__(self, leaf=False):self.leaf = leafself.keys = []self.children = []class BTree:def __init__(self, t):self.root = BTreeNode(True)self.t = t # 最小度数def insert(self, key):root = self.rootif len(root.keys) == 2 * self.t - 1:temp = BTreeNode()self.root = temptemp.children.insert(0, root)self._split_child(temp, 0)self._insert_non_full(temp, key)else:self._insert_non_full(root, key)def _split_child(self, node, i):t = self.ty = node.children[i]z = BTreeNode(y.leaf)node.children.insert(i + 1, z)node.keys.insert(i, y.keys[t - 1])z.keys = y.keys[t: (2 * t - 1)]y.keys = y.keys[0: (t - 1)]if not y.leaf:z.children = y.children[t: (2 * t)]y.children = y.children[0: (t - 1)]def _insert_non_full(self, node, key):i = len(node.keys) - 1if node.leaf:node.keys.append(0)while i >= 0 and key < node.keys[i]:node.keys[i + 1] = node.keys[i]i -= 1node.keys[i + 1] = keyelse:while i >= 0 and key < node.keys[i]:i -= 1i += 1if len(node.children[i].keys) == 2 * self.t - 1:self._split_child(node, i)if key > node.keys[i]:i += 1self._insert_non_full(node.children[i], key)
6.2 B树的搜索操作示例
以下是一个B树搜索操作的示例,演示了在B树中查找关键字的过程:
def search(self, node, key):i = 0while i < len(node.keys) and key > node.keys[i]:i += 1if i < len(node.keys) and key == node.keys[i]:return (node, i)elif node.leaf:return Noneelse:return self.search(node.children[i], key)
6.3 B树的删除操作示例
以下是一个B树删除操作的示例,演示了在B树中删除关键字的过程:
def delete(self, key):self._delete(self.root, key)if len(self.root.keys) == 0:if not self.root.leaf:self.root = self.root.children[0]else:self.root = BTreeNode(True)def _delete(self, node, key):t = self.ti = 0while i < len(node.keys) and key > node.keys[i]:i += 1if i < len(node.keys) and key == node.keys[i]:if node.leaf:node.keys.pop(i)else:self._delete_internal_node(node, key, i)elif node.leaf:returnelse:self._delete(node.children[i], key)if len(node.children[i].keys) < t - 1:self._fix(node, i)def _delete_internal_node(self, node, key, i):t = self.tif len(node.children[i].keys) >= t:pred = self._get_predecessor(node.children[i])node.keys[i] = predself._delete(node.children[i], pred)elif len(node.children[i + 1].keys) >= t:succ = self._get_successor(node.children[i + 1])node.keys[i] = succself._delete(node.children[i + 1], succ)else:self._merge(node, i)self._delete(node.children[i], key)def _get_predecessor(self, node):if node.leaf:return node.keys[-1]else:return self._get_predecessor(node.children[-1])def _get_successor(self, node):if node.leaf:return node.keys[0]else:return self._get_successor(node.children[0])def _merge(self, node, i):child = node.children[i]sibling = node.children[i + 1]child.keys.append(node.keys.pop(i))child.keys.extend(sibling.keys)if not child.leaf:child.children.extend(sibling.children)node.children.pop(i + 1)def _fix(self, node, i):t = self.tif i != 0 and len(node.children[i - 1].keys) >= t:self._borrow_from_prev(node, i)elif i != len(node.children) - 1 and len(node.children[i + 1].keys) >= t:self._borrow_from_next(node, i)else:if i != len(node.children) - 1:self._merge(node, i)else:self._merge(node, i - 1)def _borrow_from_prev(self, node, i):child = node.children[i]sibling = node.children[i - 1]child.keys.insert(0, node.keys[i - 1])if not child.leaf:child.children.insert(0, sibling.children.pop())node.keys[i - 1] = sibling.keys.pop()def _borrow_from_next(self, node, i):child = node.children[i]sibling = node.children[i + 1]child.keys.append(node.keys[i])if not child.leaf:child.children.append(sibling.children.pop(0))node.keys[i] = sibling.keys.pop(0)
7. 结论
B树作为一种高效的多路查找树,广泛应用于数据库、文件系统和内存管理等领域。通过深入理解B树的结构和操作,读者可以更好地应用B树来优化数据管理和查询性能。本文详细介绍了B树的基本概念、结构、操作及其应用,并提供了具体的实现示例,帮助读者全面掌握B树的理论和实践。
相关文章:

数据结构之B树:深入了解与应用
目录 1. B树的基本概念 1.1 B树的定义 1.2 B树的性质 1.3 B树的阶 2. B树的结构 2.1 节点结构 2.2 节点分裂 2.3 节点合并 3. B树的基本操作 3.1 搜索 3.2 插入 3.3 删除 4. B树的应用 4.1 数据库索引 4.2 文件系统 4.3 内存管理 5. B树的优势和局限 5.1 优势…...
Tensorflow入门实战 T06-Vgg16 明星识别
目录 1、前言 2、 完整代码 3、运行过程结果 4、遇到的问题 5、小结 本文为🔗365天深度学习训练营 中的学习记录博客🍖 原作者:K同学啊 | 接辅导、项目定制 1、前言 这周主要是使用VGG16模型,完成明星照片识别。 2、 完整代…...

SpringBoot 3.3.1 + Minio 实现极速上传和预览模式
统一版本管理 <properties><minio.version>8.5.10</minio.version><aws.version>1.12.737</aws.version><hutool.version>5.8.28</hutool.version> </properties><!--minio --> <dependency><groupId>io.m…...

Linux: network: 丢包分析的另一个途径 tracing
丢包的另一个思路,内核里有些counter的计数,记录的不准确。这个时候怎么办?就需要使用另外一个方式:/sys/kernel/debug/tracing/event/skb/kfree_skb 的跟踪功能。这个算是对counter的一个补充,可以拿来做统计分析使用…...

【保姆级教程+配置源码】在VScode配置C/C++环境
目录 一、下载VScode 1. 在官网直接下载安装即可 2. 安装中文插件 二、下载C语言编译器MinGW-W64 三、配置编译器环境变量 1. 解压下载的压缩包,复制该文件夹下bin目录所在地址 2. 在电脑搜索环境变量并打开 3. 点击环境变量→选择系统变量里的Path→点击编…...
Qt creator实现一个简单计算器
目录 1 界面设计 2 思路简介 3 代码 目录 1 界面设计 2 思路简介 3 代码 3.1 widget.h 3.2 widget.c 4 完整代码 在这里主要记载了如何使用Qt creator完成一个计算器的功能。该计算器可以实现正常的加减乘除以及括号操作,能实现简单的计算器功能。 1 界…...

Java代码基础算法练习-计算被 3 或 5 整除数之和-2024.06.29
任务描述: 计算 1 到 n 之间能够被 3 或者 5 整除的数之和。 解决思路: 输入的数字为 for 循环总次数,每次循环就以当前的 i 进行 3、5 的取余操作,都成立计入总数sum中,循环结束,输出 sum 的值 代码示例&…...
核心代码讲解)
Socket编程详解(二)核心代码讲解
本文对代码的讲解基于上一篇博客 快速链接 Socket编程详解(一)服务端与客户端的双向对话 小试牛刀1:委托声明的关键字和委托方法使用的方法名是不一样的名称 可读性:有时,委托的名称可能描述了它的用途或它在哪里被…...

(项目实战)聚合支付系统开发环境搭建-基于VMware17安装Centos7.9
1 开发环境介绍 dtpay聚合支付系统和ecard预付卡系统,服务端部署在Linux环境。后续的开发环境,生产环境都是基于Linux进行搭建,系统使用到的相关中间件(RocketMQ,Redis,Nginx等),配置中心Nacos,数据库MySQ…...

Python现在可以在线编程了!
你好,我是郭震 1 在线编程 在线编程好处: 1 无需安装和配置环境: 在线编程平台不需要用户在本地安装任何软件或配置开发环境。这对初学者和那些希望快速上手进行编程的人非常有利。 2 跨平台兼容性: 这些平台可以在任何具有互联网连接的设备上使用&#…...

ThreadPoolExecutor线程池创建线程
线程池介绍 降低资源消耗。通过重复利用已创建的线程降低线程创建和销毁造成的消耗。提高响应速度。当任务到达时,任务可以不需要等到线程创建就能立即执行。提高线程的可管理性。线程是稀缺资源,如果无限制的创建,不仅会消耗系统资源&#…...

畅谈GPT-5
前言 ChatGBT(Chat Generative Bidirectional Transformer)是一种基于自然语言处理技术的对话系统,它的出现是人工智能和自然语言处理技术发展的必然趋势。随着技术的更新和进步,GPT也迎来了一代代的更新迭代。 1.GPT的回顾 1.1 GPT-3的介绍 GPT-3(Gen…...

石家庄高校大学智能制造实验室数字孪生可视化系统平台项目验收
智能制造作为未来制造业的发展方向,已成为各国竞相发展的重点领域。石家庄高校大学智能制造实验室积极响应国家发展战略,结合自身优势,决定引进数字孪生技术,构建一个集教学、科研、生产于一体的可视化系统平台。 数字孪生可视化…...

WLAN 4-Way Handshake如何生成GTK?
关于Wi-Fi的加密认证过程,可以参考如下链接,今天我们来理解如何生成GTK。 WLAN数据加密机制_tls加密wifi-CSDN博客 1 GTK GTK(Group Temporal Key)是由AP通过GMK生成,长度为128位,并在四次握手的第三步中…...

Qt/C++模拟鼠标键盘输入
1、控制鼠标移动 (1)Qt方案 QScreen* sc QGuiApplication::primaryScreen(); QCursor* c new QCursor(); int deltaX 10; int deltaY 10; c->setPos(sc, c->pos().x() deltaX, c->pos().y() deltaY);(2)Windows原…...
OpenGL3.3_C++_Windows(22)
材质: 决定物体在渲染过程中最终视觉呈现的关键因素之一,它通过一系列光学(投光物)和物理参数(反光度,反照率、金属度,折射率……)准确模拟现实世界中的材料特性,从而增…...
electron-builder 打包过慢解决
报错内容如下 > 6-241.0.0 build > electron-builder • electron-builder version24.13.3 os10.0.22631 • loaded configuration filepackage.json ("build" field) • writing effective config filedist\builder-effective-config.yaml • pack…...

leetcode226反转二叉树
本文主要讲解反转二叉树的要点与细节,按照步骤思考更方便理解 c和java代码如下,末尾 给你一棵二叉树的根节点 root ,翻转这棵二叉树,并返回其根节点。 具体要点: 1. 首先我们要理解题意, 反转二叉树具体…...
【自然语言处理系列】探索NLP:使用Spacy进行分词、分句、词性标注和命名实体识别,并以《傲慢与偏见》与全球恐怖活动两个实例文本进行分析
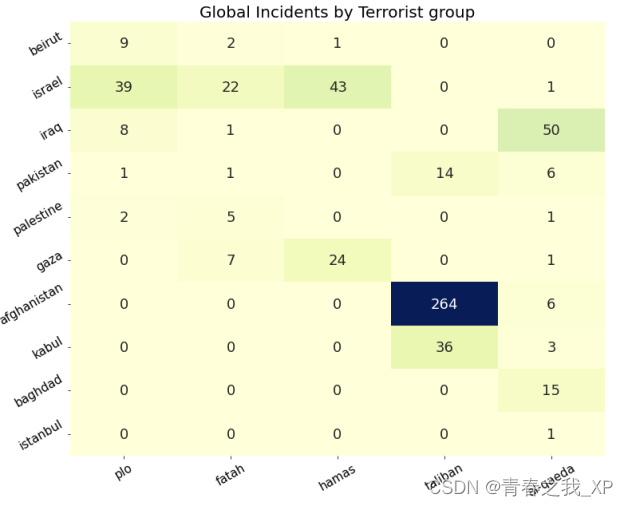
本文深入探讨了scaPy库在文本分析和数据可视化方面的应用。首先,我们通过简单的文本处理任务,如分词和分句,来展示scaPy的基本功能。接着,我们利用scaPy的命名实体识别和词性标注功能,分析了Jane Austen的经典小说《傲…...

【Rust】function和methed的区别
文章目录 functionmethedAssociated Functions 参考资料 一句话总结: function和methed很多都是相同的。 不同点在于: methed定义在结构体里面,并且它的第一个参数肯定是self,代表结构体实例。方法需要用实例名.方法名调用当然结…...

Python:操作 Excel 折叠
💖亲爱的技术爱好者们,热烈欢迎来到 Kant2048 的博客!我是 Thomas Kant,很开心能在CSDN上与你们相遇~💖 本博客的精华专栏: 【自动化测试】 【测试经验】 【人工智能】 【Python】 Python 操作 Excel 系列 读取单元格数据按行写入设置行高和列宽自动调整行高和列宽水平…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的----NTFS源代码分析--重要
根目录0xa0属性对应的Ntfs!_SCB中的FileObject是什么时候被建立的 第一部分: 0: kd> g Breakpoint 9 hit Ntfs!ReadIndexBuffer: f7173886 55 push ebp 0: kd> kc # 00 Ntfs!ReadIndexBuffer 01 Ntfs!FindFirstIndexEntry 02 Ntfs!NtfsUpda…...

从实验室到产业:IndexTTS 在六大核心场景的落地实践
一、内容创作:重构数字内容生产范式 在短视频创作领域,IndexTTS 的语音克隆技术彻底改变了配音流程。B 站 UP 主通过 5 秒参考音频即可克隆出郭老师音色,生成的 “各位吴彦祖们大家好” 语音相似度达 97%,单条视频播放量突破百万…...
