【子串】3. 无重复的最长子串
3. 无重复的最长子串
难度:中等难度
力扣地址:https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/

题目看起来简单,刷起来有好几个坑,特此记录一下,解法比官网的更加简单,可读性强。时间复杂度与空间复杂度与官方一样。
问题描述
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = “abcabcbb”
输出: 3
解释: 因为无重复字符的最长子串是 “abc”,所以其长度为 3。
示例 2:
输入: s = “bbbbb”
输出: 1
解释: 因为无重复字符的最长子串是 “b”,所以其长度为 1。
示例 3:
输入: s = “pwwkew”
输出: 3
解释: 因为无重复字符的最长子串是 “wke”,所以其长度为 3。
请注意,你的答案必须是 子串 的长度,“pwke” 是一个子序列,不是子串。
提示:
- 0 <= s.length <= 5 * 1 0 4 10^4 104;
s由英文字母、数字、符号和空格组成。
问题分析

解决方法
结合示例 1,我做了一个详细的双指针移动 PPT 示意图。


解题代码
请小伙伴们结合上面的PPT进行理解,以下内容包括两种方法,第一种是基于哈希表,第二种使用 vector 替代哈希表,更快更节省资源(时间复杂度不变)
方法一:基于 unordered_map 记录历史 + 双指针一次遍历
class Solution {
public:int lengthOfLongestSubstring(string s) {// 用于记录每个字符最后一次出现的索引unordered_map<char, int> map;// 最终结果int result = 0;// 指针的开始位置,我们最终要求的无重复字符的最长子串的开始位置// 这个指针将会根据实际情况而移动,方向是一直向右int start = 0;// 一次遍历所有字符// 遍历过程中主要处理两个事情// 1. 移动 start 指针// 2. 计算现在已知的最长子串的长度for (int i = 0; i < s.length(); i++) {// 查找历史中该点auto tmp = map.find(s[i]);// 如果历史中存在数据,需要更新 start 的位置,表示新的最长子串的开始位置// 需要注意的是,更新后的start 必须越来越大,即向右边移动,避免 start 向左边移动if (tmp != map.end()) {start = max(tmp -> second + 1, start);}// 更新最后的结果,即最长子串的长度result = max(result, i - start + 1);// 写入/更新 s[i] 字符的索引map[s[i]] = i;}return result;}
};
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( ∑ ) O(\sum) O(∑),其中 ∑ \sum ∑ 表示字符集(即字符串中可以出现的字符),∣ ∑ \sum ∑∣ 表示字符集的大小。在本题中没有明确说明字符集,因此可以默认为所有 ASCII 码在 [0,128) 内的字符,即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符,而字符最多有 ∣ ∑ \sum ∑∣ 个,因此空间复杂度为 O(∣ ∑ \sum ∑∣)。
方法二:基于 vector 记录历史 + 双指针一次遍历
class Solution {
public:int lengthOfLongestSubstring(string s) {// 用于记录每个字符最后一次出现的索引vector<int> lastIndex(256, -1);// 最终结果int result = 0;// 指针的开始位置,我们最终要求的无重复字符的最长子串的开始位置int start = 0;// 一次遍历所有字符for (int end = 0; end < s.length(); end++) {// 更新 start 的位置if (lastIndex[s[end]] != -1) {start = max(lastIndex[s[end]] + 1, start);}// 更新最后的结果,即最长子串的长度result = max(result, end - start + 1);// 更新 s[end] 字符的索引lastIndex[s[end]] = end;}return result;}
};
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( ∑ ) O(\sum) O(∑),其中 ∑ \sum ∑ 表示字符集(即字符串中可以出现的字符),∣ ∑ \sum ∑∣ 表示字符集的大小。在本题中没有明确说明字符集,因此可以默认为所有 ASCII 码在 [0,128) 内的字符,即 ∣Σ∣=128。我们需要用到哈希集合来存储出现过的字符,而字符最多有 ∣ ∑ \sum ∑∣ 个,因此空间复杂度为 O(∣ ∑ \sum ∑∣)。
总结
这道题目通过简单的双指针和哈希表的结合,可以高效地解决字符串中无重复字符的最长子串问题。这种方法的时间复杂度为O(n),因为每个字符在最坏情况下也只会被访问两次(一次作为结束字符,一次作为开始字符)。空间复杂度为O(1),因为哈希表的大小是固定的,最多为256个字符。
也正是基于这个原因,后面我们增加了使用 vector 提到哈希表,可以更加节省资源以及查找历史的时间。
Smileyan
2024.06.29 22:59
相关文章:

【子串】3. 无重复的最长子串
3. 无重复的最长子串 难度:中等难度 力扣地址:https://leetcode.cn/problems/longest-substring-without-repeating-characters/description/ 题目看起来简单,刷起来有好几个坑,特此记录一下,解法比官网的更加简单&…...

Scrapy中爬虫优化技巧分享
scrapy是一个非常有用的python爬虫框架,它可以帮助我们轻松地从不同的网站上获取数据。同时,scrapy也有越来越多的用户在使用它来爬取数据,因此,在使用scrapy的过程中,我们需要考虑如何优化我们的爬虫,以便…...
自然语言处理-BERT处理框架-transformer
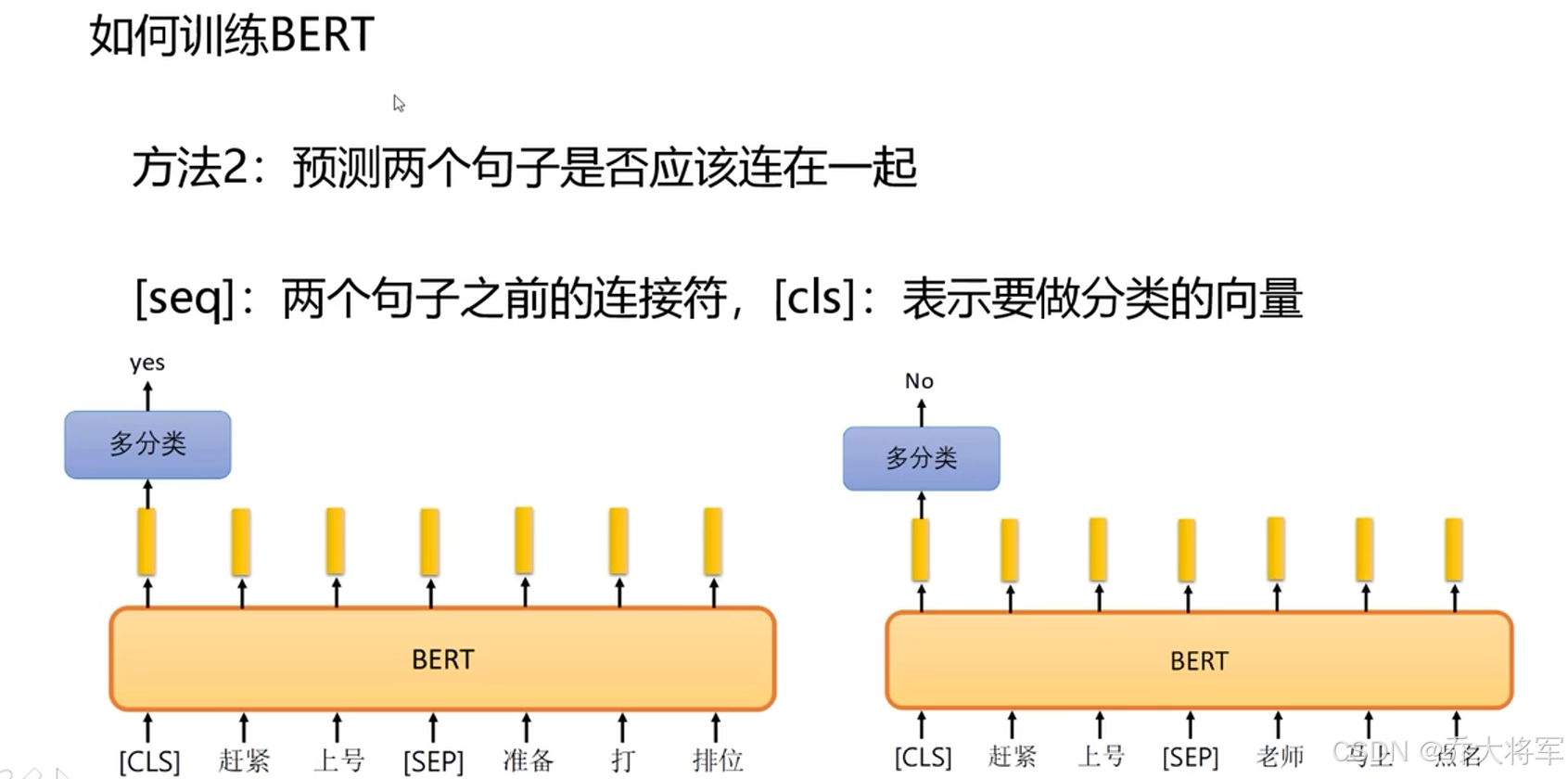
目录 1.介绍 2.Transformer 2.1 引言 2.2 传统RNN网络的问题 2.3 整体架构 2.4 Attention 2.5 Self-Attention如何计算 3.multi-headed机制 4. BERT训练方法 1.介绍 BERT:当前主流的解决框架,一站式搞定NLP任务。(解决一个NLP任务时的考虑…...
)
Kafka~消息系列问题解决:消费顺序问题解决、消息丢失问题优化(不能保证100%)
消息消费顺序问题 使用消息队列的过程中经常有业务场景需要严格保证消息的消费顺序,比如我们同时发了 2 个消息,这 2 个消息对应的操作分别对应的数据库操作是: 用户等级升级。根据用户等级下的订单价格 假如这两条消息的消费顺序不一样造…...

如何确保日常安全运维中的数据加密符合等保2.0标准?
等保2.0标准下的数据加密要求 等保2.0标准是中国信息安全等级保护制度的升级版,它对信息系统的安全保护提出了更为严格的要求。在日常安全运维中,确保数据加密符合等保2.0标准,主要涉及以下几个方面: 数据加密技术的选择ÿ…...

下一代的JDK - GraalVM
GraalVM是最近几年Java相关的新技术领域不多的亮点之一, 被称之为革命性的下一代JDK,那么它究竟有什么神奇之处,又为当前的Java开发带来了一些什么样的改变呢,让我们来详细了解下 下一代的JDK 官网对GraalVM的介绍是 “GraalVM 是…...

Java三方库-单元测试
文章目录 Junit注解常用类无参数单测带参数的单测 Junit 主要版本有4和5版本,注解不太一样, 4迁移5参考官方文档 主要记录下常用的一些操作 其他复杂操作见官网 https://junit.org/junit5/docs/current/user-guide/#overview-java-versions 引入5.9…...

p2p、分布式,区块链笔记: libp2p基础
通信密钥 noise::{Keypair, X25519Spec} X25519/Ed25519类似RSA 算法。Noise 用于设计和实现安全通信协议。它允许通信双方在没有预先共享密钥的情况下进行安全的密钥交换,并通过加密和身份验证保护通信内容。libp2p 提供了对 Noise 协议的原生支持,它允…...

企业本地大模型用Ollama+Open WebUI+Stable Diffusion可视化问答及画图
最近在尝试搭建公司内部用户的大模型,可视化回答,并让它能画图出来, 主要包括四块: Ollama 管理和下载各个模型的工具Open WebUI 友好的对话界面Stable Diffusion 绘图工具Docker 部署在容器里,提高效率以上运行环境Win10, Ollama,SD直接装在windows10下, 然后安装Docker…...

Unity学习笔记---调试
使用Log进行调试 使用Debug.Log方法可以将一些运行时信息打印到Console窗口中。 打印时间戳 //获取时间 Debug.Log(DateTime.Now.ToString());//打印毫秒级的时间 Debug.Log(((DateTime.Now.ToUniversalTime().Ticks - 621355968000000000) / 10000) * 0.001); 打印自定义文…...

Py之dashscope:dashscope的简介、安装和使用方法、案例应用之详细攻略
Py之dashscope:dashscope的简介、安装和使用方法、案例应用之详细攻略 目录 dashscope的简介 1、产品的主要特点和优势包括: dashscope的安装和使用方法 1、安装 2、使用方法 dashscope的案例应用 1、通义千问-Max:通义千问2.5系列 2…...
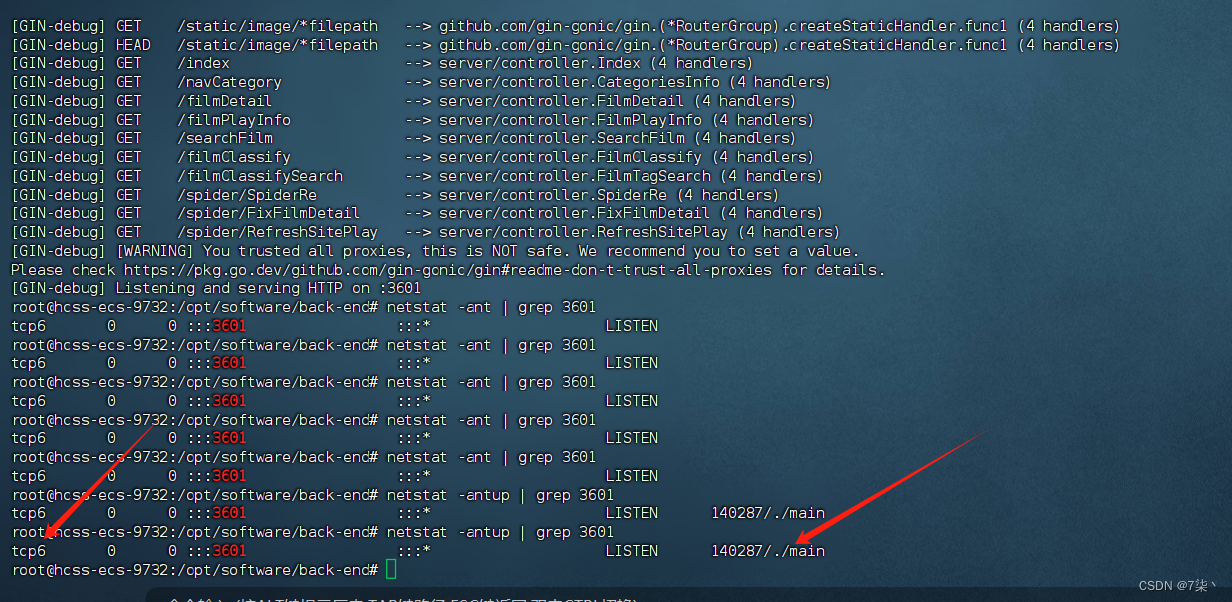
Go使用Gin框架开发的Web程序部署在Linux时,无法绑定监听Ipv4端口
最近有写一部分go语言开发的程序,在部署程序时发现,程序在启动后并没有绑定ipv4的端口,而是直接监听绑定ipv6的端口。 当我用netstat -antup | grep 3601查找我的gin服务启动的端口占用情况的时候发现,我的服务直接绑定了tcp6 &a…...
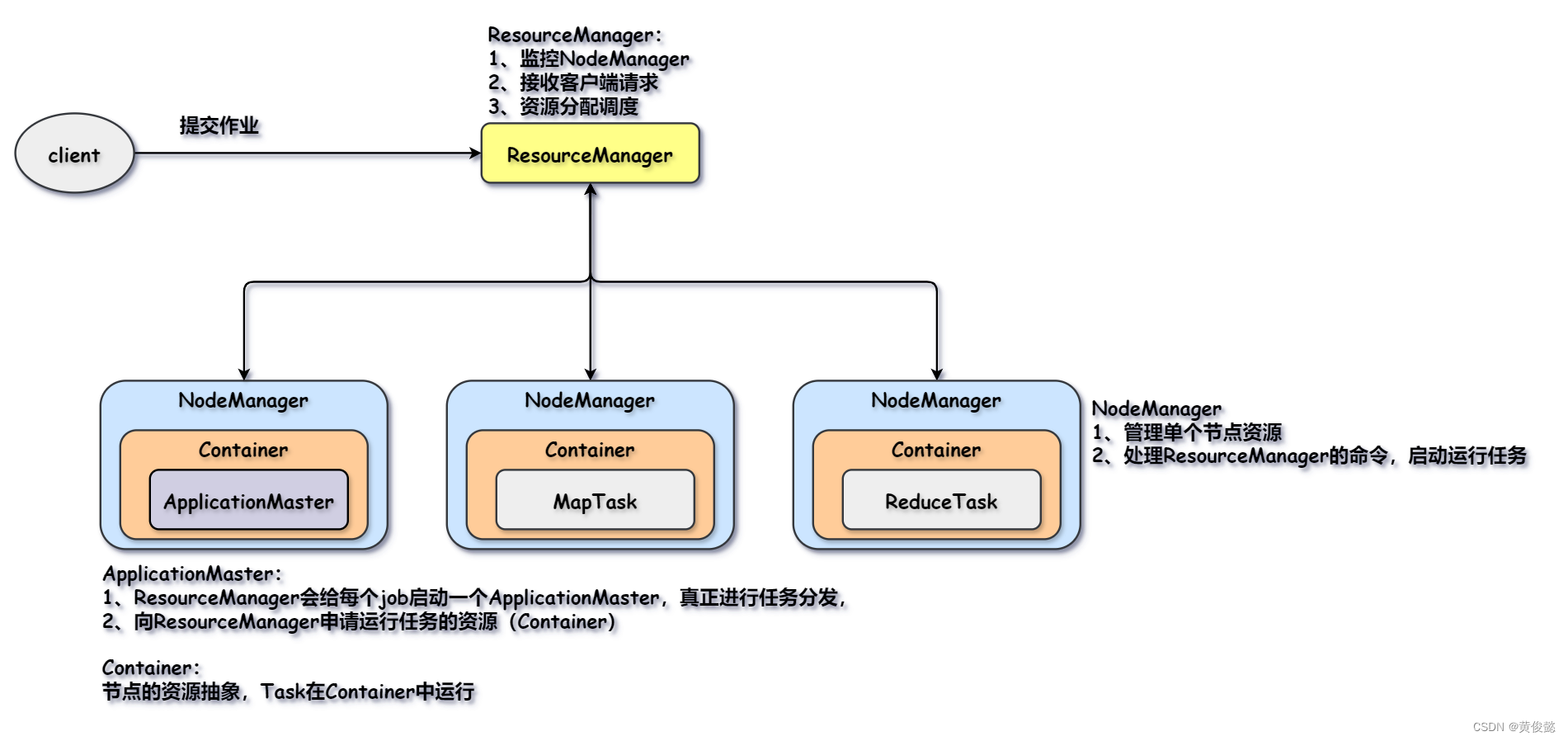
【图解大数据技术】Hadoop、HDFS、MapReduce、Yarn
【图解大数据技术】Hadoop、HDFS、MapReduce、Yarn HadoopHDFSHDFS架构写文件流程读文件流程 MapReduceMapReduce简介MapReduce整体流程 Yarn Hadoop Hadoop是Apache开源的分布式大数据存储与计算框架,由HDFS、MapReduce、Yarn三部分组成。广义上的Hadoop其实是指H…...

AGPT•intelligence:带你领略全新量化交易的风采
随着金融科技的快速发展,量化交易已经成为了投资领域的热门话题。越来越多的投资者开始关注和使用量化交易软件来进行投资决策。在市场上有许多量化交易软件可供选择。 Delaek,是一位资深的金融科技专家,在 2020年成立一家专注于数字资产量化…...

HarmonyOS Next开发学习手册——创建轮播 (Swiper)
Swiper 组件提供滑动轮播显示的能力。Swiper本身是一个容器组件,当设置了多个子组件后,可以对这些子组件进行轮播显示。通常,在一些应用首页显示推荐的内容时,需要用到轮播显示的能力。 针对复杂页面场景,可以使用 Sw…...

【计算机视觉】mmcv库详细介绍
文章目录 MMVC库概览特点和优势主要组件应用案例示例一:数据加载和处理示例二:模型训练和验证MMVC库概览 MMCV 是一个用于计算机视觉研究的开源库,它为各种视觉任务提供了底层的、高度优化的 API。该库涵盖了从数据加载到模型训练的各个方面,广泛应用于开源项目,如 MMDet…...

【面试系列】Go 语言高频面试题
欢迎来到我的博客,很高兴能够在这里和您见面!欢迎订阅相关专栏: ⭐️ 全网最全IT互联网公司面试宝典:收集整理全网各大IT互联网公司技术、项目、HR面试真题. ⭐️ AIGC时代的创新与未来:详细讲解AIGC的概念、核心技术、…...

React 扩展
文章目录 PureComponent1. 使用 React.Component,不会进行浅比较2. 使用 shouldComponentUpdate 生命周期钩子,手动比较3. 使用 React.PureComponent,自动进行浅比较 Render Props1. 使用 Children props(通过组件标签体传入结构&…...

IT入门知识第八部分《云计算》(8/10)
目录 云计算:现代技术的新篇章 1. 云计算基础 1.1 云计算的起源和发展 云计算的早期概念 云计算的发展历程 1.2 云计算的核心特点 按需自助服务 广泛的网络访问 资源池化 快速弹性 按使用量付费 1.3 云计算的优势和挑战 成本效益 灵活性和可扩展性 维…...

Linux-笔记 全志T113移植正点4.3寸RGB屏幕笔记
目录 前言 线序整理 软件 显示调试 触摸调试 背光调试 前言 由于手头有一块4.3寸的RGB屏幕(触摸IC为GT1151),正好开发板上也有40Pin的RGB接口,就想着给移植一下,前期准备工作主要是整理好线序,然后用转接板与杜邦线连接验证好…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...
