算法金 | 协方差、方差、标准差、协方差矩阵

大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」
抱个拳,送个礼
1. 方差
方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在数据分析和机器学习中,方差常用于描述数据集的变异情况
1.1 定义与计算方法 方差的计算方法如下:
- 计算数据集的均值(平均值)
- 计算每个数据点与均值的差值
- 将这些差值平方
- 将平方后的差值相加
- 将总和除以数据点的数量
方差的公式为:
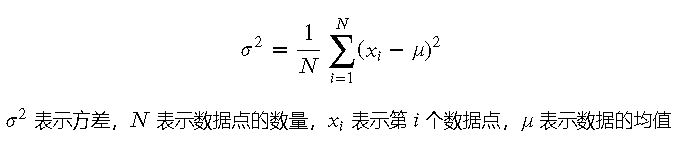
1.2 实际应用 方差在许多领域都有广泛应用。例如,在金融领域,方差用来衡量投资回报率的波动性。在质量控制中,方差用来衡量生产过程的稳定性。在机器学习中,方差用于评估模型的性能和稳定性
1.3 示例
假设我们有一组数据:[1, 2, 3, 4, 5]
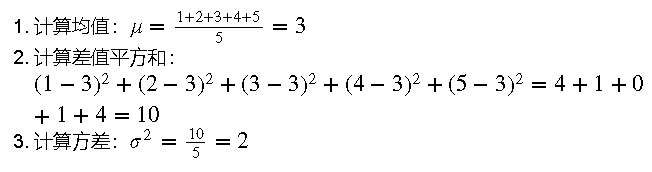
2. 标准差
标准差是方差的平方根,是另一种度量数据分散程度的指标。标准差与方差一样,反映了数据点与均值之间的偏离程度,但标准差的单位与数据本身一致,因此更容易解释和理解
2.1 定义与计算方法 标准差的计算方法如下:
- 计算数据集的均值(平均值)
- 计算每个数据点与均值的差值
- 将这些差值平方
- 将平方后的差值相加
- 将总和除以数据点的数量,得到方差
- 对方差取平方根,得到标准差
标准差的公式为:

2.2 实际应用 标准差广泛应用于各种领域。例如,在金融领域,标准差用来衡量投资回报率的波动性。在质量控制中,标准差用来衡量生产过程的稳定性。在统计分析和数据科学中,标准差用来描述数据集的离散程度
2.3 示例
继续前面的例子,假设我们有一组数据:[1, 2, 3, 4, 5]
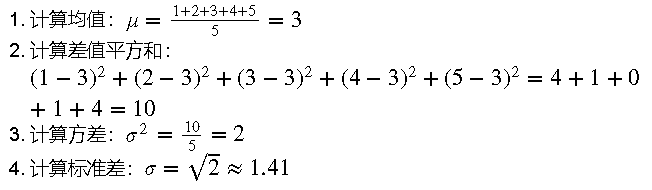
防失联,进免费知识星球,直达算法金 AI 实验室 https://t.zsxq.com/ckSu3
更多内容,见免费知识星球
3. 协方差
协方差是用来衡量两个变量之间关系的一种统计指标。它表示了两个变量如何一起变化:当一个变量变大时,另一个变量是否也变大(正协方差)或变小(负协方差)。协方差的值可以是正、负或零,具体取决于变量之间的关系
3.1 定义与计算方法 协方差的计算方法如下:
- 计算每个变量的均值(平均值)
- 计算每个变量与其均值的差值
- 将两个变量的差值乘积求和
- 将和除以数据点的数量
协方差的公式为:
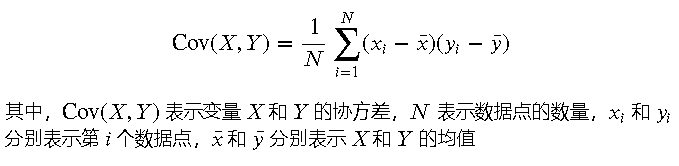
3.2 实际应用 协方差在许多领域都有广泛应用。例如,在金融领域,协方差用来衡量不同资产回报率之间的相关性。在经济学中,协方差用来分析不同经济指标之间的关系。在机器学习中,协方差用于特征选择和数据预处理
3.3 示例
假设我们有两个变量的数据集:𝑋=[1,2,3,4,5]𝑋=[1,2,3,4,5] 和 𝑌=[2,4,6,8,10]
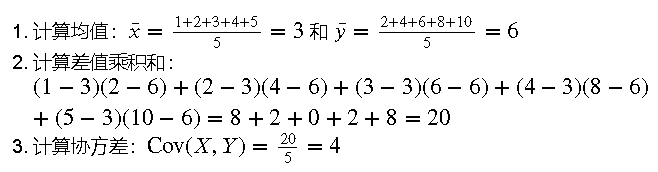
抱个拳,送个礼
点击 ↑ 领取
4. 协方差矩阵
协方差矩阵是用于描述多个变量之间协方差关系的矩阵。它是一个对称矩阵,其中每个元素表示对应变量对之间的协方差。协方差矩阵在多变量统计分析和机器学习中起着重要作用
4.1 定义与计算方法 协方差矩阵的计算方法如下:
- 计算每个变量的均值(平均值)
- 计算每个变量与其均值的差值
- 计算每对变量之间的协方差
- 将协方差填入矩阵对应位置
协方差矩阵的公式为:
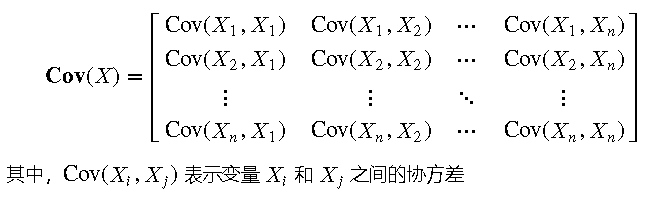
4.2 实际应用 协方差矩阵在数据分析和机器学习中有广泛的应用。例如,在主成分分析(PCA)中,协方差矩阵用于特征降维。在多变量回归分析中,协方差矩阵用于估计回归系数的标准误。在组合投资中,协方差矩阵用于分析不同资产的风险
4.3 示例
假设我们有三个变量的数据集:𝑋1=[1,2,3],𝑋2=[4,5,6],𝑋3=[7,8,9]
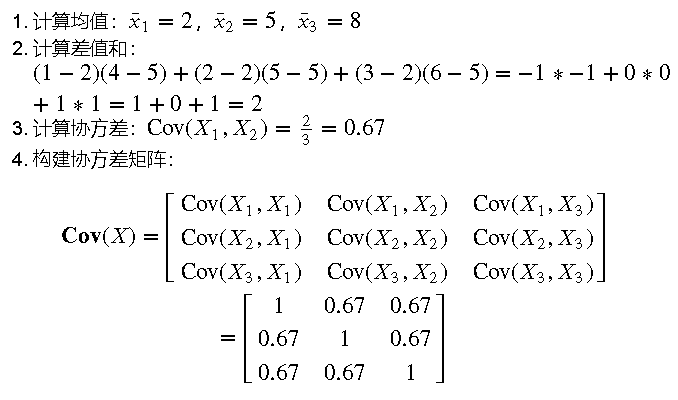
防失联,进免费知识星球,直达算法金 AI 实验室
https://t.zsxq.com/ckSu3
5. 各指标之间的关系与对比
在数据分析和统计学中,方差、标准差、协方差及协方差矩阵都是衡量数据分布和变量关系的重要工具。理解它们之间的关系和区别有助于更好地应用这些工具进行分析
5.1 方差与标准差 方差和标准差都是度量数据分散程度的指标,但它们的单位和解释不同
- 方差:方差表示数据点与均值之间的平方差的平均值,单位是数据单位的平方。方差公式为:
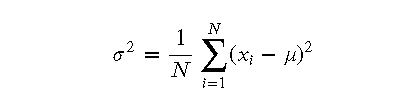
- 标准差:标准差是方差的平方根,因此其单位与数据本身一致。标准差公式为:
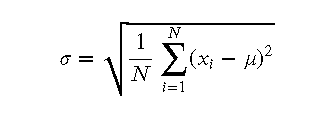
5.2 标准差与协方差 标准差和协方差虽然都是度量数据分布和关系的指标,但它们用于不同的情景
- 标准差:标准差用于度量单个变量的分散程度,是方差的平方根。它可以帮助我们理解单个变量的波动性
- 协方差:协方差用于度量两个变量之间的关系,表示一个变量变化时另一个变量的变化情况。协方差公式为:
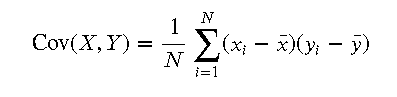
5.3 协方差与协方差矩阵 协方差和协方差矩阵都是用来描述变量之间关系的工具,但协方差矩阵可以同时描述多个变量之间的关系
- 协方差:协方差只描述两个变量之间的关系,正值表示正相关,负值表示负相关
- 协方差矩阵:协方差矩阵是一个对称矩阵,包含多个变量之间的协方差信息,用于多变量统计分析。协方差矩阵公式为:
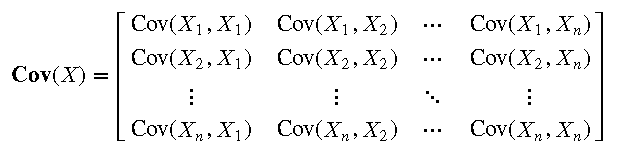
[ 抱个拳,总个结 ]
- 科研为国分忧,创新与民造福 -

日更时间紧任务急,难免有疏漏之处,还请大侠海涵 内容仅供学习交流之用,部分素材来自网络,侵联删
[ 算法金,碎碎念 ]
入选 CSDN 算法领域
内容榜单 Top 1
真香~
全网同名,日更万日,让更多人享受智能乐趣
如果觉得内容有价值,烦请大侠多多 分享、在看、点赞,助力算法金又猛又持久、很黄很 BL 的日更下去;同时邀请大侠 关注、星标 算法金,围观日更万日,助你功力大增、笑傲江湖
相关文章:

算法金 | 协方差、方差、标准差、协方差矩阵
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 1. 方差 方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在…...
FastAPI教程II
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial Cookie参数 定义Cookie参数与定义Query和Path参数一样。 具体步骤如下: 导入Cookie:from fastapi import Cookie声明Cookie参数,声明Cookie参数的方式与声明Query和Path参数…...

Facebook的投流技巧有哪些?
相信大家都知道Facebook拥有着巨大的用户群体和高转化率,在国外社交推广中的影响不言而喻。但随着Facebook广告的竞争越来越激烈,在Facebook广告上获得高投资回报率也变得越来越困难。IPIDEA代理IP今天就教大家如何在Facebook上投放广告的技巧࿰…...

Spring Boot 中的微服务监控与管理
微服务的概述 微服务架构的优点和挑战 优点: 灵活性和可扩展性:微服务架构允许每个服务单独部署和扩展,这使得系统可以更灵活地适应不同的业务需求和负载变化。 使团队更加聚焦:每个微服务都有明确的职责,这使得开发团队可以更加聚焦,专注于开发他们的服务。 技术和框…...
模拟卷)
【计算机网络】期末复习(1)模拟卷
一、选择题 1. 电路交换的三个阶段是建立连接、()和释放连接 A. Hello包探测 B. 通信 C. 二次握手 D. 总线连接 2. 一下哪个协议不属于C/S模式() A. SNMP…...

【软件工程中的演化模型及其优缺点】
文章目录 1. 增量模型什么是增量模型?优点缺点 2. 增量-迭代模型什么是增量-迭代模型?优点缺点 3. 螺旋模型什么是螺旋模型?优点缺点 1. 增量模型 什么是增量模型? 增量模型是一种逐步增加功能和特性的开发方法。项目被划分为多…...

Oracle 数据库详解:概念、结构、使用场景与常用命令
1. 引言 Oracle 数据库作为全球领先的关系型数据库管理系统(RDBMS),在企业级应用中占据了重要地位。本文将详细介绍Oracle数据库的核心概念、架构、常用操作及其广泛的使用场景,旨在为读者提供全面而深入的理解。 2. Oracle 数据…...

FreeRTOS的裁剪与移植
文章目录 1 FreeRTOS裁剪与移植1.1 FreeRTOS基础1.1.1 RTOS与GPOS1.1.2 堆与栈1.1.3 FreeRTOS核心文件1.1.4 FreeRTOS语法 1.2 FreeRTOS移植和裁剪 1 FreeRTOS裁剪与移植 1.1 FreeRTOS基础 1.1.1 RTOS与GPOS 实时操作系统(RTOS):是指当…...

能求一个数字的字符数量的程序
目录 开头程序程序的流程图程序输入与打印的效果例1输入输出 例2输入输出 关于这个程序的一些实用内容结尾 开头 大家好,我叫这是我58,今天,我们先来看一下下面的程序。 程序 #define _CRT_SECURE_NO_WARNINGS 1 #include <stdio.h>…...
PTA-线性表实验(JAVA)
题目1:Josephus环的问题及算法 【实验内容】 编程实现如下功能: 题意说明:古代某法官要判决n个犯人的死刑,他有一条荒唐的法律,将犯人站成一个圆圈,从第start个犯人开始数起,每数到第distance的…...

LeetCode:494. 目标和
题目 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添…...

HarmonyOS Next开发学习手册——选项卡 (Tabs)
当页面信息较多时,为了让用户能够聚焦于当前显示的内容,需要对页面内容进行分类,提高页面空间利用率。 Tabs 组件可以在一个页面内快速实现视图内容的切换,一方面提升查找信息的效率,另一方面精简用户单次获取到的信息…...

LeetCode2710.移除字符串中的尾随零
cpp class Solution { public:string removeTrailingZeros(string num) {int flag 0;string s num;int size num.length();for (int i num.length() - 1; i > 0; i--) {if (num[i] ! 0)break;if (num[i] 0) {size--;}}s.resize(size);return s;} };...
PPT录屏怎么录?PPT录屏,3种方法简单操作
在数字化时代,PPT已经成为我们日常工作、学习和生活中不可或缺的一部分。无论是商务报告、教学课件还是产品展示,PPT都能帮助我们更加生动、直观地传递信息。然而,有时候我们会面临PPT录屏怎么录的问题。这时,一个好的PPT录屏功能…...

HarmonyOS开发:应用完整性校验
简介 为了确保应用的完整性和来源可靠,OpenHarmony需要对应用进行签名和验签。 应用开发阶段: 开发者完成开发并生成安装包后,需要开发者对安装包进行签名,以证明安装包发布到设备的过程中没有被篡改。OpenHarmony的应用完整性校…...

【MySQL基础篇】SQL指令:DQL及DCL
1、DQL DQL - 介绍 DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据表中的记录。(在MySQL中应用是最为广泛的) 查询关键字:SELECT DQL - 语法 SELECT 字段列表 FROM 表名列表 WHER…...
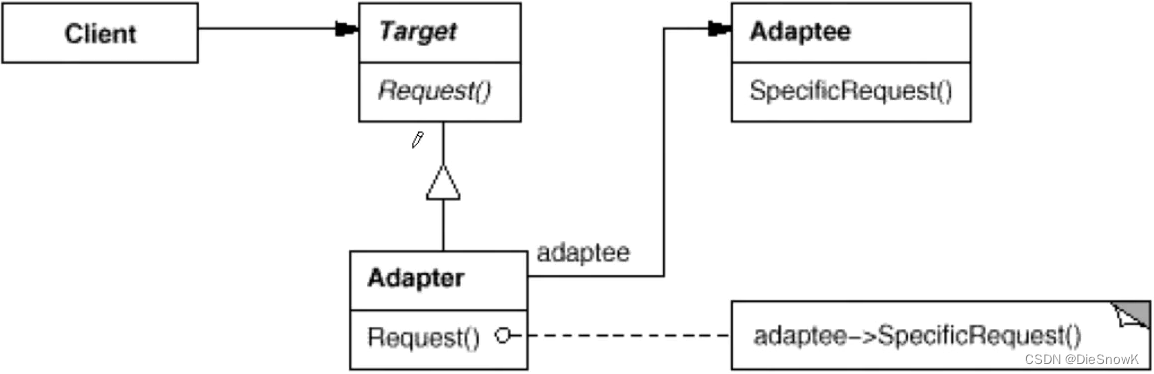
[C++][设计模式][适配器模式]详细讲解
目录 1.动机2.模式定义3.要点总结4.代码感受 1.动机 在软件系统中,由于应用环境的变化,常常需要将”一些现存的对象“放在新的环境中应用,但是新环境要求的接口是这些现存对象所不满足如何应对这些”迁移的变化“?如何既能利用现…...

8080时序驱动TFT显示屏 驱动IC GC9307
8080时序总共有控制线 CS片选线 DC(命令数据控制线) RD读控制线 WR写控制线 和N条数据线。 控制底层代码如下; 写读代码,读的代码反过来就行 inline void TFT8080WriteDat(unsigned char dat) {CS_L;//开始片选DC_H;//写数据 // RD_H;//禁止读WR_H;//禁止写WR_L;//写入…...

K8S 集群节点缩容
环境说明: 主机名IP地址CPU/内存角色K8S版本Docker版本k8s231192.168.99.2312C4Gmaster1.23.1720.10.24k8s232192.168.99.2322C4Gwoker1.23.1720.10.24k8s233(需下线)192.168.99.2332C4Gwoker1.23.1720.10.24 1. K8S 集群节点缩容 当集群中有…...

Web-HTML-事件
1 需求 2 语法 3 示例 4 参考资料 HTML 事件 | 菜鸟教程...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

练习(含atoi的模拟实现,自定义类型等练习)
一、结构体大小的计算及位段 (结构体大小计算及位段 详解请看:自定义类型:结构体进阶-CSDN博客) 1.在32位系统环境,编译选项为4字节对齐,那么sizeof(A)和sizeof(B)是多少? #pragma pack(4)st…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

基于Springboot+Vue的办公管理系统
角色: 管理员、员工 技术: 后端: SpringBoot, Vue2, MySQL, Mybatis-Plus 前端: Vue2, Element-UI, Axios, Echarts, Vue-Router 核心功能: 该办公管理系统是一个综合性的企业内部管理平台,旨在提升企业运营效率和员工管理水…...

永磁同步电机无速度算法--基于卡尔曼滤波器的滑模观测器
一、原理介绍 传统滑模观测器采用如下结构: 传统SMO中LPF会带来相位延迟和幅值衰减,并且需要额外的相位补偿。 采用扩展卡尔曼滤波器代替常用低通滤波器(LPF),可以去除高次谐波,并且不用相位补偿就可以获得一个误差较小的转子位…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...

算法打卡第18天
从中序与后序遍历序列构造二叉树 (力扣106题) 给定两个整数数组 inorder 和 postorder ,其中 inorder 是二叉树的中序遍历, postorder 是同一棵树的后序遍历,请你构造并返回这颗 二叉树 。 示例 1: 输入:inorder [9,3,15,20,7…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
