LeetCode:494. 目标和
题目
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 ‘+’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 :
例如,nums = [2, 1] ,可以在 2 之前添加 ‘+’ ,在 1 之前添加 ‘-’ ,然后串联起来得到表达式 “+2-1” 。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
示例 1:
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1
输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
思路
方法一:使用递归
方法二:使用动态规划,记数组的元素和为 sum,添加 - 号的元素之和为 a,则其余添加 + 的元素之和为 sum−a,得到的表达式的结果为(sum-a)-a = sum - 2a = target , res != -1检查memo数组是否已缓存了该子问题的解。如果有直接返回,c < nums[i]表示当前元素值大于负载值,无法选择当前元素。直接递归处理下一元素,如果negatives无法选择当前元素,考虑两种选择: 1,不选择当前元素,递归处理下一元素dfs(dfs, i-1, c) 。 2,选择当前元素,负载减去该元素值,递归dfs(dfs, i-1, c-nums[i]),则两种选择的方案数相加就是包含和不包含当前元素的总方案数。
代码
方法一
class Solution {
public:int count = 0;int findTargetSumWays(vector<int>& nums, int target) {backtrack(nums, target, 0, 0);return count;}void backtrack(vector<int>& nums, int target, int index, int sum) {if (index == nums.size()) {if (sum == target) {count++;}} else {backtrack(nums, target, index + 1, sum + nums[index]);backtrack(nums, target, index + 1, sum - nums[index]);}}
};方法二
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int s = reduce(nums.begin(), nums.end(), 0) - abs(target);if (s < 0 || s % 2)return 0;int m = s / 2;int n = nums.size();vector<vector<int>> memo(n, vector<int>(m + 1, -1));auto dfs = [&](auto&& dfs, int i, int c) -> int {if (i < 0)return c == 0;int& res = memo[i][c];if (res != -1)return res;if (c < nums[i]) {return res = dfs(dfs, i - 1, c);}return res = dfs(dfs, i - 1, c) + dfs(dfs, i - 1, c - nums[i]);};return dfs(dfs, n - 1, m);}
};
总结
- 使用回溯可以遍历不同的方案,
- 问题转化成在数组 nums 中选取若干元素,使得这些元素之和等于 ’ - ’ 次数,计算选取元素的方案数,就可以使用动态规划了
相关文章:

LeetCode:494. 目标和
题目 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添…...

HarmonyOS Next开发学习手册——选项卡 (Tabs)
当页面信息较多时,为了让用户能够聚焦于当前显示的内容,需要对页面内容进行分类,提高页面空间利用率。 Tabs 组件可以在一个页面内快速实现视图内容的切换,一方面提升查找信息的效率,另一方面精简用户单次获取到的信息…...

LeetCode2710.移除字符串中的尾随零
cpp class Solution { public:string removeTrailingZeros(string num) {int flag 0;string s num;int size num.length();for (int i num.length() - 1; i > 0; i--) {if (num[i] ! 0)break;if (num[i] 0) {size--;}}s.resize(size);return s;} };...
PPT录屏怎么录?PPT录屏,3种方法简单操作
在数字化时代,PPT已经成为我们日常工作、学习和生活中不可或缺的一部分。无论是商务报告、教学课件还是产品展示,PPT都能帮助我们更加生动、直观地传递信息。然而,有时候我们会面临PPT录屏怎么录的问题。这时,一个好的PPT录屏功能…...

HarmonyOS开发:应用完整性校验
简介 为了确保应用的完整性和来源可靠,OpenHarmony需要对应用进行签名和验签。 应用开发阶段: 开发者完成开发并生成安装包后,需要开发者对安装包进行签名,以证明安装包发布到设备的过程中没有被篡改。OpenHarmony的应用完整性校…...

【MySQL基础篇】SQL指令:DQL及DCL
1、DQL DQL - 介绍 DQL英文全称是Data Query Language(数据查询语言),数据查询语言,用来查询数据表中的记录。(在MySQL中应用是最为广泛的) 查询关键字:SELECT DQL - 语法 SELECT 字段列表 FROM 表名列表 WHER…...
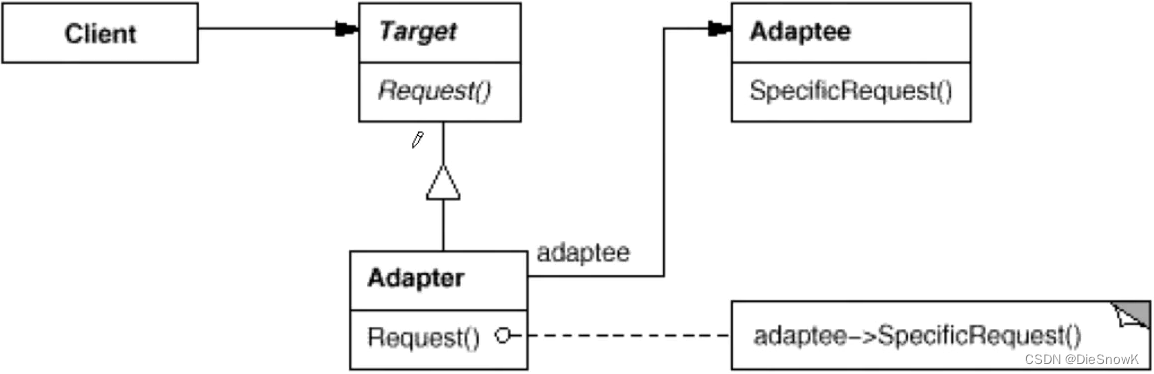
[C++][设计模式][适配器模式]详细讲解
目录 1.动机2.模式定义3.要点总结4.代码感受 1.动机 在软件系统中,由于应用环境的变化,常常需要将”一些现存的对象“放在新的环境中应用,但是新环境要求的接口是这些现存对象所不满足如何应对这些”迁移的变化“?如何既能利用现…...

8080时序驱动TFT显示屏 驱动IC GC9307
8080时序总共有控制线 CS片选线 DC(命令数据控制线) RD读控制线 WR写控制线 和N条数据线。 控制底层代码如下; 写读代码,读的代码反过来就行 inline void TFT8080WriteDat(unsigned char dat) {CS_L;//开始片选DC_H;//写数据 // RD_H;//禁止读WR_H;//禁止写WR_L;//写入…...

K8S 集群节点缩容
环境说明: 主机名IP地址CPU/内存角色K8S版本Docker版本k8s231192.168.99.2312C4Gmaster1.23.1720.10.24k8s232192.168.99.2322C4Gwoker1.23.1720.10.24k8s233(需下线)192.168.99.2332C4Gwoker1.23.1720.10.24 1. K8S 集群节点缩容 当集群中有…...

Web-HTML-事件
1 需求 2 语法 3 示例 4 参考资料 HTML 事件 | 菜鸟教程...
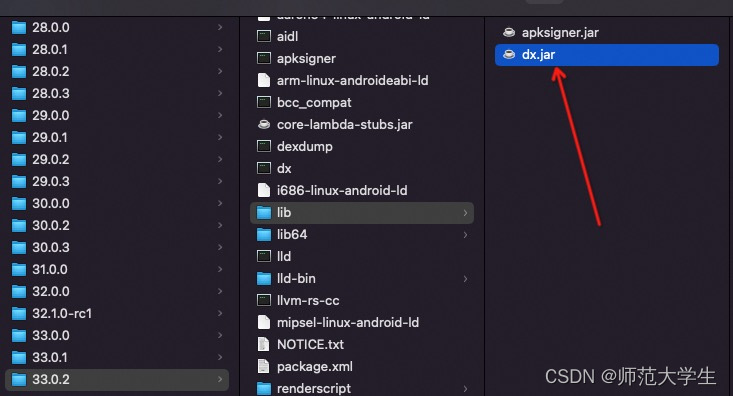
Installed Build Tools revision xxx is corrupted. Remove and install again 解决
1.在buildTools文件下找到对应的sdk版本,首先将版本对应目录下的d8.bat改名为dx.bat。 2.在lib文件下将d8.jar改名为dx.jar。 3.重新编译工程即可...

AI 与 Python 实战干货:基于深度学习的图像识别
《AI 与 Python 实战干货:基于深度学习的图像识别》 今天咱不啰嗦,直接上干货! 在 AI 领域,特别是图像识别方面,Python 简直是一把利器。咱就以手写数字识别为例,来看看怎么用 Python 实现一个深度学习模…...

万字长文详解数据结构:树 | 第6章 | Java版大话数据结构 | 二叉树 | 哈夫曼树 | 二叉树遍历 | 构造二叉树 | LeetCode练习
📌本篇分享的大话数据结构中🎄树🎄这一章的知识点,在此基础上,增加了练习题帮助大家理解一些重要的概念✅;同时,由于原文使用的C语言代码,不利于学习Java语言的同学实践,…...
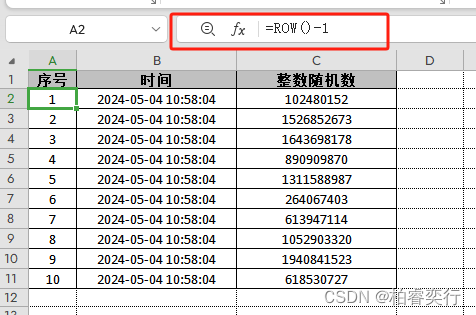
NPOI入门指南:轻松操作Excel文件的.NET库
目录 引言 一、NPOI概述 二、NPOI的主要用途 三、安装NPOI库 四、NPOI基本使用 六、性能优化和内存管理 七、常见问题与解决方案 八、结论 附录 引言 Excel文件作为数据处理的重要工具,广泛应用于各种场景。然而,在没有安装Microsoft Office的…...
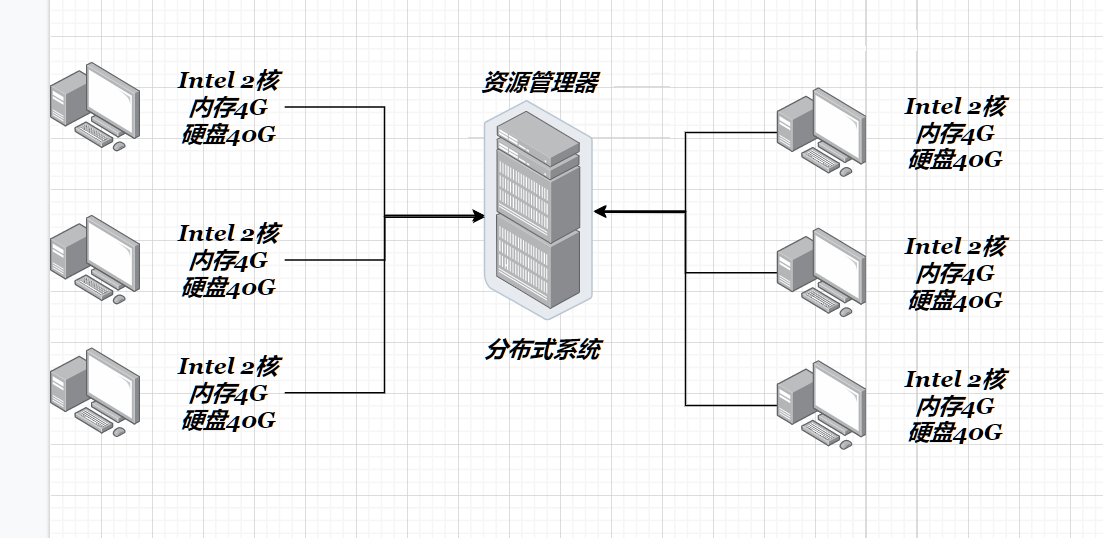
【高性能服务器】服务器概述
🔥博客主页: 我要成为C领域大神🎥系列专栏:【C核心编程】 【计算机网络】 【Linux编程】 【操作系统】 ❤️感谢大家点赞👍收藏⭐评论✍️ 本博客致力于知识分享,与更多的人进行学习交流 服务器概述 服…...

003 SSM框架整合
文章目录 整合web.xmlapplicationContext-dao.xmlapplicationContext-service.xmlspringmvc.xmldb.propertieslog4j.propertiespom.xml 测试sqlItemController.javaItemMapper.javaItem.javaItemExample.javaItemService.javaItemServiceImpl.javaItemMapper.xml 整合 将工程的…...
web刷题记录(7)
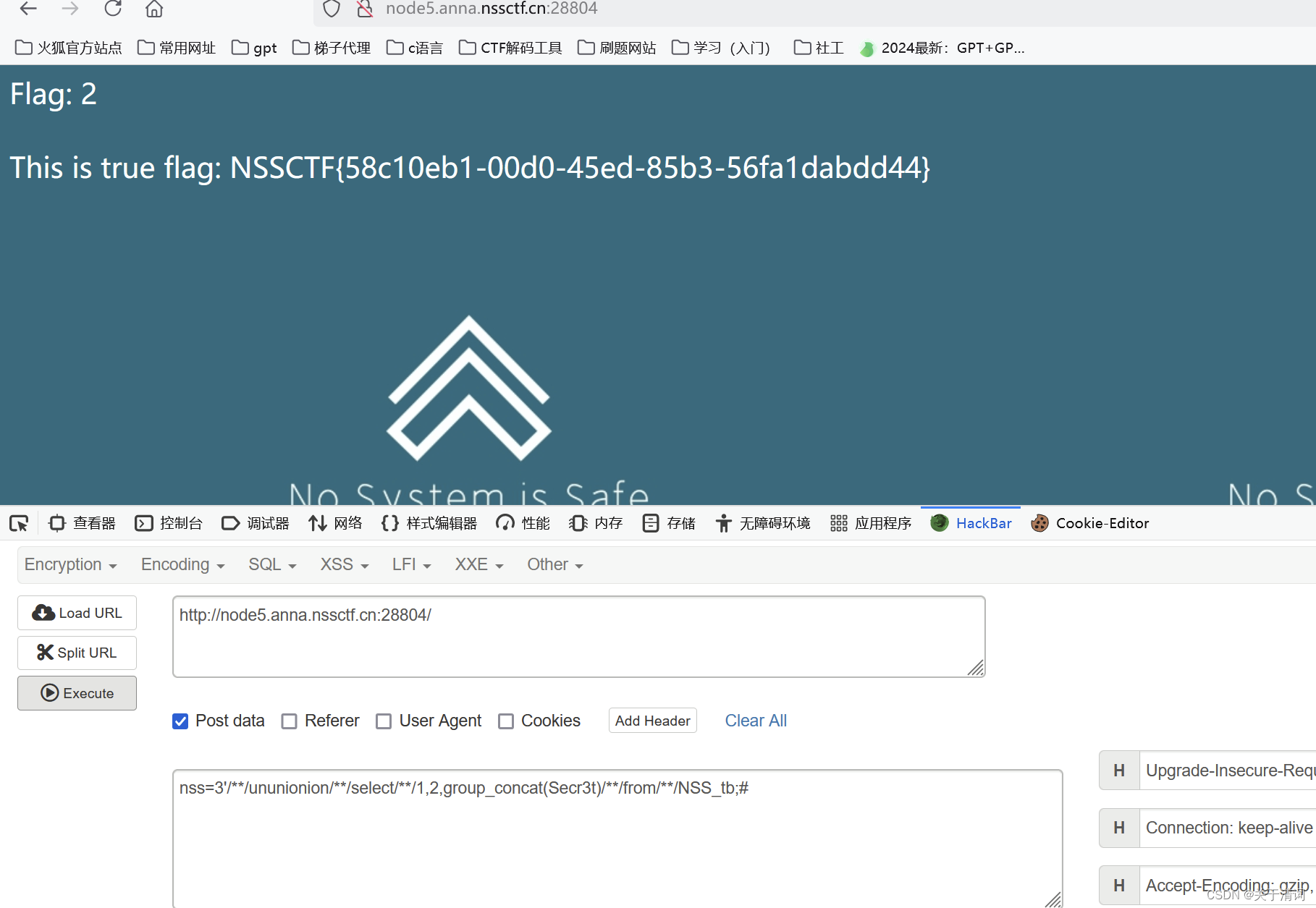
[HDCTF 2023]SearchMaster 打开环境,首先的提示信息就是告诉我们,可以用post传参的方式来传入参数data 首先考虑的还是rce,但是这里发现,不管输入那种命令,它都会直接显示在中间的那一小行里面,而实际的命令…...
【单片机毕业设计选题24037】-基于STM32的电力系统电力参数无线监控系统
系统功能: 系统上电后,OLED显示“欢迎使用电力监控系统请稍后”,两秒后显示“Waiting..”等待ESP8266初始化完成, ESP8266初始化成功后进入正常页面显示, 第一行显示电压值(单位V) 第二行显示电流值&am…...

Python使用彩虹表来尝试对MD5哈希进行破解
MD5是一种散列算法,它是不可逆的,无法直接解密。它的主要作用是将输入数据进行散列,生成一个固定长度的唯一哈希值。 然而,可以使用预先计算好的MD5哈希值的彩虹表(Rainbow Table)来尝试对MD5进行破解。彩…...
数据恢复篇: 如何在数据丢失后恢复照片
数据丢失的情况并不少见。如果您曾经遇到过图像丢失的情况,您可能想过照片恢复工具是如何工作的?可能会丢失多少数据图像?即使是断电也可能导致照片和媒体文件丢失。 话虽如此,如果你认为删除的照片无法恢复,那你就错…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

全球首个30米分辨率湿地数据集(2000—2022)
数据简介 今天我们分享的数据是全球30米分辨率湿地数据集,包含8种湿地亚类,该数据以0.5X0.5的瓦片存储,我们整理了所有属于中国的瓦片名称与其对应省份,方便大家研究使用。 该数据集作为全球首个30米分辨率、覆盖2000–2022年时间…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...

MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析
Java求职者面试指南:Spring、Spring Boot、Spring MVC与MyBatis技术解析 一、第一轮基础概念问题 1. Spring框架的核心容器是什么?它的作用是什么? Spring框架的核心容器是IoC(控制反转)容器。它的主要作用是管理对…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...

向量几何的二元性:叉乘模长与内积投影的深层联系
在数学与物理的空间世界中,向量运算构成了理解几何结构的基石。叉乘(外积)与点积(内积)作为向量代数的两大支柱,表面上呈现出截然不同的几何意义与代数形式,却在深层次上揭示了向量间相互作用的…...
