[leetcode hot 150]第五百三十题,二叉搜索树的最小绝对差
题目:
给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。
差值是一个正数,其数值等于两值之差的绝对值。
解析:
minDiffInBST方法是主要方法。- 创建一个
ArrayList来存储树的节点值。inorderTraversal方法进行中序遍历,将节点值添加到列表中。- 在得到有序列表后,遍历列表,计算相邻元素的差值。
- 使用
Math.min来持续更新最小差值。- 最后,返回找到的最小差值。
import java.util.ArrayList;
import java.util.List;public class no_530 {public static void main(String[] args) {TreeNode root = new TreeNode(4);root.left = new TreeNode(2);root.right = new TreeNode(6);root.left.left = new TreeNode(1);root.left.right = new TreeNode(3);System.out.println(getMinimumDifference(root));}public static int getMinimumDifference(TreeNode root) {List<Integer> values = new ArrayList<>();inorderTraversal(root, values);int minDiff = Integer.MAX_VALUE;for (int i = 1; i < values.size(); i++) {minDiff = Math.min(minDiff, values.get(i) - values.get(i - 1));}return minDiff;}public static void inorderTraversal(TreeNode node, List<Integer> values) {if (node == null) return;inorderTraversal(node.left, values);values.add(node.val);inorderTraversal(node.right, values);}
}
相关文章:

[leetcode hot 150]第五百三十题,二叉搜索树的最小绝对差
题目: 给你一个二叉搜索树的根节点 root ,返回 树中任意两不同节点值之间的最小差值 。 差值是一个正数,其数值等于两值之差的绝对值。 解析: minDiffInBST 方法是主要方法。创建一个 ArrayList 来存储树的节点值。inorderTrave…...

【Docker】可视化平台Portainer
文章目录 Portainer的特点Portainer的安装步骤注意事项 Docker的可视化工具Portainer是一个轻量级的容器管理平台,它为用户提供了一个直观的图形界面来管理Docker环境。以下是关于Portainer的详细介绍和安装步骤: Portainer的特点 轻量级:P…...

MySQL高级-MVCC-原理分析(RR级别)
文章目录 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView2、总结 1、RR隔离级别下,仅在事务中第一次执行快照读时生成ReadView,后续复用该ReadView 而RR 是可重复读,在一个事务中&…...

压力测试Monkey命令参数和报告分析
目录 常用参数 -p <测试的包名列表> -v 显示日志详细程度 -s 伪随机数生成器的种子值 --throttle < 毫秒> --ignore-crashes 忽略崩溃 --ignore-timeouts 忽略超时 --monitor-native-crashes 监视本地崩溃代码 --ignore-security-exceptions 忽略安全异常 …...
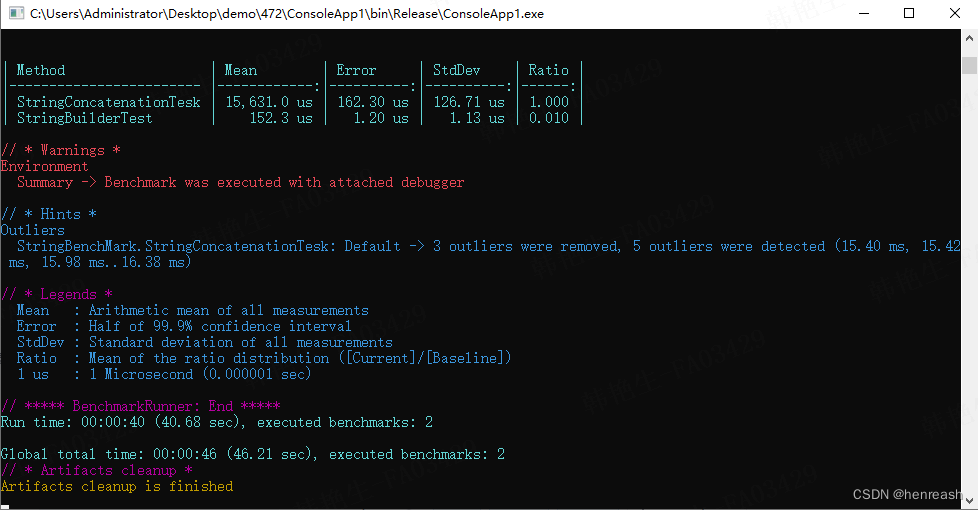
C# Benchmark
创建控制台项目(或修改现有项目的Main方法代码),Nget导入Benchmark0.13.12,创建测试类: public class StringBenchMark{int[] numbers;public StringBenchMark() {numbers Enumerable.Range(1, 20000).ToArray();}[Be…...
算法金 | 协方差、方差、标准差、协方差矩阵
大侠幸会,在下全网同名「算法金」 0 基础转 AI 上岸,多个算法赛 Top 「日更万日,让更多人享受智能乐趣」 抱个拳,送个礼 1. 方差 方差是统计学中用来度量一组数据分散程度的重要指标。它反映了数据点与其均值之间的偏离程度。在…...
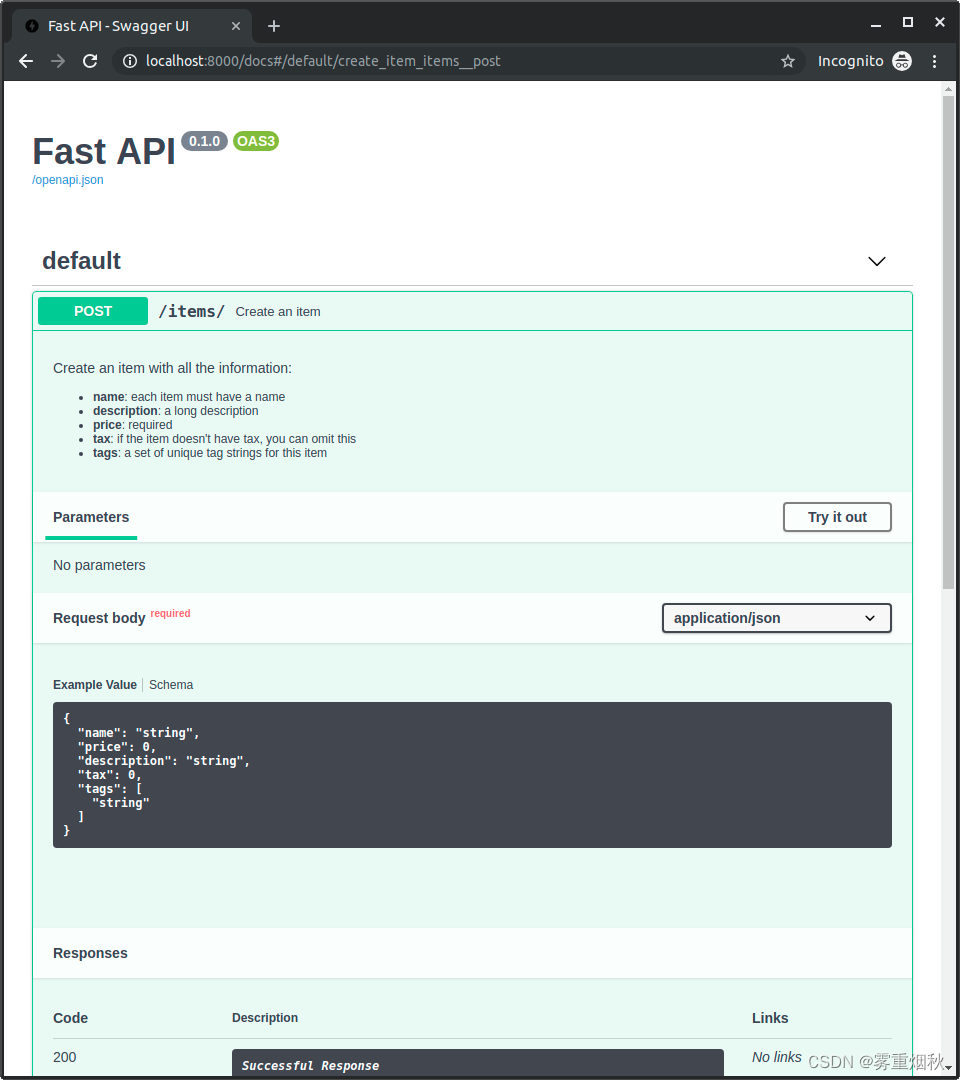
FastAPI教程II
本文参考FastAPI教程https://fastapi.tiangolo.com/zh/tutorial Cookie参数 定义Cookie参数与定义Query和Path参数一样。 具体步骤如下: 导入Cookie:from fastapi import Cookie声明Cookie参数,声明Cookie参数的方式与声明Query和Path参数…...

Facebook的投流技巧有哪些?
相信大家都知道Facebook拥有着巨大的用户群体和高转化率,在国外社交推广中的影响不言而喻。但随着Facebook广告的竞争越来越激烈,在Facebook广告上获得高投资回报率也变得越来越困难。IPIDEA代理IP今天就教大家如何在Facebook上投放广告的技巧࿰…...

Spring Boot 中的微服务监控与管理
微服务的概述 微服务架构的优点和挑战 优点: 灵活性和可扩展性:微服务架构允许每个服务单独部署和扩展,这使得系统可以更灵活地适应不同的业务需求和负载变化。 使团队更加聚焦:每个微服务都有明确的职责,这使得开发团队可以更加聚焦,专注于开发他们的服务。 技术和框…...
模拟卷)
【计算机网络】期末复习(1)模拟卷
一、选择题 1. 电路交换的三个阶段是建立连接、()和释放连接 A. Hello包探测 B. 通信 C. 二次握手 D. 总线连接 2. 一下哪个协议不属于C/S模式() A. SNMP…...

【软件工程中的演化模型及其优缺点】
文章目录 1. 增量模型什么是增量模型?优点缺点 2. 增量-迭代模型什么是增量-迭代模型?优点缺点 3. 螺旋模型什么是螺旋模型?优点缺点 1. 增量模型 什么是增量模型? 增量模型是一种逐步增加功能和特性的开发方法。项目被划分为多…...

Oracle 数据库详解:概念、结构、使用场景与常用命令
1. 引言 Oracle 数据库作为全球领先的关系型数据库管理系统(RDBMS),在企业级应用中占据了重要地位。本文将详细介绍Oracle数据库的核心概念、架构、常用操作及其广泛的使用场景,旨在为读者提供全面而深入的理解。 2. Oracle 数据…...

FreeRTOS的裁剪与移植
文章目录 1 FreeRTOS裁剪与移植1.1 FreeRTOS基础1.1.1 RTOS与GPOS1.1.2 堆与栈1.1.3 FreeRTOS核心文件1.1.4 FreeRTOS语法 1.2 FreeRTOS移植和裁剪 1 FreeRTOS裁剪与移植 1.1 FreeRTOS基础 1.1.1 RTOS与GPOS 实时操作系统(RTOS):是指当…...

能求一个数字的字符数量的程序
目录 开头程序程序的流程图程序输入与打印的效果例1输入输出 例2输入输出 关于这个程序的一些实用内容结尾 开头 大家好,我叫这是我58,今天,我们先来看一下下面的程序。 程序 #define _CRT_SECURE_NO_WARNINGS 1 #include <stdio.h>…...
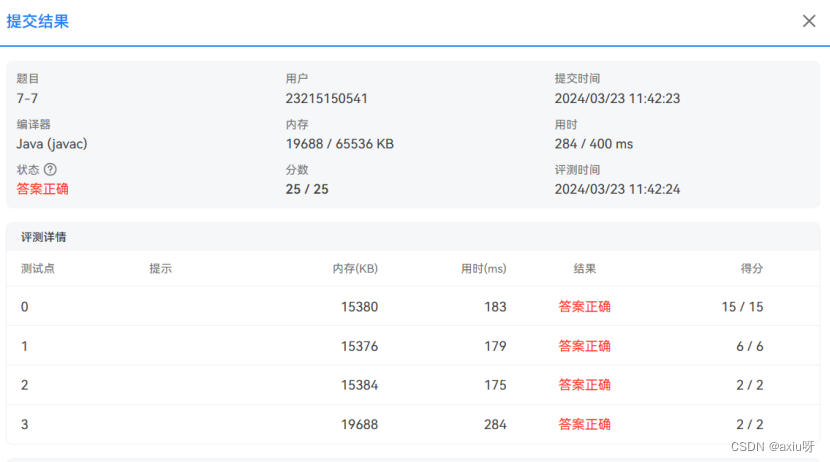
PTA-线性表实验(JAVA)
题目1:Josephus环的问题及算法 【实验内容】 编程实现如下功能: 题意说明:古代某法官要判决n个犯人的死刑,他有一条荒唐的法律,将犯人站成一个圆圈,从第start个犯人开始数起,每数到第distance的…...

LeetCode:494. 目标和
题目 给你一个非负整数数组 nums 和一个整数 target 。 向数组中的每个整数前添加 ‘’ 或 ‘-’ ,然后串联起所有整数,可以构造一个 表达式 : 例如,nums [2, 1] ,可以在 2 之前添加 ‘’ ,在 1 之前添…...

HarmonyOS Next开发学习手册——选项卡 (Tabs)
当页面信息较多时,为了让用户能够聚焦于当前显示的内容,需要对页面内容进行分类,提高页面空间利用率。 Tabs 组件可以在一个页面内快速实现视图内容的切换,一方面提升查找信息的效率,另一方面精简用户单次获取到的信息…...

LeetCode2710.移除字符串中的尾随零
cpp class Solution { public:string removeTrailingZeros(string num) {int flag 0;string s num;int size num.length();for (int i num.length() - 1; i > 0; i--) {if (num[i] ! 0)break;if (num[i] 0) {size--;}}s.resize(size);return s;} };...
PPT录屏怎么录?PPT录屏,3种方法简单操作
在数字化时代,PPT已经成为我们日常工作、学习和生活中不可或缺的一部分。无论是商务报告、教学课件还是产品展示,PPT都能帮助我们更加生动、直观地传递信息。然而,有时候我们会面临PPT录屏怎么录的问题。这时,一个好的PPT录屏功能…...

HarmonyOS开发:应用完整性校验
简介 为了确保应用的完整性和来源可靠,OpenHarmony需要对应用进行签名和验签。 应用开发阶段: 开发者完成开发并生成安装包后,需要开发者对安装包进行签名,以证明安装包发布到设备的过程中没有被篡改。OpenHarmony的应用完整性校…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...
