【牛客】牛客小白月赛97 题解 A - E
文章目录
- A - 三角形
- B - 好数组
- C - 前缀平方和序列
- D - 走一个大整数迷宫
- E - 前缀和前缀最大值
A - 三角形
map存一下每个数出现了多少次,再遍历map
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;map<int, int> mp;for (int i = 0; i < n; i ++ ){int x; cin >> x;mp[x] ++ ;}for (auto t : mp){if (t.second >= 3){cout << "YES\n";return;}}cout << "NO\n";return;
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;
// cin >> t;while (t--){solve();}
}
B - 好数组
数组没有 0 就是好数组
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;vector<int> a(n + 1);for (int i = 1; i <= n; i ++ ) cin >> a[i];for (int i = 1; i <= n; i ++ ){if (a[i] == 0){cout << "NO\n";return;}}cout << "YES\n";
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
C - 前缀平方和序列
对 x 开方,得到的就是能存在数组里的所有数的个数,我们要取 n 个,也就是 C(sqrt(x), n)
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;int Jc[maxn + 1];void calJc() //求 maxn 以内的数的阶乘 不知道开多少就1e6吧爆不了
{Jc[0] = Jc[1] = 1;for(int i = 2; i < maxn; i++) Jc[i] = Jc[i - 1] * i % mod;
}int pow(int a, int n, int p) // 快速幂取模
{int ans = 1;while (n){if (n & 1) ans = ans * a % p;a = a * a % p;n >>= 1;}return ans;
}int niYuan(int a, int b) //费马小定理求逆元
{return pow(a, b - 2, b);
}int C(int a, int b) // 组合数
{if(a < b) return 0;return Jc[a] * niYuan(Jc[b], mod) % mod * niYuan(Jc[a - b], mod) % mod;
}void solve()
{calJc();int n, x;cin >> n >> x;int cnt = sqrt(x);int ans = C(cnt, n);cout << ans << '\n';
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
D - 走一个大整数迷宫
首先需要注意到 c 的值和 b 一点关系都没有,因为 b 不可能对 (p - 1) 有任何贡献
明确这一点之后只需要 bfs 就可以了,注意需要判断 st[x][y][k] 不重复,(x, y) 就是点坐标,k 就是到达该点的余数
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 1e5 + 10;
const int maxn = 1e6 + 10;
const int mod = 1e9 + 7;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;int dx[4] = {0, 0, 1, -1}, dy[4] = {1, -1, 0, 0};struct node {int dist, res, x, y;
};void solve()
{int n, m, p;cin >> n >> m >> p;vector<vector<int>> a(n + 1, vector<int>(m + 1)), b(n + 1, vector<int>(m + 1));for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )cin >> a[i][j];for (int i = 1; i <= n; i ++ )for (int j = 1; j <= m; j ++ )cin >> b[i][j];int ans = INF;queue<struct node> q;q.push({0, a[1][1] % (p - 1), 1, 1});vector<vector<vector<bool>>> st(n + 1, vector<vector<bool>>(m + 1, vector<bool>(p + 1)));while (q.size()){auto t = q.front();q.pop();if (st[t.x][t.y][t.res]) continue;st[t.x][t.y][t.res] = true;if (t.x == n && t.y == m && t.res % (p - 1) == 0){cout << t.dist << '\n';return;}if (t.dist >= 1e6){cout << -1 << '\n';return;}for (int i = 0; i < 4; i ++ ){int nx = t.x + dx[i], ny = t.y + dy[i];if (nx <= 0 || nx > n || ny <= 0 || ny > m) continue;q.push({t.dist + 1, (t.res + a[nx][ny]) % (p - 1), nx, ny});}}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
E - 前缀和前缀最大值
a 的前缀最大值数量最多的情况就是把正数全都排在前面的时候,此时数量为 正数个数+1,加的 1 代表最前面的前缀和 0
数量最少的情况就是把负数全都排在正数前面,且正数从小到大排列,这种情况怎么计算呢,因为 b 的值域最大只有100,所以用 cnt_pos[i][j] 表示前 i 个元素中 j 出现的次数,之后计算最多需要多少个正数可以把负数都抵消即可
答案就是最大值-最小值+1
#include <bits/stdc++.h>using namespace std;#define int long long
using i64 = long long;typedef pair<int, int> PII;
typedef pair<int, char> PIC;
typedef pair<double, double> PDD;
typedef pair<int, PII> PIII;
typedef pair<int, pair<int, bool>> PIIB;const int N = 10;
const int maxn = 1e6 + 10;
const int mod = 998244353;
const int mod1 = 954169327;
const int mod2 = 906097321;
const int INF = 0x3f3f3f3f3f3f3f3f;void solve()
{int n;cin >> n;vector<int> a(n + 1), pre_neg(n + 1);vector<vector<int>> cnt_pos(n + 1, vector<int>(110));for (int i = 1; i <= n; i ++ ){cin >> a[i];pre_neg[i] = pre_neg[i - 1] - min(a[i], (i64)0);for (int j = 1; j <= 100; j ++ ){cnt_pos[i][j] = cnt_pos[i - 1][j] + (a[i] == j);}} int q;cin >> q;while (q -- ){int l, r;cin >> l >> r;int cnt_plus = 0; // 正数个数for (int i = 1; i <= 100; i ++ ) cnt_plus += cnt_pos[r][i] - cnt_pos[l - 1][i];int sum_tmp = 0; // 当前正数之和int cnt_need = 0; // 需要多少正数和负数抵消for (int i = 1; i <= 100; i ++ ){int cnt = cnt_pos[r][i] - cnt_pos[l - 1][i];if (sum_tmp + i * cnt >= (pre_neg[r] - pre_neg[l - 1])){cnt_need += (pre_neg[r] - pre_neg[l - 1] - sum_tmp) / i;break;}else{cnt_need += cnt;sum_tmp += cnt * i;}}cout << cnt_plus + 1 - (cnt_plus - cnt_need + 1) + 1 << '\n';}
}signed main()
{ios::sync_with_stdio(false);cin.tie(0), cout.tie(0);int t = 1;// cin >> t;while (t--){solve();}
}
相关文章:

【牛客】牛客小白月赛97 题解 A - E
文章目录 A - 三角形B - 好数组C - 前缀平方和序列D - 走一个大整数迷宫E - 前缀和前缀最大值 A - 三角形 map存一下每个数出现了多少次,再遍历map #include <bits/stdc.h>using namespace std;#define int long long using i64 long long;typedef pair<…...

Spring Boot中泛型参数的灵活运用:最佳实践与性能优化
泛型是Java中一种强大的特性,它提供了编写通用代码的能力,使得代码更加灵活和可复用。在Spring Boot应用程序中,泛型参数的灵活运用可以带来诸多好处,包括增强代码的可读性、提高系统的健壮性以及优化系统的性能。本文将深入探讨在…...

MySQL建表时的注意事项
以下是我对MySQL建表时的注意事项。其实,建表事项有很多,我的总结如下: 1 存储引擎的选择,一般做开发,都是要支持事务的,所以选择InnoDB 2 对字段类型的选择: 对于日期类型如果要记录时分…...
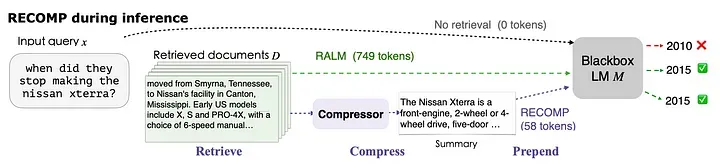
Advanced RAG 09:『提示词压缩』技术综述
编者按: 如何最大限度地发挥 LLMs 的强大能力,同时还能控制其推理成本?这是当前业界研究的一个热点课题。 针对这一问题,本期精心选取了一篇关于"提示词压缩"(Prompt Compression)技术的综述文章。正如作者所说…...
DroneCAN 适配器节点(二))
(13)DroneCAN 适配器节点(二)
文章目录 前言 2 固件 2.1 基于F103 2.2 基于F303 2.3 基于F431 3 ArduPilot固件DroneCAN设置 3.1 f303-通用设置示例 4 DroneCAN适配器节点 前言 这些节点允许现有的 ArduPilot 支持的外围设备作为 DroneCAN 或 MSP 设备适应 CAN 总线。这也允许扩展自动驾驶仪硬件的…...
摸鱼大数据——Spark基础——Spark环境安装——Spark Local[*]搭建
一、虚拟机配置 查看每一台的虚拟机的IP地址和网关地址 查看路径: cat /etc/sysconfig/network-scripts/ifcfg-ens33 2.修改 VMware的网络地址: 使用VMnet8 3.修改windows的对应VMware的网卡地址 4.通过finalshell 或者其他的shell连接工具即可连接使用即可, 连接后, 测试一…...
)
函数内部结构分层浅析(从MVC分层架构联想)
函数内部结构分层浅析(从MVC分层架构联想) 分层架构:一种将软件代码按不同功能进行划分的架构模式。 优点包括: 可维护性:各层职责明确,易于单独修改维护。 可扩展性:方便添加或修改某一层,不…...

【three.js案例二】时空隧道
import * as THREE from ./build/three.module.js // 引入轨道控制器扩展库OrbitControls.js import { OrbitControls } from three/addons/controls/OrbitControls.js; // 引入dat.gui.js的一个类GUI import { GUI } from three/addons/libs/lil-gui.module.min.js;// 场景 co…...

动手学深度学习(Pytorch版)代码实践 -计算机视觉-48全连接卷积神经网络(FCN)
48全连接卷积神经网络(FCN) 1.构造函数 import torch import torchvision from torch import nn from torch.nn import functional as F import matplotlib.pyplot as plt import liliPytorch as lp from d2l import torch as d2l# 构造模型 pretrained…...

【Python游戏】猫和老鼠
本文收录于 《一起学Python趣味编程》专栏,从零基础开始,分享一些Python编程知识,欢迎关注,谢谢! 文章目录 一、前言二、代码示例三、知识点梳理四、总结一、前言 本文介绍如何使用Python的海龟画图工具turtle,开发猫和老鼠游戏。 什么是Python? Python是由荷兰人吉多范…...

【无标题】c# WEBAPI 读写表到Redis
//c# WEBAPI 读写表到Redis using System; using System.Collections.Generic; using System.Linq; using System.Net; using System.Net.Http; using System.Web.Http; using Newtonsoft.Json; using StackExchange.Redis; using System.Data; using System.Web; namespace …...
)
【剑指Offer系列】53-0到n中缺失的数字(index)
给定一个包含 [0, n] 中 n 个数的数组 nums ,找出 [0, n] 这个范围内没有出现在数组中的那个数。 示例 1: 输入:nums [3,0,1] 输出:2 解释:n 3,因为有 3 个数字,所以所有的数字都在范围 [0,3]…...

docker compose部署zabbix7.0官方方法快速搭建
环境介绍: 系统:centos7 官方文档:https://www.zabbix.com/documentation/current/zh/manual/installation/containers docker镜像加速 vi /etc/docker/daemon.json{"registry-mirrors": ["https://docker.1panel.live&quo…...
?)
分库分表之后如何设计主键ID(分布式ID)?
文章目录 1、数据库的自增序列步长方案2、分表键结合自增序列3、UUID4、雪花算法5、redis的incr方案总结 在进行数据库的分库分表操作后,必然要面临的一个问题就是主键id如何生成,一定是需要一个全局的id来支持,所以分库分表之后,…...
秋招突击——6/28、6.29——复习{数位DP——度的数量}——新作{}
文章目录 引言复习数位DP——度的数量个人实现参考实现 总结 引言 头一次产生了那么强烈的动摇,对于未来没有任何的感觉的,不知道将会往哪里走,不知道怎么办。可能还是因为实习吧,再加上最近复习也没有什么进展,并不知…...

Spring Boot中使用Thymeleaf进行页面渲染
Spring Boot中使用Thymeleaf进行页面渲染 大家好,我是免费搭建查券返利机器人省钱赚佣金就用微赚淘客系统3.0的小编,也是冬天不穿秋裤,天冷也要风度的程序猿!今天我们将探讨如何在Spring Boot应用中使用Thymeleaf模板引擎进行页面…...

恢复策略(下)-事务故障后的数据库恢复、系统故障后的数据库恢复(检查点技术)、介质故障后的数据库恢复
一、数据库恢复-事务故障 系统通过对事物进行UNDO操作和REDO操作可实现故障后的数据库状态恢复 1、对于发生事务故障后的数据库恢复 恢复机制在不影响其他事务运行的情况下,强行回滚夭折事务,对该事务进行UNDO操作,来撤销该事务已对数据库…...

如何知道docker谁占用的显卡的显存?
文章目录 python环境安装nvidia-htop查看pid加一个追踪总结一下【找到容器创建时间】使用说明示例 再总结一下【用PID找到容器创建时间,从而找到谁创建的】使用说明示例 python环境安装nvidia-htop nvidia-htop是一个看详细的工具。 pip3 install nvidia-htop查看…...
wps linux node.js 加载项开发,和离线部署方案
环境准备 windwos 安装node.js 安装VSCode 安装wps linux 安装node.js 安装VSCode 安装wps 通过npm 安装wpsjs SDK 使用npm安装wpsjs npm install -g wpsjs 创建一个项目 wpsjs create WPS-Addin-PPT 创建项目会让你选择2个东西: 1:选择你的文…...
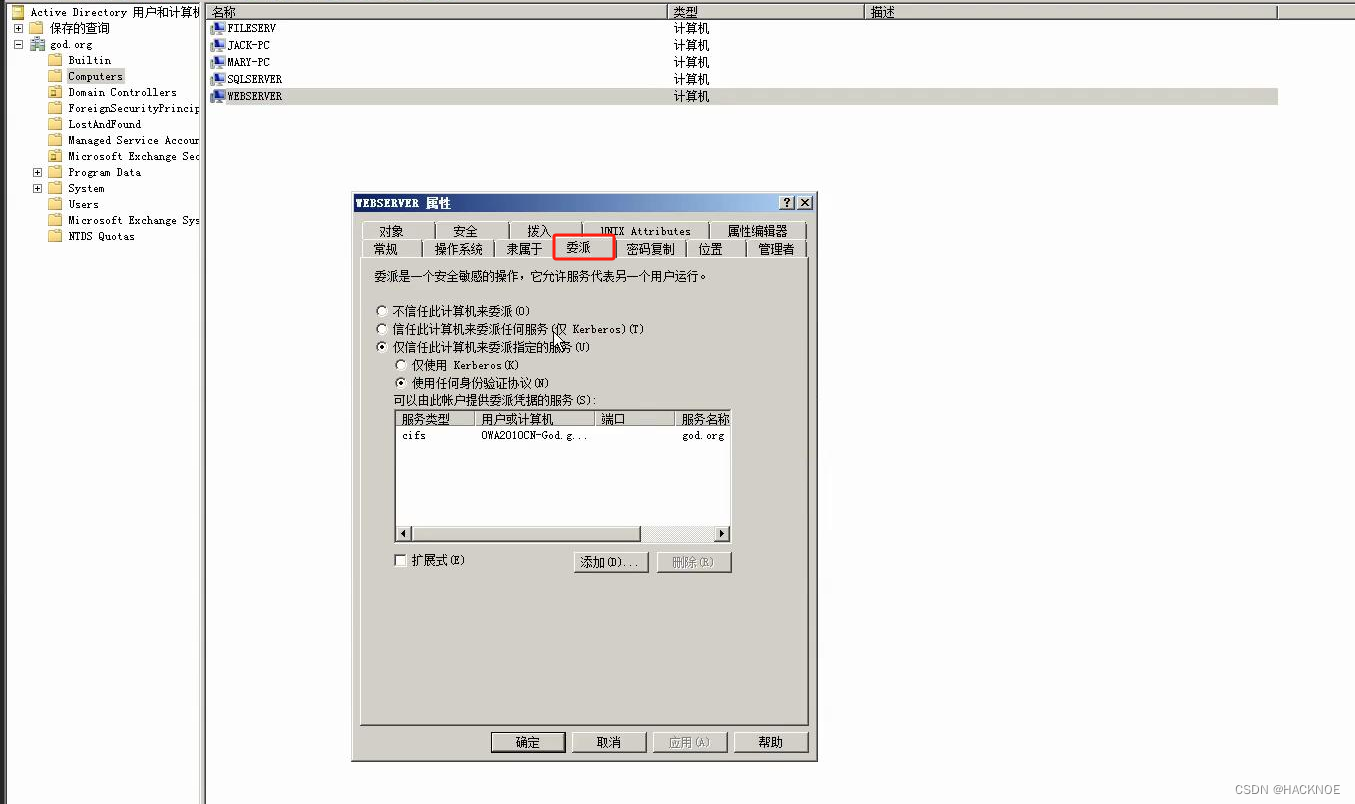
红队内网攻防渗透:内网渗透之内网对抗:横向移动篇Kerberos委派安全非约束系约束系RBCD资源系Spooler利用
红队内网攻防渗透 1. 内网横向移动1.1 委派安全知识点1.1.1 域委派分类1.1.2 非约束委派1.1.2.1 利用场景1.1.2.2 复现配置:1.1.2.3 利用思路1:诱使域管理员访问机器1.1.2.3.1 利用过程:主动通讯1.1.2.3.2 利用过程:钓鱼1.1.2.4 利用思路2:强制结合打印机漏洞1.1.2.5 利用…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

【配置 YOLOX 用于按目录分类的图片数据集】
现在的图标点选越来越多,如何一步解决,采用 YOLOX 目标检测模式则可以轻松解决 要在 YOLOX 中使用按目录分类的图片数据集(每个目录代表一个类别,目录下是该类别的所有图片),你需要进行以下配置步骤&#x…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

C++ 设计模式 《小明的奶茶加料风波》
👨🎓 模式名称:装饰器模式(Decorator Pattern) 👦 小明最近上线了校园奶茶配送功能,业务火爆,大家都在加料: 有的同学要加波霸 🟤,有的要加椰果…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
